高轨GNSS信号可用性分析

卢克文，王新龙*，申亮亮，蔡远文，陈 鼎

(1.北京航空航天大学 宇航学院，北京 100083；2.北京控制与电子技术研究所，北京 100038；3.航天工程大学 研究生院，北京 101416；4.天地一体化信息技术国家重点实验室，北京 100086)

0 引 言

全球卫星导航系统(Global Navigation Satellite System，GNSS)具有全球、全天候、实时性强和定位精度高的特点，这是其他导航系统所不能比拟的[1]。为了最大限度地发掘GNSS的潜力并使导航卫星资源得到充分的利用，GNSS的服务范围逐渐从陆地域扩大到空间域[2]。目前，利用GNSS对中、低轨卫星定位的技术较为成熟[3]，并已部分应用于工程。基于GNSS的高轨卫星定位技术仍存在很多问题。GNSS卫星的发射天线朝向地球，且主瓣信号的波束角有限[4]，而高轨卫星的轨道高度通常高于GNSS星座，故高轨卫星仅能接收地球另一面的导航信号。由于地球的遮挡和自由空间传播损耗的增加，高轨环境中GNSS信号的品质较差，导致GNSS卫星可见性较差。此外，GNSS信号的高动态特性会对信号的捕获、跟踪产生不良影响，影响GNSS信号的可用性。同时，高轨环境中可见星较少且几何构型较差，导航系统的几何精度因子(Geometric Dilution of Precision，GDOP)较大。因此，目前基于GNSS的高轨卫星定位技术仍处于探索阶段[5]。

国内外已有多例高轨卫星星载GNSS接收机飞行试验验证了基于GNSS的高轨卫星定位技术的可行性。20世纪末，国外机构进行飞行试验验证了高于GPS星座的地球同步轨道卫星可跟踪GPS主瓣和旁瓣信号[6]。2001年，NASA发射AMSAT-OSCAR-40卫星，对HEO/GEO轨道卫星利用GPS导航进行了探测性试验[7-8]。2014年，中国月球探测器嫦娥5T1在50 000 km左右的高度成功完成了GNSS信号在轨测试[9]。2016年，在中国海南文昌发射的实践十七号卫星搭载了可兼容GPS/BDS /GLONASS系统主瓣和旁瓣导航信号的高灵敏度GNSS接收机，用于开展地球同步轨道GNSS在轨自主导航试验验证[10]。

国外学者率先开始进行有关高轨GNSS信号可用性的研究工作。文献[11]研究了应用于高轨航天器自主导航的GPS接收机结构，并从可见星数目、信号载噪比、多普勒频移和几何精度因子等方面对高轨环境GNSS信号特性进行了初步分析。文献[12]对GPS卫星空间导航服务域(Space Service Volume，SSV)的特性进行了初步评估，评估结果显示了北斗三代(BDS III)与GPS，GLONASS和伽利略的组合对月球探测航天器在近地段轨道的导航具有潜在的应用价值。目前国内也有较多有关高轨GNSS信号可用性的研究工作。文献[1]分别考虑了单GNSS系统和多GNSS系统组合时的情况，从卫星可见性、动态性和几何精度因子等方面探究了信号的可用性。文献[3]从GNSS卫星可见性和信号强度两方面分析了信号的可用性，提出了多系统互操作组合定位方法，并给出了多系统数据融合算法来解决GNSS进行高轨飞行器定位的相关问题。文献[13]以GPS接收机指标设计为目标，结合空间几何模型和信号链路传播的特点，从接收机处理时间、可用星数、接收机接收功率等方面探究了GPS信号的可用性，工程指导性较强。文献[14]分析了GNSS卫星可见性，并探究了不同轨道高度和轨道倾角对卫星可见性的影响，提出了配置惯性导航系统和载波相位时间差分的方案分别解决可见星缺失和几何精度因子过大的问题。

现有的相关研究工作分别从不同方面分析了高轨GNSS信号可用性。但是，由于高轨卫星处在一个综合了弱信号、强干扰、高动态的复杂环境中，因此，需要综合考虑各种因素的影响从而对高轨GNSS信号可用性进行全面评估。基于此，本文从GNSS卫星可见性、多普勒频移及其变化率和几何精度因子等方面对高轨GNSS信号可用性进行系统的分析。

1 高轨卫星与GNSS星座空间分布

探究GNSS信号的可用性，首先须明确高轨卫星与GNSS卫星的空间分布，如图1所示。

图1 高轨卫星与GNSS卫星空间位置示意图Fig.1 Schematic diagram of high orbit and GNSS satellites

本文分别以中国发射的GEO高分辨率光学遥感卫星高分4号(GF-4)和型号为AMSAT-OSCAR 40(AO-40)的 HEO卫星为对象，模拟高轨卫星的运行轨道。仿真周期设置为1 s，仿真时长设置为卫星的运行周期，利用MATLAB模拟得到其位置和速度信息。表1所示为GF-4/AO-40卫星的轨道参数。其中GF-4卫星的轨道平面与赤道平面重合，AO-40卫星的轨道平面与赤道平面夹角为6.04°。

表1 GF-4/AO-40卫星轨道参数Table 1 Orbital parameters of GF- 4/AO- 40 satellite

通过设计GNSS全系统导航星座模拟器可得GNSS星座的空间位置。以J2000.0地心惯性坐标系(Earth Centered Inertial,ECI)为空间基准，以协调世界时(UTC)为时间基准，仿真时间间隔设置为1 s，根据卫星星历提供的轨道参数及修正量，解算任意时刻GNSS卫星的位置和速度，利用MATLAB搭建星座模拟器，其轨道参数和星历可通过查询相关资料获得，如表2所示。

表2 GNSS星座的轨道参数Table 2 Orbital parameters of the GNSS constellation

GPS的空间部分由24颗MEO卫星组成，均匀分布在6条升交点赤经相差60°的轨道上，运行周期均为11小时58分。GLONASS星座包括24颗卫星，均匀分布在3条轨道倾角均为64.8°的近圆轨道，轨道的升交点赤经两两相差120°，运行周期均为11小时15分44秒。BDS星座由5颗GEO卫星、27颗MEO卫星、3颗IGSO卫星组成。GEO卫星的轨道高度为36 000 km，在赤道上空分别定点于东经58.75°、80.3°、110.5°、139.9°和160°；IGSO卫星的轨道高度为36 000 km，轨道倾角为55°；MEO卫星的轨道高度为24 500 km，分布在轨道倾角均为55°的3条轨道。Galileo系统空间部分由30颗导航卫星组成，均匀分布在3条轨道倾角为56°的轨道上，每条轨道上有9颗工作卫星和1颗备用卫星。

2 GNSS卫星可见性分析

当GNSS信号传输到高轨卫星并被捕获利用时，则称GNSS卫星可见。由此可知，GNSS卫星可见需满足两个条件：GNSS信号可传输到高轨卫星和GNSS信号强度高于接收机灵敏度。GNSS卫星可见是GNSS信号可用的前提。GNSS卫星可见性分析即以GNSS卫星可见的条件为基础，通过对GNSS信号的空间覆盖特性和强度分布特性的分析，探究GNSS卫星的可见性。

2.1 GNSS信号的空间覆盖特性

根据导航卫星天线的设计要求，GNSS卫星主天线下行频率波束呈圆锥形。由于地球的遮挡，高轨卫星只有位于主波束边缘构成的环形锥内才能接收到GNSS信号[15]，如图2所示。信号传播方向与导航卫星-地心连线方向所成夹角记为发射角β。发射信号的主瓣波束宽度为42.6°，其中有27.7°宽的信号被地球遮挡，无法传输到高轨卫星[14]。由于大部分主瓣信号被遮挡，必须充分利用旁瓣信号进行导航。

图2 GNSS信号空间构型Fig.2 Spatial configuration of GNSS signals

通过建立GNSS传播链路模型分析旁瓣信号的可用范围。接收机的信号接收功率是由GNSS卫星信号发射功率、发射天线增益、自由空间传播损耗以及接收天线增益直接决定的[16]，接收功率Pr为

(1)

由式(1)可以看出，GNSS信号传播链路可分为信号发射端、空间传输过程、信号接收端三个阶段。链路示意图如图3所示。

图3 GNSS信号传播链路示意图Fig.3 Diagram of GNSS signal propagation link

GNSS信号发射天线作为信号传播链路的起点，其Pt和Gt对信号接收功率的影响较大。由于各GNSS信号发射天线的性能类似且GPS的数据文件最为齐全，因此以GPS信号为例进行说明。根据GPS 系统接口数据文件[7,17]可得GPS天线Pt=26.8 W，Gt大小如图4所示。

由图4可知，发射天线增益与发射角有关。当发射角约为10°时，主瓣信号峰值增益为15 dB。第一旁瓣信号峰值出现在发射角约为32°处，信号强度约为3 dB。第二旁瓣信号较弱，其信号强度始终低于0 dB。

图4 GPS卫星发射天线增益曲线Fig.4 Gain curve of GPS satellite transmitting antenna

GNSS信号在空间传输过程中，主要受到自由空间传播损耗的影响。自由空间传播损耗与发射信号波长λ和传输距离d有关。此外，当GNSS信号传播链路接近地球表面时，信号会受到大气损耗的影响。由于高轨环境中这部分信号占总信号的比例较小，因此可忽略不计。根据GPS星座模拟结果和GF-4的轨道数据可得GF-4运行周期内信号的自由空间传播损耗，如图5所示。

图5 GF-4运行周期内信号的自由空间传播损耗Fig.5 Free space propagation loss of signals in GF- 4 period

信号接收天线是GNSS信号传播链路的终点，其Gr会对信号接收功率产生影响。实际工程中，针对不同的任务需求可采用不同类型的接收天线。为了简化分析，本文假定高轨卫星上的信号接收天线采用0 dB全向增益天线。根据GPS发射信号功率、发射天线增益、自由空间传播损耗和接收天线增益，可得GPS信号接收功率方向图，如图6所示。

由图6可知，当发射角绝对值为0°～21.3°时，信号接收功率较高，接收功率范围为-173～-164 dBW，接收到的信号为主瓣信号；当发射角绝对值为30°～40°时，信号接收功率出现第二峰值，接收功率范围为-185～-174 dBW，接收到的信号为第一旁瓣信号。因此，可用GNSS信号空间覆盖区域如图7所示。图中，GF-4卫星质心记为G，GNSS卫星质心记为S，地球地心记为O。ROG为GF-4卫星到地球的距离；ROS为GNSS卫星到地球的距离；RSG为GF-4卫星到GNSS卫星的距离；r为GF-4卫星与GNSS卫星连线到地心的距离。OG与SG的夹角记为α；OS与SG的夹角记为β。

图6 GF-4运行周期内GPS信号接收功率方向图Fig.6 Direction diagram of GPS signal’s receiving power in GF- 4 period

图7 可用GNSS信号空间覆盖区域Fig.7 Spatial distribution of available GNSS signals

图7中，主瓣信号的发射角绝对值范围为13.8°～21.3°，第一旁瓣信号(下文所述旁瓣信号均指第一旁瓣信号)的发射角绝对值范围为30°～40°。

根据可用GNSS信号的范围可计算GNSS信号能传输到GF-4卫星的条件。

首先，GNSS信号能传输到GF-4卫星的前提是不受地球的遮挡。根据空间分布关系，可表示为

r>Re

(2)

式中：r=ROG·sinβ；Re为地球半径。

其次，只有当GF-4卫星位于导航卫星的天线波束范围内时，GNSS信号方可传输到GF-4卫星。根据空间分布关系，在△SOG中，由余弦定理可得

(3)

根据β的定义，β即为导航卫星的信号发射角。由前文分析可知，可用GNSS信号的β范围为13.8°<|β|<21.3°或30°<|β|<40°。

将β的范围代入到式(3)中可得

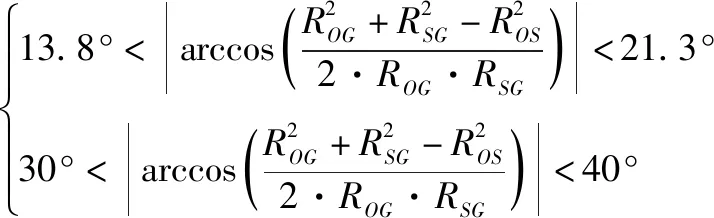
(4)

综上所述，式(2)和式(4)即为GNSS信号可传输到GF-4卫星的条件。

2.2 GNSS信号的强度分布特性

信号接收功率的强弱不能完整地描述信号的清晰程度或质量好坏，通常用载噪比C/N0衡量信号相对于噪声的强弱：

(5)

式中：N0与等效温度有关，对于一般的接收机来说，其典型值为-205 dBW/Hz[16]。

将所有可传输到GF-4/AO-40卫星所在位置的GNSS信号均视为可接收的信号。根据可用GNSS信号的发射角范围，结合GNSS星座模拟结果和GF-4/AO-40轨道数据，可得GF-4/AO-40运行周期内接收到的信号数，如图8所示。同时，基于所得的信号发射天线不同方向上增益数据以及信号自由空间传播损耗的计算公式，根据式(1)可得GF-4/AO-40卫星接收GNSS卫星信号的载噪比，如图9所示。

图8 卫星运行周期内接收到的信号数量Fig.8 The number of signals received in operational period of satellites

图9 运行卫星接收GNSS信号的载噪比Fig.9 The carrier-to-noise ratio of GNSS signals received by operational satellites

由图8(a)可知，可接收信号多数来源于旁瓣信号，这是因为主瓣信号大部分受到地球的遮挡，因此GF-4卫星须充分利用旁瓣信号进行导航。由图9(a)可知，主瓣信号的C/N0较高，主要分布在34～36 dB·Hz，旁瓣信号C/N0较低，主要分布在20～22 dB·Hz。需要注意的是，由于旁瓣信号较弱，接收旁瓣信号除了对接收机灵敏度有较高要求外，接收机还需同时采用互相关抑制技术去消除接收强弱信号产生的“互相关”干扰。

由图8(b)可知，AO-40卫星在近地点附近时，接收的信号多数为主瓣信号，随着AO-40卫星接近远地点，主瓣信号数迅速下降，接收的信号多数为旁瓣信号。由图9(b)可知，AO-40卫星接收的主瓣、旁瓣信号C/N0在整个轨道周期内均随轨道高度的增加而减小。主瓣信号C/N0分布在33～53 dB·Hz，旁瓣信号C/N0较低，主要分布在19～28 dB·Hz。

分析可知，无论是GF-4卫星还是AO-40卫星，必须充分利用数量较多的旁瓣信号进行导航，而旁瓣信号C/N0比主瓣信号C/N0低约14 dB·Hz，必须选择灵敏度数值较低的星载接收机，方可满足GNSS信号强度高于接收机灵敏度的条件。当同时满足GNSS信号可传输到高轨卫星和GNSS信号强度高于接收机灵敏度的条件时，GNSS卫星可见。

2.3 GNSS卫星可见性分析

利用GNSS星座的模拟结果和GF-4卫星的轨道数据，将满足GNSS卫星可见条件的卫星视为可见星，可得GF-4运行周期内四大导航系统的可见星数，如图10所示。接收机灵敏度分别设置为35 dB·Hz和20 dB·Hz，设置为35 dB·Hz时仅能接收主瓣信号，设置为20 dB·Hz时可同时接收主瓣信号和旁瓣信号。利用单个系统导航时至少需要4颗可见星才可解算出导航信息，即可见星数的阈值为4颗。表3为各导航系统可定位弧段占全程的百分比。

表3 可定位弧段占全程的百分比Table 3 The percentage of navigable arcs in the whole process

由图10、表3可知，当只接收主瓣信号时，各导航系统的可见星数较少，可定位弧段占全程百分比均低于5%，其中利用GLONASS系统全程均不可定位。当同时接收主瓣、旁瓣信号时，各系统的可见星数显著提高，可定位弧段占全程百分比较大，均高于74%。其中，BDS系统可实现全程定位，可定位弧段占比最低的GLONASS系统也达到74.59%。

利用四星座组合导航时，可得GF-4运行周期内GNSS全系统的可见星数如图11所示，对可见星数统计并绘制可见星数饼状图，如图12所示。需要说明的是，由于各导航系统的钟差不同，四星座组合导航时可见星数的阈值增加到7颗。

图11 GF-4运行周期内GNSS全系统可见星数Fig.11 The number of visible satellites in the whole GNSS system during the GF- 4 period

图12 GF-4运行周期内GNSS全系统可见星数饼状图Fig.12 The pie chart of the number of visible satellites in the whole GNSS system during the GF- 4 period

由图11可知，四星座组合导航时，GF-4运行周期内可见星数显著提高。由图12可知，四星座组合导航时，仅接收主瓣信号即可使可见星数达到阈值的弧段占总弧段的比例达到35%；若同时接收旁瓣信号，整个周期内可见星数均高于阈值，可见星数激增到17颗以上，GNSS卫星的可见性较强。

3 多普勒频移及其变化率的影响分析

GNSS信号的多普勒频移及其变化率与高轨卫星相对于GNSS卫星的运动特性有关。相较于地面用户，高轨卫星的动态性更强，特别是在机动变轨阶段。由此造成GNSS信号的多普勒频移及其变化率更大，对信号的捕获、跟踪性能产生不良影响，进而影响GNSS信号的可用性。

3.1 对信号捕获的影响

考虑对单个卫星信号处理的情况，以GPS信号为例进行分析。接收机接收到GPS信号后，经射频前端下变频和采样处理后得到数字中频信号，其模型为

r(n)=Ac(n-τ)d(n-τ)cos[2π(fIF+fd)n+φ0]+w(n)

(6)

式中：A为信号幅值；c(·)为伪随机码；d(·)为导航数据；fIF为中频信号频率；fd为多普勒频移；φ0为初始载波相位；w(·)为高斯白噪声；τ为码相位延迟。

本地产生复信号并与GPS信号进行相关运算，将相关运算的结果进行相干累积，相干累积的时间记为Tcoh。相干累积的采样点数记为N，则有N=Tcoh/Ts，Ts为中频信号采样周期，则相干累积的结果为

(7)

由于接收机捕获信号时间的实测数据无法获得，可用捕获算法执行时间和捕获算法重复运算次数去近似代表实际捕获时间。其中，接收机的启动方式为冷启动，捕获算法采用并行码相位搜索。以对GPS信号的捕获为例进行说明，对其他GNSS信号的捕获情况类似。图13为多普勒频移不同时的捕获情况。

图13 多普勒频移不同时的捕获情况Fig.13 The acquisition case of different Doppler frequency shift

根据GNSS星座模拟结果和AO-40轨道数据，可得AO-40运行周期内各导航系统导航信号的多普勒频移，如表4所示。接收机的灵敏度设置为20 dB·Hz。

表4 各导航系统导航信号的多普勒频移Table 4 Doppler frequency shift of each navigation system’s navigation signals

AO-40卫星在近地点附近运行速度较大，信号的多普勒频移较大。由表4可知，各导航系统信号多普勒频移的最大值均在40 kHz以上，BDS系统导航信号的多普勒频移负向最大值最高可达-63.35 kHz。随着轨道高度增加，AO-40卫星运行速度减小，远地点附近接收的信号多普勒频移较小，整个周期内各导航系统信号多普勒频移的平均值均在±2 kHz内。已知地面用户接收的GNSS信号多普勒频移一般为±5 kHz，结合图13可知，与地面用户相比，AO-40近地点附近较大的多普勒频移会使捕获时间增加40～70 s，捕获算法重复运算次数增加140～220次。相对于数量级为104的AO-40轨道周期来说，增加的捕获时间可忽略不计。远地点多普勒频移的影响则更小。因此GNSS信号的多普勒频移对信号的捕获时间虽有影响，但影响较小。

(8)

图14 衰减因子的变化曲线Fig.14 Change curve of attenuation factor

根据GNSS星座模拟结果和AO-40轨道数据，可得AO-40运行周期内各导航系统导航信号多普勒频移变化率，如表5所示。接收机的灵敏度为20 dB·Hz。

表5 各导航系统导航信号的多普勒频移变化率Table 5 Doppler frequency shift rate of each navigation system’s navigation signals

近地段AO-40卫星的动态性较强，GNSS信号的多普勒频移变化率较大。由表5可知，GLONASS系统导航信号多普勒频移变化率正向最大值最大，为14.94 Hz/s，BDS系统导航信号多普勒频移变化率负向最大值最大，为-51.41 Hz/s。随着轨道高度的增加，动态性减弱，整个周期内各导航系统信号多普勒频移变化率平均值均小于1 Hz/s。结合图14可知，虽然高轨GNSS信号的多普勒频移变化率高于地面用户，但带来的衰减依旧较小，对捕获性能影响较弱。

3.2 对信号跟踪的影响

GNSS信号跟踪环路由载波跟踪环路和码跟踪环路组成，分别跟踪接收信号中的载波与伪码。不管是载波跟踪环还是码跟踪环，都可用一个解析的相位锁定环路模型衡量其性能[19]。相位锁定环路简称锁相环，通过调整输出信号的相位，使输出信号与输入信号的相位保持一致，从而实现对载波与伪码的跟踪。以常见的二阶锁相环为例进行分析，其基本构成如图15所示。

图15 锁相环的基本构成Fig.15 The basic structure of PLL

二阶锁相环路由鉴相器、环路滤波器和压控振荡器组成。根据各环节的传递函数可得系统函数H(s)为[19]

(9)

式中：τ1，τ2为环路滤波器的参数；Ko为压控振荡器增益；ωn为特征频率；ξ为阻尼系数。

环路带宽又称噪声带宽，是影响跟踪环路性能的重要指标，控制着进入环路的噪声量多少，定义为

(10)

式中：H(jω)为跟踪环路频域特性函数。

根据式(9)～(10)可求得二阶锁相环的环路带宽为

(11)

环路带宽BL分别为10 Hz、30 Hz和60 Hz情况下，锁相环的相位阶跃响应曲线如图16所示。

图16 不同环路带宽情况下阶跃响应曲线Fig.16 Step response curves for different loop bandwidths

由图16可知，环路带宽较大时，锁相环可快速锁定信号进入稳定状态。但较大的环路带宽会使输出信号中噪声较多，严重时导致暂态过程不收敛，即环路失锁。环路带宽较窄时，环路的滤波效果较好，环路跟踪误差较小，但环路收敛较慢且GNSS信号高动态所致的载波频率和相位变化中有用高频信号成分会同噪声一起被滤除，破坏了接收信号的真实性，也容易使跟踪环路失锁，导致接收机无法输出导航参数。

由于高轨GNSS信号的载噪比较低，跟踪环路需要较窄的环路带宽以获得更多的有用信息。而较窄的环路带宽在多普勒频移及其变化率较大时容易导致跟踪环路失锁，因此多普勒频移及其变化率会影响跟踪性能。通过卡尔曼滤波等方法可实现对环路带宽的动态调节[20]，以降低多普勒频移及其变化率对跟踪性能的影响。

4 GNSS不同组合星座几何精度因子分析

定位精度是评估GNSS系统性能最重要的指标。影响定位精度的因素有测量误差和精度因子。精度因子描述的是从测量误差到定位误差的放大量。测量误差在实际工程中无法避免。在测量误差存在的情况下，应尽可能减小精度因子，从而提高系统的定位精度。精度因子中的几何精度因子(GDOP)包含了其他所有精度因子的参数，反映了GNSS卫星相对于接收机的空间几何分布对导航定位精度的影响。

4.1 几何精度因子模型

设接收机的空间位置坐标为[xr,yr,zr]T，第i颗卫星的空间位置坐标为[xi,yi,zi]T，则伪距观测方程为

(12)

联立四个或四个以上不同卫星的伪距观测方程，并保留测量误差项，伪距定位方程为

(13)

式中：εxr,εyr,εzr和εδtr为测量误差引起的定位、定时误差；ln(xr,k-1)为接收机与GNSS卫星间的单位方向矢量，若将方向矢量组成的矩阵记为G，即

(14)

利用最小二乘法求解方程组(13)，求解出定位、定时误差为

(15)

(16)

H=(GTG)-1

(17)

H矩阵通常称为权系数阵，则几何精度因子为

(18)

式中：hii为权系数阵的对角元素，i=1,2,3,4。

因此，导航系统的定位误差可表示为

(19)

展开为

(20)

式中：σp为定位误差的方差向量。

通过GDOP的推导可以看出，GDOP的大小与G有关。而G是由接收机与GNSS卫星方向单位矢量组成的矩阵，这表明GDOP的大小取决于GNSS卫星相对于接收机的空间几何分布。在高轨环境下，由于GNSS卫星可见性降低且可见星的几何构型较差，导致GDOP激增，定位误差较大，进而对GNSS信号可用性产生影响。

4.2 几何精度因子分析

根据GNSS星座模拟结果和AO-40卫星轨道数据可得AO-40运行周期内GDOP值低于阈值的弧段占全程的百分比，如图17所示。其中，GDOP的阈值为10，接收机灵敏度分别设置为35 dB·Hz和20 dB·Hz。

图17 GDOP值低于阈值的弧段占全程的百分比Fig.17 The percentage of arcs below the GDOP threshold in the whole process

由图17可知，同时接收主、旁瓣信号使GDOP值低于阈值的弧段占全程的百分比显著提高，表明定位精度较高的弧段占比增加。其次，多系统组合相对于单系统而言，具有更好的星座构型，可见星数更多，GDOP值低于阈值的弧段占比更大。

改变接收机灵敏度，统计不同接收机灵敏度时GDOP不同的弧段占全程的百分比，如表6所示。

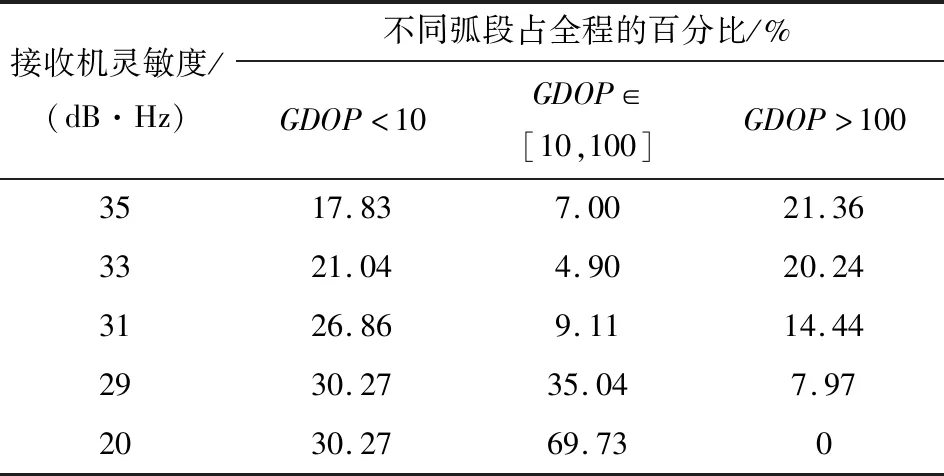
表6 不同接收机灵敏度时各弧段占全程的百分比Table 6 The percentage of each arc in the whole process with different receiver sensitivity

表6中，随着接收机灵敏度的提高，可定位弧段占全程的百分比逐渐增加。当接收机灵敏度为20 dB·Hz时，可实现全程定位且定位误差较大的弧段(GDOP>100)占全程的百分比为0。接收机灵敏度的提高会使定位精度高的弧段(GDOP<10和GDOP∈ [10,100])占全程百分比增加，定位误差较大的弧段(GDOP>100)占全程百分比减小。当接收机灵敏度为20 dB·Hz时，定位精度最高的弧段(GDOP<10)占全程百分比高达30.27%。

5 结 论

本文从GNSS信号的空间覆盖特性、强度分布特性、多普勒频移及其变化率以及几何精度因子等方面对高轨GNSS信号可用性进行了全面系统的分析，通过分析可得到以下结论：

(1) 高轨环境中，受地球遮挡的影响，大量的主瓣信号无法传输到高轨卫星，GNSS卫星的可见性较差，不能满足最低4颗导航卫星的要求。而旁瓣信号不受地球遮挡且第一旁瓣信号强度满足GNSS卫星可见的条件，因此利用旁瓣信号进行导航可改善高轨GNSS卫星的可见性。

(2) 与地面及中、低轨环境相比，高轨环境中GNSS信号的传输距离较远，因此到达高轨卫星所在位置的GNSS信号自由空间传播损耗较大。到达GF-4卫星所在位置的GPS信号自由空间传播损耗范围为-192.49～-187.25 dBW。此外，在同一轨道高度处，信号的传输距离和自由空间传播损耗均随信号发射角的增加而减小。由于旁瓣信号的信号发射角大于主瓣信号，因此旁瓣信号的自由空间传播损耗小于主瓣信号。对于GF-4卫星来说，GPS的主瓣信号自由空间传播损耗范围为-192.49～-191.18 dBW，旁瓣信号的自由空间传播损耗范围为-191.18～-187.25 dBW。

(3) 高轨环境中，GNSS信号接收功率的空间分布与信号发射角和轨道高度有关。在同一轨道高度处，由于主瓣信号和旁瓣信号的发射角不同，因此接收功率存在显著差异，旁瓣信号接收功率的峰值比主瓣信号低10 dBW以上。GF-4卫星所接收GPS主瓣信号的接收功率范围为-192.35～-165.42 dBW ，旁瓣信号接收功率范围为-180.77～-175.51 dBW。

(4) 高轨环境中，采用单星座导航时GNSS可见星数较少，GNSS卫星可见性较差，且可见星的几何构型较差，GDOP较大，进而导致定位误差较大。而多星座共用不仅可以大幅提高GNSS可见星数，改善GNSS卫星可见性，还可以优化导航可见星的几何构型，显著降低GDOP，提高导航精度。GF-4卫星利用全系统导航且同时接收主、旁瓣信号时，整个周期内可见星数均在17颗以上，同时GDOP大幅减少，可见性显著增强。

(5) 与地面用户相比，高轨卫星动态性较强，因此高轨卫星所接收GNSS信号的多普勒频移及其变化率较大，AO-40卫星运行周期内多普勒频移最高为-63.35 kHz，多普勒频移变化率最高为-51.41 Hz/s。高轨环境中GNSS信号较大的多普勒频移会延长捕获时间，较大的多普勒频移变化率会造成捕获相干峰的衰减，但增加的捕获时间较短，造成的衰减较弱。AO-40卫星近地点附近较大的多普勒频移仅使捕获时间增加40～70 s，因此多普勒频移及其变化率对信号捕获的影响较小。同时，通过采用动态调节环路带宽的方法可降低多普勒频移及其变化率对跟踪性能的影响。

综合来看，由于地球的遮挡以及信号传输距离的增加，高轨环境中，GNSS卫星可见性较差，GDOP较大，进而导致GNSS信号可用性较差。通过提高接收机的灵敏度，可增加GNSS可见星数并改善可见星的几何构性，提升高轨GNSS信号的可用性。后续工作将围绕对弱GNSS信号的捕获、跟踪算法展开。