基于集群智能优化的模糊神经网络设计与应用

王永海，郭 珂*，方 岳，叶玉玲

(1.北京航天长征飞行器研究所，北京 100076；2.中船重工集团第七一○研究所，湖北 宜昌 443003)

0 引 言

模糊神经网络(FNN)是一种将模糊推理系统和神经网络有机结合，功能上与模糊推理系统完全等价的自适应网络，具有强大的学习和推理能力。它已经在非线性系统辨识、控制、故障诊断等领域得到了广泛应用[1-4]。

王立新[1]将模糊系统作为万能逼近器，构造了一个前馈三层FNN，用于逼近非线性函数。韩红桂等人[4]提出了一种基于混合梯度下降算法的模糊神经网络，应用于非线性系统建模与污水处理过程关键水质参数预测时，表现出了较好的收敛速度和泛化能力。Wang[5]提出了一种具有新型模糊隶属度函数的模糊神经网络，并在非线性时变系统的辨识[6-7]中取得了较好的结果。叶玉玲[8]基于模糊粗糙隶属函数，建立了一种五层结构的模糊粗糙神经网络，并通过一种混合智能优化算法优化了网络结构和参数，取得了较好的精度和泛化能力。刘俊强[9]对FNN的结构和学习算法进行了深入的研究，给出了四种FNN结构，其中典型的基于零阶TS模糊逻辑系统的多输入单输出FNN结构分为五层：输入层、模糊化层、模糊推理层、归一化层和输出层。这种FNN具有设计方法简单，物理意义明确，可逼近任意非线性函数的特点。在其结构设计过程中，输入层和输出层根据实际系统确定，只需要给出每个输入空间划分的子空间数目，就确定了模糊化层、规则层和归一化层神经元的个数及连接。FNN的参数设计，即FNN的学习，是一种多变量寻优技术，一般把参数分为前件参数和结论参数，分别学习。先确定前件参数，然后用最小二乘法得到结论参数。前件参数的学习一般采用BP算法[10]、单纯形算法、遗传算法[11]、粒子群优化算法[12-13]等。但是，这样设计出来的FNN结构一般比较庞大，如果有4个输入，每个输入空间被划分为3个子空间，那么模糊化层有12个神经元，规则层和归一化层有81个神经元，模糊化层与规则层之间共有324个连接。复杂的FNN结构一方面增加了计算量，另一方面也降低了系统的泛化能力。

智能优化技术如遗传算法和粒子群算法等在神经网络结构及参数辨识中得到了广泛的应用，并取得了很好的结果。Leung[11]和Tsai[14]分别用改进的实数编码的遗传算法和HTGA算法，同时对给定隐层节点数的情况下前馈神经网络的连接权和参数进行进化设计，在保证精度的情况下，有效简化了神经网络的结构。文献[15]用递阶结构的蚁群-粒子群算法来优化FNN网络参数，从而实现神经网络的非线性建模与控制。还有采用多种群协同进化来优化RBF网络结构和参数[16]，利用删除法确定RBF网络隐层节点数，用细菌群体趋药性算法来确定参数的方法[17]等。

本文提出了一种混合集群智能优化算法，给出了其对应的实数编码形式(RIOA)和二进制编码形式(BIOA)。把FNN的结构用一个布尔变量来表示，然后利用协同进化的思想，分别用BIOA和RIOA对FNN的结构参数和前件参数同时进行优化设计，结论参数采用最小二乘法[18]计算得到。用此方法进行FNN设计，对太阳黑子数目进行建模，实验验证了方法的有效性。

1 模糊神经网络结构和参数分析

在图1所示的基于零阶TS模糊逻辑系统的多输入单输出FNN结构设计中，设FNN的输入为x=(x1,x2,…,xm)，其中xi的输入空间被划分为ni个子空间，i=1,2,…,m，对应的模糊集合记为Ai={Aij,j=1,2,…，ni}。将模糊量Aij的隶属函数记为μij(xi)=μAij(xi)，则

(1)

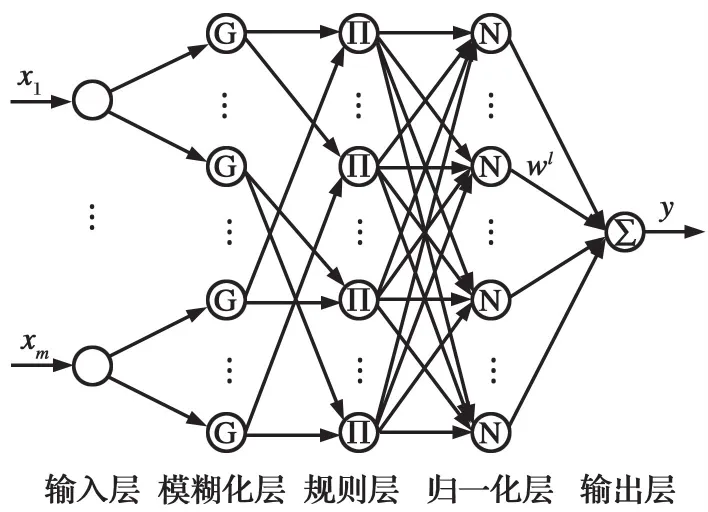
图1 模糊神经网络结构Fig.1 Structure of fuzzy neural network

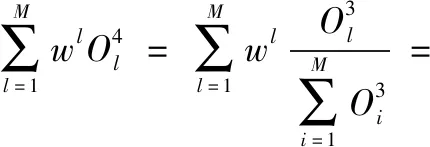
(2)

FNN的设计可以表示为:对于训练样本Dq={u1q,u2q,…，unq,fq}，q=1,2,…，Q，寻找参数集S=S1+S2={ast,bst,L}+{wl}，其中，s=1,2,…,N；t=1，2，…，n，使如下参数最小化：

(3)

FNN的输出是结论参数集的线性函数，因此，在固定前件参数和网络结构的条件下，采用最小二乘辨识得到的结论参数是最优的。故而在FNN参数辨识中，主要任务即是寻找合适的参数集{ast,bst,L}。

2 混合集群智能优化算法BIOA和RIOA

考虑如式(4)所示的全局数值优化问题:

minf(x)=f(x1，x2，…，xn)

(4)

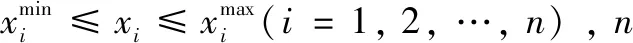
混合集群智能优化算法BIOA和RIOA是一种算法的两种不同编码形式：二进制编码和实数编码。其基本思想借鉴了遗传算法的交叉和变异操作、粒子群优化算法的相关操作[19]，并对其进行了改进。其基本过程如图2所示。

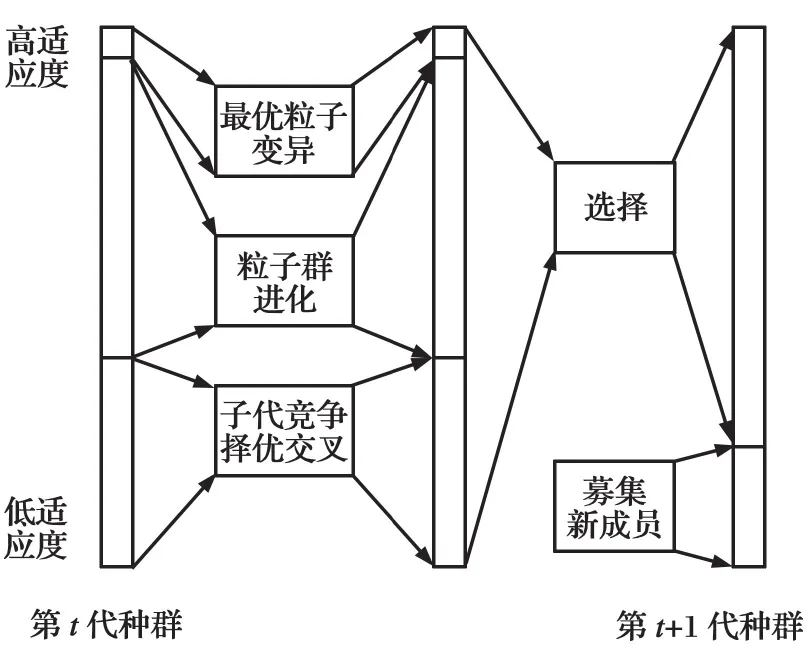
图2 混合集群智能优化算法BIOA和RIOA进化示意图Fig.2 Evolution figure of hybrid swarm intelligent optimization algorithm BIOA and BIOA

算法可以简单地描述为：

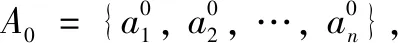
Step 2：计算各个体的目标函数值，并从小到大排序；令目标函数值最小的个体为a0，对应的目标函数值设为f0。如果满足结束条件|f0-fmin|≤es或者ns≥Ns，其中，fmin为目标函数全局最小值，则算法结束，返回a0。否则，转Step 3。

Step 3：对a0进行变异，如果变异后的个体目标函数值减小，则用变异后的个体更新。

Step 4：对目标函数值较大的(round(n·α))个个体进行PSO操作，并计算得到个体的目标函数值，如果有小于f0的个体，则用该个体更新a0。

Step 5：对剩余的个体按交叉概率β进行交叉操作，并计算得到个体的目标函数值，如果有小于f0的个体，则用该个体更新a0。

Step 6：对所有新个体按目标函数值从小到大进行排序，选择目标函数值较大的(round(n·γ))个个体进入下一代。

Step 7：随机生成(round(n·(1-γ)))个新的个体，加入到下一代中。计算这些个体的目标函数值，ns=ns+1，转Step 2。

2.1 二进制编码的混合集群智能优化算法BIOA

(5)

其中，rand(1)表示[0，1]之间的随机数，round(·)为取整操作。

第4步的PSO操作为

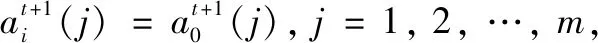
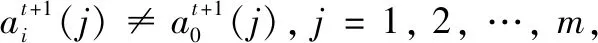
其中,δ为阈值，0<δ<0.5。

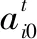
j=round(rand(1)·m)

2.2 混合集群智能优化算法RIOA

(6)

其中,λ∈[-0.5 0.5]，j=round(rand(1)·m)。

PSO操作为

(7)

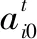
(8)

(9)

(10)

(11)

2.3 算法特点

混合集群智能优化算法BIOA和RIOA综合了遗传算法、粒子群优化算法和免疫算法的优点，改进了其算子，不仅大大提高了搜索的速度，同时也保证了种群的多样性，从而有效避免了早熟和局部收敛。本文所提混合集群智能优化算法为全局搜索算法，由于搜索范围覆盖了整个搜索域，因而总是可以找到全局最优解的，从理论上可以证明算法可按期望收敛到全局最优解，且算法是渐近稳定的。归纳起来，有如下特点：

(1)每一种单一的搜索算法，都因其自身固有模式而存在自身缺陷。由遗传算法、粒子群优化算法和免疫算法结合而成的混合集群智能优化算法BIOA和RIOA，其优化性能通常优于单一的任一种优化方法的优化性能。

(2)根据个体的目标函数值不同，采用不同的操作，大大降低了计算量，提高了搜索的效率。

(3)由于PSO算法可以灵活调节算法全局搜索和局部开发的平衡，这在一定程度上较有效地克服了算法早熟、局部收敛的缺陷，提高整体算法的搜索能力[20]。

(4)采用竞争择优的交叉算子代替常规的交叉算子，大大提高了搜索的速度，同时，由于搜索范围覆盖了整个搜索域，有利于避免局部收敛和保持种群的多样性。

(5)直接对最优个体进行变异操作，在RIOA中变异的幅度随进化代数自适应变化，增强了算法的局部搜索能力。

(6)募集新成员操作进一步保证了抗体群的多样性。

3 基于BIOA和RIOA协同进化的模糊神经网络设计

基于BIOA和RIOA的模糊神经网络设计是在给定ni的情况下，利用BIOA和RIOA协同进化，寻找最优的参数集{ast,bst,L}。协同进化示意图如图3所示。

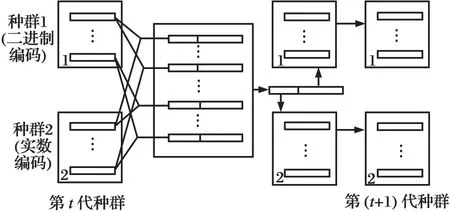
图3 BIOA和RIOA协同进化示意图Fig.3 Cooperative optimization figure of BIOA and RIOA

Step 1：随机生成NB个长度为L的二进制编码初始种群{a1,a2,…,aNB}和NR个长度为2m的实数编码种群{b1,b2,…,bNR}。给参数ec(或者Nc)和ξ赋值，nc=1。

Step 2：种群1和种群2的个体进行组合，得到NB·NR个完整的参数集个体{a1b1，…，a1bNR，a2b1，…，a2bNR，…，aNBbNR}。

Step 3：对每个个体aibj(1≤i≤NB，1≤j≤NR)，根据最小二乘法计算结论参数和目标函数值。令目标函数值最小的个体为最优个体a0b0。如果结束条件(最优个体对应的目标函数值|f0-fmin|≤ec或者nc≥Nc)满足，则结束，否则转到Step 4。

Step 4：用a0与种群2的个体进行组合，得到完整的参数集种群{a0b1,a0b2,…，a0bNR}。保持a0部分不变，利用优化算法RIOA对种群{b1,b2,…,bNR}进行进化，得到最优个体a0b′。

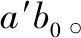
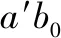
Step 7：nc=nc+1，转到Step 2。

其中，超级个体的变异操作包括：删除连接，增加连接(如果{a1，a2，…，aNB}中有为0的项)，对参数进行小的随机扰动，删除节点。其操作如下：

(1)删除连接

ifai=1 thenai=1-ai,

i=round(rand(1)·NB)

(2)增加连接

ifai=0 thenai=1-ai,

i=round(rand(1)·NB)

(3)对参数施加小的随机扰动

bi=bi+(rand(1)-0.5)ξ

(4)删除节点

aj=0，aj为所有与规则层中第i个神经元连接的连接值，i=round(rand(1)·M)。

ξ根据实际情况取较小的值。

4 实验及结果分析

太阳黑子的数目是年份的函数，这个函数是非线性、非稳态、非高斯的，很难对其进行预测。1700年至1980年的太阳黑子数如图4所示。文献[11]用改进的遗传算法进化神经网络的结构和参数，文献[14]用混合Taguchi遗传算法进化神经网络的结构和参数。和文献[11]相比，在相同的隐层节点下，文献[14]的方法不仅提高了精度，而且得到的神经网络结构也更加简化。本实验采用模糊神经网络来建立太阳黑子数目的模型，用混合集群智能优化算法BIOA和RIOA协同进化来优化FNN的结构和参数。

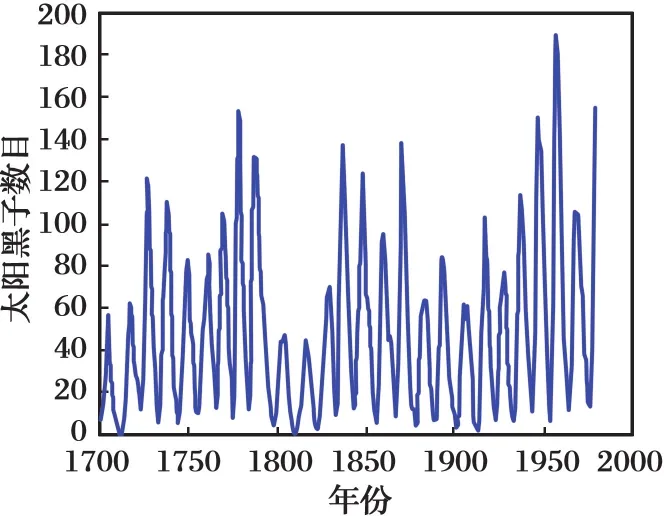
图4 1700年至1980年的太阳黑子数目Fig.4 Sunspot cycles from 1700 to 1980

作为比较，引入了用BP算法训练前件参数和最小二乘法得到结论参数的FNN设计方法(FNN-BP)。

(2)把数据集分为训练集和测试集，前180年(1705≤t≤1884)的数据作为训练集，被用来训练模糊神经网络，剩余数据作为测试集，用于测试训练好的神经网络。

(3)训练误差定义为

(12)

其中，y1(t)表示t年FNN输出的太阳黑子数目。

测试误差定义为

(13)

适应值定义为

(14)

(4) BIOA和RIOA中的参数取值为：种群规模NB=Ng=20，α=0.5，β=0.5，γ=0.8，停止条件为ns=1，nc=10。

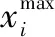
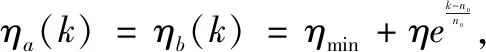
20次实验所得训练集上适应值结果如表1所示。

其网络类型中，FNN-BIOA/RIOA表示由BIOA和RIOA协同优化结构和参数得到的FNN；FNN-BP表示仅由BP算法和最小二乘法训练得到的FNN；NN-HTGA表示用HTGA优化结构和参数得到的三层前馈神经网络，其数据来源于文献[14]。由表1所列出的结果可以看出：(1)FNN-BIOA/RIOA得到的适应值(最优值和平均值)总是大于相同网络结构的FNN-BP，而且两者的适应值都随着网络规模的增大而增加。这也证明了网络结构越复杂，越能以更高的精度逼近非线性函数。(2) FNN-BIOA/RIOA得到的适应值平均值几乎都大于NN-HTGA，FNN-BP在网络结构大于[3 2 2]时也都优于NN-HTGA的最优值。随着隐层节点数的增加，NN-HTGA的适应值先增加后降低，当隐层节点数为6时，结构最优。这说明在对非线性系统进行建模时，FNN更容易得到更高的精度。(3) FNN-BIOA/RIOA和NN-HTGA得到的适应值的标准差几乎都在10-4这一数量级。对于平均值而言，标准差很小。由于FNN-BP的参数初值每次实验都相同，算法也相同，所以适应值标准差为0。这说明三种方法建立的网络模型精度都比较稳定。

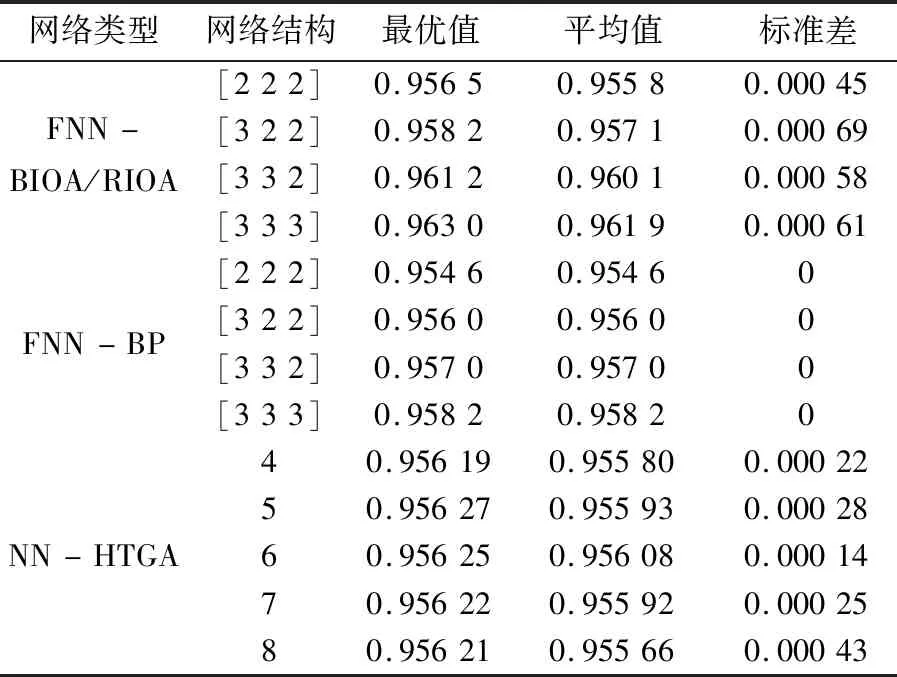
表1 训练集上适应值结果比较Table 1 Comparison of fitness values on train set

20次实验得到的适应值、训练集上的训练误差、预测集上的预测误差和连接数平均值如表2所示。图5给出了FNN-BIOA /RIOA方法的平均训练误差。

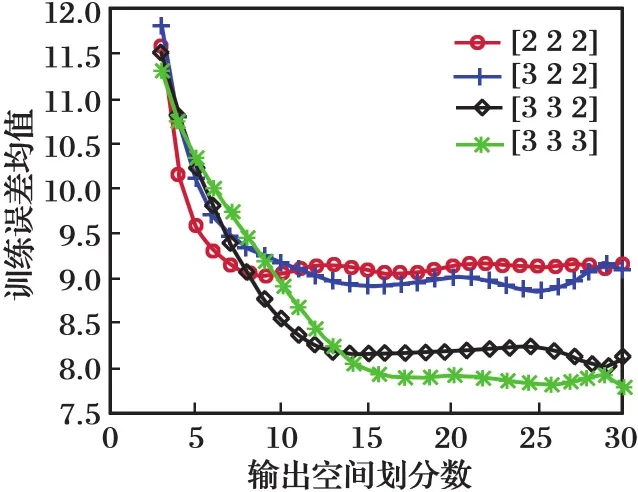
图5 FNN-BIOA /RIOA平均训练误差Fig.5 Average training error of FNN-BIOA /RIOA

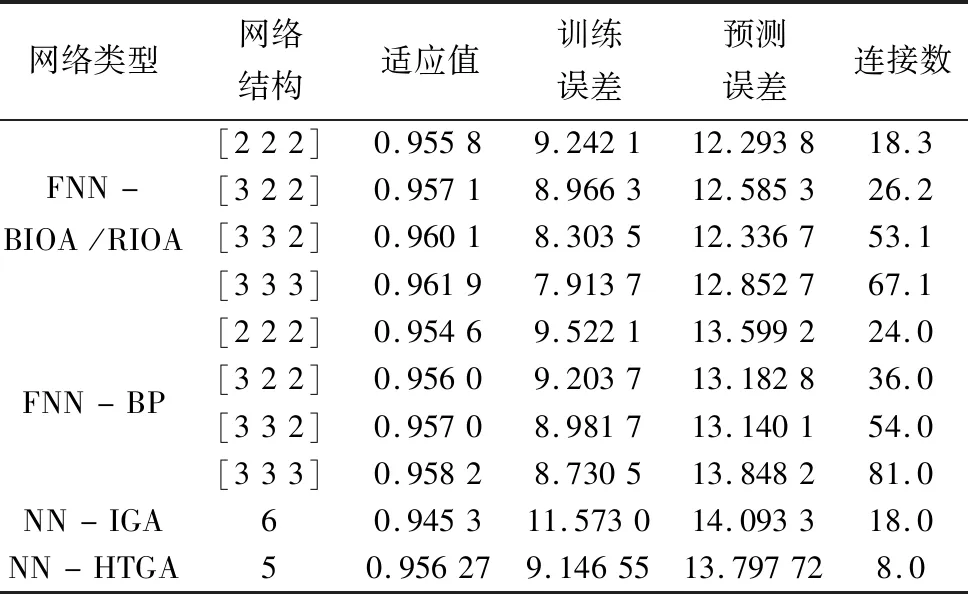
表2 网络性能和结构比较Table 2 Comparison of network performance and structure

其中，NN-IGA表示用IGA优化结构和参数得到的三层前馈神经网络，其数据来源于文献[11]。从表2的结果可以看出：(1)就训练误差而言，在相同的网络结构时，FNN-BIOA/RIOA比FNN-BP小，两者都低于NN-IGA的最优值。FNN-BIOA/RIOA在网络规模大于[2 2 2]时，FNN-BP在网络规模大于[3 2 2]时，两者的训练误差均低于NN-HTGA的最优值。(2)就预测误差而言，FNN-BIOA/RIOA得到的FNN预测误差最小，FNN-BP和NN-HTGA的预测误差大致相等，均低于NN-IGA。(3)就网络的复杂程度而言，FNN- BIOA/RIOA的连接数明显比FNN-BP少，这说明FNN-BP的结构中确实含有许多冗余的连接，而BIOA/RIOA可以有效地降低其冗余。

5 结 论

将典型的基于零阶TS模糊逻辑系统的模糊神经网络模糊化层和规则层之间的连接用一个布尔变量表示后，模糊神经网络的输入输出表达式中就包含了一个反映FNN结构的参数。把这个结构参数和模糊神经网络的前件参数分别放在两个种群中，用本文提出的混合集群智能优化算法BIOA和RIOA进行协同进化，得到最优的前件参数后用最小二乘法计算得到优化的结论参数。对太阳黑子数目的建模实验表明，本方法能得到比普通用BP算法和最小二乘算法得到的模糊神经网络和用三层前馈神经网络更高的精度和泛化能力，同时也能有效地简化模糊神经网络的结构。