考虑脱靶量和架构的导弹协同制导效能评估技术

郭正玉，李耀民，王超磊，史荣宗

(1.中国空空导弹研究院，河南 洛阳 471009；2.航空制导武器航空科技重点实验室，河南 洛阳 471009；3.95972部队，甘肃 酒泉 735000)

0 引 言

航空制导武器新技术、新概念和新方法的不断发展，使空空导弹的性能不断提升，但是制空作战环境的日益复杂，作战目标的不断增多，使传统的单枚导弹作战模式，在满足未来智能化空战场作战任务需求方面出现了不足。使用多枚空空导弹协同作战，通过导弹之间的信息共享实现配合协作，可以提高对目标的探测和毁伤，是提高作战效能的有效途径之一，能够大大丰富作战样式，满足智能化空战的作战需求[1]。

目前，关于导弹武器装备效能评估的研究不断深入，方法也很多，总体上分为专家评定法、试验统计法、作战模拟法、解析法和问卷调查法等。在导弹领域常用的效能评估方法包括：ADC效能分析法、层次分析法、系统效能分析法、信息熵效能分析法和区间数分析法等。ADC效能分析法由美国工业界系统效能咨询委员会提出，考虑武器系统工作的初始状态、工作中的可能状态和最后状态，其中A为系统的可用性(Availability)向量，表示任务开始执行瞬间，系统可能出现的工作状态的概率；D为可信性矩阵(Dependability)，表示系统从初始工作状态转移到其他工作状态的概率；C为能力矩阵(Capability)，表示在最后的可能状态中达到的效能指标值。ADC效能分析法能够根据作战系统的构成、初始使用状况以及作战中出现的作战状况动态评估作战中的效能。作战系统的作战能力是效能评估中的关键因素，能力的准确计算是合理效能值的基础[2]。层次分析法是多准则决策方法，它将复杂的综合问题分解为若干个组成要素，并将这些要素按支配关系分组形成递进层次结构，通过比较的方式确定层次中各因素的相对重要性，综合决策确定重要性排序[3]。系统效能分析法(SEA)强调在相同的环境下，系统的独立建模和分析，从匹配程度定量分析系统效能。其优点是贴近效能评估的基本含义，作为一个动态的客观分析系统效能的方法，它能充分体现出系统构件、 组织和战术的变化对系统效能的影响。信息熵效能分析法利用熵技术确定评估指标中各部分的权重。如果通过其他算法确定各部分的权重，也可以进一步运用熵技术来修正先前决定的优先权重，有助于形成更加准确的决策。区间数分析法(TOPSIS)的基本原理是逼近理想解，借助多属性决策问题，通过检测评价对象与最优解、最劣解的距离来进行排序，若评价对象最靠近最优解同时又最远离最劣解，则为最好；相反，若评价对象最靠近最劣解同时又离最优解最远，则为最差[4-7]。目前使用上述方法进行导弹效能评估的应用和分析有很多，但几乎都是针对单枚导弹的，针对空空导弹本身及多枚空空导弹协同制导攻击过程中，考虑导弹成员之间的架构和协同制导带来的综合作战效能的提升来评价多枚空空导弹综合效能的研究还不多见。

本文在现有导弹效能评估方法的基础上，建立了协同制导模型，分析了不同架构下导弹攻击构型的攻击效果，提出了一种以导弹性能参数为基础的，考虑多枚导弹协同制导脱靶量、制导时间和导弹编队架构的效能评估方法，并结合美国现有的具体导弹型号进行了仿真和评估分析。

1 协同制导效能评估模型

1.1 多弹协同制导模型

协同制导是多枚导弹通过弹道间的相互配合，共同攻击一个或者多个目标。本文以三枚导弹攻击一个机动目标为例，将导弹和目标视为质点，弹目几何关系如图1所示。

图1 多弹协同攻击示意图Fig.1 Multi-missile cooperative attack

图1中，Mi和T为第i枚导弹和目标，ri为Mi与T的相对距离，qi为Mi的视线角，vmi和vt为Mi和T的速度，θmi和θt为Mi和T的弹道倾角，ami和at为Mi和T的法向过载，其中i=1,2,…,n，i为导弹数量。协同制导方程如下[8-9]：

(1)

由于本文主要研究协同制导效能评估技术，因此这里只给出计算协同制导参数的多导弹协同制导模型，推导过程从略：

(2)

将多导弹协同制导模型带入动力学模型，计算得到攻击的脱靶量mi、攻击时间差Δsi作为效能评估的指标参数。

1.2 基于信息熵的效能评估法

一个系统的熵是该系统有序无序程度的度量，熵越大，系统越无序,反之则系统有序。利用熵算法可以确定评估指标中各属性的权重。假设评估中存在m枚导弹，每枚导弹又具有n个指标参数，对于这个多目标决策问题的决策矩阵为

(3)

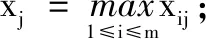
利用标准化矩阵求得各参数的关联系数：

(4)

式中：ρ∈[0,1]，本节取ρ=0.5，得到关联矩阵为

(5)

运用熵理论按如下步骤得到评估属性：

(1) 根据标准化矩阵R，第j个指标参数输出的熵可表示为

(6)

式中:K=(lnm)-1，由0≤Rij≤1可得0≤-∑Rij·lnRij≤lnm，指标参数输出的熵取值为：0≤Ej≤1,j=1,2,…,n。

(2) 求偏差度：dj=1-Ej,j=1,2,…,n。

(3) 确定熵权系数：

(7)

得到各指标间的加权向量：

W=[w1,w2,…,wn]T

(8)

2 空空导弹协同制导效能评估

美国的AIM-120“先进中距空空导弹”(AMRAAM)是当今世界上最早进入现役的第四代主动雷达型空空导弹，AIM-120D是此系列中最新和最先进的型号。AMRAAM导弹在40余年的研制和改进过程中，沿着基本型、系列化的发展思路，吐故纳新、常改常新，在中距空空导弹领域一直保持着领先优势。AMRAAM导弹具有全天候、全方向、全高度作战和超视距攻击、发射后不管、多目标攻击、抗多种电子干扰等多种先进能力，赢得了国际上的广泛认可，不仅大量装备美国部队，还出口36个国家和地区。本文选择AMRAAM导弹系列中的主要型号，将其作为效能评估的对象，并使用所设计的协同制导算法计算其协同制导的相关参数，综合得出协同制导效能评估结果。

2.1 导弹主要性能参数

空空导弹制空作战的目标是击毁敌方的空中目标，其本身的性能参数是其发挥作用的主要决定因素。导弹的重量、包络、攻击距离、机动能力、脱靶量、制导时间等都在飞行和攻击目标的过程中起到重要作用，是代表导弹性能的重要指标参数，因此，在进行协同制导效能评估时选择它们作为分析的基础。表1列出了美国AMRAAM导弹主要性能参数。

表1 AMRAAM导弹主要性能参数Table 1 Main parameters of AMRAAM missiles

2.2 不同型号的效能评估结果

针对表1给出的同一系列、不同性能的导弹参数，采用基于信息熵的效能评估法进行权重计算与性能评估。结合1.2节中的式(3)～(8)进行计算和分析，不同型号的导弹参数权重值计算结果如表2所示。

表2 不同型号参数权重表Table 2 Weight table of different missile parameters

根据计算的权重值，进行导弹性能评估，结果如图2所示。在选择的导弹性能参数中，最大攻击距离、机动能力、战斗部重量、末制导距离的增大都有利于提高导弹性能，而受到载机平台的限制，导弹重量和包络则是越小越有利于提高导弹性能。本节所选取的评估法充分考虑了这一因素，从不同型号导弹不同参数的权重值计算可以反映这一点，详细情况见表2。导弹的综合效能指数随着型号的发展出现逐渐增大的趋势，这个分析结果也符合导弹发展现状。

图2 AIM-120系列空空导弹效能评估值Fig.2 AIM-120 missile effectiveness evaluation value

2.3 不同架构的协同制导效能仿真分析

多枚导弹协同攻击过程中，导弹之间存在着多种通信拓扑架构，不同的架构将会影响导弹的协同攻击效能。本节选取AIM-120D导弹的性能参数，设计了四种协同制导通信拓扑架构，使用1.1节中的制导律模型，计算在不同的架构下三枚导弹攻击一个机动目标的脱靶量和制导时间，并将其作为效能评估的依据，综合计算协同制导的效能指数。三枚导弹的具体通信拓扑如图3所示。

图3 导弹通信拓扑Fig.3 Missiles communication topology

导弹与导弹之间的具体通信拓扑架构如下：

(1) 通信架构a：三枚导弹两两通信实现全连接，导弹之间全通信，目标运动信息和导弹自身运动信息能够共享，每枚导弹根据最优制导律同时命中目标。通信拓扑矩阵表示为

(9)

(2) 通信架构b：导弹1分别与导弹2和导弹3进行通信，导弹2和导弹3之间无通信。弹目接近过程中，导弹2和导弹3将目标运动信息、自身运动信息以及导弹1的运动信息作为制导计算的参数，进行制导律计算，通信拓扑矩阵表示为

(10)

(3) 通信架构c：导弹2分别与导弹1和导弹3进行通信，导弹1和导弹3之间无通信。弹目接近过程中，导弹1和导弹3将目标运动信息、自身运动信息以及导弹2的运动信息作为制导计算的参数，进行制导律计算，因此通信拓扑矩阵表示为

(11)

(4) 通信架构d：导弹3分别与导弹1和导弹2进行通信，导弹1和导弹2之间无通信。弹目接近过程中，导弹1和导弹2将目标运动信息、自身运动信息以及导弹3的运动信息作为制导计算的参数，进行制导律计算，因此通信拓扑矩阵表示为

(12)

具体的协同作战场景为：目标初始位置位于(30，29) km，速度大小为500 m/s，初始弹道偏角为160°，以正弦形式的法向过载9sin(t/π)进行持续机动。三枚导弹从不同位置发射，导弹的初始发射状态如表3所示。

表3 导弹初始参数Table 3 Missile initial parameters

在上述仿真条件下，设导弹所能承受的最大法向过载uqmax=30g，最大切向过载urmax=10g，在导弹初始位置、目标初始位置、弹目相对距离、通信拓扑的共同影响下，将会使得式(2)中的制导模型参数ri，Uri，qi，Uqi影响协同攻击制导律进而形成不同的脱靶量和制导时间。仿真结果中不同通信架构的三枚导弹攻击同一目标，四种架构均能够在可接受大范围内同时命中目标，实现对高速大机动目标的协同打击。仿真结果如图4～6所示，由于四种架构的导弹飞行轨迹、弹目相对距离和剩余时间变化有相同的趋势，这里仅将架构a的仿真曲线结果列出。

图4 惯性系下弹目轨迹图Fig.4 Trajectoryofmissileandtargetininertialsystem图5 弹目相对距离变化 Fig.5 Changeofrelativedistancebetweenmissileandtarget图6 剩余时间变化Fig.6 Changeofremainingflighttime

将四种架构仿真计算结果中的脱靶量和制导时间列入表4和表5中，以此对比协同制导的精度和效果。四种架构中，三枚导弹均能够协同攻击命中目标。架构d的最大脱靶量为2.743 8 m，制导时间差为0.04 s，是四种架构中脱靶量和制导时间差最小的，由此表明架构d的协同制导效果最好。架构a的最大脱靶量和制导时间差次之，由于导弹之间处于全通信的架构下，网络的复杂性影响了协同制导的效果。架构b和架构c的形式，受到导弹的相对位置和目标机动的影响，协同制导效果相对受到影响，但是并没有影响到整体的多弹协同攻击毁伤效果。

表5 不同通信协议下制导时间对比Table 5 Guidance time comparison of different communication protocol

选取每种通信架构的最大脱靶量和最大时间差参数作为效能评估的参数值，与2.2节中的导弹参数一起构成评估参数，使用1.2节中的熵算法对参数权重进行计算，最大脱靶量和最大时间差的权重值如表6所示。

表6 不同架构参数权重表Table 6 Weight table of different architecture parameters

根据计算的权重值，进行导弹性能评估，结果如图7所示，表明架构d的协同制导效能最高。

图7 不同架构的协同制导效能评估值Fig.7 Results of cooperative guidance effectiveness evaluation

3 结 论

多枚空空导弹通过协同制导律，采用不同的弹道形式，完成攻击空中目标的制空作战任务，能够丰富作战样式，提高作战效能。导弹的效能首先取决于空空导弹本身的性能参数，多枚空空导弹以什么样的编队架构形式协同作战，也影响着整体作战效能。本文选取了国外先进空空导弹的代表型号，以典型作战场景为实例，设计了协同制导律，进而在信息熵评估法的基础上，考虑多枚导弹协同制导脱靶量、制导时间和导弹编队架构，分析了多弹协同的综合效能指数，分析结果符合现有空空导弹发展趋势。下一步还将扩展分析研究，细化导弹参数指标，将代表导弹空间作战能力的探测角度等指标参数引入评估方法，进一步提高评估的客观性和有效性。