基于差分进化算法的线性自抗扰控制参数优化

周 涛

(洛阳师范学院 物理与电子信息学院，河南 洛阳 471934)

0 引 言

通常，自抗扰控制(ADRC)分为线性自抗扰控制(LADRC)和非线性自抗扰控制。自抗扰控制具有响应速度快、鲁棒性好，精度高等优点，有较高的工程应用价值，已在运动控制、火力发电、化工、航空、飞行器控制等领域得到应用[1]，但经典的非线性自抗扰控制器参数数量较多，整定困难。目前，自抗扰控制参数整定问题已成为一个研究热点。Gao将线性自抗扰控制参数对应为控制器带宽ωc、观测器带宽ω0以及参数b，减少了整定参数的数量[2]。

自抗扰控制在各类光电稳定平台、导弹导引头、舵机等航空武器中得到广泛应用[3-6]。激光半主动导引头是各型激光制导导弹的核心部件，文献[4]采用自抗扰控制算法，对导引头内外部扰动进行总体估计并给予相应补偿，使导引头视轴的振动得以隔离，从而实现视轴的相对稳定及高精度控制。文献[5]基于导弹舵机系统的特点，结合误差分段PID响应速度快和自抗扰复合控制抗扰动好的优点，进行位置环控制。文献[6]采用基于自抗扰控制技术的平台惯导系统初始自对准方案。

对于不同的控制对象，控制系统的模型和扰动作用差别很大，目前，主要根据经验进行线性自抗扰控制参数整定，缺乏实用有效的自动整定方法，增加了线性自抗扰控制应用的难度，影响系统的抗扰性能和精度。因此，需要适用于不同类型控制对象的线性自抗扰控制参数自动优化方法。

文献[7]利用极点配置，提出了一种具有时变参数的扩张状态观测器。文献[8]利用粒子群优化算法对非线性自抗扰控制参数进行整定，但是运算较复杂。文献[9]利用BP 神经网络在线调整扩张状态观测器(ESO)的3个参数，并将自适应ESO 嵌入到非线性ADRC。文献[10]提出LADRC参数的工程配置方法，并应用于某高精度武器控制系统。文献[11]利用内模控制的方法对线性ADRC的带宽参数进行调整。文献[12]提出了一种基于动态响应过程时序数据挖掘的参数自整定算法，用于整定线性自抗扰控制器中误差反馈律的参数。文献[13]提出了一种通用二阶LADRC参数整定方法，适用于泛化线性过程，但其整定过程较繁琐。文献[14]采用递推最小二乘法对LADRC中的参数b进行辨识。

综上，线性自抗扰控制工程应用越来越广泛，但是，对于系统存在大幅值的复杂扰动量以及参数b不准确情况下， 目前还没有理想的自动整定线性自抗扰控制参数的方法，仍主要根据经验进行反复试凑，调试困难、周期长，影响了自抗扰控制的推广应用。因此，研究通用、高效的线性自抗扰控制参数自动优化方法，具有重要的工程应用价值。

目前，利用智能算法的参数整定普遍存在结构和运算复杂、效率和收敛精度低等缺点。本文提出采用差分进化算法自动优化线性自抗扰控制器的两个参数ω0和ωc。首先，论文研究二阶线性自抗扰控制的设计，分析差分进化算法的原理。为了提高算法的收敛速度、效率和精度，对差分进化算法参数设定进行分析，并利用该算法优化自抗扰控制两个带宽参数的整定。最后，针对存在大幅值总扰动量的二阶系统，在参数b准确和不准确的两种情况下，通过大量仿真实验，以验证差分进化算法参数整定的有效性。

1 二阶线性自抗扰控制的设计

1.1 三阶线性扩张状态观测器的设计

对于二阶系统，有

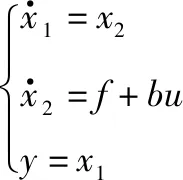
(1)

式中：x1，x2为系统的状态变量;参数b>0;u为系统实际控制输入量;y为系统输出;f为系统总扰动量，且有界，其可以是未知的线性或者非线性函数。

设计式(1)系统对应的三阶线性扩张状态观测器为

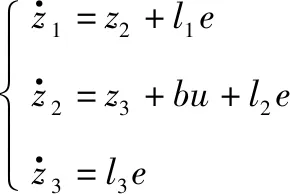
(2)

式中：l1>0，l2>0，l3>0，误差e=y-z1。

经过参数化，可以把ESO特征方程的极点配置在同一个位置-ω0处，即要求观测器的增益满足：

s3+l1s2+l2s+l3=(s+ω0)3

(3)

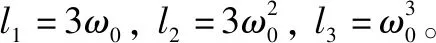
适当调整参数ω0，可使z1→y，z2→x2，z3→f，即状态z3可以准确估计系统总扰动量f。

1.2 反馈控制律的设计

若式(1)系统的设定输入为信号r，取控制输入量为

u0=kp(r1-z1)+kd(r2-z2)

(4)

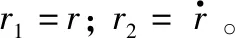
经参数化，可以把闭环误差系统特征方程的极点配置在同一个位置-ωc处，要求反馈控制律的增益满足：

s2+kds+kp=(s+ωc)2

(5)

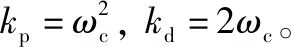
(6)

取式(1)二阶系统的实际控制输入量u为

(7)

适当地调节ωc，可使二阶闭环系统收敛，即x1→r1，x2→r2，且快速无超调。

因此，线性ADRC共需要整定三个参数：ω0，ωc和b。参数b对ESO的性能影响较大，不合理的取值会导致ESO发散，进而影响自抗扰控制系统的稳定性。参数b具有明确的物理含义，对于实际的二阶系统来说，可通过理论计算和实验验证的方法近似得到。通常，在许多实际工程应用场合中，参数b不能准确得到，只能取近似的估计值。因此，在进行参数b不准确的二阶系统自抗扰控制的情况下，增加了参数整定的难度。

大量实验证明，ω0和ωc两个参数的值互相耦合，它们的取值都影响线性自抗扰控制系统的稳定性和精度。同时，当系统存在大幅值的扰动量以及参数b不准确的情况下，对ω0和ωc两个参数的整定带来较大影响，使得整定过程变得更加困难。目前，还没有实用的自动优化这两个参数的方法，需要根据经验反复试错。以下提出利用差分进化算法进行ω0和ωc两个参数的自动优化。

2 差分进化算法

2.1 差分进化算法的原理

差分进化算法是一种随机启发式搜索算法，通过群体内个体间的合作与竞争产生的群体智能引导优化搜索过程。与神经网络、遗传算法等智能优化算法相比，该算法的主要优点是[15]：待定参数少，不易陷入局部最优，收敛速度快。

与遗传算法相比，它保留了基于种群的全局搜索策略，采用实数编码、差分形式的简单变异操作和一对一的竞争生存策略，降低了遗传操作的复杂性；同时，它利用特有的记忆能力动态跟踪当前的搜索情况，以调整其搜索策略，具有较强的全局搜索能力和鲁棒性[16]。仿真实验结果表明，对于同一个优化对象和相同的优化精度而言，与遗传算法相比，差分进化算法的种群大小和进化代数都较小，且运行时间较短[16]。

差分进化算法由变异、交叉和选择三个基本运算构成。

(1) 变异

从某一随机产生的初始群体开始，通过把种群中任意两个个体的向量差加权后按一定的规则与第三个个体求和，来产生变异新个体。

(2) 交叉

先设定交叉概率值，通过随机产生的一个概率数与设定交叉概率值比较，当随机概率数小于该值时，引入变异新个体；反之，保留初始目标向量。

(3) 选择

将一组变异新个体与当代种群中的某个预先得到的一组个体相比较，如果新个体组的适应度函数值优于与之相比较的个体组的适应度函数值，则在下一代中用变异新个体取代旧个体，否则，旧个体仍保留下来。

通过不断地迭代运算，保留优良个体，淘汰劣质个体，从而引导搜索过程向最优解逼近。

2.2 差分进化算法的步骤

差分进化算法主要包括4个步骤[15]：

(1) 生成初始群体

在n维空间里，随机产生满足约束条件的M个个体，具体运算如下：

(8)

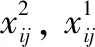
(2) 变异运算

从群体中随机选择3个个体xc1，xc2和xc3，i≠c1≠c2≠c3，且c1，c2和c3为随机整数，则变异运算为

hij(t+1)=xc1j(t)+L·[xc2j(t)-xc3j(t)]

(9)

式中：hij(t+1)为变异新个体；t为进化的代数；L为缩放系数；xc2j(t)-xc3j(t)定义为差异化向量个体，c1，c2和c3表示个体在种群中的序号。

(3) 交叉运算

交叉运算是为了增加种群的多样性，具体运算如下：

(10)

式中：vij(t+1)为实验向量个体；xij(t)为目标向量个体；lij为区间[0,1]的随机小数；Pcr为交叉概率，Pcr∈[0,1]。

(4) 选择运算

为了确定xi(t)能否成为下一代的成员，分别计算取n个实验向量vi(t+1)和目标向量xi(t)对应的适应度函数J的值，并进行比较：

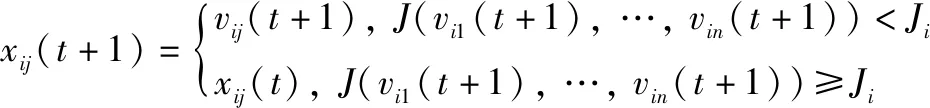
(11)

式中：Ji=J(xi1(t),…,xin(t))；n为变量的维度，对应于参数优化的数量。

反复执行步骤(2)～(4)，达到最大的进化代数G。

差分进化算法流程图如图1所示。适应度子函数流程图如图2所示。图中，N为采样点数量。

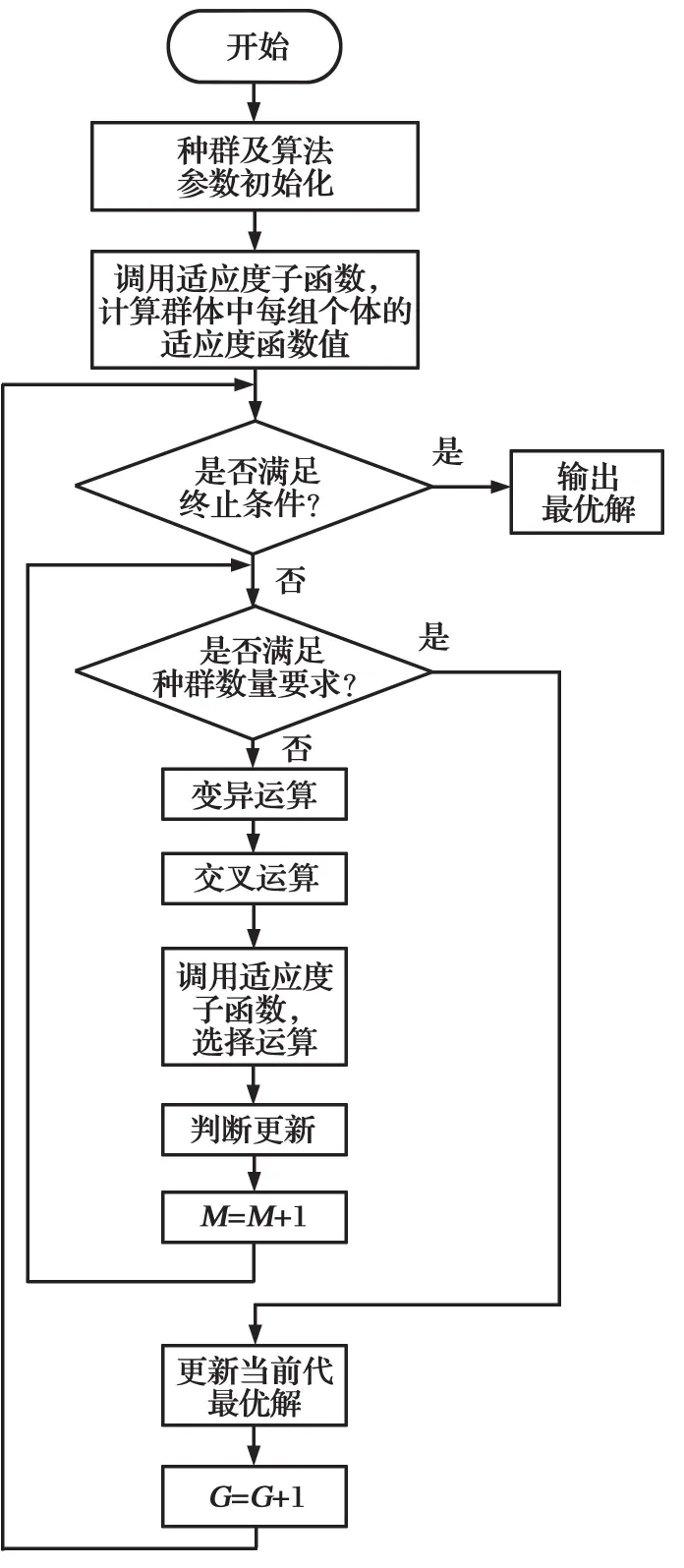
图1 差分进化算法流程图Fig.1 Flow chart of differential evolution algorithm

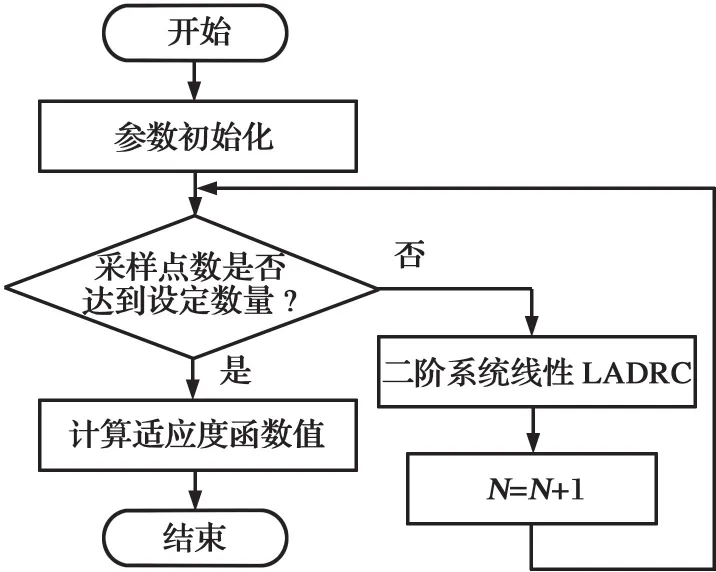
图2 适应度子函数流程图Fig.2 Flow chart of fitness subfunction

因此，可将上述二阶LADRC的两个参数ω0和ωc作为差分进化算法自动整定优化的对象。

3 仿真实验

采用差分进化算法对LADRC的两个参数进行优化仿真实验。设二阶系统为

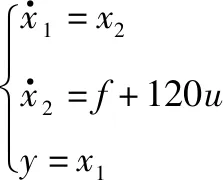
(12)

在式(12)二阶系统的模型中，参数b=120。假设系统总扰动量为

f=120[1.0sin(t(k))+x1x2+

sgn(sin(2t(k)))]-25x2

(13)

式中：t(k)为采样时间；sgn(sin(2t(k)))为符号函数。系统的总扰动量包括外扰f1和内扰f2，即f=f1+f2。其中f1=120[1.0sin(t(k))+sgn(sin(2t(k)))]为外部扰动，f2=120x1x2-25x2为内部扰动。系统总扰动量f为复杂非线性函数，因此，式(12)二阶系统为非线性系统。

如果式(12)二阶系统的设定输入为单位阶跃信号，则其稳态的输出值为x1=1，与二阶系统稳态的输出值x1相比，内扰和外扰的幅值都很大。

为了提高收敛速度和搜索精度，选取变异因子为

L=(Lmax-Lmin)·(G-t)/G+Lmin

(14)

式中：t为当前的进化代数；G为最大进化代数；Lmax为选择的变异因子最大值；Lmin为变异因子最小值。这样，在算法运行的初始阶段，L的取值较大，可以扩大搜索空间，保持种群的多样性。在收敛运行的后期，L的取值较小，实现在收敛的最优空间附近进行优化。

选取交叉因子为

Pcr=(Pcrmax-Pcrmin)·t/G+Pcrmin

(15)

式中：Pcrmax为交叉因子最大值；Pcrmin为交叉因子最小值。随着进化代数的增加，Pcr取值的增加，可提高收敛速度。

取适应度函数为

(16)

式中：w为系数；t(k)为采样时间；e2(k)=r(k)-z1(k)，为系统设定输入与输出的误差。根据需要适应度函数也可以采用其他形式。仿真实验结果表明，对于包含误差e2(k)的不同形式的适应度函数，差分进化算法优化结果的一致性较高。

群体个数M的值会影响算法获取最优解的概率。M的值越大，耗时越长，群体的多样性越好，取得最优解的概率越大。最大进化代数G越大，计算的最优解精度越高。一般选取L∈[0,3]。

设定LADRC两个参数的取值范围分别为：ω0∈[1，500]，ωc∈[1，800]。取差分进化算法的参数为：优化变量的维度n=2，最大进化代数G=50，群体个数M=50，Lmax=2，Lmin=0.1，Pcrmax=0.9，Pcrmin=0.6，w=0.6，采样点数量N=10 001。

3.1 b准确时的仿真实验

假设式(12)二阶系统的参数b精确已知，即取b=120。经过差分进化算法的优化，得到自抗扰控制系统参数的最优解为：ω0=468.657 8，ωc= 727.904 9，此时的适应度函数值为J= 0.370 8。当b=120时，系统阶跃跟踪响应曲线如图3所示，系统控制输入信号如图4所示，系统的扰动和估计如图5所示，适应度函数值的变化如图6所示。 图3表明，经参数优化后， 系统的跟踪精度高，响应速度快。图4表明，系统的控制输入量较小。图5表明，当参数b准确时，ESO的扰动估计精度高，并且扰动量的最大幅值接近300，远大于系统的稳态输出值。图6表明，适应度函数值快速达到最小值。

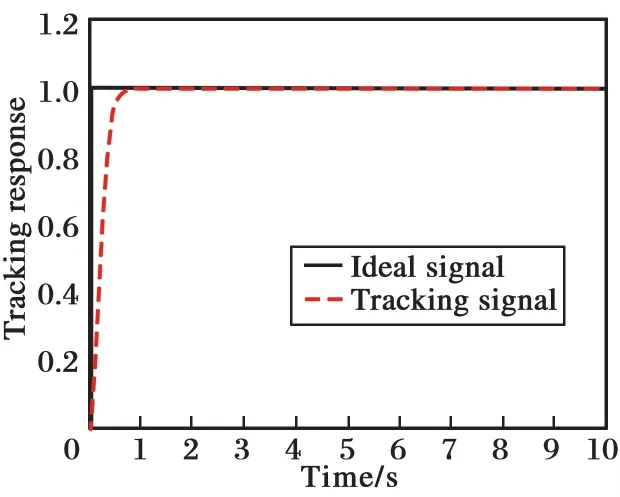
图3 系统阶跃跟踪响应曲线(b=120)Fig.3 System step tracking response curve(b=120)

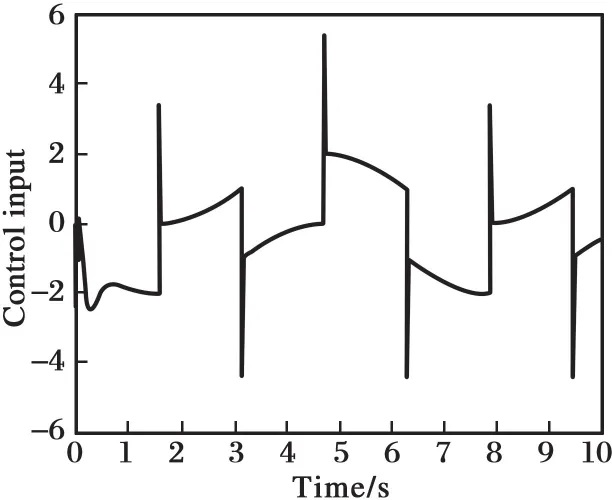
图4 系统的控制输入信号(b=120)Fig.4 System control input signal(b=120)

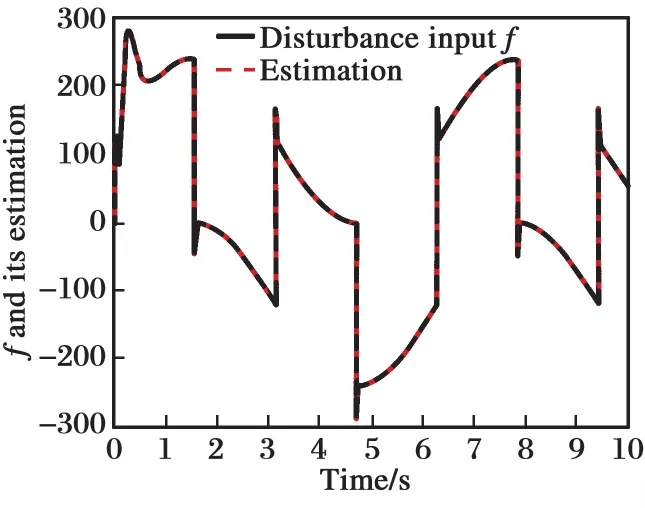
图5 系统的扰动和估计(b=120)Fig.5 System disturbance and estimation(b=120)

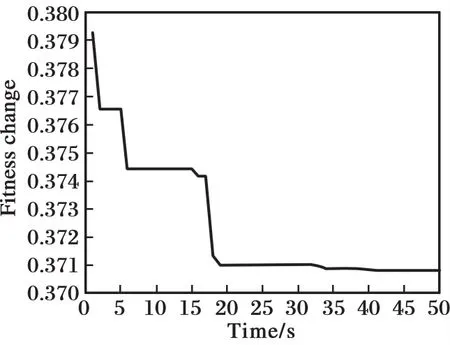
图6 适应度函数值的变化(b=120)Fig.6 Fitness function change(b=120)

因此，当b准确时，通过差分进化算法，可取得ω0和ωc两个参数全局的最优值，并且收敛速度快。

3.2 b不准确时的仿真实验

假设系统的参数b无法精确得到，当其估计值比b的真实值大50%时，即b=180，通过经验法调整两个参数ω0和ωc，很容易使系统发散，调整出理想数值的难度较大。

经过差分进化算法的优化，得到系统的最优解为：ω0=411.041 0，ωc=635.140 5，此时的适应度函数值为J=0.962 6。当b=180时，系统阶跃跟踪响应曲线如图7所示，系统控制输入信号如图8所示，系统的扰动和估计如图9所示，适应度函数值的变化如图10所示。

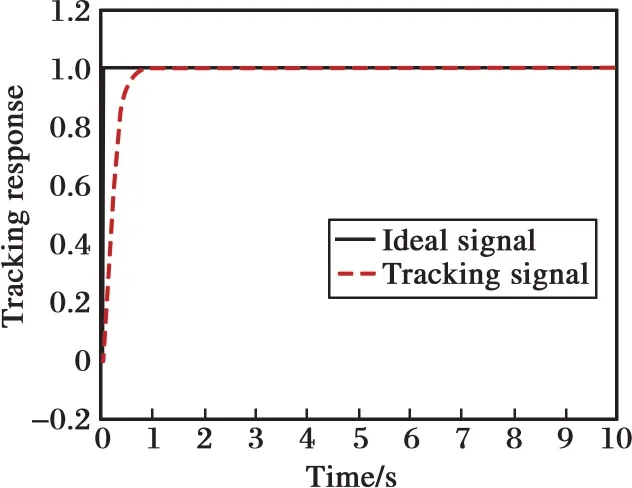
图7 系统阶跃跟踪响应曲线(b=180)Fig.7 System step tracking response curve(b=180)

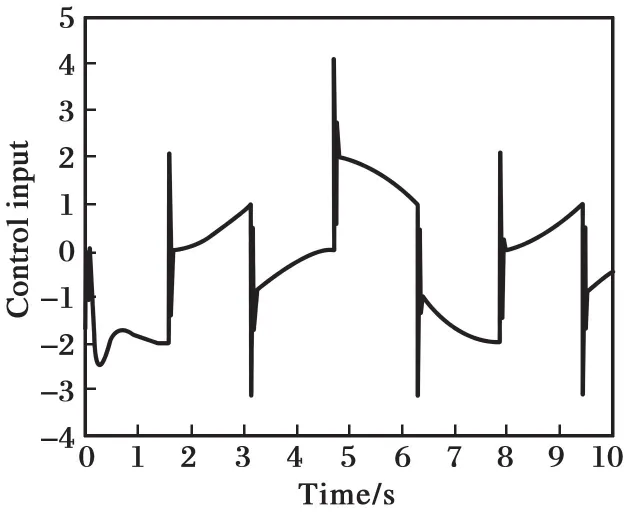
图8 系统的控制输入信号(b=180)Fig.8 System control input signal(b=180)

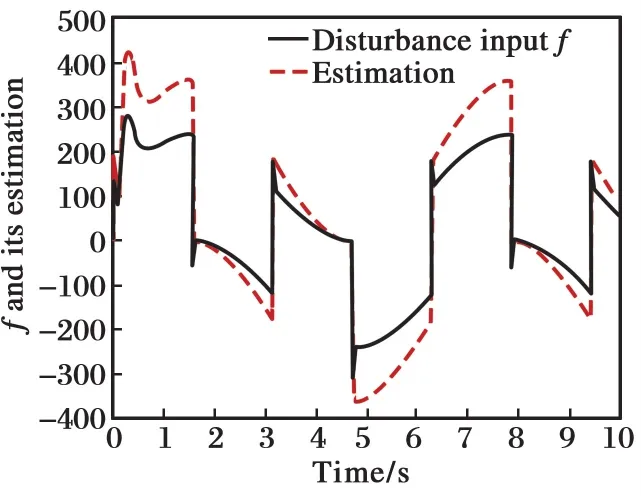
图9 系统的扰动和估计(b=180)Fig.9 System disturbance and estimation(b=180)

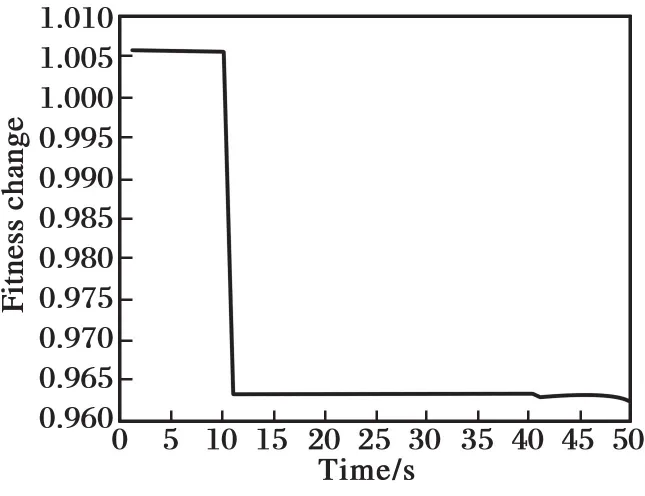
图10 适应度函数值的变化(b=180)Fig.10 Fitness function change(b=180)

图7表明，经参数优化后，系统的跟踪精度仍较高，响应速度快。图8表明，系统的控制输入量也较小。图9表明，由于参数b对ESO性能的影响，当参数b不准确时，ESO的扰动估计精度出现一定的偏差,并且扰动量的最大幅值接近300，远大于系统的稳态输出值。图10表明，适应度函数值也快速达到最小值。

此外，仿真实验表明，当参数b的估计值比其真实值小时，差分进化算法也能取得两个参数全局的最优解，同时适应度函数值快速达到最小值。

因此，当b不准确时，通过差分进化算法，也可取得两个参数全局的最优解，收敛的速度很快。

4 结 论

本文提出了采用差分进化算法自动优化线性自抗扰控制两个参数ω0和ωc，对于存在大扰动量的二阶非线性系统，在参数b准确和不准确的两种情况下，该差分进化算法均能取得两个参数全局的最优解，同时适应度函数值快速达到对应的最小值，从而实现了较高的系统阶跃响应速度和跟踪精度。对于三阶以上的高阶线性自抗扰控制系统参数优化问题，在修改算法的相关参数后，该差分进化算法同样适用。该算法收敛速度快，效率和精度高，具有重要的工程应用价值。