一种抗机翼挠曲变形的速度+姿态匹配快速对准算法

程海彬，鲁 浩，王进达

(1.中国空空导弹研究院，河南 洛阳 471009；2.航空制导武器航空科技重点实验室，河南 洛阳 471009)

0 引 言

机载战术导弹的中制导一般采用中低精度捷联惯导系统(SINS)，无法采用自对准方式进行初始化。弹载惯导相对于飞机惯导，姿态受飞机飞行条件、外挂公差、外挂结构、机翼燃料载荷变化以及机翼挠曲变形的影响，很难做出准确的瞬时计算，所以该类型弹载惯导的初始化都是采用传递对准。

常用的传递对准算法有速度匹配、速度+姿态匹配等，其中速度匹配算法应用最为广泛。速度匹配算法优点突出：计算量小，机翼扰动能力强，估计精度高，数值平稳度好。缺点也明显：一般平飞滤波收敛时间长度10 s左右，需要飞机做S机动才能获得航向失准角的估计。这会导致机头指向出现较大变化，在实际战术飞行中飞机不太可能做这样的机动，所以导致航向失准角通常无法估计。

为了解决这个问题，速度+姿态[1-2]、速度+角速度[3]等能够无需S机动的匹配方法得到了快速发展。文献[1]介绍了一种17阶状态方程的速度+姿态匹配传递对准算法，在F-16战机上的试验结果表明该算法能够在5 s内对准精度达到1 mrad(约3.44′)以内，这个结果是在公开文献上可见的战斗机上实测中所取得的最好结果。速度+姿态匹配算法相对速度匹配来说具有对准速度快(5 s内) 、精度高、对载机机动要求小(摇翼机动)等特点，但是姿态匹配算法易受到机翼挠曲变形、振动的影响，出现滤波稳定性、估计精度变差等问题。

为了提高速度+姿态匹配算法抗机翼挠曲变形的能力，解决失准角估计精度变低的问题，文献[4-5]采用扩充变量的方法，即对机翼进行建模扩充为状态变量，以提升失准角的估计精度，该方法显著增加计算量，同时估计精度完全依赖于机翼模型准确与否，一种武器需要装备多种飞机，挂装不同挂点，这就导致该方法在实际工程应用中存在较大局限；文献[6]采取规避的方法，采用速度+航向角方法削减机翼挠曲变形对失准角估计的影响，提升估计精度，该方法放弃了姿态匹配对俯仰和滚动失准角的估计，对航向失准角估计的快速性也大打折扣，无法真正发挥姿态匹配算法的快速性优势；文献[7]利用鲁棒性滤波的方法改善姿态匹配算法在机翼挠曲变形等动态干扰情况下的精度，该方法采用次优滤波提升极端干扰情况下算法精度，牺牲了正常情况下滤波精度。

本文考虑从频域入手，分析机翼挠曲与人为操作之间频率上的差异，寻找解决方法，即对姿态观测量进行预处理，从频域上抑制机翼等环节带来的高频挠曲对姿态匹配算法的影响，降低振动噪声对滤波精度的影响，在保持算法快速性与精度的前提下，使算法更具有工程应用价值。

1 系统误差方程

给出地球固联坐标系的惯导系统误差模型，工程上杆臂与时间误差均可精确补偿，不考虑文献[8]的处理方式，不作为状态变量进行估计，速度误差模型为

(1)

姿态误差模型为

(2)

器件常值误差模型为

(3)

εb=0

(4)

式中：δvn为速度误差；φ为平台失准角；Δb为加速度计零位偏置；εb为陀螺常值漂移；wa为加速度计噪声；wg陀螺噪声。

2 观测方程

2.1 速度观测方程

(5)

观测量：

(6)

式中：σv为速度量测噪声。

2.2 姿态观测方程

采用姿态余弦矩阵方法推导姿态观测方程，令

(7)

忽略二阶小项后：

(8)

将ZDCM转换为旋转矢量Zφ，可得观测量与状态变量间的关系为

(9)

式中：σφ为姿态量测噪声。

2.3 状态方程

为了减少计算量，将速度与姿态观测方程分开，先进行速度滤波，再进行姿态滤波：

Zv=HvX+σv

(10)

Zφ=HφX+σφ

(11)

2.4 速度+姿态匹配算法面临的问题

在传统速度匹配算法基础上引入姿态匹配，获得两种匹配方法各自优点的同时，也需要面对组合后的算法在机翼挠曲变形、振动等恶劣的飞行条件下造成滤波精度变低的问题。

选取一次真实飞行试验数据，对该次试验弹载惯导陀螺测量值以及姿态观测量进行频谱分析，确定真实飞行环境下机翼挠曲变形以及武器挂架等环节所造成的影响。

该飞机采用平台式惯导，正常对准情况下导航误差不大于1 kn；子惯导陀螺零位漂移不大于10 (°)/h，加速度计零位偏置不大于0.001g。飞机为东向平飞状态，噪声水平属于偏大范围。频谱分析结果如图1所示。从频谱中可以看出：数据在8 Hz，15 Hz，26 Hz以及35 Hz附近存在峰值，这说明飞行过程中机翼与挂架在该频率点存在谐振，对滚动轴X影响最重。

图1 陀螺输出以及频谱Fig.1 Gyro output and frequency spectrum

为了证明该变化不是飞机整体运动所致，对该组数据计算的姿态观测量Zφ进行频谱分析；如果是飞机整体运动导致，主子惯导会同时测量到，该运动将在计算姿态观测量时被消除，将不会在姿态观测量中再次表现出来，频谱分析结果如图2所示。

图2 姿态观测量与频谱Fig.2 Attitude measurement and frequency spectrum

从图中可见，在量测值Zφ上同样出现了与陀螺频谱分析近似的谐振点，这说明不是飞机整体运动所致，而是只有子惯导测量到该量；姿态量测抖动的峰峰值高达1.4°，有用信号完全淹没在噪声中，这将对姿态匹配算法的估计精度与滤波平稳性产生非常不利的影响。

3 问题分析与解决

在飞机的实际飞行过程中，由人为控制引入的运动都为低频运动，即使最快的机动方式如摇翼机动，频率也不会超过3 Hz。因此考虑利用频率差异，在姿态匹配量测值的预处理上引入低通滤波器，以消除机翼挠曲和挂架振动的影响，从而提高滤波精度。

3.1 低通滤波算法的选择

数字滤波器[9-10]可分为无限脉冲响应数字滤波器IIR和有限长单位冲激响应滤波FIR。IIR数字滤波器是一种递归的滤波，相位特性不好，在一些对相位特性要求较为严格的情况下不适用。FIR数字滤波器是一种非递归系统，最大的优点是容易设计成线性相位特性，而且不存在稳定性问题。但是对于同样的滤波器设计指标，FIR滤波器所需要的阶数比IIR滤波器高5～10倍，计算量大得多。本文选择巴特沃斯低通滤波器作为滤波算法，该算法具有通带内最大的平滑度。

3.2 巴特沃斯低通滤波算法设计

IIR数字滤波器的差分方程可以描述为

(12)

借助MATLAB所提供的信号处理能力完成IIR滤波器的设计[5-6]。滤波器设计要求效果越好，所需的阶次则越高，高阶次的滤波器有两方面的问题：

(1) 高阶次的滤波器计算量剧增，纯软件实现数字滤波器使得计算负担加重；

(2) 阶次越高的滤波器导致的相位延迟越大，这给后续Kalman滤波带来负面影响，相位延迟影响滤波的快速性，同时会导致失准角估计出现稳态偏差。

考虑到实测数据频谱分析最低为8 Hz振动频率，为了进行高、低阶次滤波器对比仿真，滤波器参数选择如下：

(1) 通带截止频率：4 Hz;

(2) 阻带截止频率：14/10 Hz;

(3) 通带衰减限制(最大值)：2 dB;

(4) 阻带衰减范围(最小值)：30/40 dB。

根据以上参数获得滤波器阶数为4阶与7阶，该滤波器的幅频特性如图3所示，给出4阶滤波器系数如下：

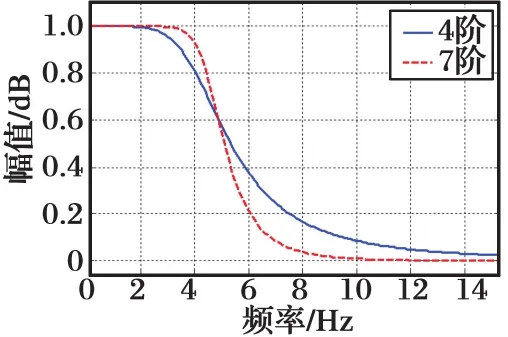
图3 幅频特性曲线Fig.3 Amplitude frequency curves

a={1 -2.338 4 1.878 -0.512 9}

b={0 0.014 8 0.011 8 0}

4 仿 真

4.1 仿真条件

根据文献[11]以及速度+姿态匹配算法特点，仿真轨迹设定如下：速度250 m/s，北向飞行，其轨迹姿态变化如图4所示。0～2 s平飞，2～6 s摇翼一次，6 s之后维持平飞状态。

图4 姿态角Fig.4 Attitude angle

偏航、俯仰、滚转失准角为15′，20′，25′；陀螺与加速度计常值误差为1 (°)/h，0.000 5g；滤波周期96 ms。

机翼挠曲模型：幅值为X轴0.6°、Y轴和Z轴0.3°、频率8 Hz的正弦信号，引入扰动模型前、后的姿态观测量如图5所示，可见引入扰动后，有用信号完全淹没在噪声中。

图5 姿态观测量对比Fig.5 Comparison of attitude measurement

对引入扰动信号的观测量再进行频谱分析，如图6所示，可以得到与实测数据相似的频谱特性。

图6 加入扰动后姿态观测量频谱Fig.6 Attitude measurement spectrum after adding disturbance

4.2 对比仿真

(1) 速度+航向与速度+姿态匹配对比仿真

两种匹配算法对比仿真结果如图7所示，可见在该飞行轨迹的激励下，速度+姿态匹配算法5 s内可以收敛至3′以下，远优于单纯速度匹配算法；同时优于速度+航向角匹配算法，速度+航向角匹配算法能够加快航向失准角的估计，但效果并不理想，20 s估计误差刚刚达到5′以内。同时，可以见到姿态匹配的引入，也加快了俯仰失准角的估计收敛速度。

图7 失准角估计误差Fig.7 Estimation error of misalignment angle

(2) 加入机翼挠曲模型仿真

将机翼挠曲模型带入仿真，仿真结果如图8所示。挠曲与振动导致速度+姿态匹配算法在滤波的前10 s三个方向失准角估计值均出现大幅抖动，抖动值超过10′，说明在较强机翼扰动干扰下，姿态匹配算法受到了严重影响，从而导致整体估计精度降低。

图8 扰动情况下失准角估计误差Fig.8 Estimation error of misalignment angle under disturbance

(3) 引入低通滤波预处理算法后仿真

首先对姿态观测量Zφ利用所设计的4阶巴特沃斯低通滤波器进行预处理；预处理前、后姿态观测量如图9所示，处理后的观测量噪声幅值明显降低。

图9 低通滤波情况下姿态观测量Fig.9 Attitude measurement under low-pass filter

使用经过低通滤波后的观测量进行速度+姿态匹配算法的Kalman滤波，失准角滤波估计结果如图10所示。结果表明，引入低通滤波后，速度+姿态匹配算法能够在严重机翼扰动干扰下稳定工作，滤波结果远好于一般速度+姿态匹配算法在该环境下的表现；滤波5 s后失准角估计精度可以达到3′以内，估计精度与无机翼挠曲情况下相当，估计精度略有降低，偏差1′以内。

图10 低通滤波预处理后失准角估计误差Fig.10 Estimation error of misalignment angle after low-pass filtering preprocessing

(4) 不同阶次低通滤波器对滤波估计的影响

低通滤波器幅频特性越好，滤波器阶数越高，带来的滤波稳定性越高；但是阶数越高，导致的延迟越大，带来更大的稳态误差。对前文所设计的4阶与7阶低通滤波器进行对比仿真，如图11所示。可见低通滤波器阶数越高，带来的稳态偏差越大。所以在滤波阶数上选择上，不应该片面追求平稳性。

图11 航向失准角估计误差Fig.11 Estimation error of heading misalignment angle

5 结 论

本文给出了地球固联坐标系下速度+姿态匹配快速传递对准算法。为了解决姿态匹配算法在恶劣挂载环境下失准角估计精度下降问题，采取了一种在频域上解决该问题的新方法，即通过低通滤波预处理的方法，削弱姿态量测中机翼挠曲高频影响，保留低频人为机动信息。该方法实现简单，计算量小，能有效提高恶劣环境下算法的估计精度。经过全面的对比仿真，结果表明引入巴特沃斯低通滤波后的速度+姿态匹配算法可以在恶劣的机翼形变与振动环境中保持稳定工作，方法有效，解决了算法对机翼挠曲变形与振动敏感的问题，拓展了算法的适用范围。