螺旋桨对无人作战飞机电磁散射特性影响

刘战合，苗 楠，王 菁，杨 涛，张 芦

(郑州航空工业管理学院 航空工程学院，郑州 450046)

0 引 言

随着武器系统的逐步升级，无人机作战系统开始成为现代战争中举足轻重的武装力量[1-3]，对于局部战争和反恐战争，固定翼无人机已参战多年，并取得了诸多战术成果。中、大型固定翼无人机已逐步从单一的侦察、探测过渡到察打一体型[4-5]，如美军攻击型无人机“捕食者”、“死神”及对地攻击机X-47B和X-47C等。采用飞翼布局的X-47B等无人攻击机具有较好的隐身性能，其布局电磁散射特性已有较多的研究，而对“捕食者”或“死神”之类的无人作战飞机来说，电磁散射特性研究较少，尤其是采用螺旋桨推进的无人作战飞机。

对无人机来说，与其他类飞行器相似，隐身技术是提高其战场生存力的重要措施[6-8]，一般通过采用主动或被动的设计技术或改进措施,降低被敌方雷达探测、识别、确认的信号，进一步降低目标被探测到的可能性[9]。飞行器隐身性能在很大程度上取决于外形隐身设计，与机翼、机身、垂尾等设计有较大关系，对其电磁散射特性研究较多。相对而言，采用螺旋桨推进时(如美国“捕食者”和“死神”等)，无人机的电磁散射特性将产生较大变化。为研究其影响规律和散射特性，从整机角度出发，提出了有、无螺旋桨两种模型方法研究螺旋桨对无人机电磁散射的影响。本文以美军“死神”无人机为基础，建立了其电磁散射分析模型，基于物理光学法(PO,Physical Optics)[10-11]计算了不同频率、不同俯仰角下的雷达散射截面(RCS，Radar Cross Section)曲线，分析了重点角域内RCS均值的变化特点，并基于RCS相对差值，研究了螺旋桨对电磁散射特性的量化影响关系，为攻击型无人机的隐身性能预估提供技术参考。

1 电磁散射分析模型

参考美军“死神”无人机，为研究螺旋桨对分析目标的散射影响，分别建立了有桨、无桨的电磁散射分析模型，对应命名为A和B模型，如图1所示。该模型几何尺寸为：机身长10 m，翼展14 m，高3 m，采用二者模型相互对比方法(暂未考虑模型A的螺旋桨旋转影响)，来分析螺旋桨对无人机电磁散射特性的影响。

图1 无人机电磁计算模型Fig.1 Electromagnetic computation models of UAV

以螺旋桨推进的无人战斗机具有较低的飞行速度、较高的机动性，适于执行空中打击、格斗、侦察的作战任务。一般地，该类无人机具有较高的升阻比，采用大展弦比矩形机翼实现较远航程和较长的航时需求，同时为改善隐身性能，双垂尾一般会斜置(即“V”形设置)。在执行作战任务中，面临敌方的雷达等探测器、防空导弹、侦察机(有人或无人)、战斗机等的探测、识别及攻击威胁。

基于以上考虑，从该类无人机面临的主要威胁方式出发，研究螺旋桨在相应环境下对无人机的电磁散射特性影响。考虑实际情况，电磁波入射俯仰角设定为-15°～15°，步长为5°，方位角为0°～360°，频率设置为1，3，6，10，15，18 GHz，分别对应电大尺寸为46.7，140，280，466.7，700，840，属于高频散射区域。同时，对无人机来说，重点关注的威胁角域：前向30°(定义为H-30，即前向±15°范围)、侧向30°(定义为S-30，即侧向90°左右两侧±15°范围)、后向30°(定义为T-30，即后向180°左右两侧±15°范围)、周向360°(W-360)等不同角域。研究中，结合模型A和B的RCS曲线分布特性、算术均值及其相对差值的变化规律等分析螺旋桨对该无人机的电磁散射影响特性。

2 电磁散射特性影响分析方法

2.1 电磁散射计算方法

在以上研究频率内，两种电磁散射分析模型均可视为电大尺寸计算目标，结合计算精度和效率需求，RCS计算方法可采用高效数值方法或高频近似方法[12-13]。高效数值方法主要为数值方法的快速计算策略，如基于矩量法(MOM，Method of Moments)的多层快速多极子算法(MLFMA，Multilevel Fast Multipole Algorithm)[14-15]、时域有限差分法(FDTD,Finite Difference Time Domain)[16]、有限元法等，为进一步提高效率，可采用并行计算技术，如并行多层快速多极子算法(PMLFMA,Parallel Multilevel Fast Multipole Algorithm)。对于电大尺寸复杂目标，即便采用高效数值方法也存在效率降低的现象，甚至计算过程不能收敛。为解决以上问题，可采用高频近似算法，如物理光学法(PO)、物理绕射理论、等效电磁流法、一致绕射理论等。物理光学法忽略了多层快速多极子算法中的远距、近距耦合散射作用，仅考虑影响最为明显的自耦合作用，从而大大提高计算速度，同时不存在收敛问题，这一近似处理尤其适用于如本文目标的光滑表面目标，具有较高的计算精度。利用物理光学法[10-11]，计算目标的RCS可由式(1)求和而得:

(1)

式中：σi为第i个面元的复RCS，可采用切平面近似来求解[10]。为验证物理光学法计算精度，以柱高1 m、直角边长为1 m的等腰直角三角形柱为例，分别采用PO和MLFMA计算了入射电磁波波长为0.1 m、俯仰角为0°、方位角为0°～180°的RCS曲线。两种方法计算结果对比如图2所示，其中MLFMA计算结果为水平极化情况。

图2 三角形柱RCS计算结果对比Fig.2 RCS comparison results of triangular column

从图2可以看出，采用MLFMA和PO两种算法得到的计算曲线基本重合，散射曲线分布特点相同，说明在0°～180°方位角上，二者计算结果基本一致，算术均值误差为0.863 5 dB，说明两种算法具有接近一致的计算精度，可用于电大尺寸飞行器目标的电磁散射特性数值研究。

2.2 螺旋桨电磁散射影响分析方法

对飞行器而言，一般通过研究RCS散射曲线的分布规律来研究该类飞行器的电磁散射特性。为了解RCS散射幅值量化变化规律，可结合不同角域内的RCS几何均值或算术均值大小来辅助研究。以上常规方法在一定程度上可以反映飞行器的电磁散射规律，但对于飞行器上的不同结构目标，如外挂、垂尾等部件，其散射特性影响仅能通过理论关系进行判断，缺乏可以量化分析的手段。

为进一步分析无人机螺旋桨的影响规律及其姿态角、频率影响特性，针对电磁散射分析模型A和B，结合已有方法，对重要威胁角域，通过对比两种电磁散射模型的RCS均值，获得螺旋桨对无人机电磁散射的影响特性。

在重点关注角域内，无人机RCS(单位为dBsm)算术均值可以表示为

(2)

式中：N为RCS数据的采样点数目；σi为第i个入射角时无人机的RCS。定义螺旋桨对该类无人机RCS影响的相对差值为

(3)

3 无人机电磁模型RCS分布特性

3.1 不同频率

为研究两种无人机模型的RCS曲线分布特性，分别从不同频率、不同俯仰角两方面研究其变化规律。由于统一模型各频率电磁散射曲线分布特性相似，选取0°俯仰角下10 GHz和18 GHz时两模型的RCS曲线进行对比，分析研究频率影响特性，如图3所示。

图3 两种模型不同频率的RCS曲线(10 GHz和18 GHz)Fig.3 RCS curves of two models with different frequency (10 GHz和18 GHz)

对两种模型而言，计算频率均处于高频区，图3说明，两种模型的RCS曲线分布具有较大区别。对模型A，频率10 GHz和18 GHz时RCS曲线基本接近，曲线分布规律一致。可以看出，为提高推力性能，螺旋桨桨叶在设计过程中有一定扭转，同时与前向有一定夹角，受此影响，模型A的RCS曲线并非完全对称。总体来看，在前向0°角域上有较大较宽波峰，是机身头部、机翼前缘、垂尾前缘，尤其是螺旋桨的电磁散射综合表现，最大为20 dBsm左右。方位角增加时，RCS逐渐降低，在30°时出现一较窄较小散射波峰，分析是头部侧棱和机身的散射耦合影响。侧向90°存在较大波峰，但其宽度较窄，主要是机身侧向、机翼翼尖面积的镜面散射作用及垂尾侧面的较弱散射作用。考虑到机身侧向采用翼身融合布局设计方式，机翼翼尖截面积较小，且垂尾已斜置，因此侧向波峰仅表现为较尖锐的散射波峰。在后向较大区域内，螺旋桨影响依然明显，130°附近有较小散射波峰，而在后向180°附近存在明显电磁散射波峰，为尾喷口端面、螺旋桨桨叶表面的镜面散射及机翼、垂尾后缘散射效果，其波峰宽度较大、强度较高、散射效果复杂。

对模型B，RCS散射曲线分布较为简单，沿周向对称分布四个波峰，分别在前向0°、侧向90°、后向180°、侧向270°附近。在前向0°上，散射波峰的最大幅值接近模型A，但表现更窄，在较大方位角上，散射幅值降低较为明显；在侧向90°上，由于螺旋桨侧向影响较小，因此散射波峰大小和宽度基本一致，说明散射机理并未明显变化；在后向180°上，两种模型的散射强度接近，但模型B的散射波峰宽度变小，且幅值在180°左右两端快速降低，这是由于模型B在后向无螺旋桨影响。

对比两种模型曲线可以看出，由于研究频率范围均处于高频区内，因此两个频率的RCS曲线区别不大，但通过RCS曲线对比，依然可以发现，频率增大时，散射曲线振荡更为剧烈，同时，幅值有一定降低，这一点模型B表现相对明显。同时，螺旋桨在无人机前向、后向均有明显影响，较大幅度、较大范围的增大了RCS幅值，尤其在前向H-60角域(即-30°～30°范围)内，增大幅值接近40 dB；在后向较大范围上也有明显影响。

3.2 不同俯仰角

入射频率10 GHz时，两种模型俯仰角0°和10°的RCS曲线对比如图4所示。

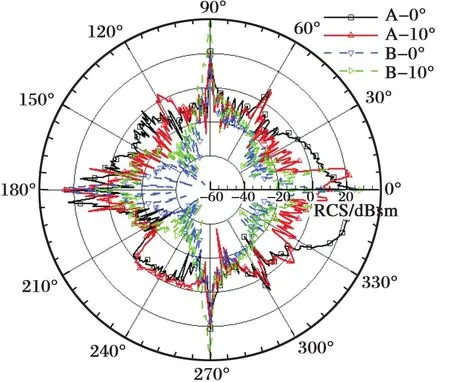
图4 两种模型不同俯仰角的RCS曲线(10 GHz)Fig.4 RCS curves of two models with different pitch angles (10 GHz)

由图4可以看出，同一入射频率下，俯仰角变化对RCS曲线影响较为复杂，表现不同。

对模型A，俯仰角增大时，RCS散射曲线在前向、后向较大范围均有明显降低，在前向H-60角域上表现更为明显，部分区域在10 dBsm以上，这是前向上螺旋桨桨叶表面的镜面散射减弱的表现。同时，俯仰角的变化也会对波峰位置有一定影响，如在前向0°方位角附近，波峰出现了偏转，俯仰角10°时约在6°方位角上出现了波峰，而其余部位降低较为明显。分析认为，这是由于螺旋桨的非对称和截面随桨叶径向产生扭转的共同结果。以上现象还表现在后向角域上，可以看出，俯仰角增加时，后向角域的RCS也有一定降低，但比前向影响幅值相对稍弱，为发动机尾喷口后端面和桨叶表面镜面散射降低的共同作用。在侧向一定角域范围内，对散射波峰的影响并不明显，这是由于俯仰角的变化对侧向散射并未引起实质的散射机理变化。

对模型B，散射曲线特点有所不同，由于缺少了螺旋桨的电磁散射贡献，在较小的俯仰角变化时，其散射幅值变化并不明显。在前向60°角域上，受无人机头部结构外形设计影响，俯仰角增加时，其RCS曲线变化不明显，仅有较小的增加，幅值在2 dB左右；在后向60°角域，由于无人机尾部结构较为复杂，俯仰角变化时，尾部复杂结构在入射方向形成一定的二面角效果，一定程度上增加电磁散射，其RCS曲线有较小增加。而在侧向90°附近，波峰大小、幅值均未明显变化，与模型A类似，该角域上，俯仰角变化并未引起散射机理的较大变化。综上，对模型B来说，较小的俯仰角并未引起RCS曲线分布的较大变化。

4 螺旋桨电磁散射影响规律

在RCS散射曲线分布特点的基础上，为研究螺旋桨对电磁散射的影响规律，分别计算分析了模型A、模型B的RCS均值及相对差值，并对不同频率、不同俯仰角的影响详细分析。

4.1 螺旋桨对RCS均值影响对比分析

在RCS数据基础上，分别计算了模型A和B的H-30，H-60，S-30，T-30和W-360角域的RCS均值，模型A和B各角域RCS均值分别如表1～2所示。结合RCS散射曲线分布特点及影响范围，分析时重点关注入射频率(f)变化时H-60和T-30角域的RCS均值情况。

表1 不同角域的RCS均值(模型A)Table 1 RCS arithmetic mean of different angular domains (model A)

表2 不同角域的RCS均值(模型B)Table 2 RCS arithmetic mean of different angular domains(model B)

从表1～2可以看出，频率增加时，除模型A在H-30和H-60角域上的RCS均值变化不大外，其余角域上随频率的增加明显降低，说明频率增加时该角域的隐身性能有一定提升，这一点也可从RCS散射曲线看出。

同时，在不同入射频率上，螺旋桨均对前向和后向角域的RCS均值有较大影响。对前向H-60角域，结合RCS散射曲线分析，频率增加时，螺旋桨对电磁散射的影响逐渐增加，1 GHz时由-13.948 7 dBsm增加至6.461 7 dBsm，而在18 GHz时由-27.392 7 dBsm增加至6.716 7 dBsm。对后向T-30角域来说，频率增加时，两种模型的RCS均值均降低，但频率较大时，这一差值更大，说明在高频时，螺旋桨影响较为明显，这与前向角域的结果一致。

4.2 不同频率电磁散射影响

俯仰角0°、入射频率1～18 GHz的螺旋桨对RCS影响的相对差值变化曲线如图5所示。

图5 不同频率相对差值变化曲线Fig.5 Curves of RCS relative values in different frequency

结合RCS曲线和均值变化，RCS相对差值可进一步量化研究螺旋桨对无人机电磁散射特性的影响。图5可以看出，各角域上的RCS相对差值变化不一，频率增加时，前向(H-30和H-60)角域的RCS相对差值振荡增加，由1 GHz的20.115 4 dB增加至18 GHz的35.449 3 dB，证明螺旋桨对前向两个角域上的电磁散射有重要影响，显著增强了电磁信号，降低了无人机隐身性能。结合RCS曲线可以看出，在前向和后向，RCS曲线由于螺旋桨作用，明显向外膨胀。对于后向T-30角域，螺旋桨带来的RCS增加部分淹没在无人机尾部后端面的复杂结构电磁散射中，结合RCS曲线，依然在除波峰之外的一定角域上有较大影响，从而促使后向T-30角域的相对差值大于零，与前向角域效果类似，也表现为振荡增加现象，但其幅值较低，从1 GHz的6.261 6 dB增加至11.220 6 dB。

对侧向来说，并未产生散射机理的明显变化，螺旋桨本身在侧向S-30角域内的影响较小，其RCS相对差值基本维持在3～5 dB之间。从图5可以看出，相对差值曲线基本不变。对周向W-360来说，由于该角域是0°～360°方位角上即各个角域上的综合表现，图5显示，周向相对差值随频率增加逐渐增加，且高于后向T-30角域，说明螺旋桨对周向电磁散射影响也较大，1 GHz时为15.424 8 dB，而18 GHz时为22.233 1 dB。

4.3 不同俯仰角电磁散射影响

入射频率10 GHz、俯仰角-15°～15°时螺旋桨对RCS影响的相对差值变化曲线如图6所示。

与上述不同频率电磁散射影响分析同理，螺旋桨在不同俯仰角上同样有较大影响，结合无人机作战实际情况，将俯仰角设定为-15°～15°范围。从图6可以看出，相对不同频率来说，不同俯仰角的RCS相对差值曲线变化有以下特点：(1)各个角域的RCS相对差值变化更加剧烈，即对俯仰角的响应更加敏感；(2)前向(H-30和H-60)角域上，呈现中间高两端低的特点，即在0°俯仰角附近较高，俯仰角增加或减小时有所降低，这与无人机结构及螺旋桨布局相关，尤其在前向H-30角域上呈“W”形分布；(3)侧向S-30、后向T-30角域上呈振荡变化趋势，S-30角域的相对差值振荡性减小，而T-30角域上在较大范围上变化。

图6 不同俯仰角相对差值变化曲线Fig.6 Curves of RCS relative values in different pitch angles

从螺旋桨对电磁散射的影响效果来看，前向H-30和H-60角域上影响最大，且0°俯仰角上的RCS相对差值为28 dB左右，为各角域上最大值。与H-30角域特点不同，H-60角域上的RCS相对差值随俯仰角变化成倒“V”形分布，二者俯仰角较大时差异较为明显。对后向T-30角域，受螺旋桨及无人机结构影响，RCS相对差值在-15°和-10°俯仰角时，分别为10.980 3 dB和11.445 5 dB，而在俯仰角-5°时最大，为25.774 5 dB，之后先降低再增大，表现为大范围的振荡现象。侧向S-30角域的RCS相对差值由-15°的16.956 8 dB快速振荡降低到15°俯仰角的2.173 8 dB。周向W-360角域上，相对差值-5°最大，两侧降低，而俯仰角为正时降低较快。

总体来看，螺旋桨会增加各个角域上的电磁散射强度，频率、俯仰角变化时，前向H-30和H-60角域影响较大，增加幅值为20～40 dB，后向T-30角域影响次之，增加幅值为4～20 dB，侧向S-30影响最小，对10 GHz来说，增加幅值可达28.804 3 dB，从而较大地降低了无人机的隐身能力。基于以上考虑，有必要在不降低其推进效率、结构强度、气动特性等性能的基础上，采用技术手段大幅降低螺旋桨的电磁散射影响，如螺旋桨采用非金属材料、对桨叶进行气动隐身优化设计、优化桨叶气动扭转角、保证推力的同时适当增加桨叶后掠角等。同时，鉴于螺旋桨在实际作战中为转动部件，应进一步研究其所带来的频响效应。

5 结 论

为研究螺旋桨对攻击型无人机的电磁散射影响特性，建立了某型无人机电磁散射分析模型，基于物理光学法计算分析了有、无螺旋桨的无人机模型RCS曲线，提出了分析螺旋桨的电磁散射研究方法，研究了螺旋桨对RCS曲线分布规律的影响，及不同频率、不同俯仰角的电磁散射影响特性，得到以下结论：

(1) 对RCS曲线影响。螺旋桨对RCS曲线有显著影响，会明显增加无人机前向、后向较大范围内的RCS幅值，并使散射曲线向外膨胀，前向、后向散射波峰幅值和宽度均大幅增加，前向表现尤为明显，且螺旋桨使周向散射波峰数目更多，侧向散射机理发生实质变化。

(2) 不同频率影响。在高频区，频率增加时不会引起电磁散射机理变化，RCS散射曲线分布形式基本相似；频率增加会引起前向、后向角域的RCS均值降低(模型A的H-60除外)，前向、后向、周向的RCS相对差值随频率增加而振荡增加，前向H-30角域最明显，可达35.449 3 dB。

(3) 不同俯仰角影响。螺旋桨结构设计特点使模型A的电磁散射特性随俯仰角增加而变小，RCS曲线向内一定程度收敛；俯仰角变化时，螺旋桨对前向角域(H-30和H-60)RCS相对差值影响较大，前向H-30角域呈“W”分布，且俯仰角0°时RCS相对差值最大，为28 dB左右，后向T-30角域RCS相对差值大范围震荡变化，各向角域相对差值均大于零。