基于演化博弈论的秸秆压块服务站建设分析及利润分配

王冬计，李 营，刘联胜，刘春雨，贾思琪，董奇烜

(1.河北工业大学 能源与环境工程学院，天津 300401；2.河北工业大学 经济管理学院，天津 300401)

北方农村地区燃煤采暖造成严重的环境污染，对居民身体健康产生严重威胁[1]。为营造舒适、清洁的居住环境，急需推广清洁采暖方式。秸秆具有低灰、低硫、低氮、CO2零排放等优点[2-3]，用秸秆压块燃料替代散煤取暖已成为解决能源问题和改善生态环境的有效途径之一[4]。然而，传统的秸秆直燃方式因存在燃料收集与使用劳动强度高、堆放占用空间大等问题，而被逐渐富裕起来的农民舍弃。采用成型技术将松散的秸秆(60～80 kg/m3)压缩为压块燃料(700～1 300 kg/m3)既便于运输、存储，又可以有效提高燃料的能量密度[5]，使其便于使用，用于农村采暖不仅可以减少化石燃料消耗，还可减少温室气体排放，是一条可行的可持续发展道路[6-8]。

目前，中国的秸秆压块燃料供应链多呈“农户→秸秆经纪人→压块生产企业→燃料市场”的模式。秸秆被农民低价出售给秸秆经纪人，经多级秸秆经纪人后由压块生产企业收购，成型后的产品在燃料市场出售。该供应链属于单向多层的服务模式，成型燃料因多次利润叠加而价格高昂，致使农民使用压块燃料的意愿较弱，形成了农民仅供应秸秆原料而不使用压块产品的开环结构，供需两侧的物质与价格均不稳定。造成该现象的主要原因是对农户的行为模式认识不够准确，将农户行为模式认为是典型的经济人。实质上，农民既是秸秆供应者又是压块燃料消费者。在农村地区构建秸秆压块服务站公共服务设施，形成“农户→秸秆压块服务站→农户”，则可去除供应链的中间环节，构建稳定可靠的区域能源市场体系，实现以可再生能源替代散煤供暖，进而达到节能减排的效果。

秸秆压块服务站在组织关系上涉及到当地政府、企业和农民三部分，三者不是孤立的个体而是互利共赢的合作者。研究三方参与主体的行为策略是一个典型的博弈问题，解决博弈问题一直存在很多方法，如静态博弈、动态博弈、重复博弈等[9]。但以上博弈理论沿袭经典经济学的完全理性人假设[10]，即政府、企业和农民均被视为完全理性人，在一次博弈或重复博弈中即可找到最佳策略。然而这一假设与实际是不相符的。实际情况下各参与主体的知识、能力及智慧等方面是不同且有限的，而且仅仅通过简单的重复博弈是不能使所有参与主体达到“共同知识”的[11]。秸秆压块服务站建设博弈过程，不仅涉及农民、企业及政府各主体客观的经济行为，还存在农民和企业可能不知道其他参与主体收益函数的情况，并且各主体都有各自的习惯和经验，存在系统推理误差等主观因素。政府、企业及农民都是有限理性人，且三方之间的博弈是一个信息不完全的复杂动态博弈过程。演化博弈论认为人的理性是有限的，不要求完全信息条件，它强调一种动态均衡[12]。为此选取演化博弈理论对秸秆压块服务站建设问题进行研究。

首先构建政府、企业及农民三方博弈模型；其次，结合演化博弈稳定性理论寻找三方博弈的稳定点，讨论不同条件下模型的稳定状态，分析各参与主体的行为策略；然后采用Shapley值法建立利润分配模型；最后结合案例对政府的激励和三方利润分配占比进行量化分析，以期为政府制定合理的激励策略提供理论支持。

1 演化博弈模型的构建

演化博弈理论包括复制动态方程[13]和演化稳定策略[14]两方面内容。前者强调的是选择，后者强调的是变异。复制动态方程是描述博弈方的某一特定策略在一个种群中被采用频数的动态微分方程。演化稳定策略是指在多方博弈过程中，由于博弈方都是有限理性的，不可能在起初就找到各自最优策略，博弈方需对有利策略不断修正和改进，直至趋于某个稳定策略。

1.1 模型假设与参数

秸秆压块服务站的建设由政府、企业和农民三方群体组成。通过分析各群体行为，构建三方演绎博弈模型。在三方博弈中，政府以社会效益和环境效益最大化为决策依据；企业以自身利益最大化为决策依据；农民以自身受益最大化为决策依据。政府的决策为采取经济激励政策或不采取经济激励政策，企业的决策为投资建设秸秆压块服务站或不投资建设秸秆压块服务站，农民的决策为采用秸秆压块取暖或不采用秸秆压块取暖。基于上述参与主体的决策行为，做出如下假设。

假设1：政府、企业和农民之间的博弈属于不完全信息博弈，即三方掌握的信息均不完全。

假设2：农民不采用秸秆压块取暖所带来的环境损失，在政府采取经济激励政策、企业建设情况下，政府和企业共同承担该项损失，其中政府承担比例为β，企业承担比例为1-β；其余情况下政府承担该项损失。

各参与主体的相关参数设定如下：

政府采取经济激励政策需付出的成本记为C1，万元；政府不采取经济激励政策需付出的宣传成本记为C2，万元。其他参与主体均积极参与下政府获得的社会效益和环境效益记为R1，万元；其中因企业的积极参与政府获取的效益比例为θ；其他参与主体均不参与下政府的损失记为D1，万元。

企业投资建设秸秆压块服务站付出成本记为C3，万元；获得的经济效益记为R2，万元；获得的政府补贴记为W1，万元。企业不建设秸秆压块服务站损失的社会声誉记为C4，万元。

农民采用秸秆压块取暖需付出燃料成本记为C5，万元；获得的政府补贴记为W2，万元。农民不采用秸秆压块取暖需付出燃料成本记为C6，万元；造成的环境损失记为D2，万元。

1.2 模型建立

根据以上假设，构建图1所示的政府G、企业E和农民F之间的博弈树模型。图中yes代表主体的行为是参与秸秆压块服务站的建设和使用，no代表主体的行为是不参与秸秆压块服务站的建设和使用。数字1、2、3、4、5、6、7、8分别代表不同的情况，如数字1表示政府采取经济激励政策、企业投资建设秸秆成型燃料服务站、农民采用秸秆压块取暖的情况。

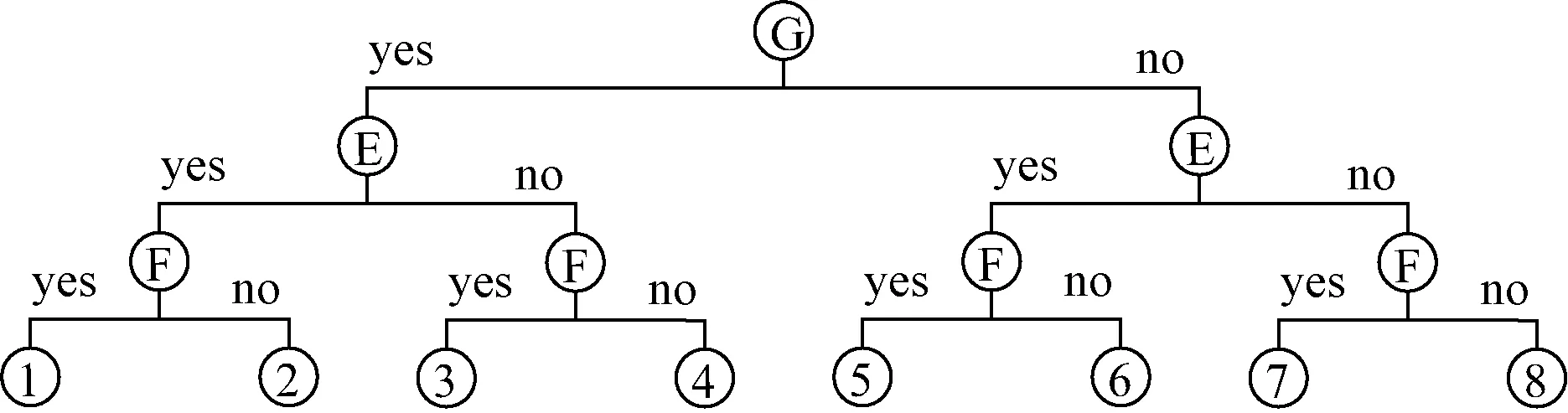
图1 政府、企业以及农民之间的博弈树模型

根据上述博弈树模型得出农民采用秸秆压块取暖与不采用秸秆压块取暖的收益情况分别如表1、表2所示。

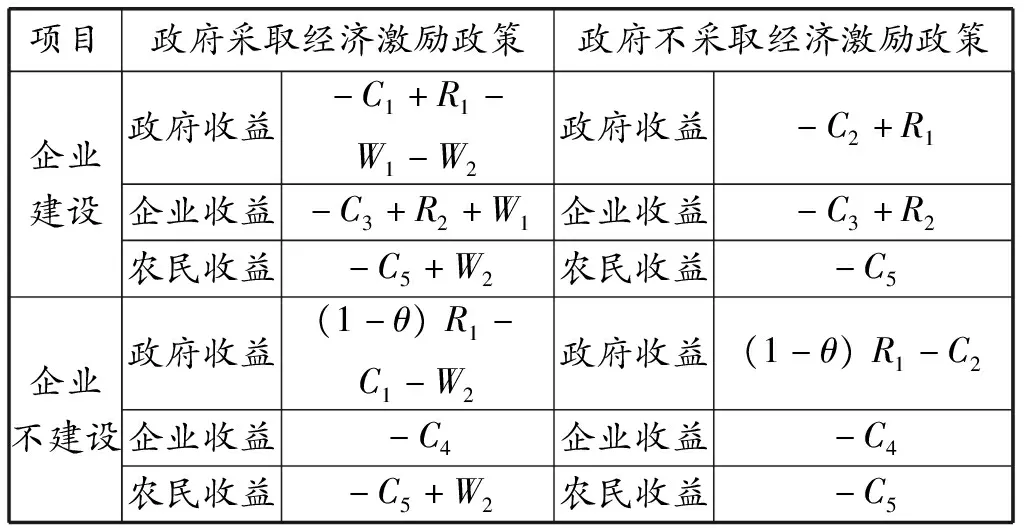
表1 农民采用秸秆压块取暖时各主体的收益情况

表2 农民不采用秸秆压块取暖时各主体收益情况

1.2.1 政府的博弈策略

设定政府采取经济激励政策的概率为x，则政府不采取经济激励政策的概率为1-x；企业投资建设秸秆压块燃料服务站的概率为y，则企业选择不投资建设秸秆压块燃料服务站的概率为1-y；农民采用秸秆压块取暖的概率为z，则农民不采用秸秆压块取暖的概率为1-z。政府、企业、农民的平均期望收益分别用H1、H2、H3表示。

政府的平均期望收益用式(1)进行计算，即

H1=xH11+(1-x)H12

(1)

式中H11、H12分别为政府采取经济激励政策的期望收益和政府不采取经济激励政策的期望收益，万元，分别由式(2)、式(3)进行计算，即

H11=yz(-C1+R1-W1-W2)+(1-y)z[(1-θ)R1-C1-W2]+y(1-z)(-C1+θR1-W1-βD2)+(1-y)(1-z)(-C1-D1-D2)=yz[-D1+(β-1)D2]+y[(1-β)D2+D1+θR1-W1]+z[(1-θ)R1+D1+D2-W2]+(-C1-D1-D2)

(2)

H12=yz(-C2+R1)+(1-y)z[(1-θ)R1-C2]+y(1-z)(-C2+θR1-D2)+(1-y)(1-z)(-C2-D2-D1)=z[(1-θ)R1+D1+D2]+y(θR1+D1)-yzD1+(-C2-D1-D2)

(3)

随着群体不断演化，群体中的个体不断选择某策略进行博弈，采用某策略的个体的期望收益高于群体平均收益，则该类个体的数量会增加；反之，则该类个体的数量会减少。这就表明在演化过程中群体中个体总数量一直处于不断变化中，而采取经济激励政策策略的个体概率也在不断变化，用于描述这个概率变化情况的方程即为复制动态方程。采用复制动态方程，即选择某一特定策略概率的变化等于该策略的收益值与群体平均收益值之间的差值[14-15]。基于此，政府采取经济激励政策策略的复制动态方程x′(t)由式(4)进行计算，即

x′(t)=x(H11-H1)

(4)

基于上述政府收益和复制动态方程，展开得到政府采取经济激励政策策略的概率x的复制动态方程为

(5)

1.2.2 企业的博弈策略

企业的平均期望收益由式(6)进行计算，即

H2=yH21+(1-y)H22

(6)

式中H21、H22分别为企业投资建设秸秆压块服务站和不投资建设秸秆压块服务站的期望收益，万元，分别由式(7)和式(8)进行计算，即

H21=xz(-C3+R2+W1)+(1-x)z(-C3+R2)+x(1-z)[-C3+R2+W1-(1-β)D2]+(1-x)(1-z)(-C3+R2)=x[W1-(1-β)D2]+xz(1-β)D2-C3+R2

(7)

H22=-C4

(8)

同理，企业采取建设策略的复制动态方程y′(t)由式(9)进行计算，即

y′(t)=y(H21-H2)

(9)

基于上述企业收益和复制动态方程，展开得到企业采取建设策略的概率y的复制动态方程为

(10)

1.2.3 农民的博弈策略

农民的平均期望收益由式(11)进行计算，即

H3=zH31+(1-z)H32

(11)

式中H31、H32为农民采用秸秆压块取暖和不采用秸秆压块取暖的期望收益，万元，分别由式(12)和式(13)进行计算，即

H31=xy(-C5+W2)+x(1-y)(-C5+W2)+(1-x)y(-C5)+(1-x)(1-y)(-C5)=xW2-C5

(12)

H32=xy(-C6)+x(1-y)(-C6)+(1-x)y(-C6)+(1-x)(1-y)(-C6)=-C6

(13)

同理，农民采取秸秆压块取暖策略的复制动态方程z′(t)由式(14)进行计算，即

z′(t)=z(H31-H3)

(14)

基于农民收益和复制动态方程，展开得到农民采取秸秆压块取暖策略的概率z的复制动态方程为

(15)

1.3 三方演化路径及稳定性分析

令F1(x)=0，F2(y)=0，F3(z)=0，可以得到8个平衡点，分别为S1=(0，0，0)，S2=(0，0，1)，S3=(0，1，0)，S4=(0，1，1)，S5=(1，0，0)，S6=(1，0，1)，S7=(1，1，0)，S8=(1，1，1)。除上述8个平衡点外，还存在平衡点S9=(x，y，z)，其中x、y、z均在区间(0,1)内。该平衡点的表达式为

(16)

根据式(16)求解得到平衡点S9=(x，y，z)，即

(17)

根据演化博弈的稳定性理论可得，若dF1(x)/dx<0，dF2(y)/dy<0，dF3(z)/dz<0，则S9=(x，y，z)为三方博弈的稳定点，其中

(18)

1.3.1 政府的演化稳定策略

1)当yz(β-1)D2-y[(1-β)D2-W1]-zW2-C1+C2=0，即y、z取式(17)中的数值时，表明x取任意值，系统都处于稳定状态，不再演化。此时政府既可以选择采取经济激励政策，也可以选择不采取经济激励政策。

2)当yz(β-1)D2-y[(1-β)D2-W1]-zW2-C1+C2<0时，dF1(0)/dx<0，dF1(1)/dx>0。依据微分方程稳定性判别条件，当F′(x)≤0时取得稳定，则可得x=0为演化稳定策略。表明政府逐渐从采取经济激励政策的策略向不采取经济激励政策的策略演化，即不采取经济激励政策是此时政府的演化稳定策略。

3)当yz(β-1)D2-y[(1-β)D2-W1]-zW2-C1+C2>0时，dF1(0)/dx>0，dF1(1)/dx<0。此时x=1为演化稳定策略，表明政府逐渐从不采取经济激励政策的策略向采取经济激励政策的策略演化，即采取经济激励政策是此时政府的演化稳定策略。

1.3.2 企业的演化稳定策略

1)当x[W1-(1-β)D2]+xz(1-β)D2-C3+R2-C4=0，即x，z取式(17)中的数值时，表明y取任意值，系统都处于稳定状态，不再演化。此时企业既可以选择投资建设秸秆压块服务站，也可以选择不投资建设秸秆压块服务站。

2)当x[W1-(1-β)D2]+xz(1-β)D2-C3+R2-C4<0时，dF2(0)/dy<0，dF2(1)/dy>0。此时y=0为演化稳定策略，表明企业逐渐从投资建设秸秆压块服务站的策略向不投资建设秸秆压块服务站的策略演化，即不投资建设秸秆成型燃料服务站是此时企业的演化稳定策略。

3)当x[W1-(1-β)D2]+xz(1-β)D2-C3+R2-C4>0时，dF2(0)/dy>0，dF2(1)/dy<0。此时y=1为演化稳定策略，表明企业逐渐从不投资建设秸秆压块服务站的策略向投资建设秸秆压块服务站的策略演化，即投资建设秸秆压块服务站是此时企业的演化稳定策略。

1.3.3 农民的演化稳定策略

1)当xW2-C5+C6=0，即x取式(17)中的数值时，表明z取任意值，系统都处于稳定状态，不再演化。此时农民既可以选择采用秸秆压块取暖，也可以选择不采用秸秆压块取暖。

2)当xW2-C5+C6<0时，dF3(0)/dz<0，dF3(1)/dz>0。此时z=0为演化稳定策略，表明农民逐渐从采用秸秆压块取暖的策略向不采用秸秆压块取暖的策略演化，即不采用秸秆压块取暖是此时农民的演化稳定策略。

3)当xW2-C5+C6>0时，dF3(0)/dz>0，dF3(1)/dz<0。此时z=1为演化稳定策略，表明农民逐渐从不采用秸秆压块取暖的策略向采用秸秆压块取暖的策略演化，即采用秸秆压块取暖是此时农民的演化稳定策略。

1.4 三方共同作用的演化策略稳定性分析

根据Ritzberger和Weibull[16]提出的结论，只需对S1=(0，0，0)，S2=(0，0，1)，S3=(0，1，0)，S4=(0，1，1)，S5=(1，0，0)，S6=(1，0，1)，S7=(1，1，0)，S8=(1，1，1)8个均衡点的稳定性进行分析。有学者提出应用雅可比矩阵的局部稳定性可得到均衡点的稳定性[17]。根据博弈三方的复制动态方程，可以得到如表3所示的雅可比矩阵。

表3 雅可比矩阵

由李亚普诺夫第一法则可知，演化稳定策略(ESS)对应的雅可比矩阵的特征根必须小于0[18]。各均衡点的特征根值如表4所示。

表4 各均衡点的特征根

主要关注服务站能够顺利建设和运行下各参与主体的策略行为，即主要关注S8=(1，1，1)点的稳定性。依据表4可知，S8=(1，1，1)点的特征根分别为C1-C2+W2-W1+2D2(β-1)，C4+C3-R2-W1，-C6+C5-W2。S8=(1，1，1)点为稳定点时，其特征根需要同时满足以下条件：

(19)

即当政府、企业及农民的付出成本和收益大小符合上述条件时，政府采取经济激励政策策略、企业采取建设策略、农民采取采用秸秆压块取暖策略的概率均为1。

2 模型分析

2.1 政府行为分析

依据式(17)可得政府采取经济激励政策的概率为x=(C5-C6)/W2。政府的策略选择取决于农民采用秸秆压块取暖需付出的燃料成本C5、农民不采用秸秆压块取暖需付出的燃料成本C6及政府给予农民的补贴W2。与农民采用秸秆压块取暖需付出的燃料成本C5成正比，与农民不采用秸秆压块取暖需付出的燃料成本C6和政府给予农民的政府补贴W2成反比。这表明农民采用秸秆压块取暖的成本越高，政府越需要加大经济激励力度，以提高农民的参与积极性。农民不采用秸秆压块取暖的成本越高，政府的经济激励力度可以相应减弱。

2.2 企业行为分析

2.3 农民行为分析

农民选择采用秸秆压块取暖的概率为z={W2(C3+C4-R2)-(C5-C6)[W1-(1-β)D2)]}/[(1-β)D2(C5-C6)]。当政府补贴W2=[(C5-C6)W1]/(C3+C4-R2)时，农民选择采用秸秆压块取暖的概率为1。通过政府补贴W2的表达式可看出政府对农民的补贴力度与农民采用秸秆压块取暖需付出的燃料成本C5成正比，与农民不采用秸秆压块取暖需付出的燃料成本C6成反比。这表明当采用秸秆压块取暖成本过高时，为了提高农民采用的积极性，政府需要加大对农民的补贴力度；当农民不采用秸秆压块取暖，仍采用燃煤取暖的成本越小时，农民对燃煤取暖的认可度越高，相应也就需要政府加大对农民采用秸秆压块取暖的补贴力度以促使农民放弃燃煤取暖。因此，政府可以通过限制煤炭使用量、调整煤炭价格、对超额燃烧煤炭的农民收取一定比例的惩罚费用等措施来提高农民燃煤成本，从而提高农民采用秸秆压块取暖的积极性。

3 利润分配

根据博弈局中人之间是否具有约束力的协议，可以将一个博弈过程分为合作博弈和非合作博弈。合作博弈主要研究在博弈局中人之间具有约束力的协议并使得整体利益最大时，各局中人如何分配收益的问题。其中，合作是合作博弈的基础，团体理性是其重点。根据前文政府、企业、农民三者之间的博弈模型，假设三者达成合作协议，进行合作博弈模型建立，得出三者的合理利益分配。

Shapley值法由Shapley于1953年提出，为解决多个局中人在合作过程中因利益分配而产生矛盾的问题，属于合作博弈领域。该方法是按照成员对联盟的边际贡献率将利益进行分配，即成员i所分得的利益等于该成员为其所参与联盟创造的边际利益的平均值。基于Shapley值进行联盟成员的利益分配避免了分配上的平均主义，比任何一种仅按资源投入价值、资源配置效率及将二者相结合的分配方式都更具合理性和公平性，也体现了各盟员相互博弈的过程[18-19]。因此，采用Shapley值法对政府、企业、农民博弈进行利润分配。

3.1 Shapley值法概述

3.1.1 符号定义

定义Shapley值法需用到的符号如下：

1)n、N：假设合作博弈中有n个博弈局中人，由N={1, 2, …,n}表示n个博弈局中人的集合。

2)S：不同博弈局中人组成不同的联盟，记为S，S是N的子集，N为总体联盟。

3)v(S)：定义在N上的一实函数v为特征函数，即联盟S的收益记为v(S)。特征函数v(S)具有超可加性，若联盟S1和S2没有交集，则S1和S2构成新联盟的利益大于等于联盟S1和S2的收益之和，即当S1、S2符合S1∩S2=Ø条件时，v(S1+S2)≥v(S1)+v(S2)。

4)xi(v)：表示联盟中成员i获得的利益。

3.1.2 Shapley值法

Shapley证明了Shapley值分配策略满足有效性公理、对称性公理、冗员性公理和可加性公理时，Shapley值是唯一的。4个公理的内容如下：

2)对称性。设π是N={1, 2, …,n}的一个排列，对于N的任意子集S={i1,i2,…,in}，有πS={πi1,πi2,…,πim}。若在定义特征函数w(S)=v(πS)，则对于每个成员i∈N都有xi(w)=xπi(v)。这表示合作获利的分配不随利益相关者的先后顺序或者记号标记变化。

3)冗员性。若对于包含成员i的所有子集S都有v(S{i})=v(S)，则xi(v)=0。其中S{i}为集合S去掉元素i后的集合。这说明如果一个成员对于任何他参与的合作联盟都没有贡献，则他不应当从全体合作中获利。

4)可加性。若在N上有两个特征函数v1、v2，则有x(v1+v2)=x(v1)+x(v2)。这表明有多种合作时，每种合作的利益分配方式与其他合作结果无关，总分配是两项的和。

成员i从总体利益v(N)所分配的利益由式(20)进行计算，即

(20)

式中：Si为N中包含成员i的所有子集形成的集合；|S|为联盟S所包含的成员数，成员i在参与S联盟时有(|S|-1)!种排序，而剩余(n-|S|)个成员的排序有(n-|S|)!种排序，[(|S|-1)!(n-|S|)!]/(n!)为成员i对于联盟整体所应分得利益的权重；Si}为从集合S中删除元素i后的集合，[v(S)-v(Si})]为成员i参与不同联盟S为自身参与联盟创造的边际贡献。

3.2 秸秆压块服务站合作的利益分配模型

3.2.1 构建利润分配模型

秸秆压块服务站的合作博弈模型中有3个局中人：政府、企业和农民，分别记为A、B、C，局中人的策略都是要么合作要么不合作。现考虑的是合作博弈，3个局中人在博弈前都签订协议，合作形成一个联盟，根据上述介绍的Shapley值法可以计算大联盟中每个局中人的利益。下面首先计算各联盟的利益情况。

1)当3个局中人相互独立，即Shapley值法中的S=1时，各博弈局中人的利益情况如下：

政府(A)单独采取经济激励政策获得收益为v(A)=(-C1-D1-D2)。

企业(B)单独选择建设服务站获得收益为v(B)=(-C3+R2)。

农民(C)单独选择采用秸秆压块取暖获得收益为v(C)=(-C5)。

2)当3个局中人两两合作，即Sharpley值法中的S=2时，各联盟的利益情况如下：

当政府(A)与企业(B)合作时，相当于政府采取经济激励政策，企业选择建设服务站，农民选择不采用秸秆压块取暖，此时两者形成联盟的利益为v(A,B)=(θR1+R2-D2-C1-C3)。

当政府(A)与农民(C)合作时，相当于政府采取经济激励政策，企业选择不建设服务站，农民选择采用秸秆压块取暖，此时两者形成联盟的利益为v(A,C)=(-C1-D1-C5)。

当企业(B)与农民(C)合作时，相当于政府不采取经济激励政策，企业选择建设服务站，农民选择采用秸秆压块取暖，此时两者形成联盟的利益为v(B,C)=(-C3+R2-C5)。

3)当3个局中人都参与合作形成大联盟，即Sharpley值法中的S=3时，联盟的利益情况如下：

当政府(A)、企业(B)与农民(C)均合作时，相当于政府采取经济激励政策，企业选择建设服务站，农民选择采用秸秆压块取暖，此时三者形成联盟的利益为v(A,B,C)=(R1+R2-C1-C3-C5)。

3.2.2 模型求解

根据式(20)以及各联盟的利益情况，可以计算联盟中各局中人的边际贡献。该合作博弈中共有3个局中人，联盟S中的人数依次取1、2、3，分别对应各局中人相互独立、两两合作以及形成统一大联盟时的利益情况。下面求解各局中人的边际贡献。

3.2.2.1 政府获利情况

政府(A)可以组成的联盟有4种情况：{A}、{A，B}、{A，C}、{A，B，C}。依据Shapley公式计算得到政府(A)各联盟概率值、利益情况及总利润情况，如表5所示。

表5 政府(A)的Shapley值

依据表5可得：政府(A)单独参与项目的概率为1/3，此时政府获利-C1-D1-D2；政府分别与企业、农民合作参与服务站建设项目的概率均为1/6，此时政府获利分别为θR1-D2-C1、-C1-D1；政府、企业、农民三方合作参与的概率为1/3，此时政府获利为R1-C1。

综上，政府总获利xA(v)= 1/6[(θ+2)R1-6C1-3D1-3D2]。

3.2.2.2 企业获利情况

企业(B)可以组成的联盟有4种情况：{B}、{A，B}，{B，C}，{A，B，C}。依据Shapley公式计算得到企业(B)各联盟概率值、利益情况及总利润情况，如表6所示。

表6 企业(B)的Shapley值

依据表6可得：企业(B)单独参与项目的概率为1/3，此时企业获利(-C3+R2)；企业分别与政府、农民合作参与服务站建设项目的概率均为1/6，此时企业获利分别为θR1+R2+D1-C3、-C3+R2；企业、政府、农民三方合作参与的概率为1/3，此时企业获利为R1+R2+D1-C3。

综上，企业总获利xB(v)=1/6[6R2+(θ+2)R1+3D1-6C3]。

3.2.2.3 农民获利情况

农民(C)可以组成的联盟有4种情况：{C}、{A，C}、{B，C}、{A，B，C}。依据Shapley公式计算得到农民(C)各联盟概率值、利益情况及总利润情况，如表7所示。

表7 农民(C)的Shapley值

依据表7可得：农民(C)单独参与项目的概率为1/3，此时农民获利-C5；农民分别与政府、企业合作参与服务站建设项目的概率均为1/6，此时农民获利分别为D2-C5、-C5；农民、企业、政府三方合作参与的概率为1/3，此时农民获利为(1-θ)R1+D2-C5。

综上，农民总获利xC(v)= 1/6[2(1-θ)R1+3D2-6C5]。

3.2.2.4 利润分配比例

得到3个局中人的边际贡献后，将其单位化即可得到每个局中人在大联盟中的利益分配比例。令xT(v)=xA(v)+xB(v)+xC(v)，则政府(A)应得的利益分配比例为xA(v)/xT(v)，企业(B)应得的利益分配比例为xB(v)/xT(v)，农民(C)应得的利益分配比例为xC(v)/xT(v)。

根据各局中人的Shapley值，可以得到各局中人的利益分配比例如下。

政府的利润分配比例wA由式(21)进行计算，即

(21)

企业的利润分配比例wB由式(22)进行计算。

(22)

农民的利润分配比例wC由式(23)进行计算。

(23)

4 案例

某企业计划投资建设秸秆成型燃料服务站，计划投入成本100万(建厂费50万，设备费30万，人工20万)。设定政府补贴期限为5年。由于该企业为工程建设企业，依据非居民所得税核定征收管理办法中第五条规定，从事承包工程作业、设计和咨询服务的成本利润率为15%～30%。假定该企业每年预计利润率为25%，即企业每年利润为25万，5年总利润额为125万元。企业不投资建设秸秆压块服务站，5年损失的社会声誉总共为5万元。农民若采用燃煤取暖，每年需要煤2 t，每吨800元，即年成本为0.16万元，5年总成本为0.8万元；若采用秸秆压块取暖，每年需要4 t，每吨150元，即年成本为0.06万元，5年总成本为0.3万元。农民不采用秸秆压块取暖每年所带来的环境损失为6万元，5年总成本为30万元，其中政府承担损失比例为2/3。政府年宣传成本为7万，5年总成本为35万元。政府推行经济激励政策付出的年成本为5万，5年总成本为25万元。政府获得的年社会效益和环境效益为企业收益的1.4倍，即政府的5年总收益为175万元，其中因企业的积极响应政府获取的效益比例为3/5。企业和农民均不参与项目下政府的年损失为8万元，5年的总成本为40万元。企业和农民均不参与时政府没有补贴支出。

依据企业和农民参与概率均为1时的政府补贴表达式，将上述数据代入计算得知，政府每年需补贴企业8.729 5万元，每年需补贴农民0.218 2万元，5年内政府补贴开支为44.738 5万元。同时，在秸秆压块服务站建设和运行过程中，企业和农民始终是利益相关者，双方的策略选择都受到政府政策的影响，同时农民的参与程度也会影响企业投资建设秸秆压块服务站的积极性。对于政府而言，其对双方的补贴比例应该控制在一定范围内，这样既可以提高双方参与积极性，又可以节省财务开支。若政府对双方的补贴比例失衡，一方面这可能会降低某一方的参与积极性，另一方面也会增加政府财政支出。因此，确定一个相对合理的补贴比例对秸秆成型燃料服务站的建设和运行起着至关重要的作用。确定政府对企业和农民的补贴比例范围在40∶1时双方参与积极性最高。

依据式(21)～式(23)，将上述数据代入计算得知，政府的利益分配占比为9.06%，企业的利益分配占比为69.17%，农民的利益分配占比为21.77%。

5 结论

通过构建政府、企业以及农民三方参与主体的演化博弈模型，分析了不同情况下三方参与主体的演化结果，并对三方参与主体的行为进行了分析，得出以下主要结论：

1)政府采取经济激励政策策略的概率受农民采用秸秆压块取暖需付出的燃料成本以及不采用秸秆压块取暖需付出的燃料成本的影响。与农民采用秸秆压块取暖需付出的燃料成本成正比关系，与农民不采用秸秆压块取暖需付出的燃料成本成反比关系。两种采暖方式的成本差距越大，政府越倾向于采取经济激励政策。

2)企业采取建设策略的概率取决于政府满足企业自身补贴需求的程度。当政府出台相关财政补贴政策完全满足企业补贴需求后，企业选择参与建设秸秆压块服务站的概率为1。同时研究表明，政府对企业的补贴力度与企业建设秸秆压块服务站需付出的建设成本成正比关系，与企业建设所得的经济效益以及企业不建设损失的社会声誉成反比关系。随着企业建设成本降低或不建设损失成本升高，其对政府补贴力度的要求也会相应降低。

3)农民采取用秸秆压块取暖策略的概率取决于政府满足农民自身补贴需求的程度。当政府出台相关财政补贴政策完全满足农民补贴需求后，农民选择采用秸秆压块取暖的概率为1。同时研究表明，政府对农民的补贴力度与农民采用秸秆压块取暖需付出的燃料成本成正比关系，与农民不采用秸秆压块取暖需付出的燃料成本成反比关系。随着农民采用秸秆压块取暖燃料成本的降低或农民不采用秸秆压块取暖燃料成本的升高，其对政府补贴力度的要求也会相应降低。

4)除政府补贴力度会影响企业和农民参与程度外，政府对企业和农民的补贴比例也影响着双方策略选择。一个合理的补贴比例在企业和农民均选择参与该项目中发挥着至关重要的作用。企业和农民作为项目实施的利益相关者，双方策略的选择会相互影响。政府补贴比例不合理会导致某一参与主体积极性降低，从而影响另一参与主体的策略选择。研究结果表明，当政府对企业和农民的补贴比例保持在40∶1时企业和农民均倾向于参与该项目。

5)在秸秆压块服务站建设运行项目中，政府从中分配的利润最少，其次是农民，企业分配利润最多。政府、企业、农民的利润分配占比分别为9.06%、69.17%、21.77%，该结论与实际相符。政府作为宏观调控机构，本身的关注点不在盈利，其主要承担的是社会责任。而企业恰恰相反，其作为营利机构关注的焦点为利润额。