基于随机森林的重要性测度指标体系*

宋述芳，何入洋

(西北工业大学 航空学院， 陕西 西安 710072)

随机森林(Random Forest, RF)是Breiman于2001年提出的一种统计学习理论方法[7]。首先，通过Bootstrap重采样技术从原始样本集中抽取多个训练样本集，然后再利用抽取的样本集建立相应的决策树，并组建随机森林。随机森林应用广泛，不仅可以处理分类、回归问题，对于降维也有很好的适用性。随机森林对异常值与噪音也有很好的容忍度，稳健性强，不容易出现过拟合，被Iverson誉为当前最好的算法之一[8]。现有的基于随机森林的重要测度指标主要有两种：基于Gini指数的平均不纯度减少指标(Mean Decrease Impurity, MDI)和基于袋外(Out-Of-Bag, OOB) 数据置换的平均精确率减少指标(Mean Decrease Accuracy, MDA)[9-11]。基于Gini指数的MDI指标对离散特征存在偏向性，且重要性分析结果与特征变量的选择顺序有关[12-13]。基于OOB数据置换的MDA指标则可以直接度量每个特征变量对模型精确率的影响程度，不存在偏向问题，应用广泛。此外，基于OOB数据置换的MDA指标求解过程与基于方差的全局灵敏度分析的单层Monte Carlo模拟法相似，可由此作为切入点寻找两者之间的关系。

本文通过比较基于方差的全局灵敏度指标和基于OOB数据置换的MDA指标的求解过程，寻找两者之间的关系，并进一步建立基于随机森林的重要测度指标体系，包括单变量测度指标、组变量测度指标等，可为后期复杂环境、高维小样本数据的重要性测度分析奠定基础。

1 基于方差的全局灵敏度指标

由Sobol′提出的基于方差的全局灵敏度指标能够反映输入变量在整个变化范围内对输出响应方差的影响程度。Sobol′指标不仅具有很强的模型通用性，而且还可对输入变量进行分组讨论以及量化输入变量之间的交互影响，因此在工程领域得到了广泛应用。ANOVA (analysis of variance)分解是方差灵敏度指标分析的基础[6]。

1.1 ANOVA分解

响应函数Y=g(X)存在唯一的ANOVA分解式为

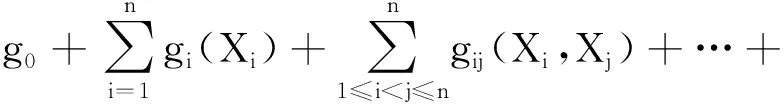
g1,…,n(X1,X2,…,Xn)

(1)

其中，常量g0为函数g(X)的期望值，gi(Xi)为单变量Xi的主效应分量。

(2)

式中，fXi(xi)为变量Xi的概率密度函数。

多个变量交互作用的分量可由下式求得

(3)

1.2 方差灵敏度指标

基于式(1)，分别对各分解项进行积分，由于各分解项正交，响应函数的方差V=VAR(Y)可以表示为各分解项的方差之和，即

(4)

其中，

(5)

用分解项的方差与响应函数的方差之比来衡量分解项的方差贡献率，即

Si1,…,is=Vi1,…,is/V

(6)

其中，Si表示单变量Xi的灵敏度主指标。

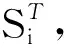
(7)

由概率论知识可知，基于方差的全局灵敏度指标可表示为[14-16]

(8)

(9)

其中，X～i表示除Xi外的所有变量组成的向量。

1.3 求解方差灵敏度指标的Monte Carlo法

采用传统的数字模拟法求解基于方差的全局灵敏度指标需要进行双层抽样，计算量大，不适用于复杂的工程问题分析[17]。单层Monte Carlo模拟法应用广泛，其求解步骤如下。

Step1:根据输入变量X的联合分布，抽取两组容量为N的样本，分别记为矩阵A和B：

Step2:将矩阵B中的第i列用A中的第i列代替，构造矩阵Ci：

Step3:计算输入变量Xi的方差灵敏度主指标和总指标，即

(10)

(11)

2 基于随机森林的重要性测度分析

随机森林是一种统计学习理论方法，利用Bootstrap重采样方法从数据库中抽取样本，并运用决策树对每组Bootstrap样本进行建模，组合多棵决策树，通过投票(分类)或取平均值(回归)得出最终的预测结果[7]。随机森林具有很高的预测精度，鲁棒性好，防止过拟合，在分类、回归、降维等问题中得到了广泛应用。基于随机森林的重要性测度指标有：基于Gini指数的MDI指标和基于OOB数据置换的MDA指标。基于OOB数据置换的MDA指标可直接度量每个特征变量对模型精确度的影响程度，不存在MDI指标的偏向问题，使用范围广泛[9]。

基于OOB数据置换的MDA指标的主要思路：保证其他特征变量不变，只打乱OOB数据中的某个特征变量的顺序，破坏OOB数据的特征变量与输出之间的对应关系。利用决策树分别对打乱前与打乱后的OOB数据进行预测，将所有决策树前后两次预测的均方误差的平均值作为此特征变量的重要性测度结果[18]。基于OOB数据置换的MDA指标的求解过程如下。

Step1:随机森林包含M棵决策树H={h1,h2,…,hM}。分别利用每棵决策树hm(m=1,…,M)对相应的OOB数据(OOB数据的输入矩阵为xOOB，输出响应向量为Y)的输入矩阵进行预测，预测结果为Ym，则预测值Ym与真实值Y的均方误差εm=mean(Ym-Y)2。

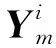
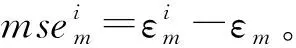
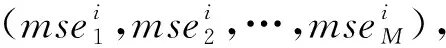
(12)

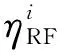
3 基于随机森林的重要性测度与方差全局灵敏度指标的关系

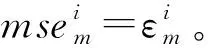
3.1 均方误差与灵敏度总指标的关系

(13)

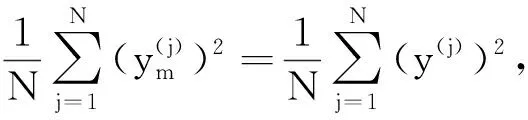
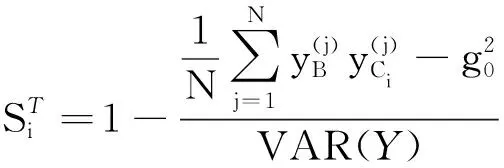
(14)

对比式(13)和式(14)可以得出

(15)

3.2 均方误差与灵敏度主指标Si的关系

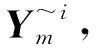
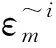
(16)

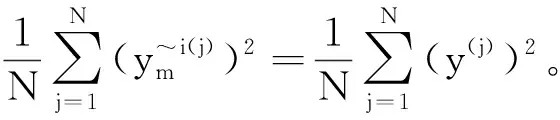
(17)

对比式(16)和式(17)可以得出

(18)

4 基于随机森林的组变量重要性测度

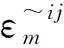
(19)

在单层Monte Carlo模拟法中，矩阵B中的第i、j列被矩阵A中的第i、j列代替后可求得组变量的主指标S[i,j]，S[i,j]与单一变量的主指标Si与Sj以及两变量交互指标Sij的关系为[1]

S[i,j]=Si+Sj+Sij

(20)

(21)

其中，上标“～i”“～j”“～ij”分别表示带外数据中除第i列、第j列以及第i和第j列以外的数据打乱顺序带来的预测精度的影响。

5 算例与分析

算例1:线性函数

Y=X1+X2+X3

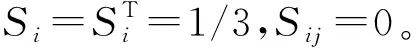
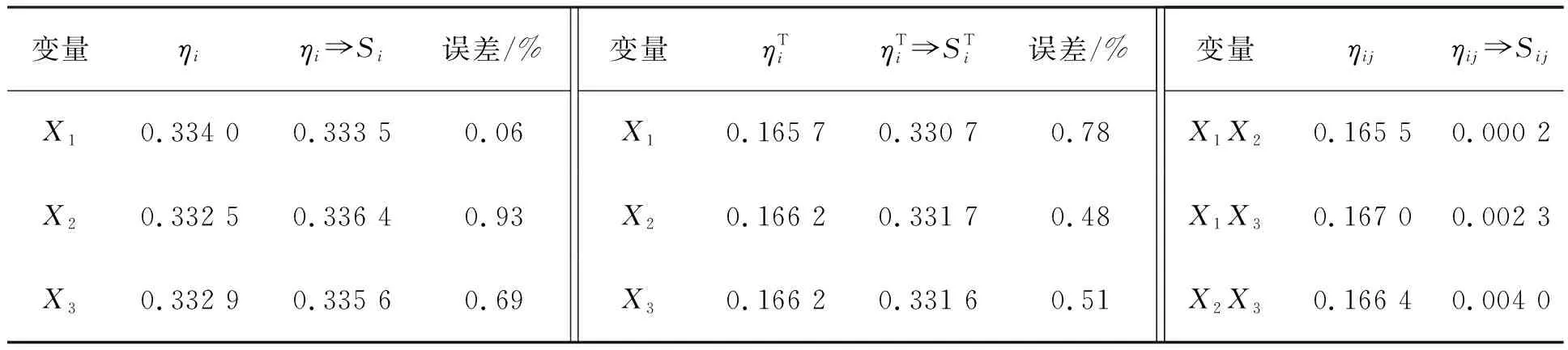
表1 线性函数的变量重要性测度分析结果Tab.1 The variable importance measures for linear function

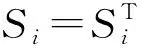
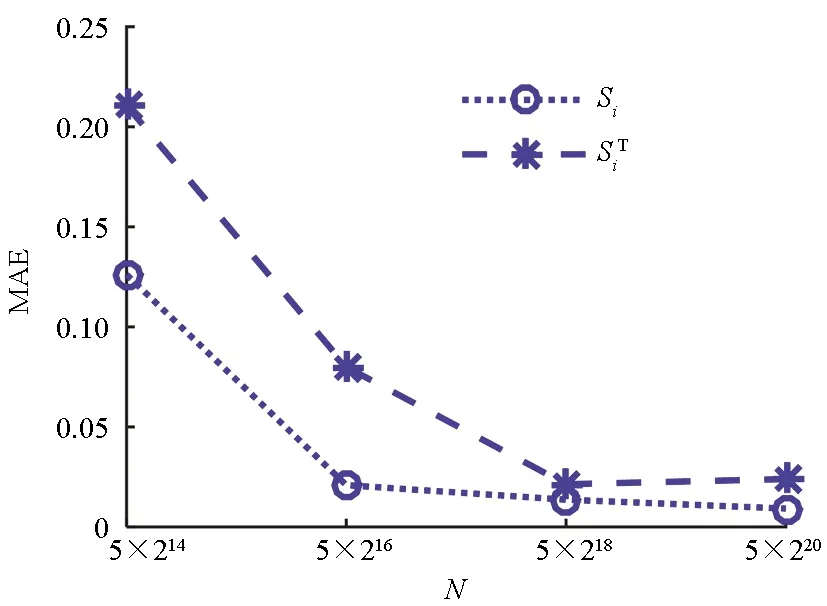
(a) 基于单层QMC模拟的方差灵敏度分析(a) Single-loop QMC simulation for variance-based sensitivity analysis

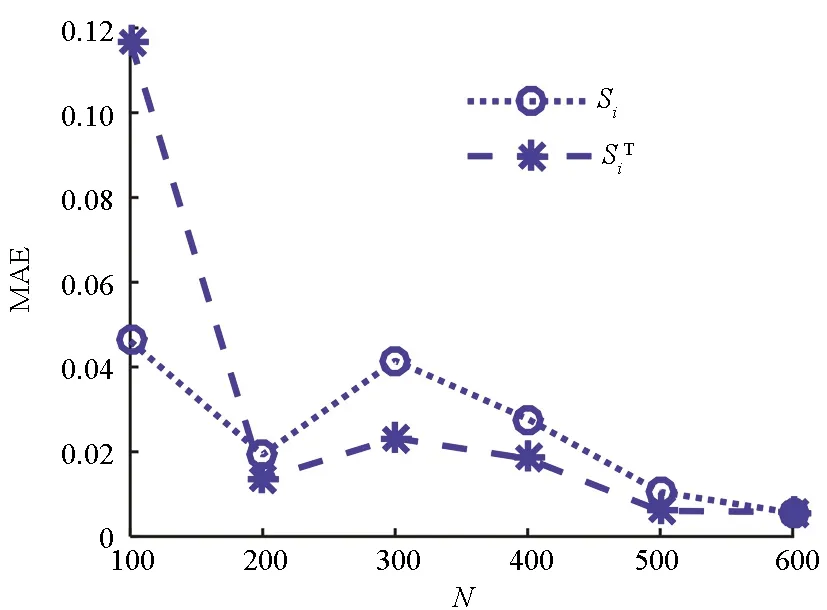
(b) 基于随机森林的重要测度分析(b) Random forest for importance measure analysis图1 线性函数的方差灵敏度误差随样本量的变化曲线Fig.1 Error of variance-based sensitivity indices versus sampling number for linear function

算例2:Ishigami函数[19]

其中，Xi(i=1,2,3)相互独立，均服从[-π,π]区间的均匀分布。函数的方差VAR(Y)≈13.846 0。采用随机森林对Ishigami函数进行重要性测度分析，以变量X2为例，基于单层QMC模拟的方差灵敏度指标、随机森林进行重要性测度推得方差灵敏度的误差随样本量的变化曲线如图2所示。随机森林用300个训练样本、700个OOB样本进行重要性分析，可获得误差小于2%的测度指标，分析结果列于表2。

(a) 基于单层QMC模拟的方差灵敏度分析(a) Single-loop QMC simulation for variance-based sensitivity analysis

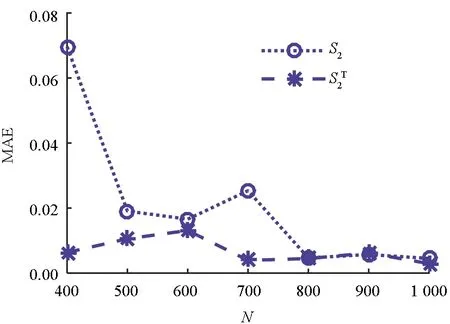
(b) 基于随机森林的重要测度分析(b) Random forest for importance measure analysis图2 Ishigami函数的方差灵敏度误差随样本量的变化曲线Fig.2 Error of variance-based sensitivity indices versus sampling number for Ishigami function

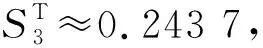
表2 Ishigami函数的变量重要性测度分析结果Tab.2 Variable importance measures for Ishigami function

算例3:系统失效树模型[20]

Y=X1X3X5+X1X3X6+X1X4X5+X1X4X6+

X2X3X4+X2X3X5+X2X4X5+X2X5X6+

X2X4X7+X2X6X7

(22)

式中，X1、X2代表事件每年发生的次数，X3～X7代表了基本事件的失效率，各变量相互独立，均服从对数正态分布，分布参数如表3所示。将大样本(N=9×221)下的单层QMC模拟的结果作为方差灵敏度的近似精确解，函数的方差VAR(Y)≈1.606 8×10-8，与随机森林重要性测度分析结果对比见表4。

表3 失效树模型的变量分布信息Tab.3 Distribution information of input variables in fault tree model

算例3的变量维数n=7，需要较多的样本(3 000个训练样本，5 000个OOB数据)来保证随机森林的精度。由表4的结果可以看出，基于随机森林的重要性测度推得的方差灵敏度与单层QMC模拟的近似精确解基本一致，变量的重要性排序相同，X2、X6、X5为重要变量。此外，对变量的交互作用也进行了重要性分析，得到最大的两个交互灵敏度指标为：S25≈0.021 9，S26≈0.026 3。

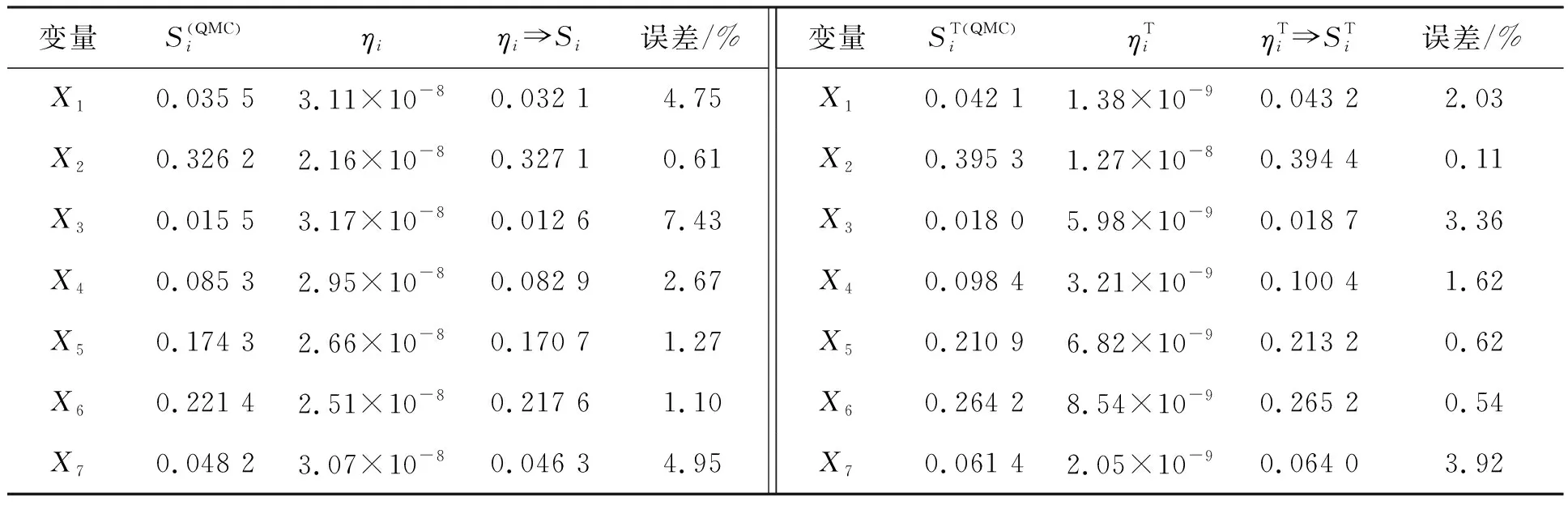
表4 失效树模型的变量重要性测度分析结果对比Tab.4 Variable importance measures for fault tree model

算例4:屋架结构

某屋架结构如图3所示，屋架的上弦杆和压杆采用钢筋混凝土杆，下弦杆和拉杆采用钢杆。设屋架结构承受垂直的均布载荷q的作用，将均布载荷q化成节点载荷P，则P=ql/4，通过力学知识可得C点的垂直位移为

(23)

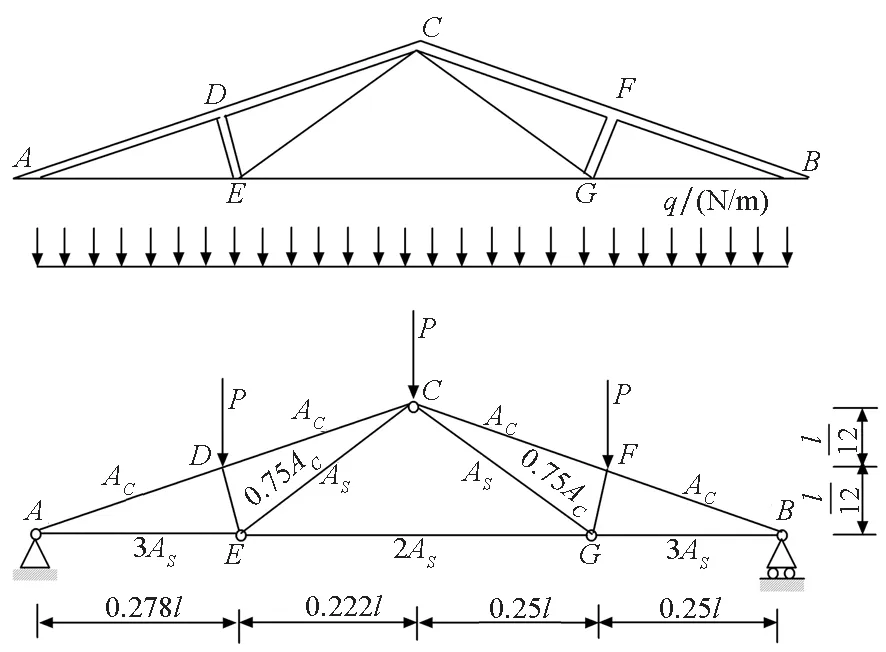
图3 屋架结构的简单示意图Fig.3 Roof truss structure

式中，AC、AS、EC、ES分别为钢筋混凝土杆与钢杆的横截面积与弹性模量，l为杆长，假设所有输入变量相互独立，且服从正态分布，分布参数如表5所示。

表5 屋架结构的变量分布参数Tab.5 Distribution parameters of input variables in roof truss structure

响应函数的方差VAR(ΔC)≈1.626 6×10-6。以大样本(N=8×220)下的单层QMC模拟结果作为近似精确解。随机森林用1 000个训练样本、5 000个OOB数据进行重要性测度分析。

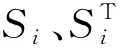
表6 屋架结构的变量重要性测度分析结果对比Tab.6 Variable importance measures for the roof truss structure

6 结论

1)将决策树的叶节点由原始的取平均或线性拟合变为高精度的Kriging模型，使得改进后的决策树对原响应函数有更好的拟合精度。

2)在基于随机森林的MDA指标的分析基础上，提出了单变量和组变量重要性测度指标，完善了基于随机森林的重要性测度指标体系。

3)找到了基于随机森林的重要性测度指标与基于方差的全局灵敏度主指标、总指标之间的关系，可用随机森林的重要性测度指标推导出方差灵敏度指标，获得方差灵敏度指标求解的新途径。

4)本文只研究了独立变量对输出响应的影响，后续将开展基于随机森林的相关特征变量的重要性测度分析方面的研究。