对“入射粒子能量为阈能时的核反应是完全非弹性碰撞”的更一般性证明

苏国珍

(厦门大学 物理科学与技术学院，福建 厦门 361005)

文献[1]给出了“入射粒子能量为阈能时的核反应是完全非弹性碰撞”这一结论的一种证明，但只针对比较特殊的情况，即反应后生成两个粒子.一个粒子入射到一个静止的靶产生核反应后，可能生成一个粒子、两个粒子或更多个粒子.若只生成一个粒子，入射粒子的动能是定值；如果生成两个或两个以上的粒子，则入射粒子的动能不是唯一的.使得核反应能够发生所需要的入射粒子的最小动能称为反应阈能.本文将针对更一般的情况，即反应后生成n(n≥2)个粒子，给出上述结论的证明.

考虑以下核反应：

A+B→C1+C2+…+Cn

(1)

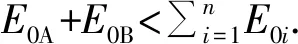
1 通过动量-能量矢量变换证明

在质心参照系中，根据能量守恒，有

(2)

质心参照系中系统的总动量为零，即

(3)

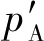
(4)

(5)

式中c为真空中的光速.由式(2)～(5)可解得：

(6)

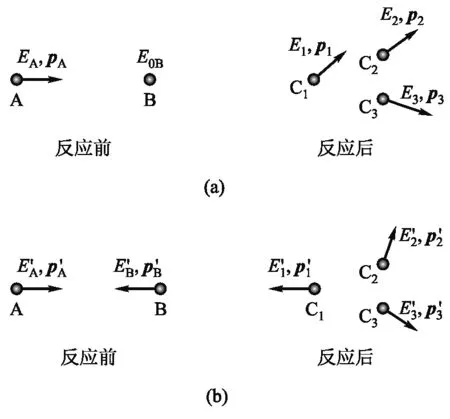
图1 实验室参照系与质心参照系中的核反应

(7)

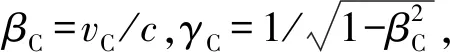
(8)

(9)

由式(8)可得

(10)

(11)

将式(10)和(11)代入式(9)，并利用式(3)和(4)，可得

(12)

最后，将式(6)和(7)代入式(12)，我们得到实验室参照系中粒子A的能量：

(13)

其动能为

(14)

(15)

时，入射粒子的动能最小.此时反应产生的粒子在质心参考系中都处于静止状态，在实验室参照系中以共同的速度vC运动，即核反应是完全非弹性碰撞.将式(15)代入式(14)，得到入射粒子动能最小值，即阈能为

(16)

2 通过动量-能量矢量不变量证明

利用动量-能量矢量不变量[2]，可更方便地证明上述结论.由动量p和能量E构成的四维矢量(p,iE/c)，其内积p2-E2/c2是一个与参照系无关的不变量，这一性质还可以推广到质点系，即(∑p)2-(∑E)2/c2是不变量.将这一结论应用到粒子A、B组成的质点系，可得

(17)

根据式(17)，结合式(2)、(3)以及粒子A的动量与能量所满足的关系

(18)

不难得到粒子A能量的表达式，其结果为式(13).余下的证明过程与上述相同，不再赘述.