麦克斯韦速率分布的特色推导方法

冯仕猛

(上海交通大学 物理与天文学院，上海 200240)

平衡状态下的理想气体分子以不同的速度运动，由于碰撞，每个分子的速度都不断地改变，使分子具有各种速度.因为分子数目很大，分子速度的大小和方向是无规的，所以无法知道具有确定速度u的分子数是多少,但可知道速度在u1与u2之间的分子数是多少.1859年，麦克斯韦首先获得气体分子速度的分布规律：在平衡状态下，忽略气体分子间相互作用,分布在任一速率区间的分子数与总分子数的比率满足一定的分布，这就是麦克斯韦速率分布.

麦克斯韦速率分布函数的推导比较复杂，许多教材仅仅给出分布函数的表达式，很少涉及具体的详细推导过程[1-3].文献报道的一些推导方法[4-6],但初学习者学完仍然难以借助该推导来有效记住其表达式和理解其物理意义，物理教学不应该仅仅介绍一些结论性的公式，而应该把这些公式对应的物理图像和逻辑推理给学生解析清楚.只有这样，学生才能把知识学活并能进一步地把握更深层次的物理规律,为他们将来创新性学习和工作奠定坚实的基础.

本文利用速度空间的概念，通过创新性地排列组合法来推导麦克斯韦速度分布律.由于这种方法独特、简单,物理图象清楚,学生课后的反响比较好，得到绝大多数学生的认可.

1 理论推导

首先,假定体积为V的容器内一定量的理想气体处于平衡态下,气体总分子数为N.分子的速率分别是v1、v2、v3、…、vi,每个速率对应的分子数分别为N1、N2、N3、…、Ni,而且每个分子是可以区分的，则根据排列组合原理，其总的微观状态分布数为

(1)

因为对于有速度大小为vi的气体分子，如果它在某时刻在空间的某一位置可以往任意方向运动，它往每个方向运动的概率都是相同的.这样就能给出以速率vi为半径的速度球(速度空间)，速度球表面上的每一个点都是该气体分子可能出现的一种状态，该表面积与单位厚度构成的球壳体积就是该气体分子在此速率vi与vi+dvi(dvi=1)之间可以选择的状态数多少，如图1所示.

图1 速度球模型

如果分子速率分别是v1、v2、v3、…、vi,对应分子数分别为N1、N2、N3、…、Ni,，单个分子对应的状态数分别是：

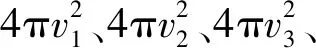
(2)

因此，式(1)对应的微观状态数就进一步修正为

(3)

利用lnN!=NlnN-N，对式(3)两边取对数得

(4)

将式(4)简化为

(5)

然后对式(5)两边求偏导数得到

(6)

令

(7)

式(7)中U是系统的总动能，Ei是速率vi为单个分子的动能，对式(7)两边求偏导数得到

(8)

利用拉郎隔日法，设函数：

W=lnΩ+αG+βh

(9)

式中α、β是常数.对式(9)两边再求偏导数得到

(10)

将式(6)和(8)带入到式(10)中得到

(11)

当式(11)为0时，对应的Ω极大值，也就是平衡态下概率最大的一种分布.利用

(12)

从式(12)可以得到

(13)

令C=e-α，因为α是常量，所以C是常量.由于系统总的分子数不变，所以

(14)

(15)

(16)

因为式(16)中速度空间球壳的厚度为1，所以对于单个气体分子，根据概率分布的定义，其对应的概率分布为

(17)

根据动量和冲量的关系，理想气体平衡状态下温度与方均根速率关系[7]，可以得如下关系式：

(18)

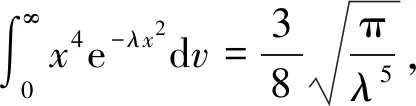
(19)

式(19)就是经典的麦克斯韦速率分布函数，与经典教材上给出的表达式相同，但其推导过程所对应的物理意义比较清楚，而且推导所需要的数学知识并不复杂，低年级大学生基本能完整的理解，这对于他们正确理解麦克斯韦速率分布是非常有用的.

2 讨论

本文的推导相对比较简洁、物理图像比较清楚，但有几点需要特别说明如下：

1) 利用本论文的推导方法给出麦克斯韦速率分布函数，教学中的一个难点是怎么理解速度空间的概念.笔者在教学中，举了一个简单的例子阐述这个概念的物理意义，如一个人站在一个很大的广场中央，他可以选择任意方向运动，如果每秒跑10米，让学生思考有多少个选择的方向.然后让学生想象一下：以起跑点为圆心，速度为半径画一个园，其周长上的任意一点都对应学生可以选择的运动方向，选择的总方向数就等于周长.把一个运动方向当作该学生可以选择的状态，周长就是该学生可以选择的总状态数.由此而导出空间中一理想气体分子以某一速度运动，其选择的状态数就是速度球的表面积；再进一步引申到速度薄球壳的体积就是气体分子在某一个速率处单位速率间隔内可以选择的总状态数，学生就比较容易理解速度球与状态数的关系.

2) 热学教学中，利用理想气体平衡状态下和气体分子与周围容器壁发生弹性相撞的假设条件，再根据经典的力学理论中动量和冲量的关系，首先推导出热力学温度与平均平移动能的关系，就是本文中式(19)中前一等号的部分.按此序教学，学生容易理解相关的概念.

3 总结

本文利用从微观状态数最多的分布出发，引入了速度空间概念，推导出了麦克斯韦速率分布的表达式.这种推导方法直观、简单，便于学生构建相关知识的物理图像以及对该部分内容物理意义的理解，这是本文研究的意义所在.大学物理是大学生最重要的基础课程之一，课程教学过程中，多从不同的侧面或者不同的层面演绎和推导一些重要的知识，对于构建其相关知识点的物理图像、强化学生的空间想象力、培养学生的创新性思维都是非常重要的.