无井地震梯次反演方法研究

李怀懿，王 新，江建虹，蔺 营，郭彦民,张广智

(1.中国石油大学(华东) 地球科学与技术学院，青岛 266580；2.辽河油田勘探开发研究院 新能源所，盘锦 124010)

0 引言

地震反演技术是综合运用地震、测井、地质等资料，以揭示地下目标层(储层、油气层)的空间几何形态(包括目标层厚度、顶底构造形态、延伸方向、延伸范围、尖灭位置等)和目标层微观特征，是目前寻找油气藏最有效的方法之一[1]。目前地震反演方法主要分为叠前反演和叠后反演，但这些反演方法大多是基于已钻井的地质信息、利用测井资料垂向高分辨率和地震资料横向高分辨率特点的综合约束反演技术，它们都能极大地提高反演结果的分辨率。无井工区通常采用叠加速度场建立的速度模型或是道积分反演方法获得的阻抗数据对油气藏进行描述，这些传统的方法一般分辨率较低，不利于对油气藏进行精细描述。

对于无井或少井区叠后地震盲反演[2]发展较为成熟,国内、外很多学者对该方法进行了研究。Wiggins[3]1978年首次提出了第一种盲反褶积的算法，它通过最大化输出序列的峰度即最小化输出序列的熵来达到反褶积的目的；Liu等[4]建立在贝叶斯估计框架的基础上，研究了基于Cauchy 稀疏约束的地震盲反褶积方法；刘财等[5]发展了一种基于自然梯度的地震盲反褶积方法；吴常玉等[6]研究了基于信号负熵理论的地震盲反褶积方法；Li等[7]建立在反射系数统计特征和Bussgang算法的基础上，根据 Kullback-Leibler 距离为度量的目标泛函，实现了地震盲反演。但地震盲反褶积与传统的反演理论不同，由于地震子波和地层反射系数未知，是一个典型的欠定问题，导致问题是多解的，并且很难在盲反褶积过程中对数据进行控制，因此该方法对数据中的各种噪声比较敏感，反褶积的效果很难保证，在很大程度上限制了地震盲反褶积的应用以及进一步的发展。

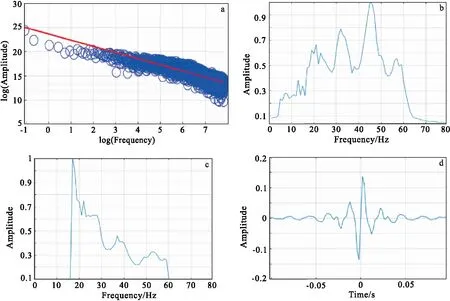
图1 有色反演方法流程Fig.1 Colored inversion workflow(a)测井声波阻抗曲线振幅谱;(b)地震振幅谱分析;(c)反演算子振幅谱;(d)有色反演算子

有色反演方法最早是由BP公司的Lancaster等[8]提出来的一种地震数据带限反演方法，该反演方法简单快捷，不需要地震子波和初始模型的约束，只需设计一个有色反演算子，将地震道直接转换为反演结果，反演结果人为因素少，反映地质现象较为客观[9-10]。

笔者基于离散反演理论，提出以叠加速度场和有色反演结果为初始模型，结合虚拟井法提取的地震子波进行梯次反演，方法简单高效，获得的反演结果较传统反演方法分辨率提高，对无井区勘探初期的储层预测具有一定的借鉴意义。

1 无井反演方法原理

1.1 有色反演

1.1.1 基本原理

有色反演的基本思想是设计一个有色反演算子，将目标工区的地震资料与测井资料中的波阻抗信息直接建立起一种转换关系，最后将有色反演算子直接应用于地震资料中，完成有色反演。

I=O*S

(1)

式中：I为相对波阻抗；O为有色反演算子；S为地震记录；*为褶积运算符。

有色反演的优势是对井的依赖性较小，当工区内无井时，可以利用相邻地质地层情况相似的工区测井资料和地震资料设计有色反演算子，再将有色反演算子应用于无井区地震资料中，完成有色反演。

1.1.2 有色反演流程

首先对工区内测井资料中的波阻抗信息作频谱分析，拟合一条直线来代表理想输出波阻抗IA(f)，并把得到的IA(f)关系式转换到Imp-f域。再对该工区归一化的地震振幅谱进行分析，然后对比两者的振幅谱关系，根据式(2)在频率域内设计有色反演算子，将工区的地震资料与测井资料中的波阻抗信息相联系起来。由于反射系数反应的是界面信息，而波阻抗反应的是地层间信息，道积分反演将反射系数转换为波阻抗，相当于做了90°相移[9]。根据道积分反演的相关观点，这里将有色反演算子做90°相移并转换到时间域，最后将有色反演算子应用于地震资料中，直接将地震资料转换为波阻抗结果，完成有色反演(图1)。

(2)

式中：CIA(f)为有色反演算子振幅谱；IA(f)为理想输出波阻抗；S(f)为地震振幅谱。

由于S(f)是个很小的值，除以它可能会导致CIA(f)趋于无穷大，表现在谱图上会抖动很大，这会导致有色反演算子很不稳定，为了避免算子出现不稳定现象，我们通过设置阈值来处理这个问题，当S(f)低于该阈值时，有色反演算子设置为“1”。为了更好地将地震资料与测井资料中的波阻抗信息相联系起来，有色反演算子的低通频率取值在10 Hz左右，高通频率取值应根据实际地震资料频谱特征适当调节，以高频能量开始下降点为参考，取值不能过大。

1.2 无井地震子波的提取

一般来说，地震子波的提取方法主要分为两大类：①确定性地震子波提取方法;②统计性地震子波提取方法[12-14]。确定性地震子波提取方法是在已知测井资料或者VSP资料的条件下，计算出地层实际的反射系数序列，然后结合井旁地震道由褶积模型求得较为精准的地震子波。统计性地震子波提取方法则不需要测井信息，完全依靠地震数据本身所蕴含的信息，但需要对地震资料和地下反射系数序列的分布进行某种假设,所得到子波精度与假设条件的满足程度有关。

笔者针对无井区的情况，采用张广智等[15-16]提出的虚拟井法提取地震子波。

1.2.1 基本原理

虚拟井法是以层序地层学原理为基础，通过地震层序分析来实现的。根据杜世通教授[17-18]的研究表明，地质体是由地质界面和内部结构组成，地震数据是地下地质体的综合反映，不仅包含界面信息，而且还包含岩性的韵律结构信息，地质体的沉积旋回性结构与地震数据的时频谱相联系，不同的频率段滤波结果可以反映不同级层序体的沉积性质。

方法实现分两步：①对地震道进行时频分析，使用小波变换将地震道分解到不同的频率段;②分别求取不同频率段上的反射系数,并将其小波逆变换合成生成虚拟反射系数，最后结合地震道由褶积模型求得地震子波。

1.2.2 虚拟反射系数及地震子波的求取

杜世通教授[15]提出不同的频率段滤波结果可以反映不同级层序体的沉积性质，并使用时频分析方法进行地震层序分析。小波变换是实现时频分析非常好的工具，而且易于实现信号的合成，因此笔者选用小波变换对地震道进行时频分析。

小波变换分解的N个滤波器相当于是带通滤波器，相互之间有重叠。若我们使用了N个滤波器作时频分析，将地震道分解为N道，相当于把地震数据分解到不同的层序尺度，第K(1≤K≤N)道上的局部极值就与相应的层序体的分界面对应，它的大小反应了反射的强度。由于地震道不一定是零相位的，因此，先对第K道作Hilbert变换(相当于计算信号的包络)，生成复地震道，假设强的反映层序界面的反射系数出现在包络的极值处，因此将瞬时振幅的极值作为分界面的极值。如上所述，依次对N道全部处理完毕后，再用小波逆变换合成每个尺度的反射系数，得到虚拟反射系数。

由得到的虚拟反射系数结合地震道，根据离散反演理论[17]求取地震子波，构建目标函数为式(3)。

(3)

式中：S为地震道；R为反射系数；W为待求的子波；W0为初始的地震子波；CW为地震子波的协方差对角矩阵，相当于初始子波的自相关；CS为地震道的协方差对角矩阵，相当于合成地震记录的自相关。

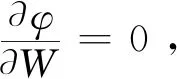
(4)

1.2.3 模型试算

根据上面的方法，对图2(a)所示的地震合成记录进行时频分析并求得虚拟反射系数(图2(b))。再利用虚拟反射系数，根据式(4)求得地震子波(图3)。由图3可以看出，求得的强反射系数的位置是准确的，只是个别的反射系数的幅度有一些差异，从而造成子波的差异，总体说明该方法具有可行性。

虚拟井法提取地震子波的方法要求地震资料的信噪比较高，否则会影响地震子波的准确度。

1.3 波阻抗反演

1.3.1 递推反演方法

递推反演[20]是根据初始波阻抗利用递推关系，计算各层波阻抗值的一种简单的地震反演方法。根据地震波传播理论，地层反射系数可用式(5) 表示。

(5)

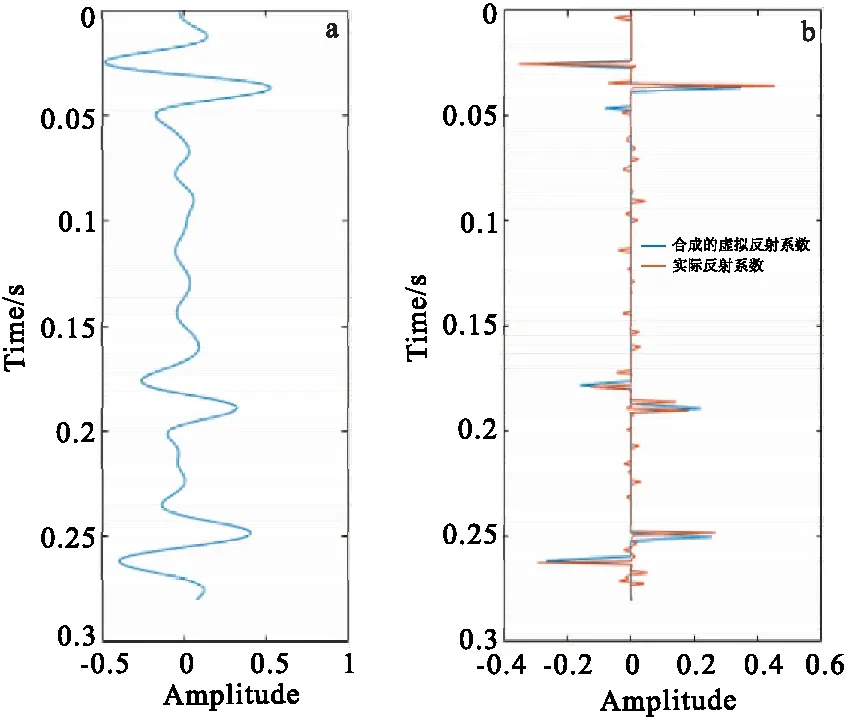
图2 虚拟反射系数的求取Fig.2 Determination of pseudo reflection coefficient(a)地震合成记录;(b)反射系数对比图

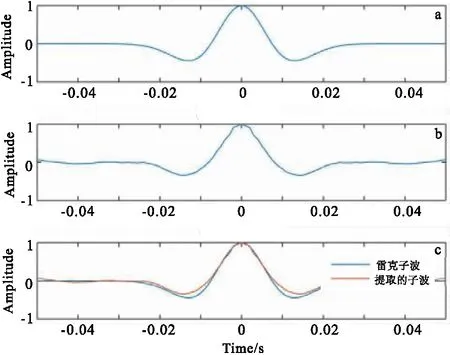
图3 地震子波对比图Fig.3 The comparison of seismic wavelet(a)雷克子波；(b)提取的子波；(c)子波对比图

其中：ρi、ρi+1分别为上、下两层介质的密度；Vi、Vi+1分别为上、下两侧介质中的地震波传播速度；Zi、Zi+1分别为上、下两层介质的波阻抗。

由式(5)可变形得到地层间波阻抗的递推关系式(6)。

(6)

1.3.2 基于模型反演方法

地震记录S(t)是反射系数R(t)和地震子波W(t)的褶积和噪声N(t)构成：

S(t)=R(t)*W(t)+N(t)

(7)

基于模型反演方法[21]建立在褶积理论基础之上，该方法的基本思想是：通过对地层的地震波阻抗模型进行正演模拟，获得一个合成的地震记录，通过与实际地震记录比对计算残差，从而对地震波阻抗模型进行修改，通过反复的比对修改，使得合成记录和实际地震记录近似匹配，从而获得较为精准的地震波阻抗模型。

以绝对波阻抗结果为初始模型，由模型计算合成地震数据与实际观测的测井数据的误差能量为最小，根据最小二乘法有：

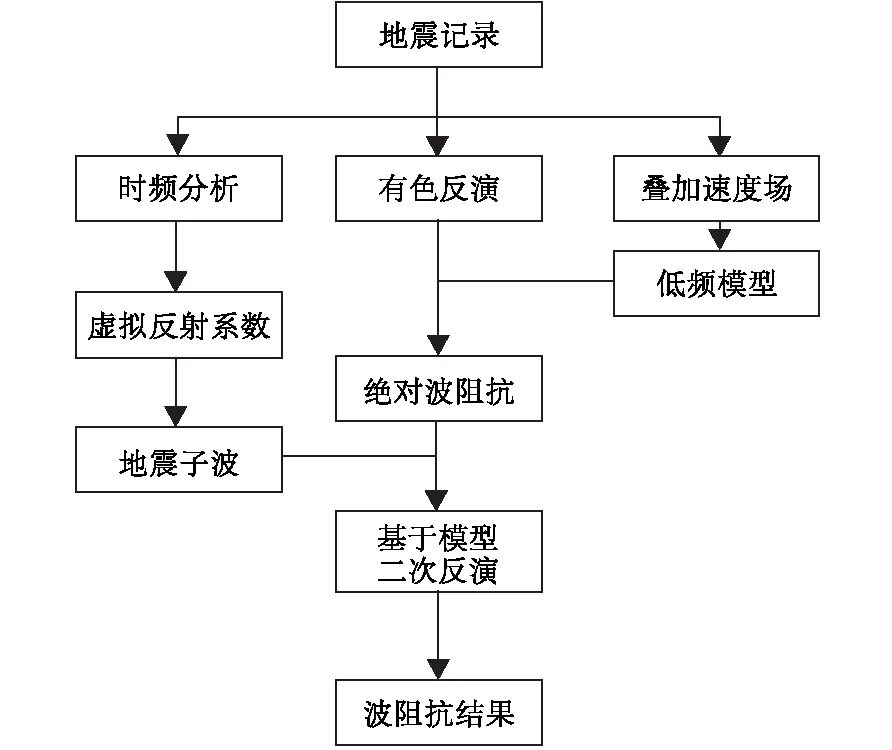
图4 无井地震梯次反演方法流程图Fig.4 Well-free cascade inversion workflow

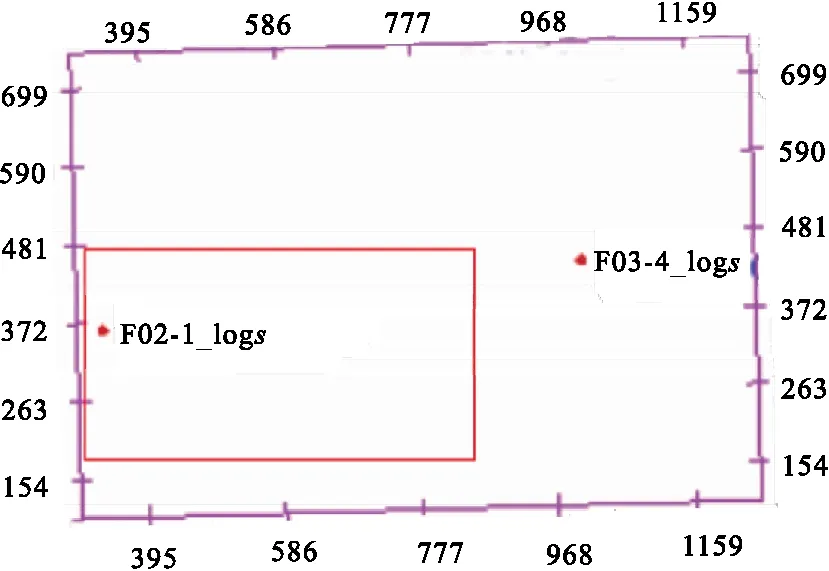
图5 F工区井点分布图Fig.5 The well distribution map

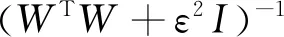
(8)

其中：M为更新后的模型；M0为初始模型；W为提取的地震子波；ε2为阻尼系数；S为实际地震数据；D为模型计算得到的合成地震记录。

2 无井地震梯次反演方法流程

对于无井区域，首先用叠加速度场资料建立低频模型[22]，再利用相邻地质情况相似的工区测井资料及地震资料，设计出一个有色反演算子，将该算子直接应用于无井区地震资料，获得的有色反演结果与低频模型合并得到绝对波阻抗结果。假设无井工区内的地震地质特征和地震数据与相邻工区类似，并在相邻工区得到的是零相位子波，地震数据经过稳定相位法处理后，则可以在无井工区内利于虚拟井法提取一个零相位子波。最后将绝对波阻抗结果作为初始模型，结合虚拟井法提取的地震子波进行梯次反演，以获得更为精细的波阻抗结果。

图6 F地震剖面Fig.6 Seismic profile

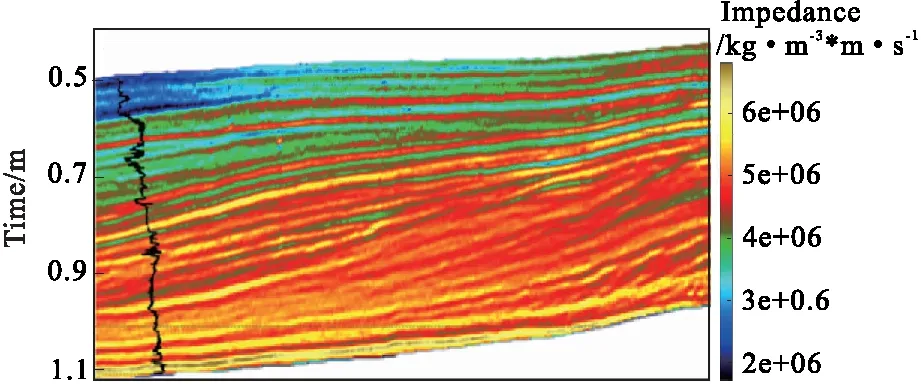
图7 道积分反演的波阻抗结果Fig.7 The result of trace integration technology

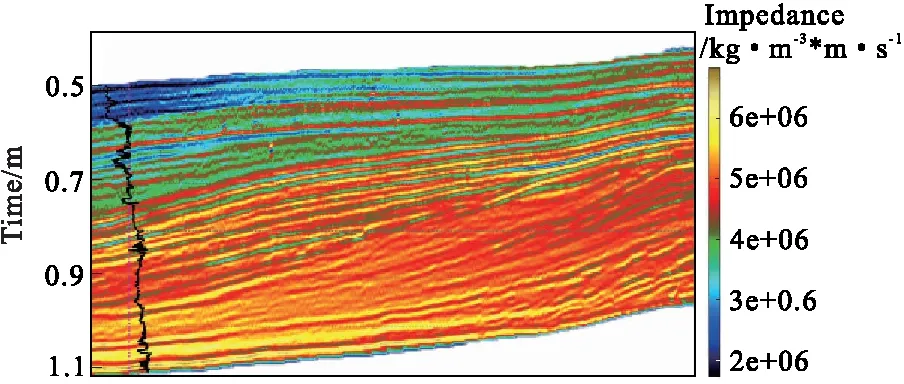
图8 基于模型反演的波阻抗结果Fig.8 The result of model-based inversion

3 实际应用

图5为Opendtect公司的F工区[21]井点分布图，将井F02-1作为盲井进行验证。首先对无井工区的地震剖面(图6)进行传统的道积分反演，反演的波阻抗结果如图7所示。

再采用这里提出的梯次反演方法，首先对相邻地质情况相似的井F03-4所在工区进行分析，将地震资料与井中波阻抗信息建立统计关系，设计出有色反演算子，然后将该算子应用于无井工区，完成有色反演。以叠加速度场和有色反演合并结果作为初始模型，结合虚拟井法提取的地震子波进行基于模型的梯次反演，获得的波阻抗反演结果如图8所示。

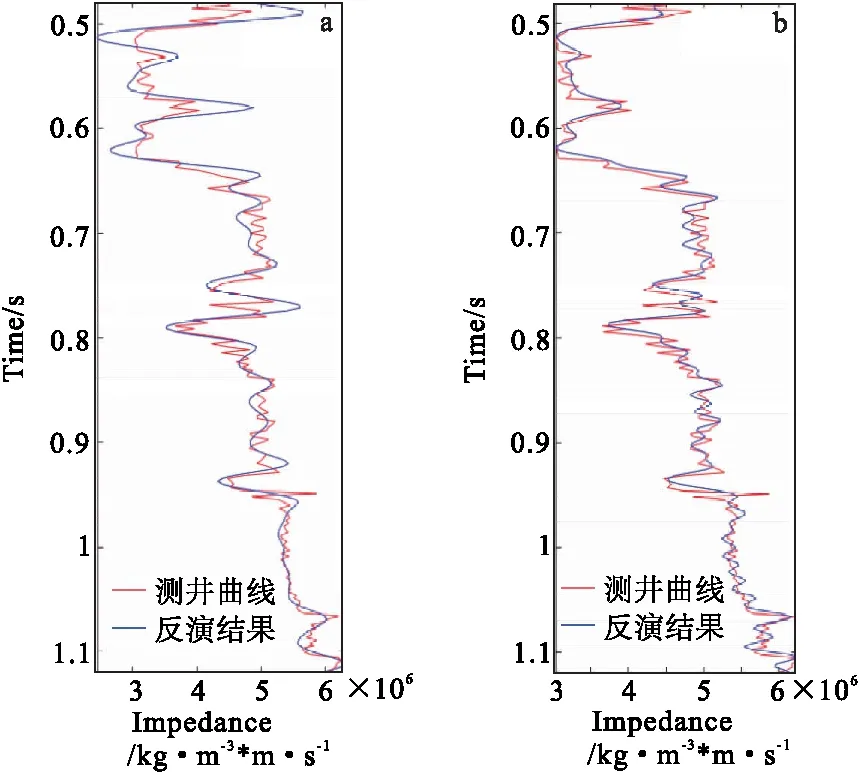
图9 反演结果与F02-1测井资料对比Fig.9 The comparison of inversion result and F02-1 well log(a)道积分反演结果与测井资料对比;(b)梯次反演结果与测井资料对比

图9为验证井所在道的道积分反演结果、梯次反演波阻抗结果与F02-1测井资料的对比图。从图9中可以看出，利用笔者提出的无井地震梯次反演方法获得的波阻抗结果与测井资料大体趋势上相匹配，比无井区常用的道积分反演方法获得的波阻抗信息更为精细，验证了本文提出的反演方法的可行性。

4 结论

1)利用笔者提出的无井地震梯次反演方法，同传统的无井反演方法相比，计算简单高效，获得的反演结果分辨率有所提高，能够较好地解决无井区的反演问题。

2)有色反演算子的准确性对反演结果影响较大，有色反演算子的频带范围应该根据实际地震资料频谱特征调节，当无井工区与相邻工区的地质地层情况越相似，由相邻工区计算得到的有色反演算子应用于无井工区的效果就越好。

3)虚拟井法求出的虚拟反射系数比较稀疏，是由于地震是带限的，它的频带窄于反射系数的频带，因此该方法主要适用于地层较为简单，分辨率和信噪比高的地震资料。

4)通常实际的地震子波相位不为零，可以采用高阶统计量的方法估算出子波相位，以获得更准确的地震子波。

致谢

感谢编辑部和审稿专家对本文修改提出的建议，感谢CGG公司提供软件用于数据成图。