航空大地电磁响应特征分析及反演研究

李 赓，曹飞翔，李万开

(河南理工大学 物理与电子信息学院，焦作 454150)

0 引言

大地电磁测深法是一种天然源频率域电磁法，其以自然产生的平面电磁波为场源，通过观测地表正交的电磁场分量获取地下的电阻率结构[1]。然而，在地形较为复杂的地区，地面大地电磁法施工效率较低，大面积勘探成本急剧上升。目前，航空大地电磁法具有机动灵活、成本低、效率高的优点，能够在复杂环境中进行大规模快速勘探，在国外已被应用于油气勘探、矿产资源勘探等领域[2-3]。

航空大地电磁法通过搭载在直升机上的探测设备采集垂直磁场信号，同时在地面基站采集水平磁场信号，获得倾子数据。经反演[4-5]计算，得到地下介质的电性结构。虽然倾子数据对电阻率的横向变化敏感，可以展示横向电阻率变化引起的异常响应，但缺乏背景电阻率的信息。结合地面大地电磁数据和倾子数据的反演[6]，可克服只拟合倾子数据的缺陷。

近年来，随着计算机硬件计算能力的提高，有限差分法和有限元法等数值模拟方法逐步得到应用。Sasaki[7]采用有限差分法实现了针对ZTEM倾子响应的正演模拟。有限差分法[8-10]在模拟起伏地形或复杂异常体所构成的不规则界面时较困难[11]，而采用有限元方法[12-14]进行起伏地形或不规则界面模拟时更加容易。

这里实现了二维航空大地电磁有限元正演，分析了起伏地形对航空大地电磁倾子数据的影响。为了解决上述倾子数据缺乏背景电阻率信息的问题，实现了空中倾子数据与地面大地电磁数据的反演算法。通过在倾子数据的反演目标函数中加入地面大地电磁数据约束项，构建了新的反演目标函数，同时引入加权因子对地面大地电磁数据“约束”项进行加权。利用非线性共轭梯度(NLCG)反演算法，开展了带地形的低阻异常体地电模型的倾子反演和倾子与地面大地电磁数据反演研究。

1 二维航空大地电磁正演理论

1.1 边值问题

在航空大地电磁法中，空气中电阻率一般设置为108，位移电流的大小跟电导率和频率成正比。因此，可忽略位移电流对场分布的影响。取时谐因子为e-iωt，于是谐变场的麦克斯韦方程组可表示为：

(1)

由麦克斯韦方程组可进一步推导出

TE极化模式：

(2)

TM极化模式：

(3)

从TE和TM模式极化公式中可以看出，磁场分量只存在于TE模式之中，TE极化模式下二维航空电磁法的控制方程表示为：

(4)

公式(4)可进一步表示成：

(5)

式中：u=Ex;τ=1/iμω;λ=σ。

为了求解式(5)，还须给出边界条件。现假设求解区域如图1所示，笔者所研究对象为天然电磁场，场源在距离地面足够远的高空中，电磁场以平面波的形式垂直入射地下介质。

图1 TE模式求解区域Fig.1 Solution domain for TE polarization

TE模式下的边界条件如下：

1)上边界AB离地面足够远，使异常场在AB上为零，该处的u为“1”。

3)左右边界AD、BC离局部不均匀体足够远，边界条件为∂u/∂n。

综上所述，边值问题可总结为式(6)。

u=1 ∈AB

(6)

1.2 有限元分析

与上述边值问题等价的变分问题为式(7)。

δF(u)=0

(7)

式中：Ω为待求解区域面积;Γ为Ω的边界。

有限单元法在求解上述变分问题时，首先将待求解区域离散为一系列互不重合的四边形单元。接着选用等参单元并构建双二次插值函数进行单元积分。图2展示了母单元(等参单元)和子单元以及其各节点编号，计算时需要将子单元节点坐标映射到定义域为[-1,1]2的等参单元上，并用(ξ,η)表示等参变量。设子单元中心点坐标为(x0,y0)，单元高为b，宽为a，则母单元与子单元之间的坐标映射满足如下关系：

图2 四边形单元Fig.2 Quadrilateral unit(a)母单元;(b)子单元

(8)

坐标之间微分关系为式(9)。

(9)

则四边形母单元的双二次插值函数形式如下：

(10)

然后在各离散单元内用插值函数与单元中节点上未知电场值的乘积作为近似解，将近似解带入边值问题后，在每个单元上可得一个复系数线性方程组。向该复系数线性方程组中加入求解边界条件(定解条件)，假设为u=b。最终可得到一个大型稀疏对称复系数线性方程组，该大型稀疏对称复稀疏线性组表示为式(11)。

(11)

式中:Ke和ue分别为单元系数矩阵和向量；Ne为单元总个数，采用直接求解法求解该方程组即可得到求解区域内各节点电场值组成的向量。

1.3 倾子响应计算公式

航空电磁法中倾子响应的表示为式(12)。

Hz(r)=Tzx(r,r0)Hx(r0)+

Tzy(r,r0)Hy(r0)

(12)

式中：r为空中垂直磁场分量数据采集点位置；r0为地面水平磁场分量数据采集点位置；Tzx、Tzy分别为倾子数据的两个分量。

由于磁场分量Hz只存在于TE模式之中，因此，二维航空电磁法中倾子数据只存在Tzy分量，其计算公式为式(13)。

(13)

2 反演理论

2.1 反演目标函数的建立

为实现倾子数据与地面大地电磁数据的反演，我们在构建目标函数时加入对地面大地电磁数据的约束项，如式(14)所示。

(14)

最终该反演目标函数的完整形式如下：

λmTLTLm

e=d-F(m)

eMT=dMT-FMT(m)

(15)

2.2 反演目标函数梯度的求取

基于Rodi W[15]的文献，采用非线性共轭梯度(Nonlinear conjugate gradients,NLCG)算法求解新反演目标函数的极小值。这里的新目标函数中，加入了对地面大地电磁数据的约束项，此处与经典目标函数不同，如式(15)所示。另外，视电阻率与倾子的计算公式不同，因此在求解正演算子的雅可比矩阵的过程有所不同。

倾子数据及正演算子可表示为：

(16)

式中：向量a、b可实现电场值向磁场值的映射；u表示电场分量Ex；雅可比矩阵A是正演算子的偏导数，即∂F(m)/∂m，可表示为：

(17)

其中：i=1,2,…,N；j==1,2,…,M。

视电阻率以及正演算子FMT(·)可表示为：

ρa=-Ex/(1/iωμ)(∂Ex)/∂z)

FMT(m)=lnρa=

(18)

式中：i表示虚数单位；向量h、k可实现电场值向电场值、磁场值的映射。而该正演算子的偏导数为雅可比矩阵C,可表示为式(19)。

(19)

其中:i=1,2…,NMT;j=1,2…,M。

3 算例

3.1 数值模拟算例

3.1.1 正确性验证

为了验证本文有限元算法的正确性，设计了如3所示的二维低阻块体模型。该模型的背景电阻率为100 Ω·m，异常体的电阻率为10 Ω·m，其顶层距离地表1 000 m，横向宽度为2 000 m，垂向高度为 2 000 m。空中测线位于地表以上100 m处(图3中红色虚线)，频率选择为0.01 Hz、1 Hz和100 Hz，分别计算了倾子实部和虚部，并将计算结果与MARE2DEM程序[16]计算结果进行了对比如图4、图5所示。

图3 低阻块体模型Fig.3 Low resistivity block model

图4 倾子实部对比曲线图Fig.4 The real part of tipper comparison curve

图5 倾子虚部对比曲线图Fig.5 The imaginary part of tipper comparison curve

图6 倾子实部相对误差曲线图Fig.6 The real part of tipper relative error curve

图7 倾子虚部相对误差曲线图Fig.7 The imaginary part of tipper relative error curve

图8 起伏地形模型示意图Fig.8 The schematic diagram of undulating terrain model

图9 倾子响应实部Fig.9 The real part of tipper

图6、图7分别展示了各不同频率倾子实虚部相对误差曲线，从图6、图7中可以看出各分量相对误差均小于0.7%，说明本文数值模拟算法的正确性。

3.1.2 起伏地形

图10 倾子响应虚部Fig.10 The imaginary part of tipper

图11 异常体反演模型Fig.11 Anomaly model for inversion

为了分析倾子数据在起伏地形环境下的响应特征，将图8所示的起伏地形正演模型(背景电阻率值为500 Ω·m的均匀半空间)中的山谷和山脊地形，设计为地形范围位于-3 000 m≤y≤-1 000 m和1 000 m≤y≤3 000 m内，最大地形为500 m。空中测线位于地形以上100 m，如图8中红色虚线所示。在-4 000 m≤y≤4 000 m范围内每间隔50 m采集磁场垂直分量，在地表y=-5 000 m处采集磁场水平分量。选择30 Hz、103.923 Hz和360 Hz频率计算倾子响应值。图9和图10分别展示了起伏地形各频率倾子响应值的实虚部。

通过分析起伏地形倾子响应可知，起伏地形的存在使倾子实虚部响应值曲线偏离于零值(平地形倾子响应为零)，这种地形效应主要出现在山谷和山脊地形处，且随着频率的增加，倾子响应曲线的偏离程度逐渐增大。这是由于高频段信号携带的浅部介质的电性结构信息较多，当地表处电性结构发生变化时，高频段信号也会随之发生明显变化，而低频段信号反映的是深部介质的电性结构，地表处的电性结构变化对其影响较小。

3.2 反演算例

我们对图11中带异常体的起伏地形模型进行反演。模型的背景电阻率为500 Ω·m,在山脊和山谷下方分别嵌入一个电阻率为10 Ω·m的异常体，其高度为500 m，宽度均为800 m，山谷地形下的异常体顶面距离其地形最低处750 m，山脊地形下的异常体顶面距离其地形最高处1 250 m。图11中，航空测线位于地形以上100 m。

图12 500 Ω·m均匀半空间初始模型航空大地电磁反演结果Fig.12 Inversion result of Airborne Magnetotelluric with 500 Ω·m uniform half-space

图13 2 000 Ω·m均匀半空间初始模型航空大地电磁反演结果Fig.13 Inversion result of Airborne Magnetotelluric with 2 000 Ω·m uniform half-space

在-4 000 m≤y≤4 000 m范围内按照20 m间隔共选取401个航空测点，采集空中磁场垂直分量。在地表y=-5 000 m处观测磁场水平分量。在30 Hz～360 Hz频率范围内对数等间隔选择11个计算频率，共生成401×11×2(倾子实部和虚部)=8 822个倾子数据。同时为了进行地面大地电磁数据的联合反演，在-4 000 m≤y≤4 000 m范围内，共放置了12个地面大地电磁数据采集站。在1 Hz～1 000 Hz频率范围内对数等间隔选择13个计算频率值，共生成12×13×2(视电阻率和阻抗相位)=312个地面大地电磁数据。分别向数值模拟计算得到的倾子数据和地面大地电磁数据中加入3%的随机噪声充当实际观测数据。

3.2.1 带地形的倾子反演

均匀半空间模型的倾子为零，倾子的梯度不为零。在进行带地形的倾子反演时，分别将初始模型设置为电阻率值为500 Ω·m和2 000 Ω·m的均匀半空间，其对应的倾子数据反演结果分别如图12和图13所示，由图12可知，当反演初始模型电阻率值与真实背景电阻率值相同时，由于地形的影响，倾子数据反演结果中异常体的位置相对于真实位置整体偏上，异常体的电阻率值也比真实值偏大。

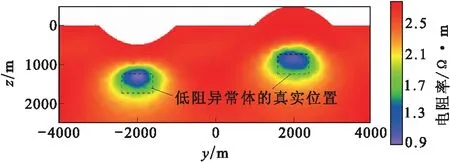
图14 500 Ω·m均匀半空间初始模型联合反演反演结果Fig.14 Inversion result of Joint inversion with 500 Ω·m uniform half-space

图15 2 000 Ω·m均匀半空间初始模型联合反演反演结果Fig.15 Inversion result of Joint inversion with 2 000 Ω·m uniform half-space

由图13可知，当反演初始模型电阻率值与真实背景电阻率值不同时，倾子数据的反演结果与真实电阻率模型相差较大，反演结果中异常体位置、大小未得到有效反映。这是由于倾子数据虽然可以有效表示电阻率的相对变化，但是对电阻率的绝对值约束力不足，当初始模型与真实模型相差较大时，单独的倾子数据反演无法得到一个可靠的反演结果。

3.2.2 倾子与地面大地电磁数据反演

为验证本文反演算法的必要性，我们针对一组加入了相同噪声的倾子和地面大地电磁合成数据，采用不同的反演初始模型分别进行联合反演。在进行倾子与地面大地电磁数据反演时，分别将反演初始模型选择为电阻率为500 Ω·m和2 000 Ω·m的均匀半空间，其反演结果分别如图14和图15所示。

当反演初始模型电阻率值和真实背景电阻率相同时，向倾子数据中加入少量地面大地电磁数据进行反演后，异常体的横向边界可以被清晰的反映出来，同时异常体的反演电阻率值得到了改善，反演效果得到了一定程度的提高。

图13是初始反演背景电阻率值为2 000 Ω·m的倾子反演结果，分析图13和图15可知，加入少量的地面大地电磁数据进行反演，反演结果得到了明显改善。不但两个低阻异常体的边界得到了有效刻画，而且其反演电阻率值也与异常体真实电阻率值较接近。同时对比图14与图15可以发现，当初始模型电阻率与真实模型背景电阻率值差异较大时，少量地面大地电磁数据与倾子数据的反演结果并没有发生巨大改变，这说明通过加入少量的地面大地电磁数据进行反演，可有效地降低倾子数据反演结果对初始模型的依赖。

4 结论

首先采用四边形网格模拟起伏地形，使用有限元方法对起伏地形均匀半空间模型进行数值模拟，分析和总结了起伏地形对航空大地电磁倾子数据的影响。接着对起伏地形异常体模型进行了倾子反演和倾子与少量地面大地电磁数据反演。最终结论如下：

1)起伏地形的存在使得倾子实虚部响应值曲线不同程度的偏离于零值，且随着计算频率的增加，倾子响应曲线的偏离程度逐渐增大。这种地形效应严重影响了航空大地电磁倾子响应曲线的形态，起伏地形不可忽视，会直接影响到航空大地电磁数据资料的处理解释结果。

2)利用倾子数据进行反演时，由于倾子数据对电阻率的绝对值约束力不足，反演结果受初始模型影响严重，当初始模型与真实模型相差很大时，单独的倾子数据反演无法得到可靠的反演结果；通过加入少量的地面大地电磁数据进行反演，可增加观测完备性，从而降低多解性，最终可有效降低倾子数据反演结果对初始模型的依赖。