近垂直定向分布裂缝的各向异性梯度地震反演方法研究

李春鹏,王 哲,李爱山,袁 峰

(1.中海石油 国际能源服务(北京)有限公司，北京 100028；2.中国石油大学(华东)，青岛 266580；3.中海油能源发展股份有限公司 工程技术分公司，天津 300452)

0 前言

裂缝作为地壳中一种普遍的构造现象，广泛存在于各类岩石中。到目前为止，已在砂岩、泥页岩和碳酸盐岩，甚至火成岩等各类岩石的裂缝性储层中获得了大量的工业油气流。实际地层中裂缝呈一种至多种形态，包括近水平定向分布裂缝(VTI介质)、近垂直定向分布裂缝(HTI介质)、倾斜定向分布裂缝(TTI介质)和正交裂缝(OA介质)等。对于近垂直定向分布裂缝(HTI介质)，可以利用各向异性梯度进行预测，各向异性梯度越大，裂缝密度也越大[1-3]。

各向异性梯度可以通过方位地震数据反演得到[4]，宽方位比窄方位包含了更多的各向异性信息，实际生产中一般都利用宽方位地震数据反演各向异性参数[5-6]。不同于三维的叠后数据和四维的叠前数据，方位地震数据是五维数据，目前主要依据炮检距向量片(OVT)技术处理宽方位地震数据，OVT技术是一种新颖的叠前数据的编排方式，基于OVT数据域处理可有效改善宽方位数据处理效果，且OVT域偏移结果含有丰富的方位各向异性信息，能实现宽方位数据的保真处理并提高叠前地震道集的质量，是宽方位三维地震数据的有效处理技术[7]。

地震反演的本质是求解线性方程组[8-9]，线性方程组能否得到良态的解，取决于它的系数矩阵的条件数。条件数越小，线性方程组的解越趋于良态；反之，越趋于病态。对于无约束地震反演方程，其系数矩阵是子波矩阵，然而子波矩阵的条件数特别大，所得到的反演结果是病态的。

为了解决这一问题，一般会对反演方程做加法，即加入高斯分布、柯西分布等数学约束，同时也会加入测井低频约束[10-13]。事实证明，地震反演方程系数矩阵的条件数在加入数学约束和测井低频约束之后显著降低了，反演结果由病态变为良态。

实际工区一般都有测井纵、横波数据，然而各向异性数据却不常有。没有各向异性数据也就没有各向异性低频约束，这样就难以对各向异性反演方程做加法。各向异性梯度反演方程会因缺少测井各向异性低频约束而难以降低反演方程条件数，从而难以得到准确的反演结果[9]。

各向异性梯度反演方程因缺少各向异性测井信息难以做加法，应对各向异性梯度反演方程进行其他改造。笔者基于这种思路，提出了对各向异性梯度反演方程做减法的方法，即稳定的各向异性梯度无井约束反演方法。该方法通过在反演方程中消除子波矩阵和降低反演方程的维数两个减法操作，来降低反演方程系数矩阵的条件数，从而得到稳定的反演结果。

1 常规各向异性梯度反演方法

1.1 各向异性梯度的数学表征

高角度定向排列裂缝地层可以等效为HTI介质，Ruger[4]推导了上、下HTI介质对称轴一致的方位纵波反射系数近似公式，Downton[14]在Ruger基础上将该近似公式进行了线性化，即

(1)

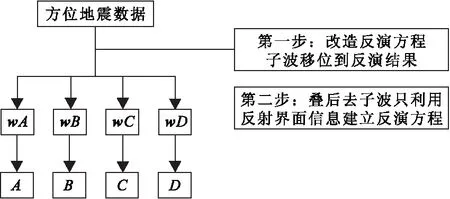
图1 地震反演流程图Fig.1 Work flow of seismic inversion

(2)

通过式(1)可以建立反演方程，据此可以反演得到C和D，然后根据式(2)可以计算各向异性梯度。

1.2 常规各向异性梯度反演方程

方位地震数据的最小二乘反演方程为式(3)。

(WG)T(WG)m=(WG)TS

(3)

式中：S为方位地震数据;W表为子波矩阵;m=[ABCD]T为待反演参数;G为反射系数正演算子矩阵;R为反射系数。

(WG)T(WG)是反演方程的系数矩阵，该矩阵条件数极大，反演结果不稳定。一般都是对该系数矩阵做加法，通过加入高斯分布、柯西分布等数学约束和测井低频约束来降低系数矩阵的条件数，以得到稳定的反演结果。但是实际工区有时会缺少各向异性梯度先验分布信息和测井约束信息，因此难以通过常规反演方程得到真实的地下地层各向异性梯度。

2 各向异性梯度无约束反演方法

常规反演方程做加法的约束项的数学作用在于减小反演方程系数矩阵的条件数，以得到良态的反演结果。其实除了增加约束项，还有消除子波影响和降低反演方程维度的方法来降低反演方程系数矩阵的条件数，该方法分为两步(图1)。

1)改造反演方程，方法是子波移位到反演结果中。假设方位地震数据是方位反射系数，则方位地震数据正演方程如式(5)所示，式(3)和式(5)的最小二乘反演方程如式(6)和式(7)所示。

S=Gm'

(5)

m=[(WG)TWG]-1(WG)TS

(6)

m'=[GTG]-1GTS

(7)

2)叠后去子波，通过地震反褶积将第一步得到的wC和wD数据体转换为C和D数据体，然后通过式(1)～式(5)可以计算各向异性梯度大小和各向异性梯度方向。但是常规反褶积方法是针对每一个采样点计算的，计算量较大且不稳定。一般采用正则化算法改善反褶积算子，但是这种常规反褶积方法得到的反射系数不是稀疏的，不能真正地反映下地层界面的真实情况。笔者依据最少反射层地震反演方法[15]，先搜索目的层地下界面位置，只在搜索的界面位置处建立反褶积方程，这样可以降低各向异性梯度地震记录反褶积方程维数，进一步也会降低反褶积方程条件数，得到稳定的反演结果。

最少反射层稀疏脉冲反演的关键性技术是:首先利用模拟退火法寻找反射层位置，然后利用线性优化方法解目标函数，最终得到准确的反演结果[1,6]。

无约束各向异性梯度反演方法的关键是第一步子波移位，该步骤已经能得到待反演参数，即使反演参数含有子波项，也能体现地下地层的真实情况。另外该步骤简单易操作，只需要把反演方程进行相应改造，即能得到稳定的反演结果。第二步是对第一步的补充，其关键是要能找到地下地层界面的位置，它受限于地震分辨率，一般适用于较厚的地层。实际操作中定义界面数目是同相轴的两倍，能得到较好的结果。

综上所述，无约束各向异性梯度反演方法和常规反演方法,对反演方程的改造存在较大的不同。无约束反演方法对反演方程做“减法”，减去子波项和非界面采样点数，以降低反演方程条件数。而常规反演方法是对反演方程做“加法”，加入统计约束和测井低频约束。虽然二者手段不同，但是目的都是增强反演方程的稳定性，以获得准确的反演结果。但是这并不代表无约束反演方法可以代替常规反演方法，无约束反演得到的是相对结果，常规反演得到的是绝对结果且有更多的约束更符合地质规律。无约束反演更适用于缺少测井资料而难以提供低频约束的情况，是地震反演的权宜之计，若资料允许，还是建议优先使用常规反演方法。

3 模型试算

为了验证以上HTI介质各向异性梯度反演方法的有效性，引用四层三维模型[1-2,9](图2(a))，其中第三层介质是近垂直定向分布的裂缝介质，第一层、第二层和第四层是各向同性介质。第三层裂缝介质的背景弹性参数和物性参数取自于A井的测井信息(图3)，据此可以得到裂缝密度平面分布、裂缝走向平面分布和裂缝走向玫瑰图(图4)。根据以上模型数据可以建立HTI介质弹性矩阵，再根据HTI介质弹性波反射透射方程[16]计算方位反射系数[16]，模型正演采用相移30°后的50 Hz雷克子波，入射角分别是15°、25°和35°，方位角分别是0°、30°、60°、90°、120°、150°和180°。图2(b)显示了inline75，xline50处，入射角是35°，信噪比是10的方位纵波地震记录，图2(b)中最上面的同相轴表示模型第一层和第二层的各向同性界面的方位地震记录，该地震记录不随方位角变化而变化；图2(b)中最下面的两个同相轴分别表示第三层高角度裂缝介质的顶和底的方位地震记录，该地震记录随方位角变化而变化。

各向异性梯度“减法”反演可以分成两步。

1)假设方位地震数据是方位反射系数，使得反演方程隐去子波项，则式(7)反演矩阵GTG条件数约为172。但若采用式(6)的反演方程，则反演矩阵(WG)T(WG)的条件数约为7.3×1017，远大于式(7)计算的反演矩阵条件数，可见式(7)的反演方程稳定性更高。单道反演结果见图5(a)，图5中反演的自激自收反射地震记录wA和各向异性梯度地震记录wB、wC、wD与真实值吻合的较好，说明反演结果比较可信。另外，wC和wD平方根可以表示各向异性梯度地震记录wBani大小，不难发现wC和wD平方根在各向同性界面处几乎为零，在裂缝介质顶、底界面处有值，说明wBani能够指示地层裂缝发育情况。

2)通过地震反褶积将第一步得到的wC和wD数据体转换为C和D数据体，但是以上模型的反褶积算子wTw的条件数约为1.6×1018，反褶积方程极不稳定。因此笔者采用最少反射层假设反演C和D数据体，单道反演结果见图5(b)，其中C和D的平方根可以表示各向异性梯度Bani大小，不难发现C和D的平方根在裂缝地层顶、底界面处有值，其余地层分界面处几乎为零，说明最少反射层假设反演方法能准确体现裂缝地层的发育情况。

将稳定各向异性梯度反演方法推广到整个四层介质模型中，比较图6(a)和图4(a)可以发现，反演的各向异性梯度大小和裂缝密度比较吻合，说明反演的各向异性梯度基本可以反映裂缝地层裂缝密度的平面展布；比较图6(b)和图4(b)可以发现,反演的各向异性梯度方向与裂缝地层裂缝走向基本一致或垂直，另外图6(c)中各向异性梯度方向玫瑰图中有两个互相垂直的主方向，其中18°左右的主方向与图4(c)中的裂缝走向主方向一致，因此各向异性梯度方向可以指示裂缝走向，但是存在90°不确定性，实际裂缝地层预测应用中,需要加入裂缝走向先验信息以辅助识别地层真实裂缝走向。

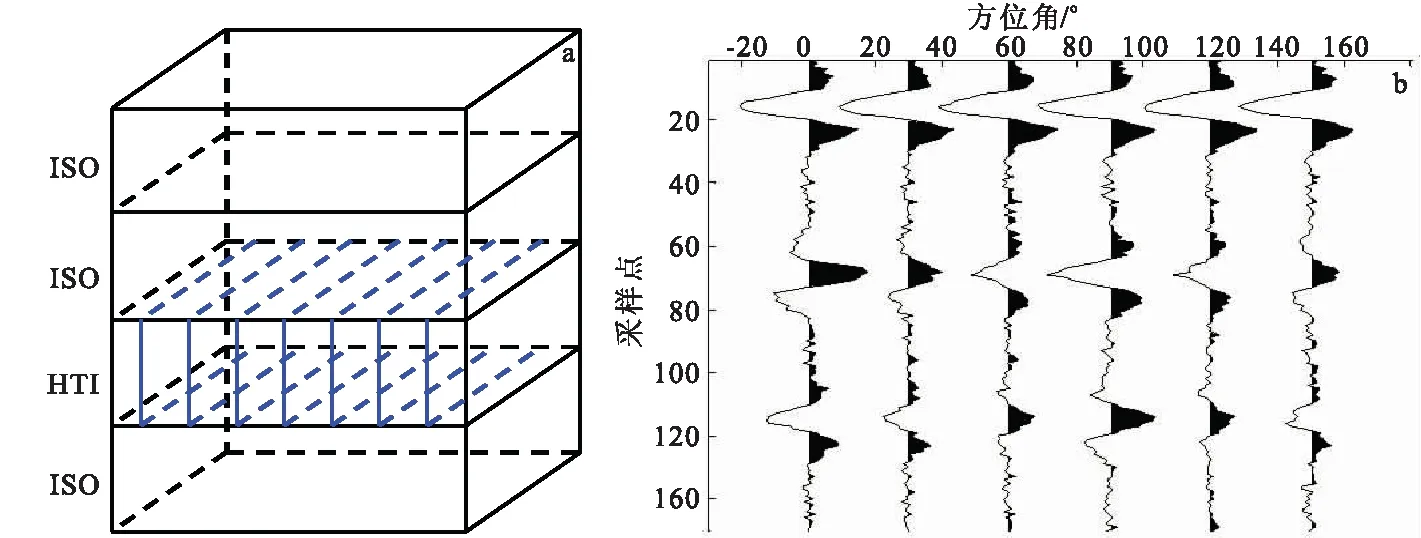
图2 四层介质模型Fig.2 Four layers model (a)示意图；(b)信噪比10的方位地震记录

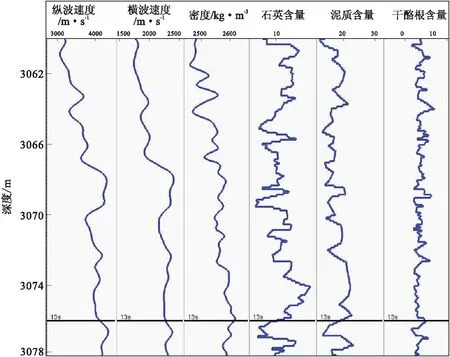
图3 L工区A井的测井曲线Fig.3 Well A logs of block L

图4 第三层裂缝介质参数Fig.4 Fracture parameter of the third layer(a)裂缝密度；(b)裂缝走向;(c)走向玫瑰图

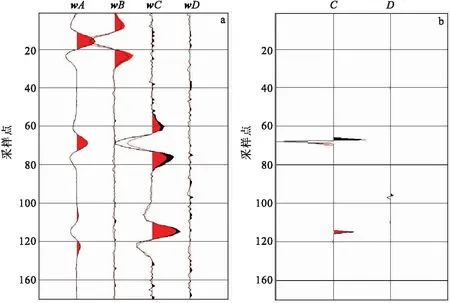
图5 反演结果(黑)与真实值(红)对比Fig.5 Comparison between inversion result (red) and real result (black)(a)第一步；(b)第二步

图6 反演结果Fig.6 Inversion result(a)各向异性梯度；(b)各向异性梯度方向；(c)方向玫瑰图

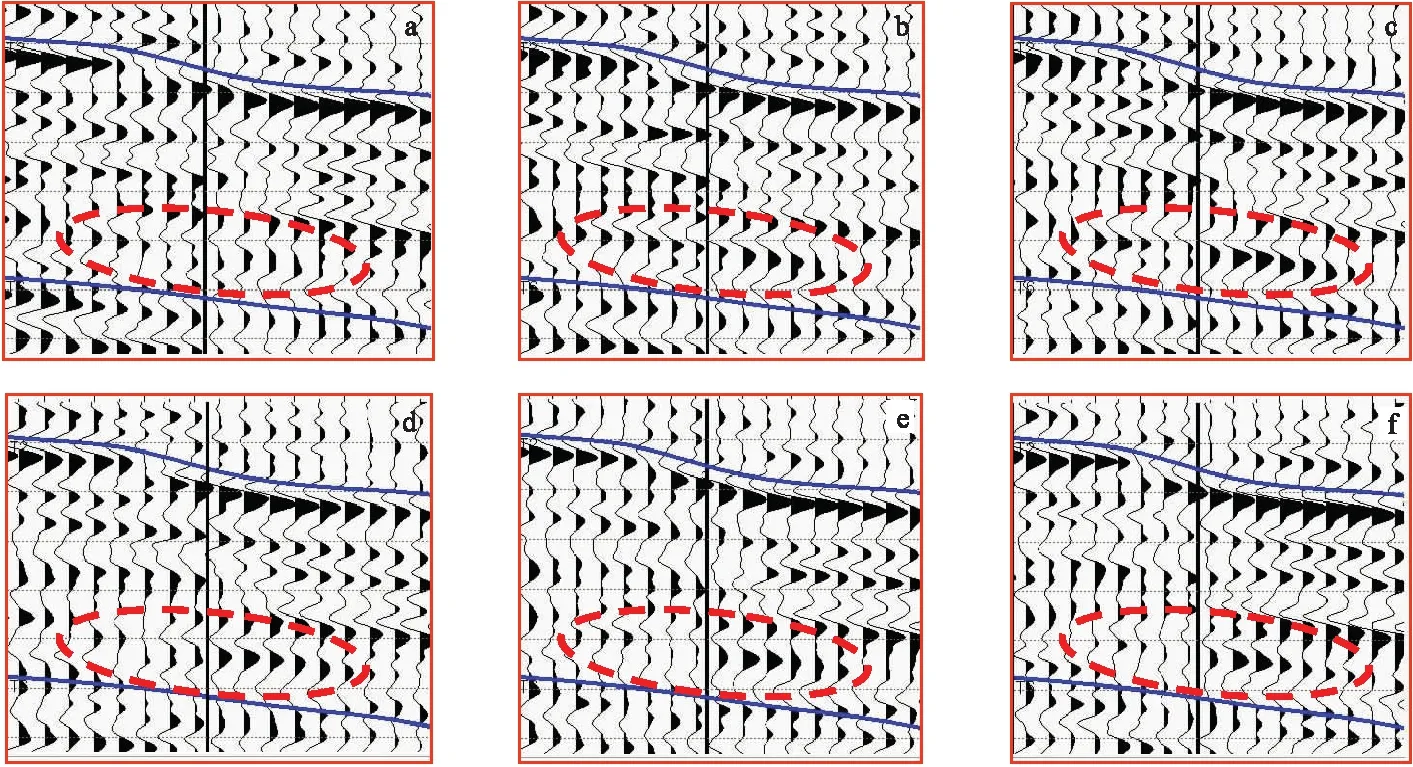
图7 不同方位叠后地震道集Fig.7 Post stack seismic of different azimuth(a)0°～30°;(b)30°～60°;(c)60°～90°;(d)90°～120°;(e)120°～150°;(f)150°～180°

图8 裂缝预测结果Fig.8 Fracture prediction results(a)各向异性梯度；(b)各向异性梯度方向玫瑰图；(c)测井结果

4 实际裂缝地层预测应用

利用某工区过A井的实际地震数据参与反演，该工区发育大段泥页岩裂缝地层，工区内地震、测井资料比较完备，适合于利用方位道集进行裂缝型储层预测研究。该方位地震数据的炮检距和方位角分布比较均匀，属于宽方位角地震数据，因此适合于利用方位道集进行裂缝型储层预测研究。通过地震资料处理，得到了6个部分方位叠加道集，分别是0°～30°、30°～60°、60°～90°、90°～120°、120°～150°、150°～180°(图7)，图7中红框内的裂缝发育区地震振幅随着方位角变化而变化，说明方位地震对裂缝有较好的响应。

图8是该工区S地层裂缝预测结果，已知A井在S地层附近存在裂缝，图8中反演的S地层各向异性梯度在A井附近存在异常，这与已知认识吻合。另外，反演的各向异性梯度方向与测井的裂缝走向结果一致。以上表明，这里研究的各向异性梯度反演方法能得到准确的地层各向异性梯度。

笔者发展的各向异性梯度无约束反演方法，在第一步子波移位中就能得到较好的反演结果，该步简单易操作且对地震资料分辨率要求不高。第二步去子波，利用模拟退火法搜索反射界面位置，对于调谐地层效果较差，因此适用于较厚的地层，实际应用需根据地震资料分辨率决定反演步骤。

5 结论

各向异性梯度对预测裂缝型储层具有十分重要的意义，利用宽方位地震数据可以反演各向异性梯度。常规的地震反演是对反演方程做加法，但是对于没有各向异性测井数据的工区，是难以增加测井低频约束的。针对这种情况，可以利用笔者发展的消除子波和降低反演方程维度对反演方程做减法的方法，得到稳定的反演结果。该方法分为两步：①子波移位简单易操作能得到相对裂缝发育区;②去子波能得到绝对裂缝发育区，但操作较为复杂且对地震资料分辨率要求较高。模型试算和实际工区应用表明，该方法能够得到准确的各向异性梯度，据此可以较为准确地预测高角度裂缝发育带，进一步可以为钻探裂缝型地层提供借鉴。