基于Delaunay三角剖分的二维交互建模研究

杨 强

(中国石化 石油物探技术研究院，南京 211103)

0 引言

地震勘探中，正演模拟不但在地震数据采集中得到应用，在地震资料处理和地震资料解释中也是重要的验证技术手段，是进行地震反演的基础。而正演模拟的基础就是需要准确且合理的地质模型，因此建模是地震正演的重要基础。传统上地质模型都沿用Cenveny提出的模型结构，即所谓层状结构模型。它要求每一个分界面都必须从模型体的左边界贯穿到模型体的右边界，分界面按顺序由上到下依序排列，不得交叉。对于逆断层、尖灭、透镜体等复杂地层情况，只能人为地简化模型，从而满足层状模型。

在实际的地球物理勘探中，层状结构模型有两个严重不足:①在采集、处理、解释各阶段的模型大都有逆断层、尖灭、透镜体等复杂地质元素,层状结构模型无法准确描述复杂的地质拓扑结构，从而无法得到网格化模型;②处理中的叠前深度偏移速度建模以及地震解释构造建模等，都要求能够交互修改模型，交互编辑中的层位修改及移动必须遵循层状规则，这对交互式复杂建模而言很困难，也不便利。蒋先艺[1]提出用点、段、线、面的概念描述二维封闭结构模型，实现了二维复杂地质结构，其优点是地震建模的数据层位、断层、透镜体都可以用点、线、面集来描述。这种方法比较复杂，难点就在于封闭块体的追踪。由于建模中的基本元素是点和线段，由这些基本元素需要得到地质结构的拓扑关系，采用三角剖分是一种理想的处理手段。

1 方法及思路

Delaunay 三角剖分是二维平面内的最优三角剖分，它在有限元分析、信息可视化、计算机图形学等应用领域有着重要应用[2]。Ruppert的二维高质量网格生成算法是第一个理论上保证网格划分算法在实践中真正令人满意的算法[3]。Refine Delaunay 三角化方法解决了保边界和内嵌边界的问题,该方法往往通过在保留边(约束边)上加入新的节点以实现保边界的目的[4]。笔者通过对Delaunay三角剖分的研究，以点和线段为基础，对层位、断层、透镜体进行三角剖分，采用封闭多边形结构描述复杂地质结构的拓扑关系，从而解决正演模拟建模中存在的问题。

1.1 方法分析：

经典的Delaunay三角剖分算法主要有两类：①Watson算法;②局部变换法。Watson算法又称为Delaunay空洞算法或加点法，从一个三角形开始，每次加一个点，保证每一步得到的当前三角形是局部优化的。Delaunay三角剖分加点算法采用点定位方法[5]。点法利用Delaunay空洞性质，简明地实现了三角剖分。这种方法的优点是在实现上比局部变换算法相对容易，而且与空间的维度无关。该算法在处理新点加入时，会重新计算三角形单元并判断其属性。如果包含新点的三角形单元不再符合Delaunay属性，则这些三角形单元被删除，形成Delaunay空洞，然后算法将新点与组成空洞的每一个顶点相连生成一个新边，根据空球属性可以证明这些新边都是局部Delaunay的，因此新生成的三角网格仍是Delaunay的[6]。

考虑到透镜体的网格化问题,这里采用了加点法的Constraint Delaunay[7]算法，利用其空圆特性和最大化最小角特性，先将模型的原始点集和边进行三角剖分，再结合文献[1]提出的二维复杂地质结构，利用原始(非添加)点集和线段集寻找封闭区域，从而形成系列的多边形来描述模型。

1.2 模型的三角剖分

Constraint Delaunay 要求处理的对象必须是PLSG(Planar straight line graph)，PLSG定义为点和线段组成的集合，要求每个线段的端点，应该在点的序列中，而端点由点的序号来标示。借鉴文献[1]的思路和Constraint Delaunay三角剖分，只要在前期处理中把层位、断层、透镜体等对象分解为点和线段集合就可以满足三角剖分的输入要求，而对于每次交互式修改，就相当于对离散点集和线段集合进行重构，从而克服了层状结构模型的限制约束。对模型进行Constraint Delaunay 三角剖分的步骤：

1)对原始输入数据处理，形成满足PLSG 图的点和线段的集合，采用加点法进行Delaunay 三角剖分。

2)恢复丢失的线段：用Constriant Delaunay 三角剖分，删除线段有重叠的三角形，在线段两侧重新进行三角剖分，以此确保在没有引进任何新点的情况下线段的恢复。

3)删除不必要的三角形。主要是删除“空洞”和“凹”处的三角形。三角剖分的计算量很大，这种处理有利于提高三角剖分的效率。

Lawson 算法还有一个步骤是保持三角剖分的Delaunay 性质。它通过插入新点，并对三角剖分进行细化，直到对三角形最小角和最大面积的限制条件满足[8]。保持三角剖分的Delaunay 性质本来是Delaunay三角剖分的一个核心，但本方法的目的在于形成封闭多边形结构，对于多边形的形状要求尽可能保持模型本身的形状，对于保持三角剖分的Delaunay特性没有特殊要求，因而在本方法的剖分中没有应用。同样，步骤2)也是为了模型的准确性以及减少三角化的计算量，采用不增加新点的方法，从而简化后面的封闭拓扑构成的工作。

1.3 形成封闭拓扑结构

模型三角剖分结果的结果是一系列的三角形，对于建模需要得到封闭体还需要基于三角剖分的结果(三角形集合)进行搜索，形成由原始边(线段)构成的封闭多边形，其步骤如下：

1)三角剖分后形成若干个三角形，标记不是原拾取点形成的边以及原拾取点所形成的边集合。

2)确定一个起始三角形，预定义一个多边形。

3) 将三角形的原拾取点和边添加到定义的多边形，并依据非原始边去找新的三角形，依次循环递归查找，直到无法找到非原始点的边。

图1 封闭拓扑结构流程Fig.1 Flow chart of closed topology

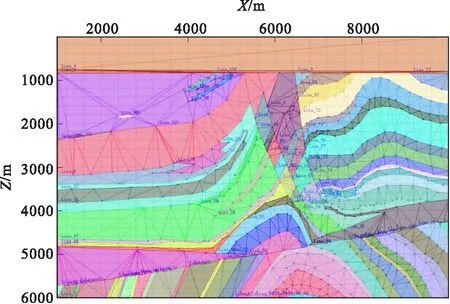
图2 Marmousi模型剖分及封闭结果Fig.2 Results of Marmousi model triangulation

图3 Marmousi原始速度模型Fig.3 Original Marmousi vp-model

4)利用上步记录的原始点边集合添加到多边形，可组成一个封闭多边形(未形成闭合就不纪录此多边形)。

5)查找没有用到过的另一个三角形，重复步骤3)、步骤4)，直到找完全部三角形。

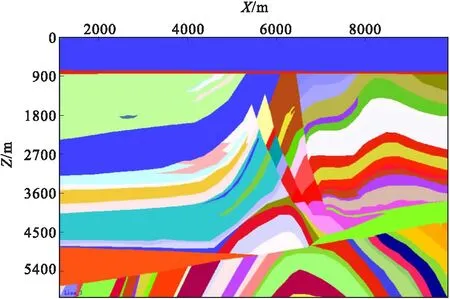
图4 Marmousi模型网格化结果Fig.4 Results of gridding Marmousi model

图5 网格模型正演结果Fig.5 One shot record of gridding Marmousi model

形成封闭拓扑结构流程图(图1)。

通过以上流程可以得到一系列的封闭多边形，在此基础上根据网格划分的步长，从道方向对网格点的坐标进行遍历，从而确定网格点位于属于哪个封闭多边形，这样就可以进行属性填充，完成模型的网格化从而得到正演所需的网格模型。

2 应用实例

利用本文方法，结合Qt.4.X(X>2)开发工具进行开发，形成了完整的实用软件，以下是具体实例。

2.1 Marmousi模型

Marmousi模型是地球物理经典模型，涵盖了大多数地质模型对象，图2给出了三角剖分结果、封闭结构结果(块状模型)。

图3是Marmousi模型的原始纵波速度模型，图4是由剖分结果按上述网格化方法填充属性后得到的网格化模型，对比图2与图3反映了剖分的准确性。通过图3和图4对比，反映了网格化结果满足建模的需求。

在模型中左边的3个狭长的复杂的透镜体，三角剖分时都被狭长的三角网覆盖，三角网内多边形保持了Delaunay特性反应了剖分算法的正确性，网格化结果也反映了寻找封闭区域算法的准确性。

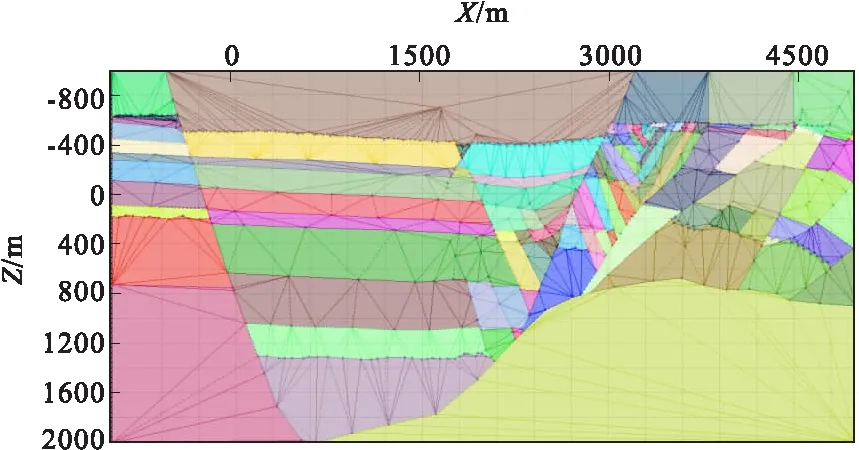
图6 实际模型剖分及封闭结果Fig.6 Results of real model triangulation

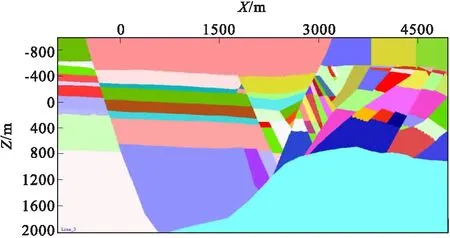
图7 实际模型网格化结果Fig.7 Results of gridding real model

由网格化的数据用iSeisWave(自研软件)软件进行正演模拟，激发点位于模型2 100 m处，最小炮检距为1 050 m，道间距为25 m，得到的单炮记录如图5所示，可见本方法能满足地震正演模拟的建模需求。

2.2 惠民凹陷盘河模型

此模型是勘探生产中的实际复杂模型，三角剖分结果和网格化结果如图6、图7所示。

图6、图7两个实例中都存在狭长三角形，就是因为三角剖分中省略了步骤4)-用Lawson 算法保持三角剖分的Delaunay 性质。图7中，中间及右边的大断层起点并没有与其他层位或断层相交，三角剖分正常，网格化时都因非闭合而被忽略，再次验证了形成封闭体算法的正确性。

通过实践，每次交互修改后形成PLSG，可以对模型进行重构——直接进行三角剖分，三角剖分及形成封闭多边形在三角网较大数量级(10×104级别)基本可以做到实时，对交互式建模提供了极大的便利(无需考虑层位和逆断层的控制问题)。同时在网格化步长较大(横向和纵向步长都为10 m)的情况下，经典模型和实际模型的网格化结果都达到了生成要求。

3 结论

笔者采用的基于三角网的建模方法突破了层状建模的局限性，同时比已有的块状建模方法更加简单，效率高。本方法不仅能建立块状模型，还能得到非结构化网格模型，因此有更好的应用前景，为地震勘探中复杂交互式建模提供了有效的方法。