基于改进的Morlet小波变换在伊犁盆地南缘层序地层划分中的应用

苗辰若,高晓伟

(核工业二一六大队，乌鲁木齐 830011)

0 引言

层序界面的划分和地层对比在地层评价工作中占有重要地位，正逐渐由定性走向定量、由宏观走向微观，其在砂岩型铀矿中有着广阔的应用前景[1-2]。相对于提取地震属性[3]，无论是纵向分辨率还是连续性，测井资料都是最好的一种地质资料，是对地层某个特定的物理参数随着深度变化的反映，包含的地质信息丰富，是当前进行地层划分与对比最成熟的手段。随着测井技术的进步，测井数据的地质属性为层序划分和地层对比方面的研究提供了很好的条件。通过对测井曲线的分析，可以将其包含的地质信息和地质属性直观地体现出来。

应用测井曲线进行基准面旋回划分，结果因人而异，原因在于测井曲线所反映的沉积序列，本质上是各个地质周期沉积响应的叠加，人为判断并划分地质周期会存在主观随意性。小波变换[4]可以从复杂多变的原始测井信号中识别提取出信号的时频特征，以多种尺度、多种分辨率对测井信号中的周期成分进行探测[5]。传统的Morlet小波在地球物理数据处理、地质属性提取等方面较其他小波分析方法有优势，但其不满足小波的容许条件，无法对处理信号进行逆变换，所表达的地质、地球物理信息仍然较为模糊。通过对传统Morlet小波进行改进，并利用改进后的Morlet小波，将一维测井信号转换为二维深度-尺度信息，通过振幅谱和相位谱信息有效地识别旋回类型、层序地层界面，取得了较好的效果。

1 小波变换

1.1 原理

小波是一个衰减的波形，它在有限的区域里存在(不为“0”)，并且其均值为“0”。

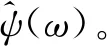
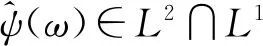
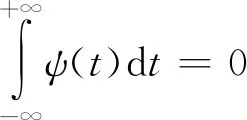
(1)

(2)

式中：ω为角频率；ψ(t)为一个基本小波(小波基)或母小波(Mother Wavelet)，式(1)被称为容许条件，也被称为容许小波。

Cf(a,b)=〈f,ψa,b〉=

(3)

式(3)被称为f以ψ为基的小波变换。

对小波基进行伸缩平移变换，得到一个小波函数簇，如式(4)所示。

a,b∈R,a≠0

(4)

式中：a为尺度参数;b为时间平移参数；ψa,b(t)为小波基函数。当a、b时连续变量时，称之为连续小波变换(CWT)。

小波变换的示意见图1。由图1看出，小波变换可给出各个时刻由不同尺度和不同位置的小波构成的信号。

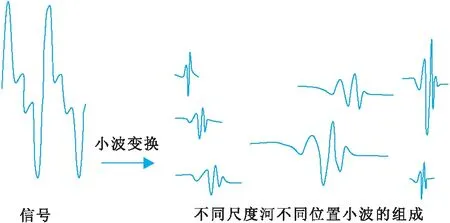
图1 信号小波变换示意图Fig.1 Schematic diagram of signal wavelet transform

从本质上看，小波变换本质上是一种积分变换，包含两个参数(尺度参数、时间平移参数)，经过小波变换后，时间函数被投影到二维的时间-尺度平面上，可用来更好地分析周期特征。

图2为某钻孔测井信号经Morlet小波变换后的尺度参数图。同一个沉积周期的测井曲线经小波变换后的小波系数具有了相同的振荡幅度，不同尺度的小波变换实现由粗到细分级别的层序划分奠定了基础。尺度参数与地层沉积周期和频率对应，①大尺度对应低频、长周期的地层，可用于划分大的层序地层；②用中等尺度代表中等周期的地层层序；③小尺度对应高频、短周期的沉积地层，由于层序级别越小，内部的自旋回沉积现象越多，对层序旋回的干扰也就越大，对于这种级别的层序，不能用高频部分确定。

1.2 最优小波的选取

运用较多的小波有Daubechies(Db)小波、Morlet小波、Meyer小波等几种，每种小波的函数和形态有所不同，所有满足小波条件的函数都可以作为小波函数。

实际应用中选择小波类型的原则主要有3种[7]：

1)自相似性原则。若选择的小波对信号有一定相似性，则变换后的能量比较集中，可以有效减少计算量。

2)判断函数。针对特定的问题找到关键性的技术指标和参数，得到的函数即判断函数，然后再将各种小波函数代入，得到最优函数。

3)支集长度。大部分应用选择支集长度为5 m～9 m的小波，避免支集太长产生边界问题、支集太短不利于信号能量集中。

实际应用中测井数据包含的信息非常丰富，且数据体比较大，不存在万能模式。不同工作地区和地质条件不同，选择的小波类型也必须通过该工作区典型钻孔的小波分析结果与地质资料的反复对比来确定。目前已有较多的研究[7-8]使用测井曲线的小波变化进行沉积旋回的划分。

Morlet小波不具有正交性的同时也不具有紧支集，其在时间-频率域上分辨率很高，其实部和虚部之间的相位偏移为90°，可以方便地获取信号的瞬时频率和瞬时相位等信息[9-11]，在划分沉积旋回时具有更好的适用性。

1.3 Morlet小波的改进

以Morlet为核函数的小波变换将时间域信号转换到时间-尺度域时，需要通过基本小波的中心频率和小波尺度这两个参数来计算并获取小波的中心频率[12]，这将使小波参数的物理含义不能被清晰表达。

图2 不同尺度参数下GR曲线的小波变换系数Fig.2 Wavelet transform coefficients of GR curve under different scale parameters

Morlet小波函数的基本公式为式(5)。

(5)

为了使小波基的参数选择具有一定的自适应性，引入带宽参数k2，提出以下的Morlet小波函数对信号进行小波变换：

(6)

将其代入公式(1)，得到

(7)

很明显Morlet并不满足小波的容许条件，因此也就不存在Morlet形式的重构公式或者逆变换公式。

当ω0≥5或者k2≥2时，上述积分值随着或的增大而迅速减小，可忽略不计，此时Morlet函数接近满足容许条件。据此，对式(6)进行了改进，取ω0=2π,得到改进后的小波函数：

(8)

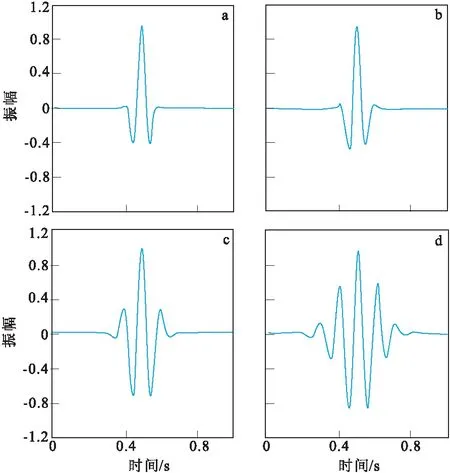
图3 不同k2值Morlet小波波形Fig.3 Morlet wavelet waveforms with different k2 values(a)k2=1/4;(b)k2=1/3;(c)k2=1/2;(d)k2=1/1

分析Morlet小波发现，随着值的增大，小波时域包络线逐渐逼近余弦函数的某一段。小波时域持续期越长，频率域小波滤波器带宽越窄，抗噪性能越好，但增大值要受到容许条件和时域分辨率降低的限制，因此，对于Morlet小波而言，最佳的值需要根据具体情况来选择。根据图3中时域分辨率的表现以及多次测井数据试验，本次设定值为1/2，既增强了有效信号的分辨率，又能避免振幅宽度过大影响临近信号。

改进后的Morlet小波变换有以下几个优点：①将信号从时间域映射到时间-频率域；②小波各个参数有了明确的物理意义；③进行逆变换更加简洁方便。

修改MATLAB小波分析工具箱Morlet小波基函数源代码为：

function [out1,out2] = morlet(LB,UB,N,flagGUI)

out2 = linspace(LB,UB,N);

out1 = cos(-2*(out2.^2)) .* exp(2*pi*out2);

1.4 测井曲线的选择

由于不同测井曲线会蕴含着不同的地质意义，若采用相同的函数和参数进行变换，可能会得到不同的结果。在研究中对GR、SP以及密度等多条测井曲线数据进行小波分析后发现，虽然得到的曲线形态上不一致，但对沉积周期的划分基本一致(图4)。

沉积岩地层中的自然伽马曲线(GR)在高频部分和低频部分都包含有更丰富的信息，周期响应明显，相对于密度曲线和自然电位曲线更能体现泥质含量的变化。利用其进行层序界面划分与地层对比具有明显的优势，也是最有效的方法[13]。因此，笔者采用自然伽马测井曲线进行分析。

2 小波信号的地质属性

自然伽马曲线的小波信号包含的2个地质属性：砂/泥含量沿垂向的周期变化规律、频率变化规律[14]。通过自然伽马曲线的小波变换能够快速-准确地获得砂/泥含量和砂泥互层频率，这是地层层序划分的两项重要指标，同时也是确定陆相盆地基准面旋回周期和划分层序的重要依据。

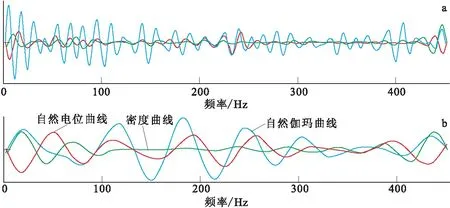
图4 不同测井曲线的Morlet小波分析结果Fig.4 Results of Morlet wavelet analysis of different logging curves(a)高频部分;(b)低频部分

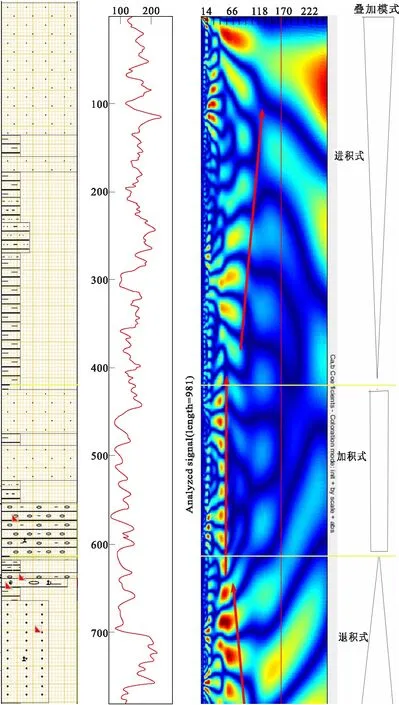
图5 旋回叠加模式的GR曲线连续小波振幅谱分析Fig.5 Continuous wavelet amplitude spectrum analysis of GR curve of cyclic superposition model

利用Morlet小波基函数对自然伽马测井信号进行1:1:256尺度小波连续分析，得到振幅图谱(图5)。在图5中，能量的交替变化对应着砂泥岩互层沉积的变化。振幅谱能量的偏移方向对应着砂泥岩薄互层的厚度变化规律；能谱带尺度的偏移对应着由净沉积速率的变化引起的旋回逐渐增厚或减薄的变化。从下而上分析，能谱带尺度偏小，表明相对水体上升，沉积速率减小、旋回厚度减小、砂/泥比变小，体现了退积式旋回的岩性变化特点，呈下粗上细正旋回；能谱带尺度稳定，说明各旋回的厚度基本稳定、砂/泥比相同、体现了加积式旋回的岩性变化特点；谱带尺度偏大，则反映了相对水体下降、沉积速率增加、旋回厚度增加、砂/泥比变大，很明显的体现了进积式旋回的岩性变化特点，呈下细上粗反旋回。

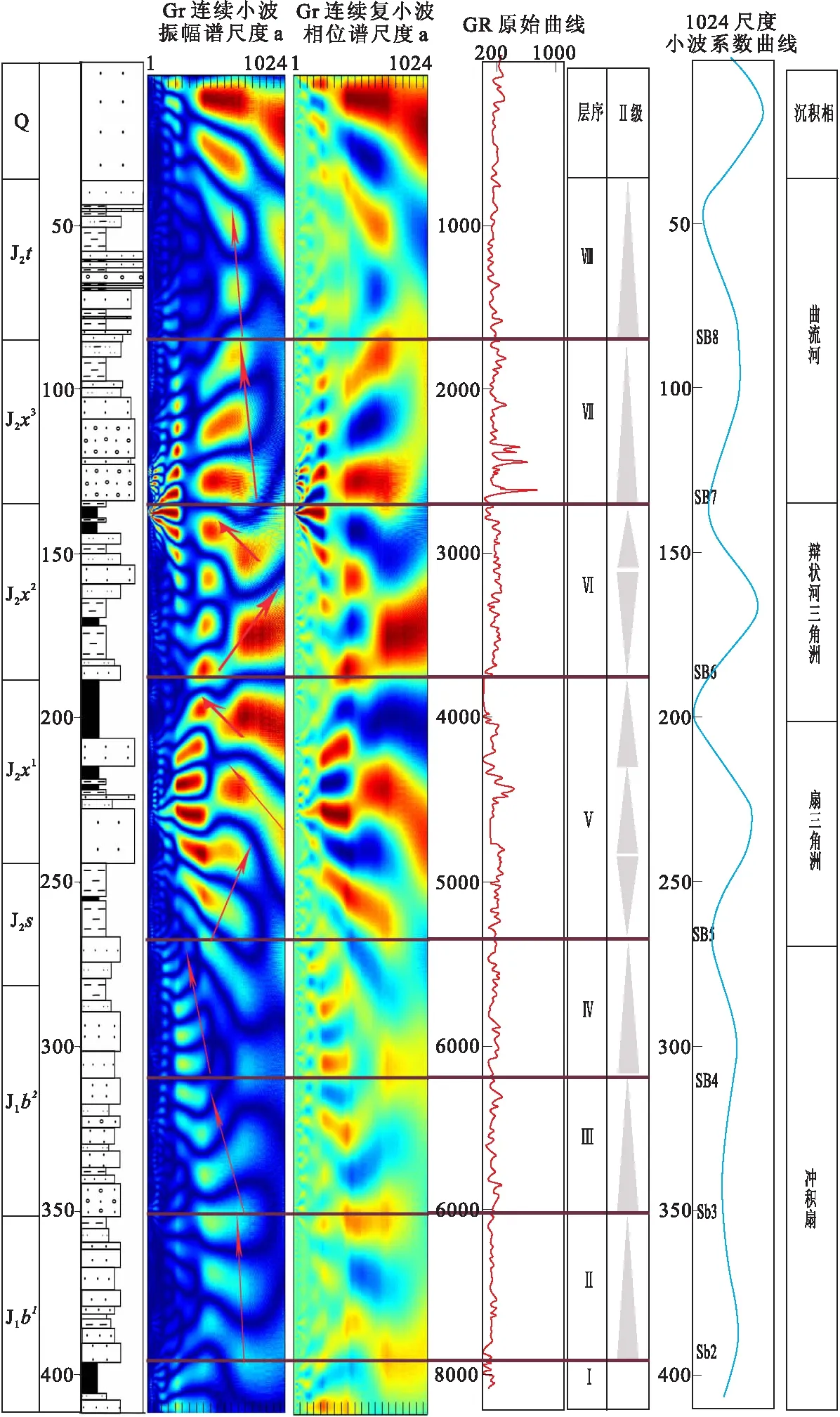
图6 A4560孔Morlet一维连续小波振幅谱图像Fig.6 Morlet one-dimensional continuous wavelet amplitude spectrum image of hole A4560

3 实际测井地层应用分析

3.1 区域地质概况

伊犁盆地南缘中下侏罗统水西沟群不整合上覆于三叠系，为一套在潮湿气候条件下形成的、总体表现为退积特征的冲积扇-扇三角洲-曲流河沉积体系下形成的暗色含煤碎屑岩建造[15]。

该区地层较稳定，层理构造以水平层理为主，垂向充填序列的规律性周期变化，与基准面的波动是同一趋势的。砂/泥比变化规律体现了三角洲的进退或者湖泊的扩张、收缩。

此次选取了最具代表性的苏阿苏地区A4560钻孔侏罗系地层进行研究。

3.2 应用实例

3.2.1 小波分析结果

对自然伽马曲线采用Morlet小波基进行一维连续小波分析，获得了1:1:1024尺度小波振幅谱图像(图6)。

由于连续小波相位谱可以较好地识别层序级次及湖泛面位置，笔者对相位谱进行了计算并参考。

根据连续小波振幅谱和连续复小波相位谱划分出划分了7个层序界面(SB2-SB8)。

层序界面在相位谱上位于相位零点，不整合界面表现为弯曲的零线。振幅谱能谱带位于界面上下存在突变现象，反映了沉积环境与沉积速率的变化。相转换面的相位零线为直线形态，在振幅谱能谱带上位于进积式旋回或退积式旋回的转化处。

3.2.2 地质解释

通过小波分析，在A4560孔划分了8个不同叠加模式的旋回(Ⅰ～Ⅷ)，以退积式旋回为主，仅Ⅴ1、Ⅵ为进积式旋回:

八道湾组(J1b)地层分为上、下两段，四个旋回(Ⅰ～Ⅳ)。每个旋回均由下部粗粒段(砂体)和上部细粒段组成，具有下粗上细的正韵律特征。其中下段两个旋回(Ⅰ～Ⅱ)中，Ⅰ旋回发育有一层较厚的煤层，煤层下伏泥岩和细砂岩。Ⅱ旋回以粗砂岩占优势夹有多层泥岩、粉砂岩，砂/泥比值较高，具有典型的冲积扇扇中特征。上段的Ⅲ旋回粗粒段以粗砂岩、砂砾岩为主，砂/泥比值最高，具有冲积扇扇根特征。Ⅳ旋回以粗砂岩为主，砂/泥比含量下降，顶部的泥岩和粉砂岩具有扇端特征。由此可看出，八道湾期基准面经历了较长时期的上升过程。

三工河组(J1s)地层对应Ⅴ1亚旋回，岩性以泥岩为主，顶部覆盖西山窑组的粗砂岩，无过渡沉积环境，呈断陷湖盆扇三角洲常见进积型向上变粗的反韵律序列。

西山窑组下段(J2x1)地层以扇三角洲沉积为主，对应Ⅴ2亚旋回，扇中主体为粗砂岩和中砂岩，呈正韵律，基准面上升半旋回的顶部为扇端洼地，发育多组煤层。

西山窑组中段(J2x2)地层的岩性变化较为规律，岩性为粗、中砂岩-粉砂岩-泥岩-煤层，共两组，对应Ⅵ旋回，包含一个完整的水退-水进周期，基准面下降半旋回时期略长于上升半旋回。岩性结构上，具有辫状河沉积的假二元结构特征，其水平、波纹层理构造以及煤层的存在，说明该地层为湿润气候下的河漫沼泽沉积亚相。

西山窑组上段(J2x3)对应Ⅶ旋回，岩性由下向上为灰色含砾砂岩、砂岩、粉砂岩和泥岩，可分为四个沉积单元，砂/泥比接近1:1，基本上呈正韵律，韵律分为上下两段，具有典型的二元结构特征，为曲流河相沉积。

头屯河组(J2t)对应Ⅷ旋回，上伏于中侏罗统水西沟群，岩性主要为褐黄色、紫红色的杂色碎屑岩沉积，其上部多为泥岩、中细砂岩互层，发育水平层理，底部以中粗粒砂岩为主，发育块状构造、交错层理，可见薄煤层。该旋回曲流河沉积相和辫状河沉积相特征均不明显，暂划分为曲流河相沉积。

3.3 结果对比

采用该方法流程对苏阿苏地区A4560、A4904、L29207、L34064孔进行了层序划分，与地质报告中的划分结果对比见表1。

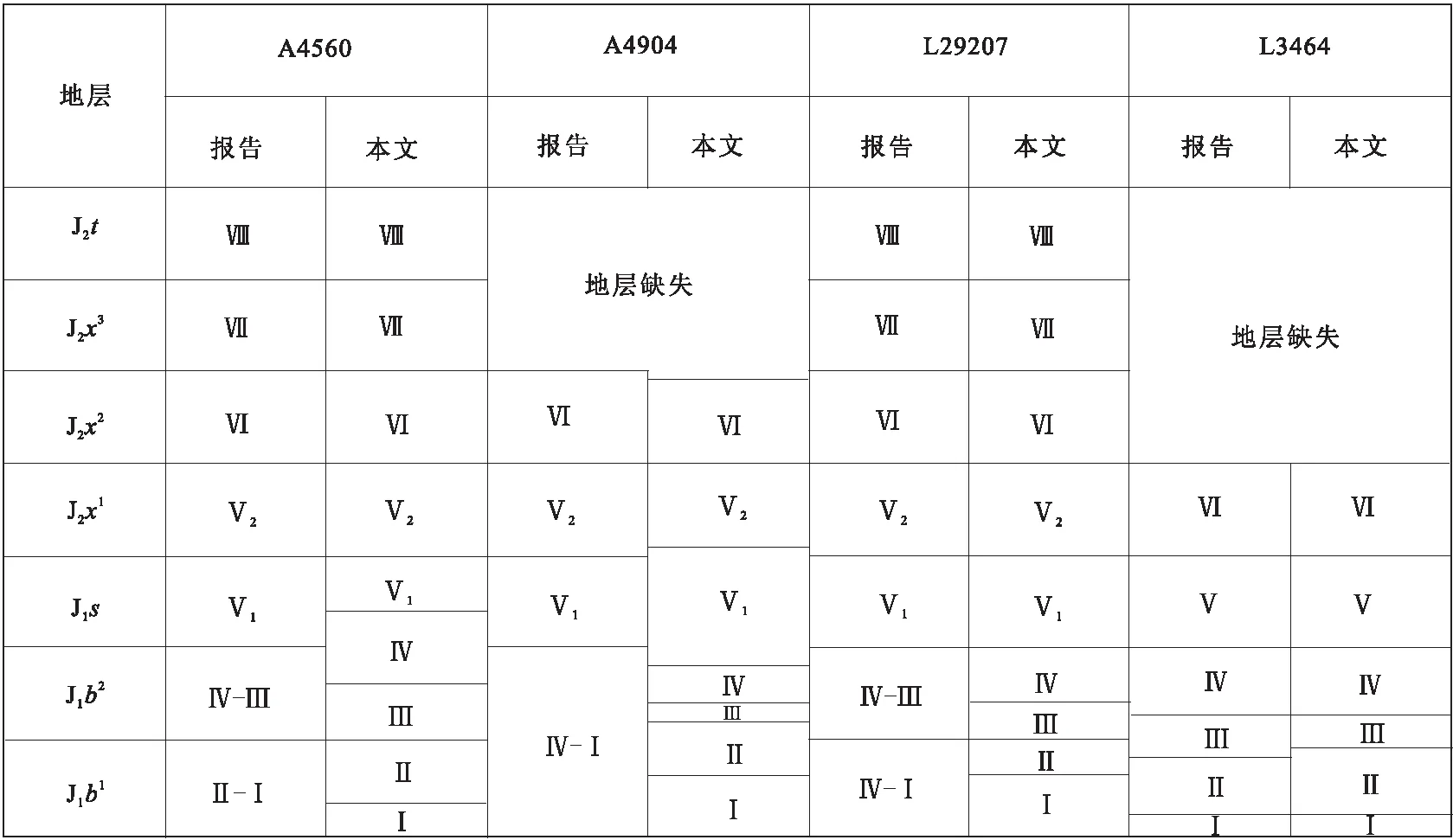
表1 各钻孔层序划分结果对比Tab.1 Comparison of sequence division results of each borehole

通过表1可以看出，利用该方法划分的层序与岩性岩相+电性分析法划分的层序基本相同，除A4560、A4904孔在Ⅳ、Ⅴ旋回界面略有差别，其余界面基本吻合。

4 结论

在传统Morlet小波变换的基础上，引入参数对带宽进行控制，使得小波函数的表达形式更加灵活，在物理学和地质学上的意义表达更清晰。

利用改进的Morlet小波变换，对自然伽马测井曲线进行连续小波振幅谱和复小波相位谱特征分析，实现周期级别、旋回类型、层序界面的识别和划分，对于不同类型的层序界面，其振幅谱和相位谱响应特征有明显区别。与传统的地层层序划分手段相比，该方法能更加有效地利用自然伽马测井数据的内部结构信息，准确的识别层序界面，为层序划分提供更加可靠的依据。