例谈解析几何若干活动经验的优化与重构

李永革

(安徽省巢湖市第一中学 238000)

经验是影响数学发展和数学学习的一个重要因素，数学的认识归根结蒂来自经验、来自实践.经验在数学教育中的积极作用正在被人们所重视.但是，经验在数学教学中的消极作用却容易被忽视.杜威指出：“每一种经验就是一种推动力，经验的价值只能由它所推动的方向来评断.相信一切真正的教育是来自于经验的，这并不表明一切经验都具有真正的或相同的教育性质，不能把经验和教育直接地彼此等同起来.因为有些经验具有错误的教育作用”.

本文列举学生在解析几何学习中若干活动经验的常见误区，提出优化的建议.

一、“设而不求”经验的优化

本活动经验来自于直线与圆锥曲线相交的背景下，处理弦长、中点弦、垂直等问题时对交点坐标只设不求，运用韦达定理整体代换，交点坐标起到几何特征代数化的过渡作用，可有效减少运算量.学生对本活动经验的常见误区有：

(1)只能在直线与曲线相交的情况下才能运用，在相切等其他位置关系下不能运用;

(2)只能用韦达定理整体代换消去坐标参数;

(3)直线与圆锥曲线相交，交点坐标只能设，不能求.

教学中可通过典型例习题的剖析与训练，让学生经历“设而不求”经验的优化、重构过程.

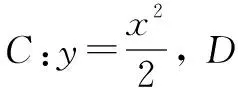
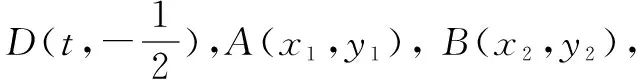
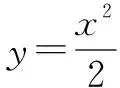
整理，得2tx1-2y1+1=0.

同理可得2tx2-2y2+1=0.

故直线AB的方程为2tx-2y+1=0.

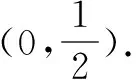
解题反思本题用到了“设而不求”的方法，但直线与抛物线的位置关系不是相交，而是相切.本题不是依靠韦达定理来消去切点坐标，而是利用过两点的直线的唯一性与曲线方程的定义(坐标满足方程，则点在曲线上).

经验优化“设而不求”的解题方法既可以用在直线与曲线相交的情形，也可用在相切的情形.

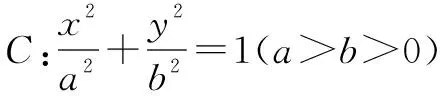
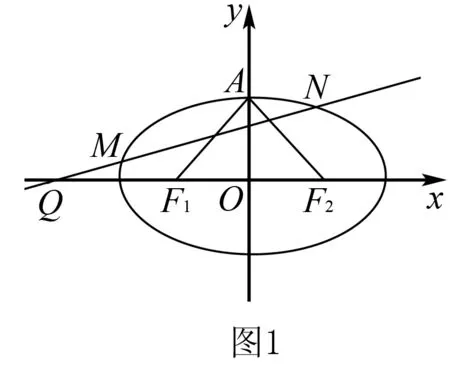
(1)求椭圆C的方程；

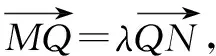
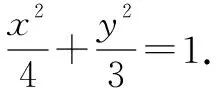
(2)设M(x1,y1)，N(x2,y2)，R(x0,y0)，

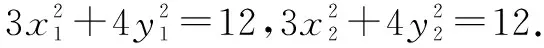
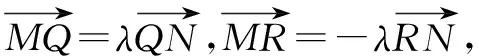
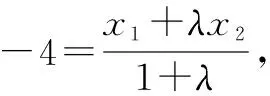
①

②

③

④

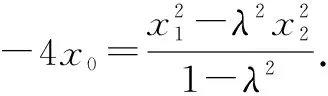
⑤

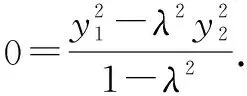
⑥

⑤×3+⑥×4,得

解得x0=-1，故点R在定直线x=-1上.

解题反思本题也运用了“设而不求”的解题方法，但消去坐标参数的方法不是运用韦达定理，而是利用点在椭圆上，点的坐标满足椭圆方程.

经验优化运用“设而不求”的解题方法时，消去交点坐标的方法不只是韦达定理，还有“点差法”“代入方程消元”“代入方程凑常数”等.

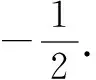
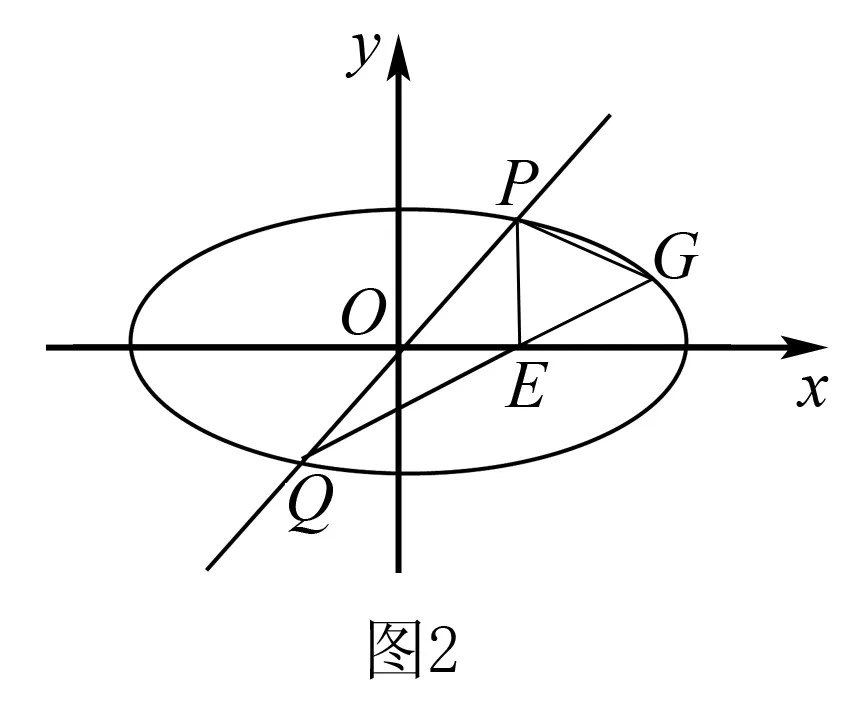
(1)求C的方程，并说明C是什么曲线；

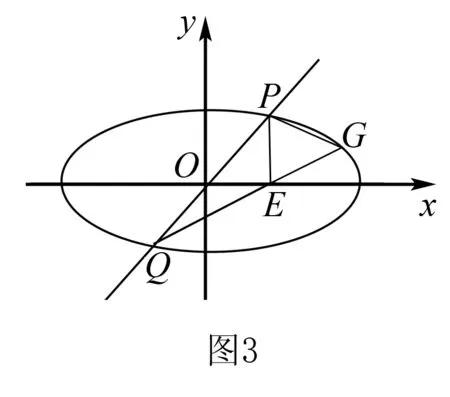
(2)过坐标原点的直线交C于P，Q两点，点P在第一象限，PE⊥x轴，垂足为点E，连接QE并延长交C于点G.证明：△PQG是直角三角形.

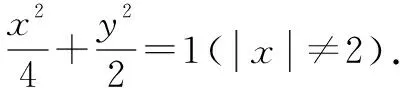
(2)设直线PQ的斜率为k，则其方程为y=kx(k>0).

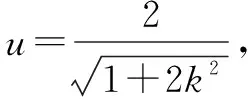
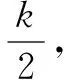
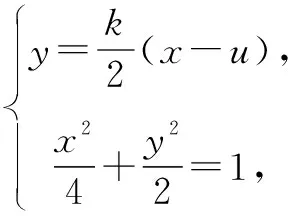
得(2+k2)x2-2uk2x+k2u2-8=0．

①

设G(xG，yG)，则-u和x2G是方程①的解.

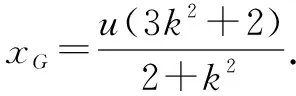
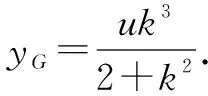
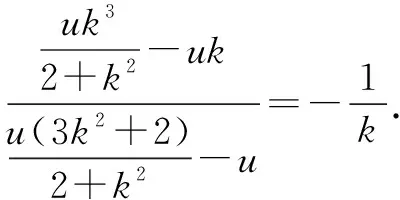
所以PQ⊥PG，所以△PQG是直角三角形．

解题反思题中直线PQ与椭圆相交，但由于它经过原点，故PQ的方程较为简洁，与椭圆方程联立求交点坐标并不繁琐.直线QG也与椭圆相交，但由于其中一个交点Q的坐标“已知”，故点G坐标也求出来了.考虑到交点P，Q的横坐标里含有根式，比较复杂，解题中采取“换元”，暂缓代入的解题策略减少了运算量，完成了证明.

经验优化当直线过原点或直线与曲线其中一个交点坐标已知时，求直线与曲线交点坐标并不麻烦，可以设而求.

二、“合理引参”经验的优化

参数思想是辩证思维在数学中的反映，一旦引入参数，就可用参数来表示点的坐标与线的方程的系数，从而刻画点与线的运动变化，将参数视为常量，以相对静止来控制变化，实现变与不变的转化.参数在解题过程中可将其消去，起到设而不求的效果.

参数法在求动点轨迹、定点、定值、最值、探索性问题中应用广泛.但如何引参，学生往往感到棘手，经验不足.常存在以下误区：

(1)参数越少，运算量越小；

(2)必须根据图形变化的根源选择参数.

教学中可通过对以下典型问题的思考与解答积累合理的引参经验.

例3(2019全国Ⅱ卷理21)第(2)小题.

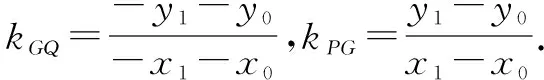
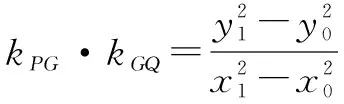
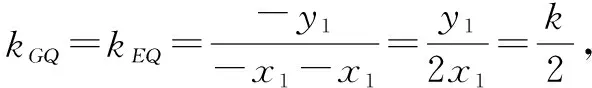
进而有PG⊥PQ,所以△PQG是直角三角形.

解题反思解法2与解法1相比，增加了参数的个数(从1个增加到5个，分别是x1，y1，x0，y0，k)，快速找到了线段PQ与PG的斜率关系，大大减少了运算量.

经验优化参数的个数并非越少越好.

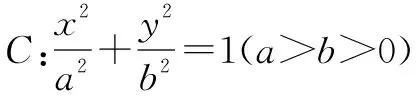
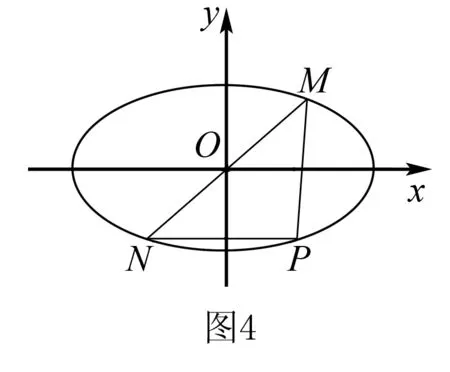
(1)求椭圆C的方程；

(2)设M,N是椭圆上关于原点对称的两点，椭圆上一点P满足|PM|=|PN|，试判断直线PM,PN与圆C′的位置关系，并证明你的结论.

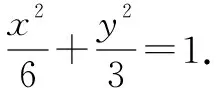
(2)因为M,N关于原点对称，|PM|=|PN|，

所以OP⊥MN.

设M(x1，y1)，P(x2，y2)，当直线PM的斜率存在时，设直线PM的方程为y=kx+m.

由直线和椭圆方程联立，得x2+2(kx+m)2=6.

即(1+2k2)x2+4kmx+2m2-6=0.

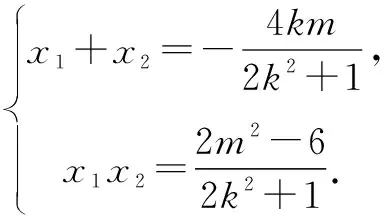
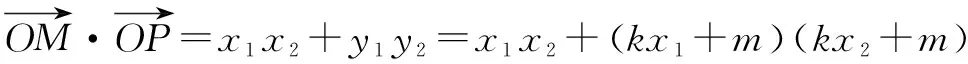
=(1+k2)x1x2+km(x1+x2)+m2

所以m2-2k2-2=0,即m2=2k2+2.

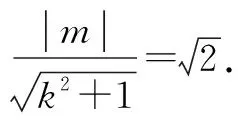
所以直线PM与圆C′相切.

当直线PM的斜率不存在时，依题意，得N(-x1,-y1),P(x1,-y1).

由|PM|=|PN|，得|2x1|=|2y1|.

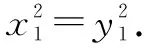
所以直线PM与圆C′也相切.

同理可得，直线PN与圆C′也相切.

所以直线PM,PN与圆C′相切.

解题反思从考情分析发现，大多数学生解答时选择直线MN的斜率k作为参数，然后联立直线MN与椭圆C的方程求出M、N两点坐标(用k表示)，再用两点式求直线MP的方程(用k表示)，最后用点到直线距离公式求点O到直线PM的距离并与圆C′的半径作比较，结果运算量过大，无功而返.这种思路显然受到前面所说的“经验”影响.从图形运动的根源出发选择参数，又想让参数数量最少，将图中点的坐标与直线方程都用唯一的参数k来表示，结果造成式子复杂、运算繁琐.解法1改设直线MP的斜截式方程(即引进直线MP的斜率与纵截距作为参数)，巧妙地解决了点O到直线PM距离难求的问题.

经验优化参数的选择往往是通过设点或设线的方式实现的，到底选择谁？选几个？前面所说的两个“经验”确实具有较为广泛的适用性，但不能绝对，一切要从思想方法的高度思考问题，以运算简洁为标准.不能模式化思考，过于教条.

三、“选系建系”经验的优化

建系求曲线方程是解析几何两大基本问题之一.坐标系建得好，可使方程推导的过程简单，方程的形式简洁，为下一步利用方程研究曲线性质奠定基础.学完解析几何之后学生一般都积累了一定的建系经验.都知道利用图形自身的对称性建系，利用图中垂直关系建系，若已知定点或定直线，知道将定点与定直线放在坐标轴上.但是学生在选系、建系上往往局限于建立直角坐标系，很少考虑其它坐标系，这样会影响学生解决问题能力的提高.

例4(合肥市2020年高三一模理20)

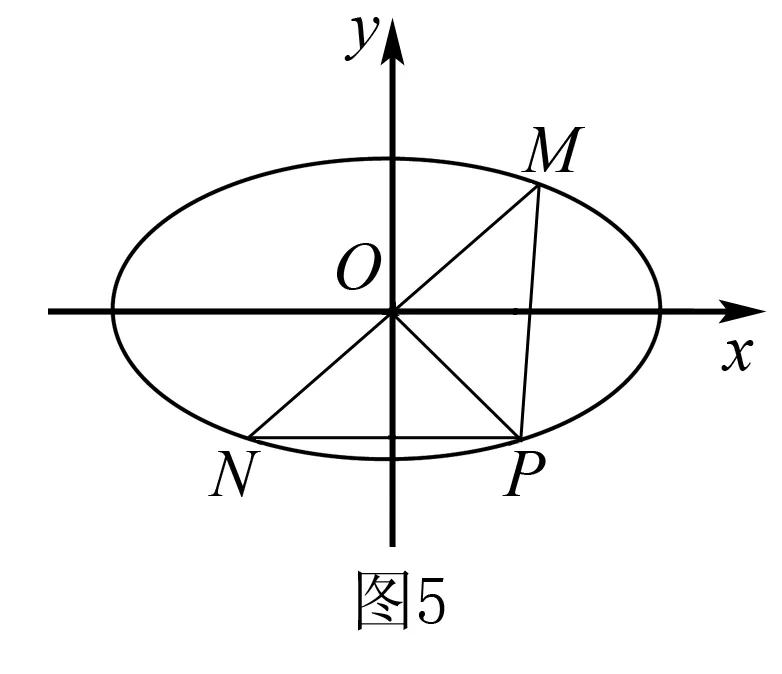
解法2由题意可知点P在弦MN的中垂线上，所以OM⊥OP，以O点为极点，x轴非负半轴为极轴建立极坐标系，则椭圆C的极坐标方程为ρ2(1+sin2θ)=6.

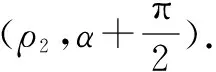
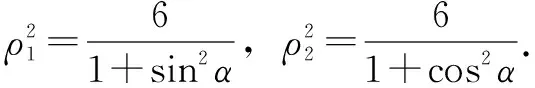
所以点O到PM的距离为

所以PM与圆C′相切.

解题反思解法2在计算点O到直线PM的距离时利用了线段OP和线段OM的长度，而这两条线段都是从原点O点出发的线段.考虑到P、M是椭圆上的点，故可用椭圆的极坐标方程快速求出OP、OM的长度.

经验优化当已知条件或结论涉及从某点出发的几条线段长度时，可考虑以该点为极点建立极坐标系，求出曲线的极坐标方程.

四、“弦长公式使用”经验的优化

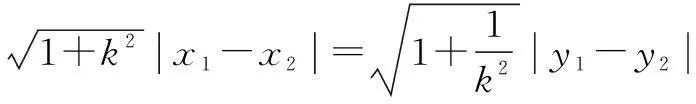
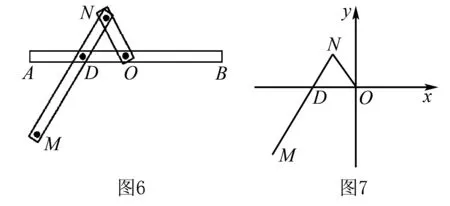
例5(2015年湖北，21)一种作图工具如图6所示，O是滑槽AB的中点，短杆ON可绕O转动，长杆MN通过N处铰链与ON连接，MN上的栓子D可沿滑槽AB滑动，且DN=ON=1，MN=3.当栓子D在滑槽AB内做往复运动时，带动N绕O转动一周(D不动时,N也不动)，M处的笔尖画出的曲线记为C.以O为原点，AB所在的直线为x轴建立如图7所示的平面直角坐标系.

(1)求曲线C的方程;

(2)设动直线l与两定直线l1:x-2y=0和l2:x+2y=0分别交于P，Q两点.若直线l总与曲线C有且只有一个公共点，试探究:△OPQ的面积是否存在最小值？若存在，求出该最小值；若不存在，说明理由.

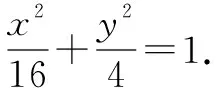
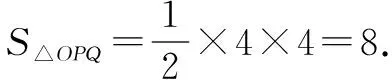
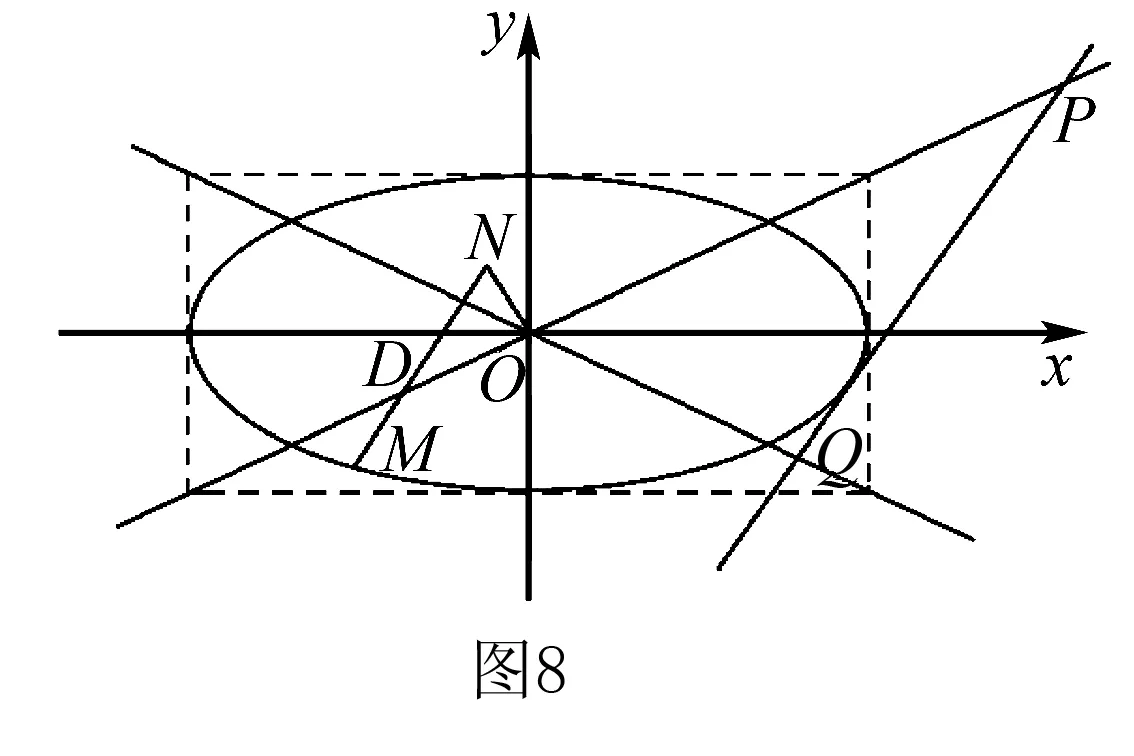
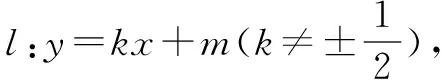
(1+4k2)x2+8kmx+4m2-16=0.

因为直线l总与椭圆C有且只有一个公共点，

所以Δ=64k2m2-4(1+4k2)(4m2-16)=0.

即m2=16k2+4.

①

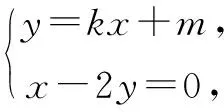
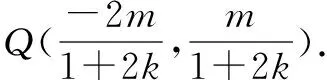
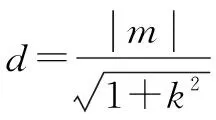
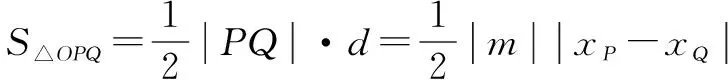
②

将①代入②，得

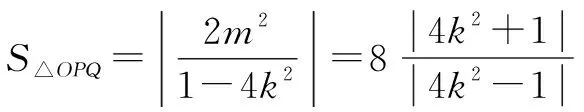
解题反思本例中斜线段PQ并非弦，但它的长度依然可用弦长公式计算.

经验优化弦长公式不仅可以求直线与圆锥曲线相交所得弦的长度，而且可以求坐标平面内其它斜线段长度.