基于ABAQUS的同刚度非接触式平面涡卷弹簧性能分析
冉江南,戴广永,曹子振,杨涛,白春生
基于ABAQUS的同刚度非接触式平面涡卷弹簧性能分析
冉江南,戴广永,曹子振,杨涛,白春生
(天津航天机电设备研究所,天津 300458)
根据经验公式,在同截面情况下非接触式平面涡卷弹簧的扭转刚度仅与其有效长度有关。本研究建立了一组同刚度非接触式平面涡卷弹簧的数学模型,基于ABAQUS仿真分析软件对各平面涡卷弹簧进行了有限元建模和分析;同时,将各平面弹簧的扭转刚度和工作应力的仿真分析结果与经验公式计算结果进行了对比,并在扭转刚度对比中引入了试验数据。结果表明,同刚度条件下,随着圈数的增大、节距的变小,基频明显变大、最大工作应力小幅下降、应力沿长度方向的波动变小、分布更加均匀。对比扭转刚度和最大工作应力仿真结果和经验公式计算结果,两方法之间存在一定的差异。
非接触式;平面涡卷弹簧;ABAQUS;有限元仿真分析
非接触式平面涡卷弹簧(以下简称平面涡卷弹簧)一般是用细长等截面金属材料在平面上绕制成的螺旋状弹簧,一般为机构提供反作用力矩或驱动力矩[1],广泛应用于中压开关、微电机、卫星铰链类机构等领域[2-3]。根据平面弹簧经验公式,在相同截面情况下,平面弹簧的刚度、应力(相同转角)等仅与平面弹簧有效长度有关。本文基于ABAQUS有限元仿真分析软件,分析了在理论同刚度(同截面)情况下,不同圈数、节距的平面弹簧的模态、刚度、应力等性能的差异性;同时,对各平面弹簧的扭转刚度和最大应力的仿真分析结果与经验公式计算结果进行了对比。
1 数学模型建立
根据弹簧相关手册和标准,平面涡卷弹簧有如下公式[4-6]:

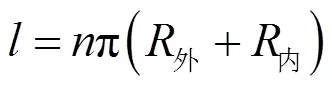
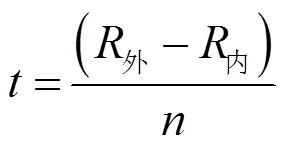

式中:为扭转刚度,N·m;为材料的弹性模量,MPa;为截面厚度,mm;为截面宽度,mm;1为经验系数,外圈转动时取1.25、外圈固定时取1;为有效长度,mm;为有效圈数;外为外圈半径,mm;内为内圈半径,mm;为节距,mm;为Mises应力,MPa;为变形角度,rad。
通过上述公式可知,在同截面的情况下,平面涡卷弹簧刚度仅与有效长度有关、最大应力仅与有效长度和转角有关。
设定平面涡卷弹簧的参数如表1所示,其中,涡卷弹簧的宽度、厚度、内径、有效长度均保持不变,仅改变圈数和外径,并对节距进行相应调整。

表1 仿真分析用平面涡卷弹簧参数
2 有限元模型建立
涡卷弹簧模型采用阿基米德螺旋线方程,如式(5)所示,在Creo里建立平面涡卷弹簧的三维模型[7-8]。由于研究重点在于不同节距的同刚度平面涡卷弹簧的性能研究,不关注内外圈连接形式,因此对模型进行适当简化,最终建立模型如图1所示。

式中:r为曲线任一点半径,mm;t1为曲线长度比例,t1∈[0, 1];a为涡卷弹簧起始转角,取0;z为曲线距基准面位置,mm。
参照以下步骤[9-11]对模型进行分析,并对分析结构进行相应处理。将Creo生成的模型转存中性格式并导入ABAQUS中,提取中面,建立适于壳单元的模型,对内圈做一小段拆分(长度约25 mm)用于模拟内圈心轴;平面涡卷弹簧材料为钢,设定弹性模量2.06E5,泊松比0.3,赋予模型壳单元截面属性;建立频率提取分析步和静力通用分析步,设置输出变量包括Mises应力、RM(反作用力矩)、RF(反作用力)等;建立通用接触,接触属性为硬接触、无摩擦,并设立参考点,参考点与外圈建立MPC约束;建立边界条件,给内圈拆分部分施加固定约束,给参考点施加旋转位移6.28 rad(UR3);合理设置网格密度,采用S4R单元划分网格;建立分析用作业。有限元模型如图2所示。
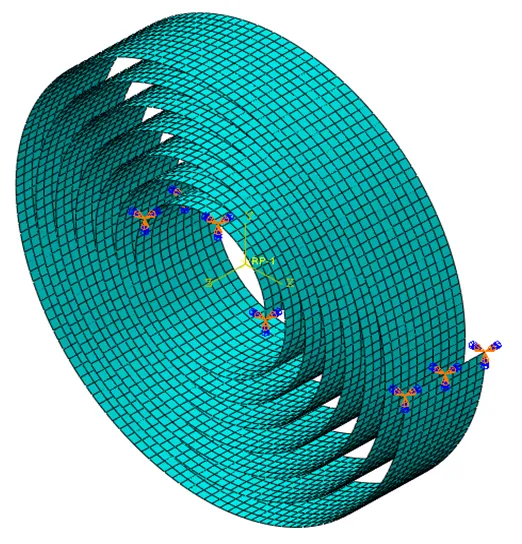
图2 ABAQUS有限元模型(n=7)
3 有限元分析结果
3.1 模态分析结果
在频率提取步中仅提取前30阶频率(表2仅列出前8阶频率)。通过分析得出,随着圈数的增大、节距的变小,平面涡卷弹簧的频率呈明显变大趋势,表中最小节距与最大节距基频相差近1倍。
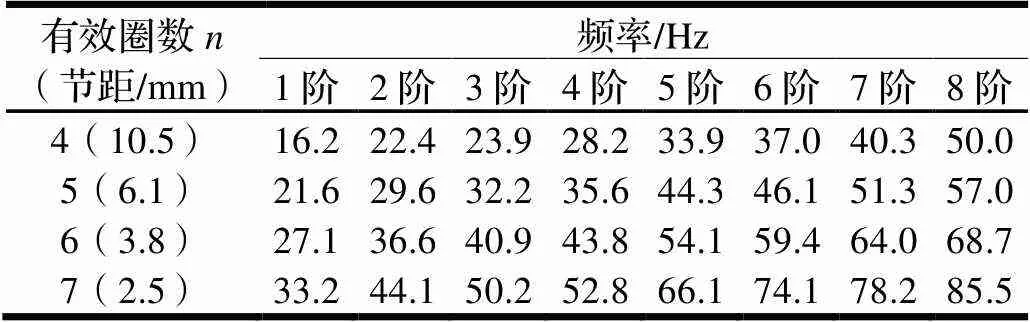
表2 有限元分析结果——频率
3.2 其他力学特性
在静力通用分析步中,平面涡卷弹簧的有限元分析结果如表3所示,Mises应力云图如图3所示。通过数据分析能够得出,最大应力(Mises)随着圈数的增大、节距的变小,呈小幅下降趋势,最大反作用扭矩(即扭转刚度)与最大反作用力基本相同。
3.3 应力沿变形后的分布曲线
应力沿平面涡卷弹簧长度方向的分布如图4所示,横坐标为参与变形长度,采用归一化处理,内圈参与变形初始位置为0、外圈末端为1。通过数据分析能够得出,随着圈数的增大、节距的变小,最大应力变小,沿长度方向应力波动幅度变小,且出现峰值的数量与有效圈数基本一致。通过对曲线数据进行处理发现,应力沿长度分布的均值基本相同。
4 仿真分析与经验公式计算对比
在相关弹簧手册或标准中,仅有关于扭转刚度、最大应力等参数的经验公式,没有模态、应力分布等相关的计算公式,因此仅对于扭转刚度、最大应力两个关注参数进行仿真分析与经验公式计算对比。
4.1 平面涡卷弹簧刚度对比
参照式(1)得到平面涡卷弹簧的经验公式刚度,并对ABAQUS分析结构最大反作用扭矩进行处理,得到仿真分析刚度如表4所示,仿真分析刚度和经验公式刚度存在一定的差别。

表3 有限元分析结果——应力、反作用力矩、反作用力、接触应力


图4 应力沿平面涡卷弹簧长度的分布

表4 仿真分析与经验公式对比——弹簧刚度
为了进一步分析仿真分析和经验公式计算结果的差别,基于7圈(=2.5 mm)的模型参数,加工了10个不锈钢材质的平面涡卷弹簧,并对刚度进行了测量,结果如表5,由于受测量精度、弹簧精度、摩擦影响等因素,导致被测弹簧个体之间的刚度存在一定的差异,但整体上试验测试刚度(均值)与仿真分析计算的刚度更为接近。
4.2 最大应力对比
参照式(3)计算弹簧在变形2π的最大应力并结合ABAQUS仿真分析结果,如表6所示。仿真分析最大应力和经验公式最大应力,计算还是存在一定的误差,主要是由于经验公式偏于保守(在应力校核时引入系数2,外圈转动时取2)。同时能够发现,仿真分析计算的平均应力与经验公式计算最大应力基本一致。

表5 平面涡卷弹簧刚度试验(n=7、t=2.5)

表6 仿真分析与经验公式对比——弹簧最大应力
5 结论
(1)从模态角度分析,随着圈数的增大、节距的变小,基频呈明显变大趋势;
(2)从应力角度分析,随着圈数的增大、节距的变小,最大工作应力呈小幅下降,应力沿长度方向的波动变小,分布更加均匀;
(3)仿真分析计算与经验公式计算对比发现,无论是刚度计算还是工作应力计算,都存在一定的差异。经验公式偏于保守,但经验公式更为简单、通用。有限元计算仿真过程及结果在平面涡卷弹簧的选用及设计中具有一定的参考意义,尤其是较高力学性能要求的平面涡卷弹簧。
(4)受限于ABAQUS软件收敛状况,本文的分析过程中没有引入摩擦,并且在分析过程中外圈施加位移仅为1圈,后续应进一步考虑引入摩擦的大转角工况。
[1]陶隆棋. 非接触平面涡卷与截锥螺旋弹簧优化设计[D]. 河北:燕山大学,2012.
[2]蔡宝,朱文华. 平面涡卷弹簧助力器设计及应用[J]. 上海第二工业大学学报,2017,34(3):203-208.
[3]沈波. 平面涡卷弹簧的应用[J]. 机械,2001,28(5):19-20.
[4]姜膺,张英会,万桂香,等. 平面涡卷弹簧设计计算[M]. 北京:机械工业出版社,1994.
[5]张英会,王德成. 弹簧手册[M]. 北京:机械工业出版社,2008.
[6]JB/T 5438-2008,平面涡卷弹簧设计标准[S]. 北京:机械工业出版社,1995:1-13.
[7]冯恒昌. 涡簧储能装置的设计及仿真研究[D]. 河北:华北电力大学,2012.
[8]孙京. 太阳翼铰链平面涡卷弹簧参数设计[J]. 航天器工程,2000(3):37-43.
[9]段巍,冯恒昌,王璋奇. 弹簧储能装置中平面涡卷弹簧的有限元分析[J]. 机械工程学报,2011,9(4):493-498.
[10]赵猛. 张力补偿装置用涡卷弹簧的研究分析[D]. 江苏:扬州大学,2013.
[11]赵孝谦. 平面涡卷弹簧性能分析与优化设计[D]. 辽宁:大连海事大学,2017.
Performance Analysis of non-Contact Planar Scroll Spring with the Same Stiffness Based on ABAQUS
RAN Jiangnan,DAI Guangyong,CAO Zizhen,YANG Tao,BAI Chunsheng
( Tianjin Institute of Astronautics Electromechanical Device, Tianjin 300458, China )
According to the empirical formula, the torsion stiffness of non-contact planar scroll spring is only related to its effective length under the same cross-section. In this paper, a set of mathematical models of non-contact planar scroll spring with the same stiffness are established, and the finite element modeling and analysis of each planar scroll spring is carried out based on the ABAQUS software. At the same time, the simulation results of the torsion stiffness and working stress of each spring are compared with the results of the empirical formula, and the test data are introduced into the comparison. The results show that with the same stiffness, the pitch becomes smaller, the fundamental frequency becomes larger, the maximum working stress decreases slightly, and stress fluctuation along the length direction becomes smaller and stress distribution becomes more uniform. There are some differences between the simulation results of torsional stiffness and maximum working stress and the results of empirical formula.
non-contact planar scroll spring;planar scroll spring;ABAQUS;finite element analysis
TH135+.1
A
10.3969/j.issn.1006-0316.2021.02.009
1006-0316 (2021) 02-0066-05
2020-05-25
冉江南(1985-),男,河北保定人,工程师,主要从事航天器结构和机构设计工作,E-mail:ranns@163.com。

