基于改进模拟退火-遗传算法的FMS生产排程优化分析
陈应飞,彭正超,胡晓兵,李彦儒
基于改进模拟退火-遗传算法的FMS生产排程优化分析
陈应飞1,彭正超1,胡晓兵1,李彦儒2
(1.四川大学 机械工程学院,四川 成都 610065;2.中国核动力研究设计院,四川 成都 610200)
制造型企业在采用柔性制造系统进行产品多品种生产加工时,车间生产调度问题(即生产排程)也是影响产品生产效率的一大重要因素。生产排程问题实际上是一个NP-C问题,它没有一个确定的解,只能是结果趋于最优,所以许多科研人员采用遗传算法来解决柔性制造系统的生产排程问题。本文以某机床厂的机床关键箱体类零件为研究对象,在遗传算法的基础上融入粒子群优化算法和模拟退火算法,对遗传算法的初始种群、交叉和变异操作等进行处理,期望能够使算法的收敛速度更快、结果更优。以该机床厂的需求为例,以成组布局的方式进行生产设备的布局,运用Matlab软件对其生产排程方案进行优化分析,结果表示针对该生产对象提出的生产排程优化算法有效可行,可以在实际生产中加以运用。
柔性制造系统;生产排程;模拟退火遗传算法;Matlab优化
现代制造型企业竞争越来越激烈,任何一个小的失误都可能导致整个市场的丢失,从而使得企业的经济受到较大的打击,甚至可能有破产的风险。在制造企业中,如何进一步提高零部件产品的生产效率始终是一个值得探索的问题。建立FMS(Flexible Manufacture System,柔性制造系统)是提高零部件产品生产效率的一项重要措施,但是如何在此基础上更进一步提高零部件产品的生产效率,经过研究人员大量的实验和分析研究发现,生产调度问题(又称生产排程)也是影响零部件产品生产效率的另一个重要因素。
为此,许多研究人员在生产排程问题上进行了大量的实验和数据分析,希望能得到最优的排程方式,使产品的生产效率能够提高到最大化。覃炳发等[1]对汽车零配件间的生产顺序进行研究并建出模型,在模型建立过程中对模型建立的关键点和困难点进行了汇总,对模型的最终实施效果进行了评定,最后建立了汽车零配件生产排程的线性整数规划模型;Gonzalo Mejía等[2]通过使用Petri网框架解决一般多目标调度问题,最后在大量的计算实验中验证了该通用框架在获得高质量解方便的适用性;潘怡颖等[3]研究了一种基于零件颜色和零件种类相融合的染色体编码方法,并且还构建了一种基于最大化零件生产量和最小化换色次数的多目标生产排程模型,通过使用遗传算法解决生产调度问题,最后通过实例验证了该方法的有效性和稳定性;李飞等[4]对生产排程优化中的遗传算法和模拟退火算法进行了详细介绍,并对两种优化算法进行了综合运用得到模拟退火遗传算法,对该算法的总体流程进行设计与改进,最后把该方法运用到分段车间实验中进行验证并与标准的遗传算法进行比较分析;钟志庆等[5]将绿色制造理念与零部件最短完工时间相结合,建立多目标生产排程优化问题,并通过遗传算法对该问题进行优化分析,最后通过合理设计出适应函数,选择、交叉和变异算子从而成功求解出模型。
1 机床关键箱体类零件生产计划问题
1.1 生产计划的概念和层次
生产计划是指企业对自身生产的产品形式和种类、产品数量、产品质量和生产进度进行统筹安排的过程。对于大型制造型企业来讲,生产计划可以分为两大类,一个是厂级生产计划,另一个是车间级生产计划。生产排程问题就属于车间级生产计划问题,其主要对产品加工过程中的工序进行合理安排。生产计划的具体层次和相应特征如表1所示。

表1 生产计划的层次和特征
1.2 生产计划约束条件
企业在制定生产计划的同时,也需要对产品的生产指标进行确定,如产品数量、产品质量等级、产值以及交货日期等。在完成指标的过程中,可能会受到某些方面的生产约束导致企业不能顺利完成生产指标。生产约束对企业生产所产生的效应类似于木桶效应,约束条件中的最低值将决定企业的最大生产能力。产生生产约束的原因是多方面的,有物料供应、企业生产能力、市场环境和资金等,其中物料供应、企业生产能力和市场环境是最主要的影响因素,其中企业生产能力是由企业自身条件决定的,企业可以通过不断的优化和改进提高自身的生产能力。
(1)企业生产能力,是指企业在一定的时间范围内,企业员工利用相关设备进行有效生产的产品的最大产量。企业生产能力的约束主要来自于生产设备、员工素质和生产流程等。
(2)物料供应,包括原材料、毛坯件、半成品件和成品件等。及时的物料供应能够最大程度地提高加工设备的利用率,从而能够提高产品产量、缩短生产周期。
(3)市场环境,也是影响企业生产计划的重要因素。决策者正确地判断市场发展趋势能够加大产品销售量,减少产品库存量,增加现金流,顺利开展下一项生产任务。
1.3 机床厂制定生产计划的基本流程
某机床厂在制定生产计划过程中的基本流程如图1所示。首先由营销部门根据销售订单类型和数量、单产品销售计划(非订单产品的销售计划)、企业自身的生产能力、生产成本和原料供应情况等制定月度销售计划,并下发至运行部。运行部门根据月度销售计划进行分解处理,制定出总生产计划,其中包括日生产计划、周生产计划和月生产计划,并下发至生产部。生产部门根据总生产计划要求进行产品的生产加工,产品加工完成后又返回营销部进行产品的销售。同时,生产部门也会根据生产车间的实际情况,实时地将生产情况反馈到营销部和运行部,确保能够及时地对销售计划和生产计划进行准确的调整,以免影响产品的生产和销售。

图1 某机床厂制定生产计划的基本流程
2 改良模拟退火遗传算法的设计
2.1 改良模拟退火遗传算法中的各种算法
(1)粒子群优化算法
粒子群优化算法,又称为微粒群优化算法,是科学家通过观察鸟类的觅食行为而逐步发展的一种随机搜索算法。粒子群算法进行优化计算的基本思路是将所求问题的解转换为三维空间中具有一定初速度和初始位置的微小粒子,并使这些微小粒子在解空间中不断地去寻找最优粒子,并且在寻找过程中粒子的速度和位置都会不断的调整。
粒子在解空间中的运动方程为:
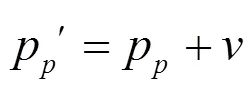
式中:为惯性权重;为粒子速度,为粒子下一个位置的速度;1、2为常数;1、2为随机数;b为当前个体的最佳位置;p为个体的当前位置;g为粒子种群的当前位置;p'为个体在p位置的后一个位置。
粒子群优化算法的基本流程如图2所示:①初始化粒子的相关参数,随机生成粒子的速度和位置信息;②通过目标函数计算粒子的适应度值;③通过公式更新各粒子和种群的速度与位置信息;④判断是否满足停止条件,如最大迭代数或是否收敛等,若满足停止条件则结束该算法,若不满足停止条件则返回第2步,依次循环。

图2 粒子群优化算法基本流程图
(2)模拟退火算法
模拟退火算法以其简便、灵活等特点在车间调度和组合优化问题中得到了比较广泛的使用。模拟退火算法最早由Metropolis等提出,其中心思想本质上就是不断迭代、不断改进的一个过程,并且有强的有限区域搜索能力。
模拟退火算法的数学公式为:

式中:P为新解取代旧解的概率;E表示目标函数的函数值为;E表示经过模拟退火算法迭代后的目标函数的函数值为;为算法中的温度控制参数。
可以看出,当参数的值较大时,旧解被新解取代的概率很高,但随着迭代的不断进行,参数的值越来越小、并最终趋近于0,此时旧解被取代的概率极低,并以此作为全局的最优解。
模拟退火算法的基本流程如图3所示:①设定初始状态值,确定温度参数,产生随机初始解E;②扰动产生新解E;③由Metropolis准则判断是否接受新的解,若接受新解则输出新解,若不接受新解则输出旧解;④判断由Metropolis准则输出的解是否满足停止条件,若满足则跳出计算、获得最优解,若不满足则改变控制参数的值、返回第2步,依次循环,直至获得最优解。
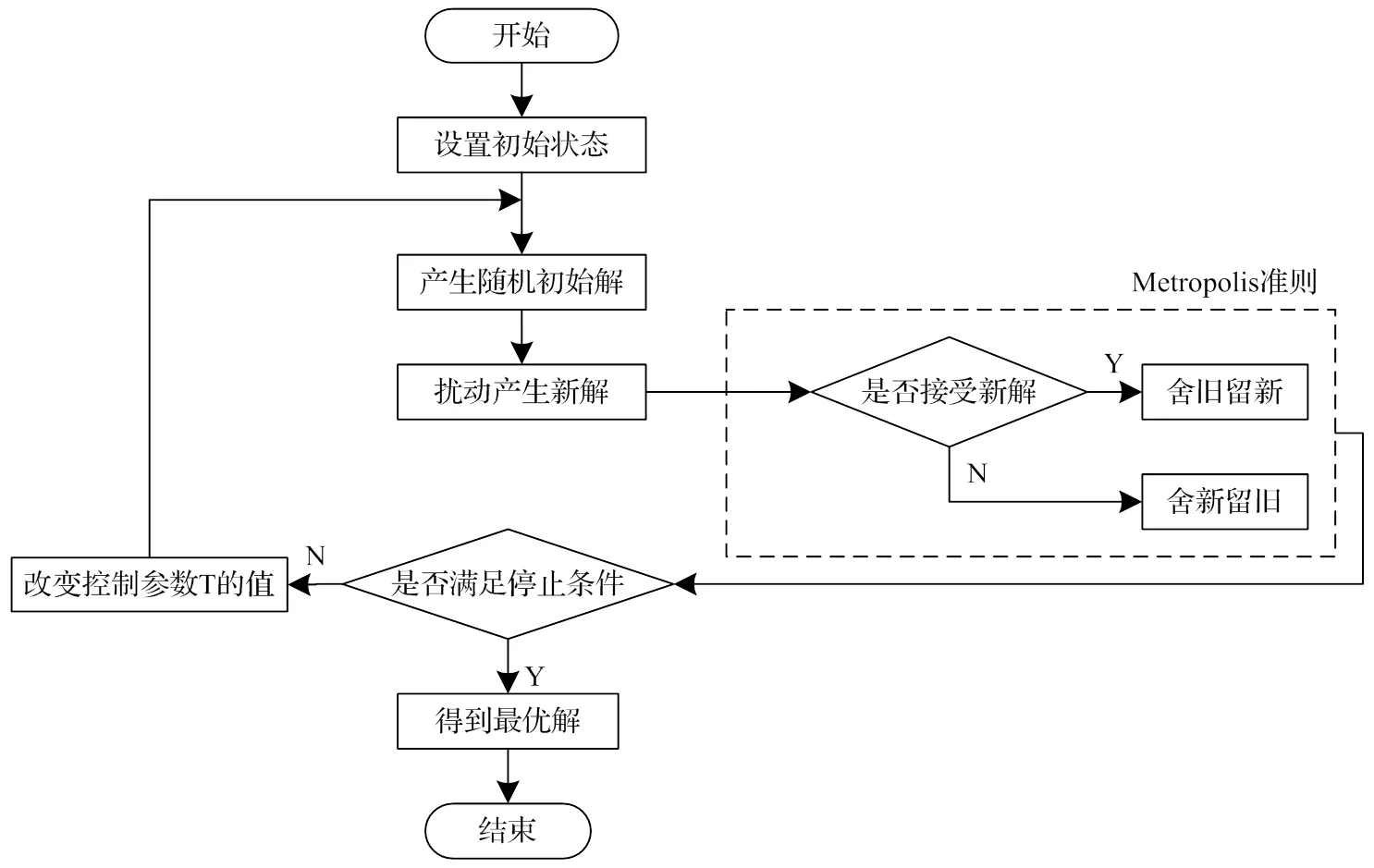
图3 模拟退火算法基本流程图
(3)遗传算法
遗传算法是一种借鉴生物界“优胜劣汰”机制演化过来的并行搜索方法[6],具有操作简单、通用性强、受约束条件少和全局搜索能力强等特点,在解决组合优化问题中得到了比较广泛的应用,也是未来智能制造领域的关键性技术之一。
运用遗传算法解决组合优化问题类似于求一个函数的最大值(或最小值)的优化问题,其数学规划模型为:

式中:max()为目标函数;为决策变量;∈、∈为约束条件;为基本空间;为的子集。
满足约束条件的解称作可行解,集合表示所有满足约束条件的解所组成的集合,称作可行解集合。
遗传算法基本流程如图4所示:①针对预解决问题的优化变量进行某种形式的编码;②确定问题的适应度函数并计算个体适应度值;③若满足优化精度或达到最大迭代次数则输出最有问题解,否则进入下一步;④选择、交叉、变异操作产生新个体,返回第二步,依次循环。
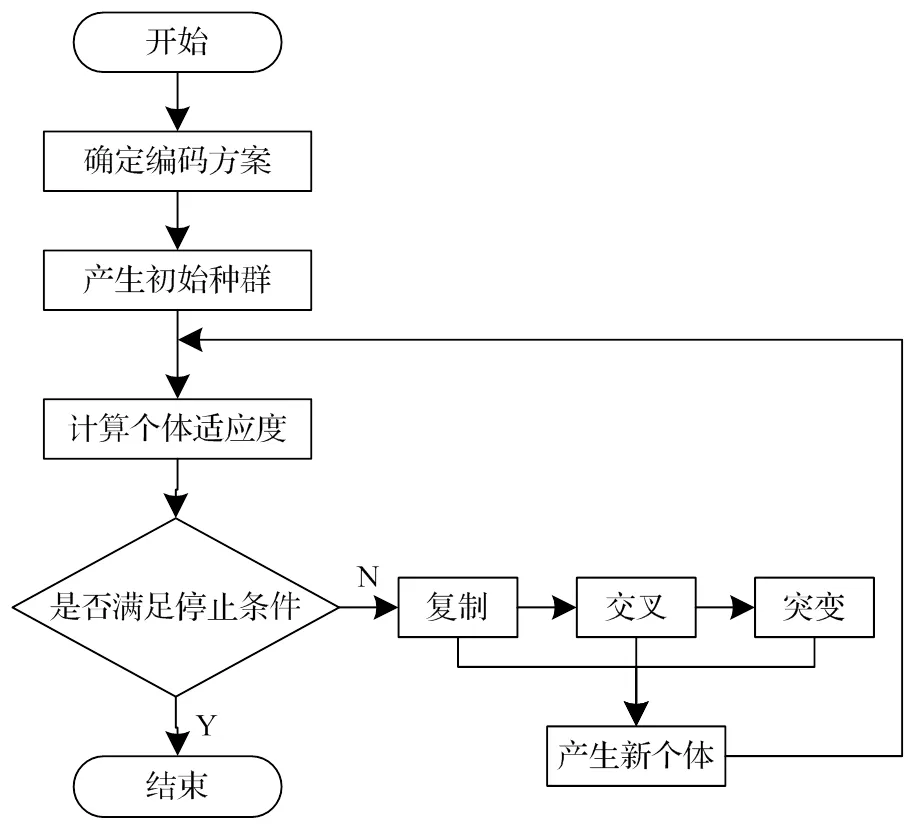
图4 遗传算法基本流程图
2.2 改良模拟退火遗传算法的设计
模拟退火算法几乎不具备全局空间搜索的能力,但其局部空间搜索能力较强,而遗传算法在局部寻优能力方面则较差,所以将模拟退火算法与遗传算法相结合,能够取长补短。再在遗传算法的种群初始化中融入粒子群优化算法,能够先一步优化种群个体,使得算法的优化效率更高,优化效果更好。改良模拟退火遗传算法流程图如图5所示。整个算法以遗传算法为主体,在初始化种群中融入粒子群优化算法,在交叉算子、变异算子和新个体适应度调整方面融入模拟退火算法。
改良模拟退火遗传算法基本流程如图5所示,具体步骤如下:
(1)设定算法相关固定参数,个体交叉概率P、个体变异概率P,模拟退火算法的初始温度0、种群规模、最大迭代数等;
(2)通过粒子群算法获得初始种群;
(3)评价种群中个体适应度,然后选择优秀个体生成种群,在选择优秀个体时采用轮盘赌法和最大保留法相结合的方式进行;
(4)进行个体交叉操作。以交叉概率为指标进行个体交叉,将产生的子代个体适应度值与父代个体适应度值进行比较,若子代个体适应度值大于父代个体适应度值则接受子代个体为当前个体;若子代个体适应度值小于或等于父代个体则按接受概率判断,若>random则接受子代个体为当前个体,否则保留父代个体为当前个体;
(5)进行个体变异操作。接受原则与个体交叉类似,以变异概率P作为判断指标;
(6)全局退火操作。全局退火观念即对全局范围内个体适应度值进行适当拉伸操作,避免个别特别优秀的个体充斥整个种群,影响搜索效率。在温度较高时使性能相似的个体在适应度值方面差异较小,在温度较低时扩大个体的适应度值,便于显示优秀个体的优势。

图5 改良模拟退火遗传算法基本流程图
其算法为:


式中:f为第个个体的适应度值,f'为第个个体迭代过后新的适应度值;为当前温度;为种群规模;为迭代次数;0为模拟退火算法中的初始温度。
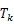
3 基于改良模拟退火遗传算法优化箱体类零件生产排程问题
3.1 约束条件
在应用FMS对机床箱体类零件进行生产加工时,以最大完工时间最小化作为优化目标,其数学模型为:
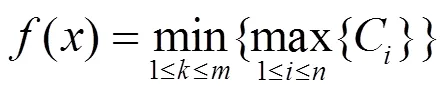
式中:为机器序号;为机器数量;为工件序号;为工件数量;C为工件完工时间。
还需要遵守如下规则:
(1)所有零件在初始时刻都可进行加工;
(2)零件的加工顺序没有具体要求,可随意变换;
(3)任何工序在同一时间都只能在一台设备上加工;
(4)一台设备在同一时间只能加工一个零件;
(5)每个零件都需具备合理的加工工艺;
(6)所有的零件都必须加工完成。
3.2 染色体编码
染色体编码是遗传算法的开端也是关键,优异的编码方式能够提高算法效率,避免陷入局部最优解。本案例属于柔性车间生产调度问题,其相对于一般的车间生产调度问题更加复杂。通过对类似案例的参考与分析,本案例采用双层编码方式进行染色体编码,第一层是基于机器的编码,依次按照工件工序所需加工机器的编号组成,第二层是基于工序的编码,由工件的工序号组成[7]。
比如,第一层机器编码为:
[1 2 1 5 7 2 5 2 1 2 1 7 1 2 6 2 1 7 1 2 6 1 2 7]
第二层工序编码为:
[1 2 4 4 3 1 2 1 3 4 1 2 4 3 1 2 3 1 4 3 4 1 1 3]
将第一层机器编码和第二层工序编码合并后得到染色体编码为:
[1 2 1 5 7 2 5 2 1 2 1 7 1 2 6 2 1 7 1 2 6 1 2 7 1 2 4 4 3 1 2 1 3 4 1 2 4 3 1 2 3 1 4 3 4 1 1 3]
3.3 适应度
适应度是评价个体适应环境能力的指标,适应度值越大则表示个体适应环境的能力越强,反之则表示个体适应环境的能力越弱。所以在进行子代生成时,应该尽量使适应度值大的个体作为父代,将父代优良基因遗传到子代。本实例以零件最大完工时间最小化作为优化目标,所以采用零件完工时间取倒数的方法作为适应度值的计算公式,即:

式中:F为适应度值;()为零件完工时间。
3.4 交叉与变异操作
在生物学中基因重组和变异是生物进化的原材料,在遗传算法中交叉和变异操作同样也是促进个体进化的原动力。在进行染色体基因交叉和变异操作时,由于本文把个体基因编码分为了机器编码和工序编码两层,所以针对不同的编码层采用不同的交叉和变异方式,以减少非法解出现的概率。
(1)交叉
在机器编码层采用等位基因随机交叉法,并结合模拟退火算法对新个体做出取舍判断。图6所示为机器编码层采用的等位基因随机交叉法的示例。交叉操作完成后,计算新个体1和2的适应度值,若适应度值大于旧个体(1、2)的适应度值则保留新个体,若适应度值小于旧个体的适应度值则以概率=exp(-Δ/T)进行判断新个体是保留还是舍弃。
在工序编码层则采用改进的POX交叉法,同样结合模拟退火算法对新个体进行取舍判断。图7所示为工序编码层采用的改进POX交叉法示例。交叉操作完成后,计算新个体1的适应度值,若适应度值大于交叉所用两个旧个体(1、2)的适应度值则保留新个体,若适应度值小于其中一个旧个体的适应度值则以概率=exp(-Δ/T)进行判断新个体是保留还是舍弃。
(2)变异
在机器编码层采用变异位随机分配可选机器法。在机器编码层中随机选择个变异位(一般变异位数不高于总位数的1/4),并在该位置随机分配可替换的机器序号,如图8所示。变异操作完成后,需要计算新个体1的适应度值,若适应度值大于旧个体(1)的适应度值则保留新个体,若适应度值小于旧个体的适应度值则以概率=exp(-Δ/T)进行判断新个体是保留还是舍弃。
在工序编码层采用末位随机插入法。将工序编码层中的最后一位随机的插入工序编码层中的某一位中,如图9所示。变异操作完成后,依然需要计算新个体1的适应度值,若适应度值大于旧个体(1)的适应度值则保留新个体,若适应度值小于旧个体的适应度值则以概率=exp(-Δ/T)进行判断新个体是保留还是舍弃。
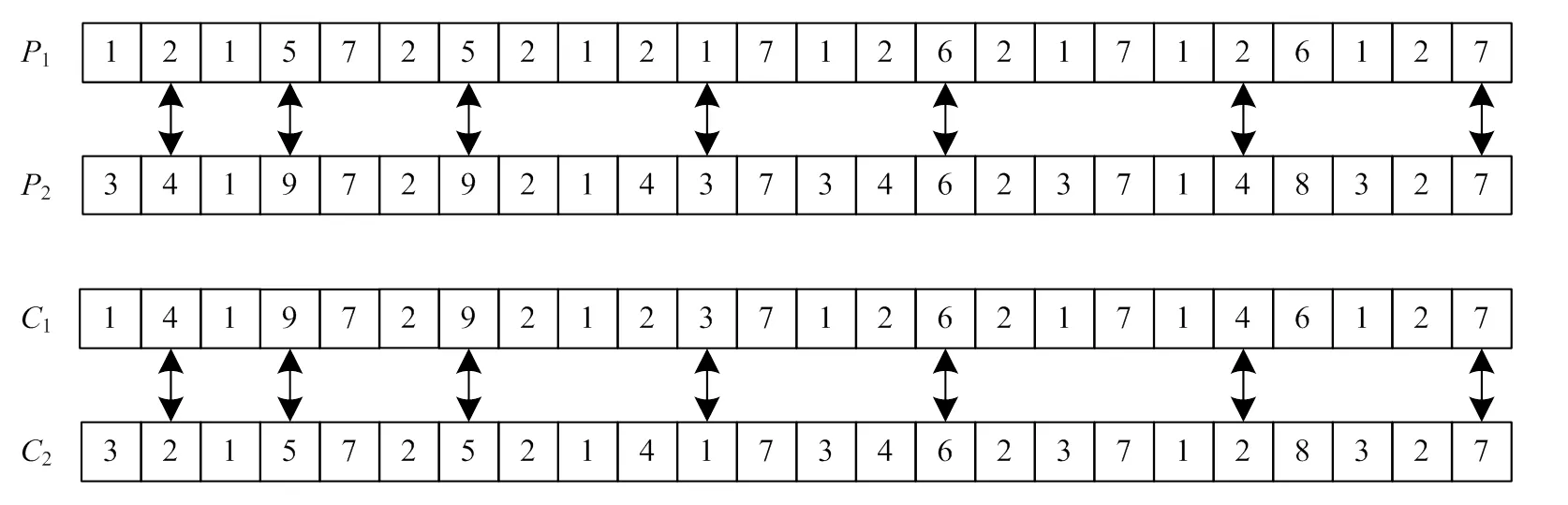
图6 机器编码层的等位基因随机交叉法示意图
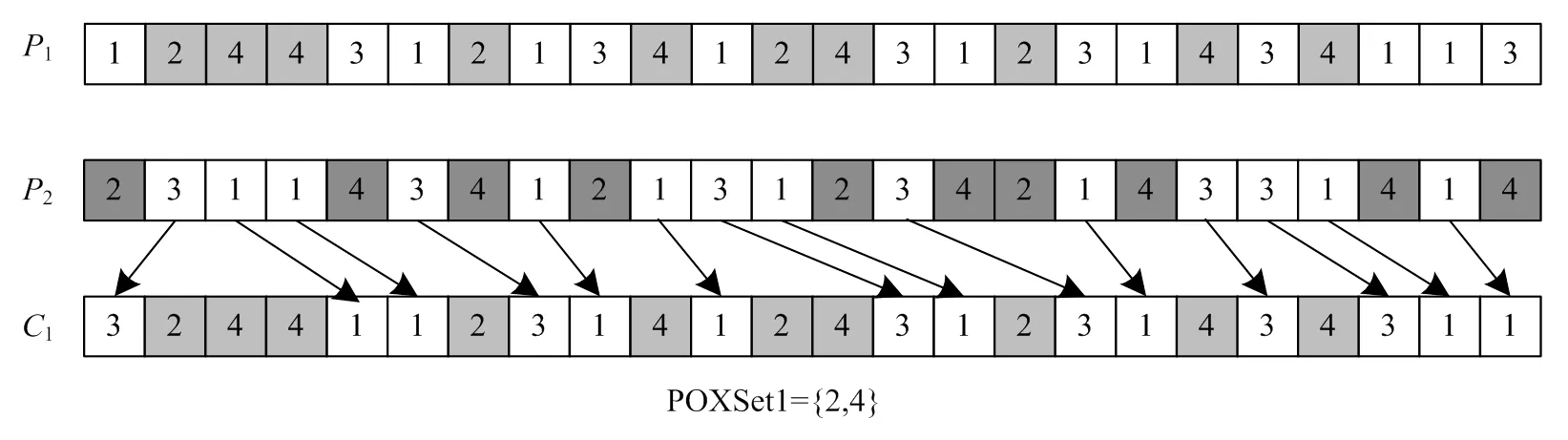
图7 工序编码层的改进POX交叉法示意图

图8 机器编码层的变异位随机分配法示意图
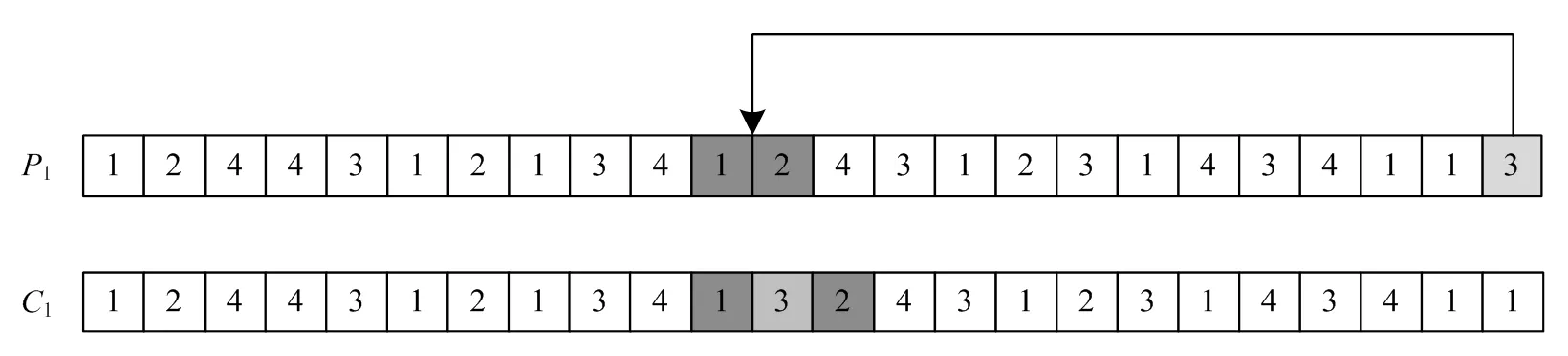
图9 工序编码层的末尾随机插入法示意图
4 机床箱体类零件生产排程实例仿真
改良模拟退火算法是在MATLAB R2019a平台上编程实现。计算机硬件和软件采用处理器Intel CORE i7第7代、主频2.80 GHz、内存8.0 GB、64位Windows10操作系统。该算法的固定参数设置为:种群大小=50,交叉概率P=0.8,变异概率P=0.03,最大迭代数=50,初始温度0=3000。
机床中4种典型箱体类零件在加工时所用设备的加工顺序及单机加工时间如表2所示。
表3为本实例中各个零件的各个工序的加工机器,如第一行第一列的[1 3]表示工件1的第1道工序可以在机器1或机器3上进行加工。
表4为本实例中各个零件的各个工序加工完成所需要的加工时间,如第一行第一列的36表示工件1的第1道工序所需加工时间为36 s。

表2 机床各箱体类零件机床安排时间表

表3 零件各工序所需的加工机器

表4 零件各工序所需的加工时间
经过MATLAB2019仿真后得到改良模拟退火遗传算法的进化曲线如图10所示。
传统模拟退火遗传算法优化后的染色体编码为[1 2 3 9 8 4 9 2 2 2 3 7 1 2 6 4 3 7 1 4 6 3 4 7 1 2 4 1 2 1 4 3 4 1 2 1 4 2 3 1 4 1 3 1 3 4 3 3],方案甘特图如图11所示,其最小化最大完工时间为648 s。
改良模拟退火遗传算法优化后的染色体编码为[3 2 1 5 8 2 5 2 3 2 3 8 1 2 6 2 1 7 3 2 6 3 2 7 3 1 2 1 4 2 3 1 3 2 4 1 4 3 2 4 3 1 4 3 1 4 1 1],方案甘特图如图12所示,其最小化最大完工时间为592 s,加工效率比传统模拟退火遗传算法提高了约11%。

图10 改良模拟退火遗传算法进化曲线图

图11 传统模拟退火遗传算法方案甘特图

图12 改良模拟退火遗传算法方案甘特图
5 小结
本文对柔性车间生产排程的相关概念和评价方法等做了简要总结,同时结合课题项目对某机床厂机床关键箱体零件的生产计划问题进行了简单的分析,并且运用改良后的模拟退火遗传算法对本项目中柔性车间的生产排程问题进行了优化分析,优化结果显示:以最小化最大完工时间为目标、运用改良算法优化后的排程计划时间比原计划时间节省了约11%。经过科研人员的不断创新和改进,如今生产排程优化的方法有很多,但无论是采用哪一种方式方法,其最终目的都是使企业能够达到经济效益最大化,那么对于生产排程结果的评价就显得十分重要。目前,对生产排程结果的评价基准主要有完工时间最短、设备利用率最大、工件半成品数量最小和交货时间最短等方面,大多数的优化算法也是根据以上几方面为目标进行优化改进的。
改良模拟退火遗传算法依托于遗传算法、模拟退火算法和粒子群优化算法,区别于传统的模拟退火遗传算法,在初始种群中融入粒子群优化算法加强了初始种群的筛选,在遗传算法的交叉、变异操作融入了模拟退火算法加强了局部搜索能力,再在得到的新个体中融入全局退火操作,对新个体的适应度值进行拉伸,有助于扩大个体间的适应度差异,便于寻优。关于车间调度排程问题的研究发展至今,将生产排程计划与人工智能、专家系统等相结合是未来研究的主要方向,更加能够解决各种复杂的生产排程问题,提升企业的生产效率。
[1]覃炳发,蒋缘,潘玉雯. 汽配件制造业钟的生产排程模型研究[J].计算机产品与流通,2019(10):266.
[2]Gonzalo Mejia,Jordi Pereira. Multiobjective scheduling algorithm for flexible manufacturing systems with Petri nets[J]. Journal of Manufacturing Systems,2020(54):272-284.
[3]潘怡颖,徐嘉杰. 基于遗传算法的汽车零配件生产排程问题[J]. 海峡科技与产业,2019(3):116-122.
[4]李飞. 船体车间的分段生产排程优化研究[D]. 镇江:江苏科技大学,2019.
[5]钟志庆. 面向FMS的低碳生产排程方法研究[J]. 制造技术与机床,2019,1(7):23-27.
[6]杨智超,邓斌. 基于遗传算法对液压阀用磁流变液阻尼器的优化设计[J]. 机械,2019,46(11):52-57.
[7]张炳根,龙伟. 基于遗传算法的制造单元继承性生成方法[J].机械,2018,45(1):18-23.
[8]宗玉杰,崔建伟. 模拟退火遗传算法在机械臂路径规划中的应用[J]. 测控技术,2018,37(3):1-5.
[9]韩文民,范吉文. 基于改进遗传算法的柔性作业车间调度问题研究[J]. 科学技术与工程,2008,8(22):6135-6137.
[10]邓炎泽. 关于典型箱体类零件加工工艺的思考与探讨[J]. 科技与创新,2016(21):25-25.
[11]Leilei Meng,Chaoyong Zhang,Yaping Ren,et al. Mixed-integer linear programming and constraint programming formulations for solving distributed flexible job shop scheduling problem[J]. Computers & Industrial Engineering,2020(142):45-52.
[12]吴树景,游有鹏,罗福源. 变邻域保优遗传算法求解柔性车间调度问题[J]. 计算机工程与应用,2010,4(5):242-249.
Analysis of FMS Scheduling Optimization Based on Improved Simulated Genetic Annealing Algorithm
CHEN Yingfei1,PENG Zhengchao1,HU Xiaobing1,LI Yanru2
(1.School of Mechanical Engineering, Sichuan University,Chengdu 610065, China; 2.Nuclear Power Institute of China, Chengdu 610200, China)
Job scheduling problem (production scheduling) is an important factor affecting the production efficiency when using FMS in production and processing. Production scheduling is actually a problem of NP-C. There is no definite solution for the problem, but the results can be optimized. Many researchers use genetic algorithm to solve FJSP. This paper studies the key box parts of machine tools in a machine tool factory. We incorporate GA with PSO and SA to deal with the initial population, crossover and mutation operations of GA, hoping to make the algorithm converge faster and get better results. The equipment was laid out in groups. The production scheduling scheme was optimized and analyzed by MATLAB. The results show that the production scheduling optimization algorithm proposed for this factory is effective and feasible. It can be applied in actual production.
flexible manufacturing system;production scheduling;improved simulated annealing genetic algorithm;Matlab optimization
TH164;TP315
A
10.3969/j.issn.1006-0316.2021.02.002
1006-0316 (2021) 02-0007-10
2020-06-01
国家科技重大专项(2018ZX04032001)
陈应飞(1994-),男,四川成都人,硕士研究生,主要研究方向为智能制造、数字化生产,E-mail:1564647444@qq.com;胡晓兵(1970-),男,湖北武汉人,博士,教授,主要研究方向为企业信息化、机器视觉、数字化车间,E-mail:huxb@ scu.edu.cn。

