基于Romax的功率分流齿轮箱齿轮修形仿真分析

周杜，郑传统

基于Romax的功率分流齿轮箱齿轮修形仿真分析

周杜，郑传统

（明阳智慧能源集团股份公司 风能研究院，广东 中山 528437）

齿轮箱的可靠性和寿命对风力发电机组的平稳运行起着至关重要的作用，齿轮修形能有效地减小齿轮箱振动、降低噪音以及延长使用寿命。本文以5 MW功率分流风电齿轮箱为研究对象，简要介绍了齿轮修形理论以及功率分流式风电齿轮箱的基本结构；利用Romax软件建立了5 MW功率分流齿轮箱模型，利用载荷谱对齿轮箱进行静力学仿真分析，根据齿轮载荷分布、传动误差等参数，对一、二级的齿轮进行齿廓和齿向修形，实现功率分流式风电齿轮箱齿轮间的均载特性，减小齿轮传动误差。

功率分流；风电齿轮箱；齿轮修形；Romax；均载

风电市场去补贴的时代即将到来，国内风电行业竞争日益激烈，新兴机型逐渐向大兆瓦、轻量化、高可靠性、低成本的方向发展。风电齿轮箱[1]作为风力发电机关键部件之一，因为多变的工况载荷及制造安装误差等因素，使得齿轮不可避免地产生冲击、振动和偏载，从而导致齿轮在早期失效概率增加。如何提高齿轮箱的均载特性、延长寿命成为风电行业关注的热点问题。对齿轮进行修形，能有效减少轮齿受载变形和制造误差引起的啮合冲击，获得较为均匀的载荷分布，提高齿轮的的啮合性能和承载能力。国内外许多专家学者[2-4]对齿轮修形进行了大量研究，范孝良等[5]利用Romax建立了2 MW齿轮箱模型，采用齿向和齿阔修形方法有效地降低传动误差，提高了齿轮的承载能力；王彬等[6]以中低速齿轮箱为研究对象，通过Romax进行仿真分析和优化，对比了齿轮修形前后载荷分布情况，得出了合理修形能够改善齿面载荷分布和减小传递误差的结论；方振江[7]利用Romax建立功率分流齿轮箱模型，并对此进行分析优化，极大地减少了设计失误。由此可见，深入研究齿轮修形[8-9]技术对风电齿轮箱具有重要意义。

1 齿轮修形理论

图1为一对齿轮的啮合过程，随着齿轮的旋转，齿轮啮合线进入啮合，由于齿轮副均为弹性体，在力的作用下齿轮将会发生弹性变形，使主、被动齿轮的基节不再相等。如图1（a）所示，当齿对2进入啮入位置时，由于齿对1的变形，主动轮基节P1＜被动基节P2，导致齿轮啮入点啮合力增加，形成啮入冲击。相同地，如图1（b）所示，在齿对1即将脱离啮合接触时，由于齿对2的变形，P1＞P2，主动轮齿顶将沿着被动轮齿根刮行，形成啮出冲击。

齿轮装置在功率传递时，由于受到载荷的作用，各个零部件都会产生不同程度的弹性变形，包括轮齿、轮体、箱体、轴承等的变形。尤其是与齿轮相关的弹性变形，如轮齿变形和轮体变形，会引起齿轮的齿廓和齿向的畸变，使齿轮在啮合过程中产生冲击、振动和偏载。为了消除轮齿啮入和啮出冲击，通常采用齿廓修形的方法，即沿着齿高方向从齿面上去除一部分材料，从而改变齿廓形状，消除齿对在啮入、啮出位置的几何干涉。而齿向修形是根据轮齿受力后产生的变形，将齿轮螺旋角和轴向齿形按预定规律进行修正，以获得较为均匀的齿向载荷分布。

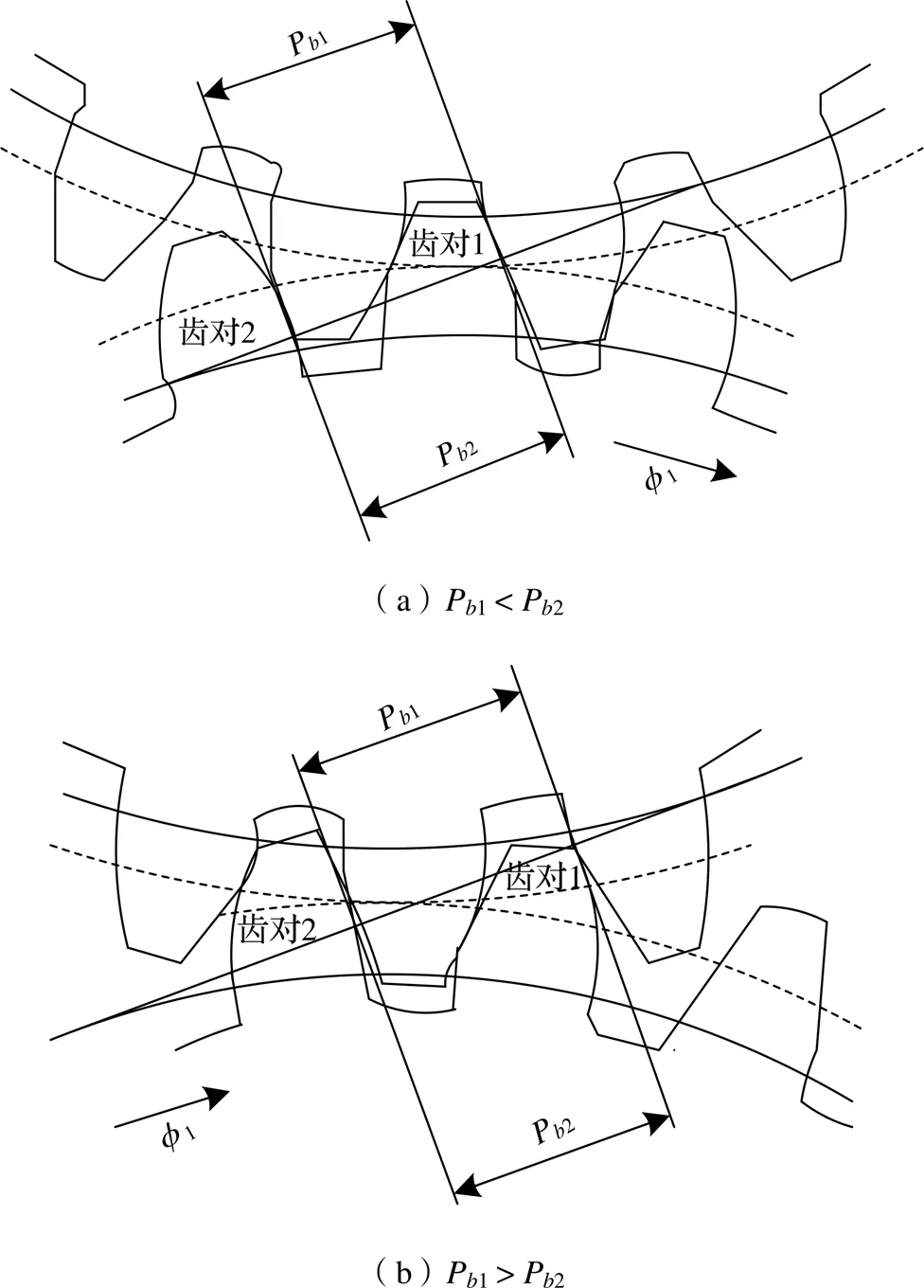
图1 一对齿轮的啮合过程示意图

2 功率分流风电齿轮箱基本结构及传动原理

图2为某5 MW功率分流风电齿轮箱[10]传动系统的结构简图，表1为齿轮箱基本参数表。该系统由两级行星齿轮传动构成，输入轴同时与第一级内齿圈和第二级行星架固定连接，第一级行星架固定，第一级的太阳轮与第二级的内齿圈固定连接且浮动，第二级太阳轮作为输出轴。输入力矩一部分由第一级的内齿圈承担，另一部分由第二级的行星架承担，因而被称为功率分流，最后在第二级太阳轮实现汇流。这种结构的齿轮箱空间布局紧凑，大大减少了齿轮箱尺寸，从而节省了制造成本。

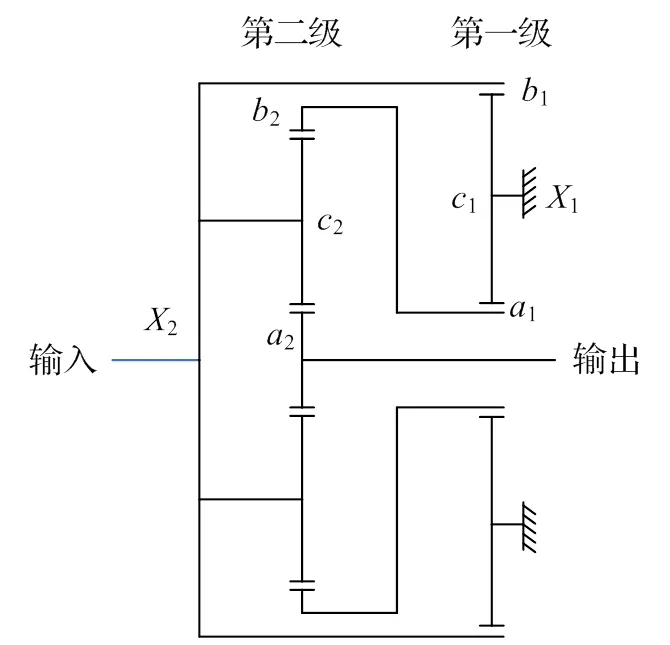
图2 功率分流齿轮箱结构简图

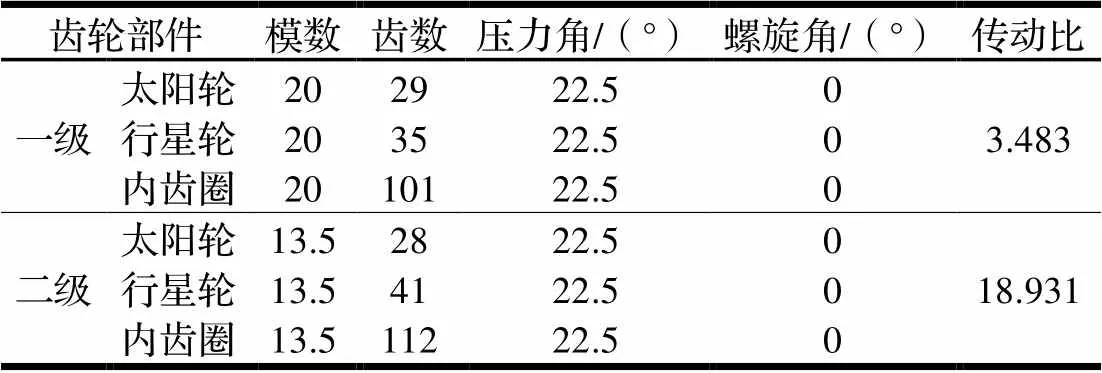
表1 齿轮参数

令第一级行星的太阳轮、行星轮和内齿圈齿数分别为1、2、3，转速分别为1、2、3，第二级行星的太阳轮、行星轮和内齿圈齿数分别为1、2、3，转速分别为1、2、3。

第一级行星架固定，等价于定轴轮系，则第一级太阳轮的转速为：

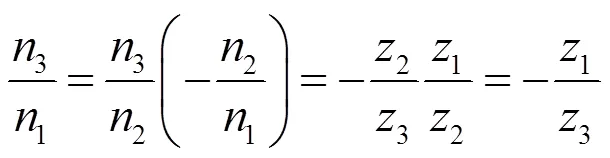
所以有：

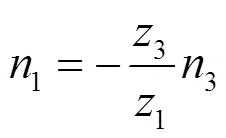
第二级内齿圈与第一级太阳轮的转速相同，即：

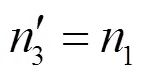
对于第二级，全局附加逆时针转速n'，则第二级行星架的转速为零，等价于定轴轮系，则第二级太阳轮的转速为：

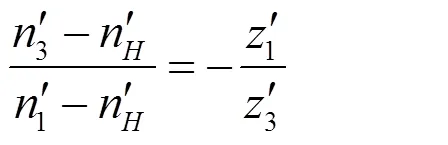
所以：

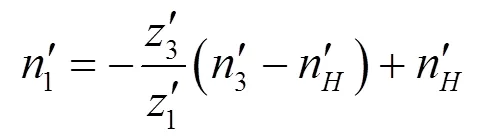
又有：

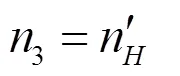
将式（1）、（2）和（4）代入式（3）得：

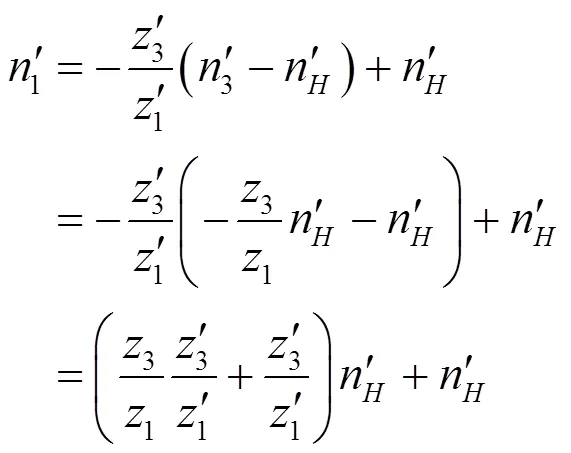
则差动行星的传动比为：

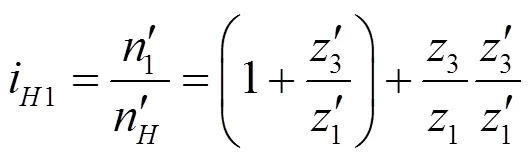
第一级齿圈输入功率占总功率百分比为：

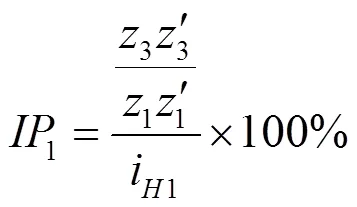
将齿轮参数代入式（9），可得第一级行星功率分流比重为73.5883%，第二级行星功率分流比重为26.4117%。

3 Romax系统建模

根据5 MW功率分流齿轮箱的结构尺寸参数，在Romax中建立齿轮箱传动链，为了使仿真结果与齿轮箱实际运行工况更加吻合，将考虑轮毂、发电机等零部件对齿轮箱的影响。建模分成两部分：一是运用三维参数化建模，对于轴、齿轮、轴承等可视作刚体的零部件，在Romax中直接建模，并定义材料属性；二是对于轮毂、行星架、箱体、发电机外壳等柔体类零部件的建模，通过有限元软件进行网格划分，并定义材料属性，并在Romax中定义Stiffness Component组件，将有限元模型导入其中，获得节点形式的柔性体三维模型，最后再通过缩聚节点与其他刚体零件连接在一起。图3所示为5 MW功率分流齿轮箱传动系统模型。

图3 5 MW功率分流齿轮箱传动系统模型

4 齿轮修形仿真分析

4.1 齿廓修形

齿廓修形采用渐开线曲线长修形，适用于风电齿轮箱中的大载荷，其中行星轮按照与内齿圈啮合点选取修形起始点。齿廓最大修形量由齿轮受载产生的变形量决定，采用石川公式法[11]确定最大修形量。图4为改进石川法近似齿形，图5为齿轮简化图。

根据石川公式，将齿轮看做一个由梯形和长方形组成的悬臂梁。

齿轮在载荷作用点沿啮合线方向的变形量可以表示为：

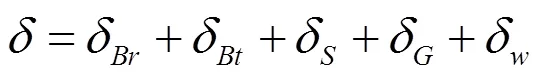
式中：δBr为长方形部分的弯曲变形量，mm；δBt为梯形部分的变形量，mm；δS为由剪力产生的变形量，mm；δG为基础部分倾斜产生的变形量，mm；δw为腹板产生的变形量，mm。

r.分度圆半径rb.基圆半径hDi.腹板半径

长方形部分的弯曲变形量如式（11）所示，梯形部分的变形量如式（12）所示，剪力产生的变形量如式（13）所示，基础部分产生的变形量如式（14）所示，切向力和弯矩对腹板产生的变形如式（15）所示。

式中：F为啮合点受力，N；α为齿轮啮合角，rad；为弹性模量，MPa；为齿厚，mm；为泊松比。

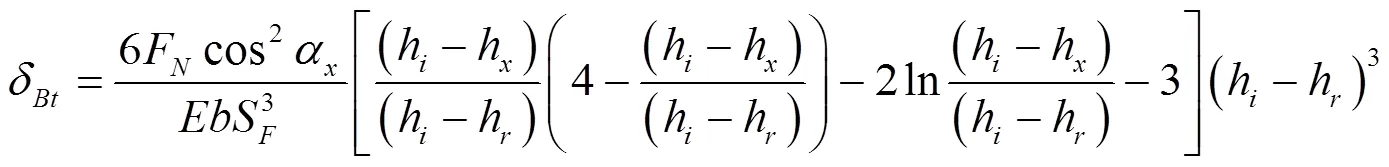
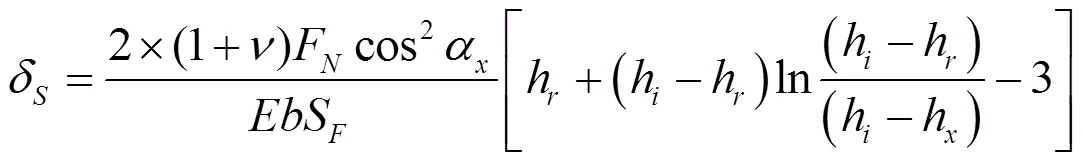
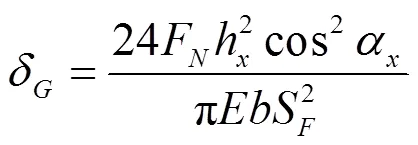
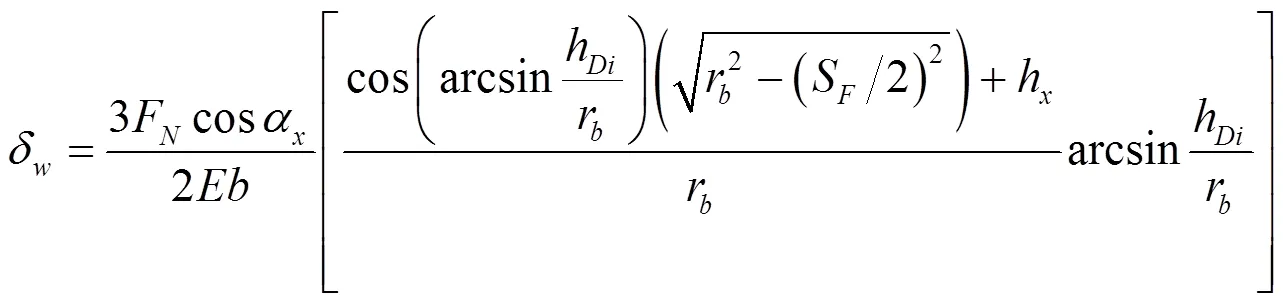
最大修形量为：

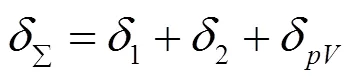
式中：1、2为对应于各个齿轮的变形值，mm；δ为齿轮接触部分的变形量，mm。

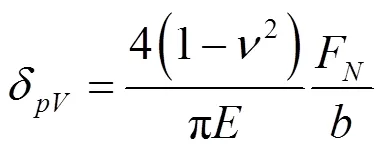
4.2 齿向修形

4.2.1 鼓形修形

齿轮传动系统在载荷的作用下会产生弹性变形，包括轮齿的弯曲变形、剪切变形和接触变形，还有支撑轴的弯曲变形和扭转变形，这些变形将会使轮齿的螺旋线发生畸变，导致轮齿沿一端接触，造成载荷分布不均匀，出现偏载现象。

设计鼓形修形的最主要的、目的是保证在最大啮合歪斜度条件下互相啮合的齿轮不发生端点接触——相切而不相割，减少棱边效应；同时还应保证在不倾斜或少量倾斜情况下，最大限度地减少单位齿长上的载荷。图6为鼓形齿结构图。

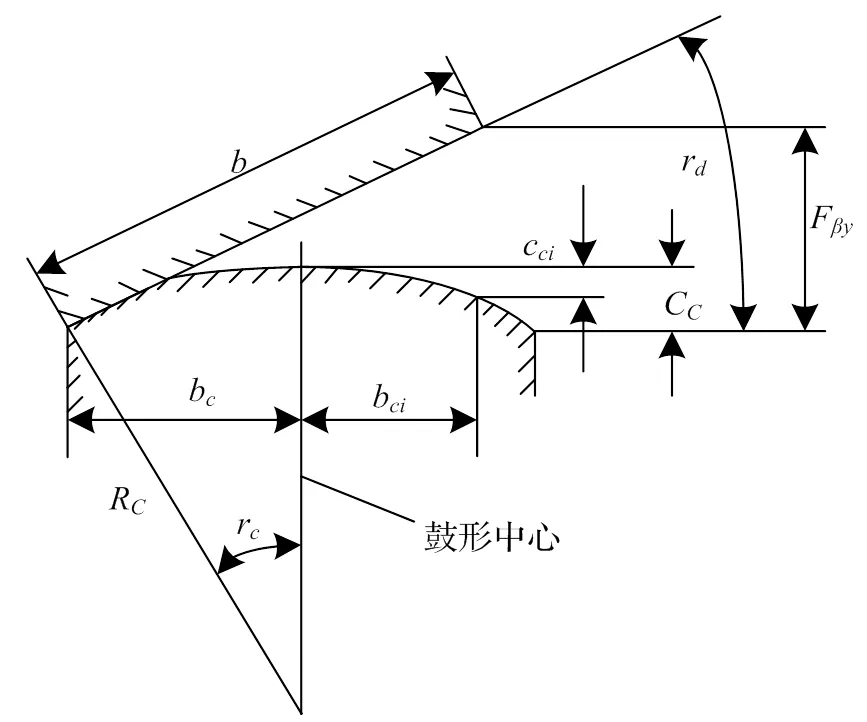
图6 鼓形齿结构

本文对鼓形量的求解仅考虑啮合歪斜度，并未考虑轮齿的变形因素。

只考虑歪斜度所需要的鼓形量为：

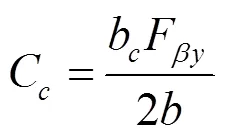
当鼓形中心在齿宽的中间，则有：

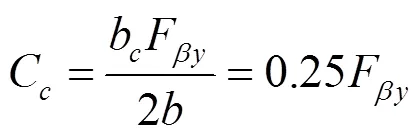
影响啮合歪斜度F的主要因素有空间几何因素、机件刚度因素及工作条件因素。本中采用ISO计算方法求解啮合歪斜度，即：

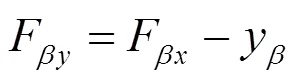
初始啮合齿向误差F按三种情况求解：

（1）在载荷作用下没达到全齿宽接触或未能验证有良好的接触，有：

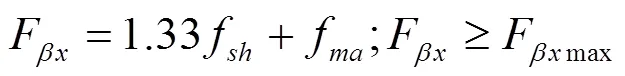
（2）当已正是达到所希望的接触斑点，有：

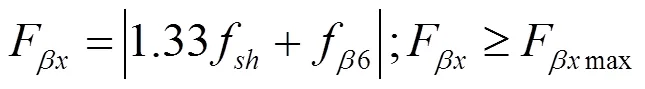
（3）在载荷作用下达到理想接触斑点，有：

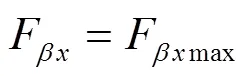
式中：Fmax为最小啮合齿向误差，mm；f为综合变形产生的啮合齿向误差分量，mm；f为制造安装误差产生的啮合齿向误差分量，mm；f6为GB 10095－88的6级精度的齿向公差，mm；y为齿向跑合量，mm。

4.2.2 螺旋角修形

当齿轮的精度和传动结构形式确定，则啮合歪斜度F也就确定下来，因此引入螺旋角修形，即在一对啮合齿轮副中的一个齿轮齿向方向有一个偏斜量，以弥补部分歪斜度。带鼓形量的螺旋角修形，不仅可以保证相切而不相割的条件，同时又能最大限度提高齿轮承载能力。

对于太阳轮的扭转变形，假设齿宽方向上载荷均匀分布，则最大相对扭转角为：

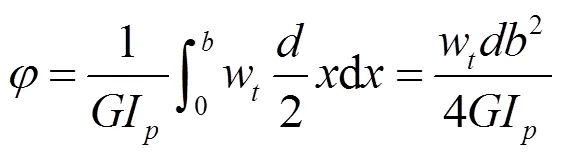
式中：为扭转角，rad；为剪切弹性模量，MPa，齿轮钢一般取＝7.95×104MPa；I为极惯性矩，mm4，I＝π4/32K；为分度圆直径，mm；K为考虑齿轮内孔影响的系数，K＝[1－(d/)]-1；d为内孔直径，mm；w为单位齿宽载荷，N/mm，w＝F/；F为总切向力，N；为齿宽，mm；为齿宽方向上坐标，mm。

则齿宽范围内的最大相对扭转变形为：

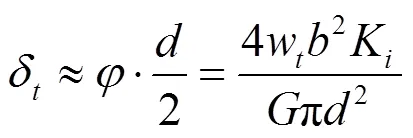
式中：δ为扭转变形，mm。

令宽径比Ψ＝/，则有：

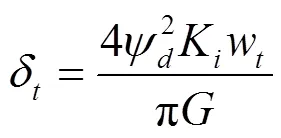
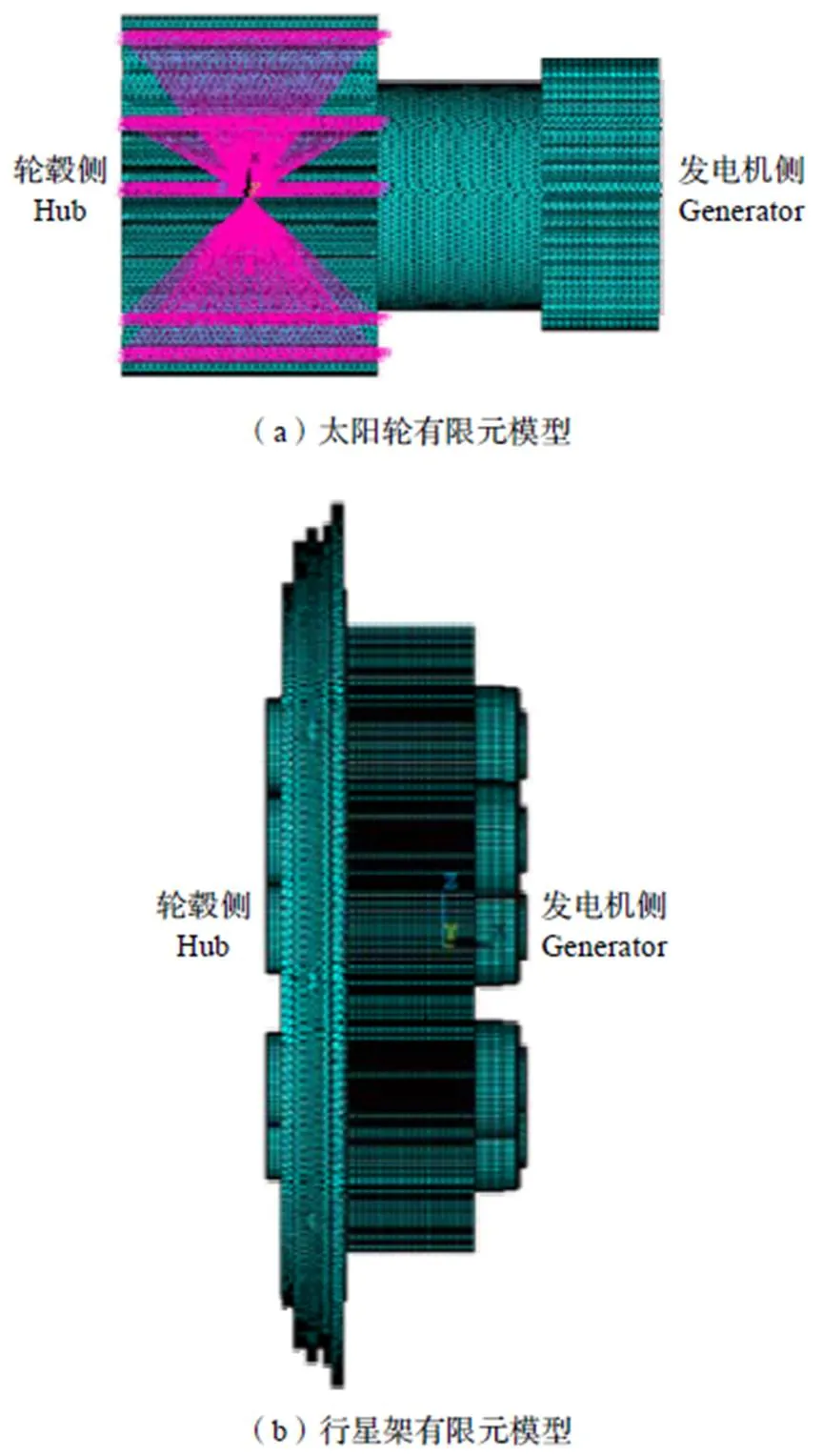
通过有限元计算同样可以得到轴和行星架的扭转变形。图7是太阳轮、行星架、行星轮有限元模型。

行星轮采用柔性销结构支撑，按理只需进行鼓形修形，但根据行星系统刚度在啮合线方向反映的变形量可进行适当的螺旋角修形，修形量的大小根据行星轮在内啮合处齿向的相对变形量，修形方向为右旋修形。齿廓修形同修形原则一致。

太阳轮螺旋线修形量同时考虑三个因素的叠加，①行星轮修形（右旋），②行星架的变形引起外啮合处的变形（左偏），③太阳轮的扭转变形，对于双齿浮动（右偏）对应太阳轮上的螺旋线修形量为1＝1左旋＋2右旋＋3左旋，鼓形修形量考虑啮合歪斜度的影响。齿廓修形同修形原则一致。

内齿圈考虑到加工工艺等问题，一般不进行修形。

通过以上方法对一、二级的太阳轮、行星轮、内齿圈进行齿廓和齿向修形，在工程计算和有限元计算的结果上进行微调，得到齿轮修形参数如表2所示。

该模型仅考虑了扭矩，不考虑重力和弯矩的影响，齿轮箱额定输入功率5620 kW，额定输入转速10.5 r/min，额定扭矩5111.5 kN·m。分别对齿轮箱修形前后进行Romax仿真分析。

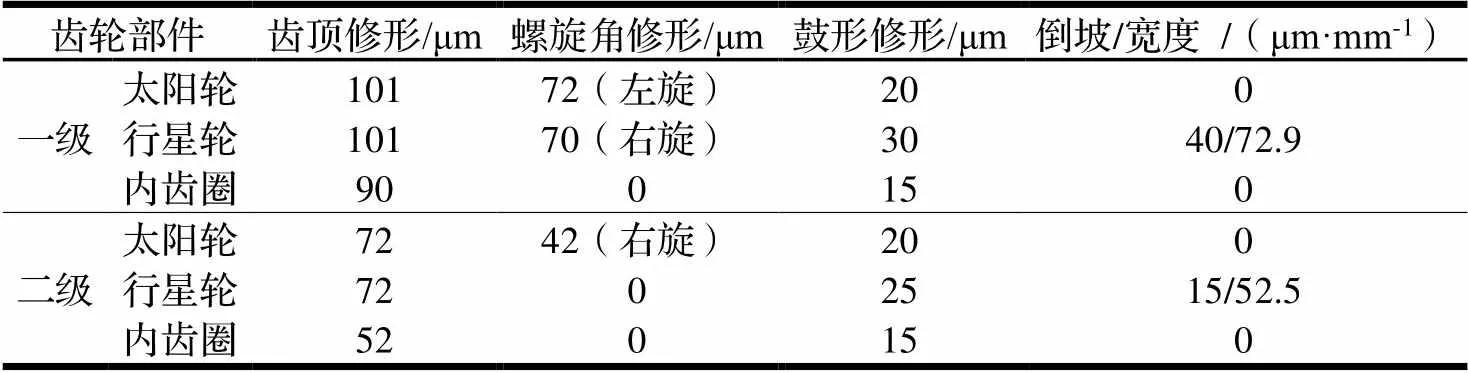
表2 齿轮修形参数

4.3 接触斑

对比一、二级行星内外啮合齿轮的接触斑。图8、图9是修形前、后一级内齿圈和太阳轮上的接触斑。图10、图11是修形前、后二级级内齿圈和太阳轮上的接触斑。

通过对比修形前后齿轮的接触斑，可以发现齿轮修形可以有效解决齿轮啮合过程中的偏载问题。修形前，沿齿宽方向承受载荷的宽度约占整个宽度的1/2，且载荷分布极不均匀。修形后，在齿宽方向上，载荷由中间向两边递减，呈对称分布，齿面受载更加均匀，且齿宽方向参与承载的宽度变大了，整个齿宽方向上几乎都有载荷分布，增加了齿轮的承载能力。

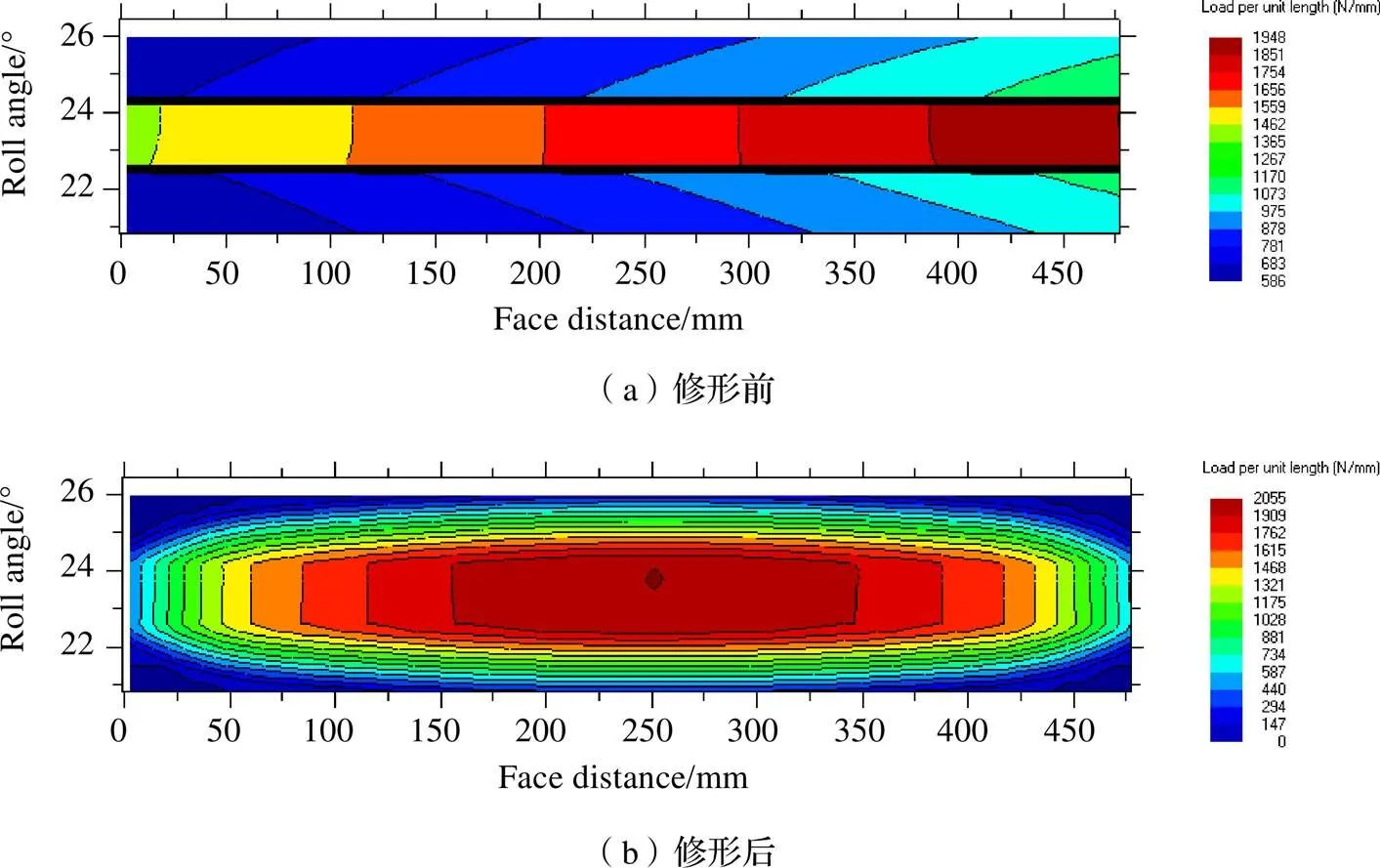
图8 一级内啮合修形前后接触斑

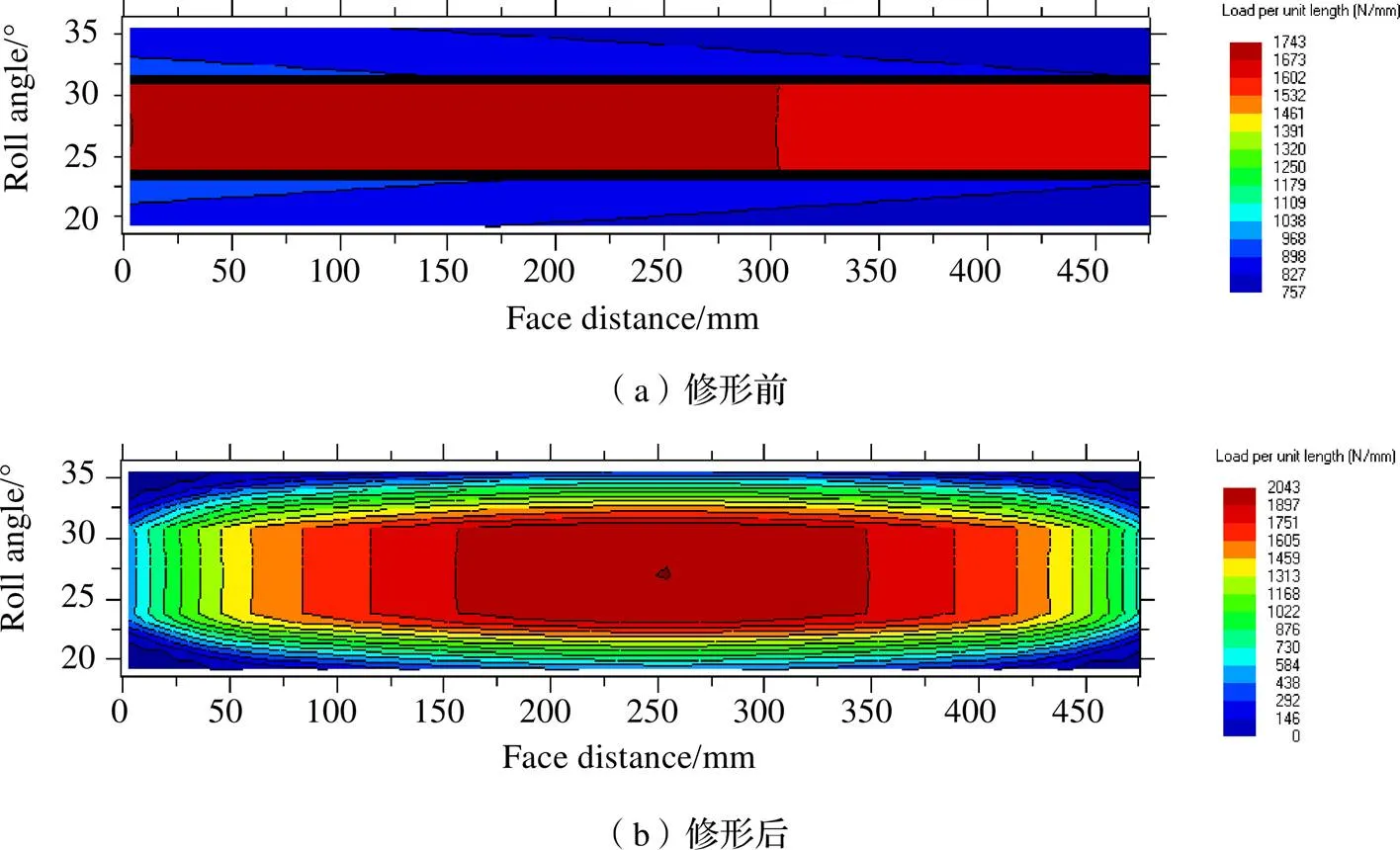
图9 一级外啮合修形前后接触斑

图10 二级内啮合修形后接触斑

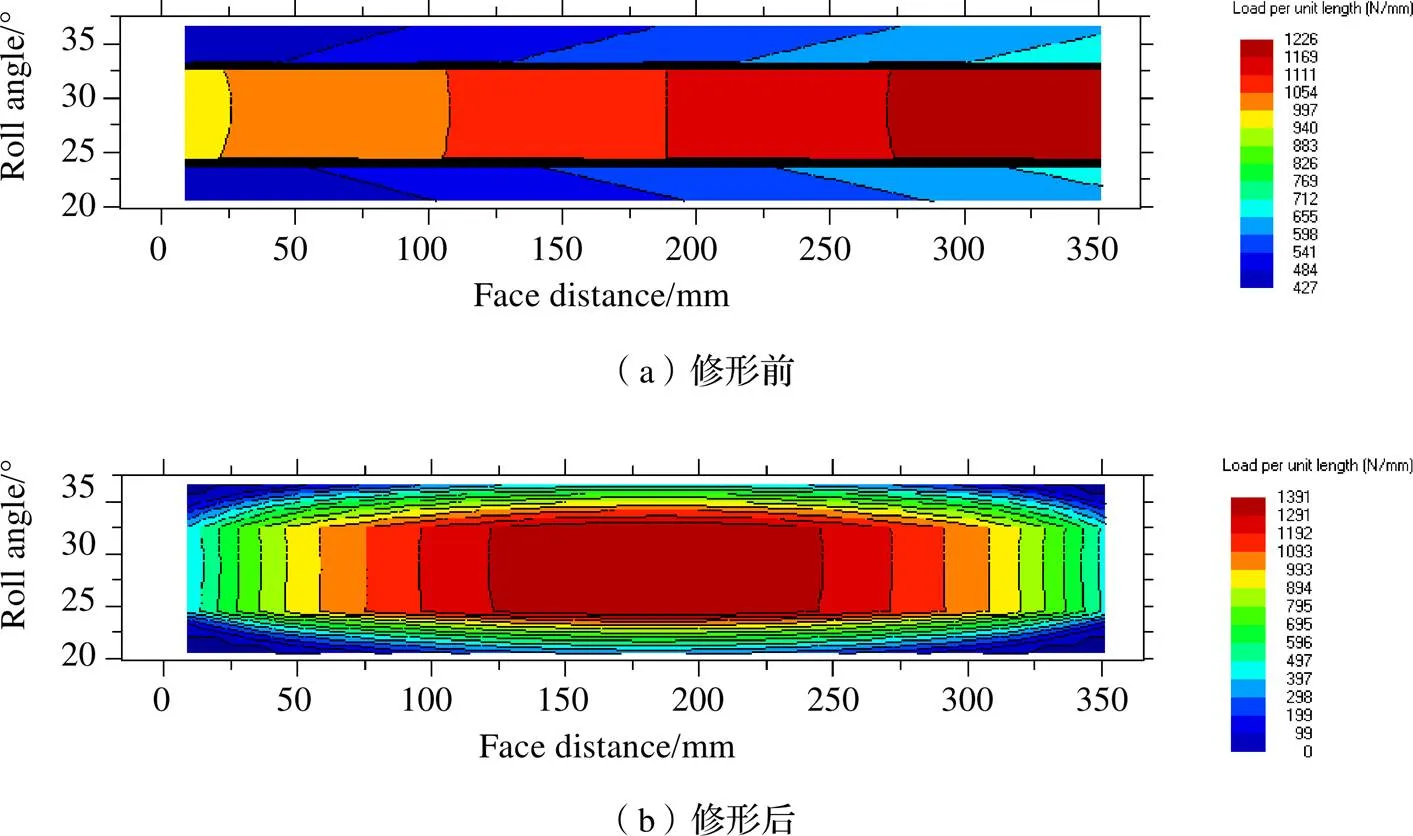
图11 二级外啮合修形前后接触斑

4.4 传动误差

由于齿轮在制造、安装等过程中产生的误差，齿轮在受载后将发生弹性变形，从而导致主从动轮之间不均匀转动，传递误差[12]即为描述齿轮间不均匀转动的重要参数，是反映齿轮系统动态性能的重要指标。显然，传递误差的波动对传动系统的振动、噪音有着重要影响。

分别对比一、二级行星内、外啮合齿轮的传递误差如下。

图12为一级行星内啮合修形前后的传递误差，修形前传递误差约为48 μm，修形后传递误差约为16 μm，比修形前降低了26 μm。图13为一级行星外啮合修形前后的传递误差，修形前传递误差约为44μm，修形后传递误差约为14 μm，比修形前降低了30 μm。

图14为二级行星内啮合修形前后的传递误差，修形前传递误差约为29 μm，修形后传递误差约为11 μm，比修形前降低了18 μm。图15为二级行星外啮合修形前后的传递误差，修形前传递误差约为31 μm，修形后传递误差约为17 μm，比修形前降低了24 μm。

通过对比齿轮副修形前后的传递误差可以发现，齿轮修形虽然不能完全消除传递误差，但可以大幅度减小传递误差，对齿轮的动态性能有极大的改善。

图12 一级内啮合传递误差

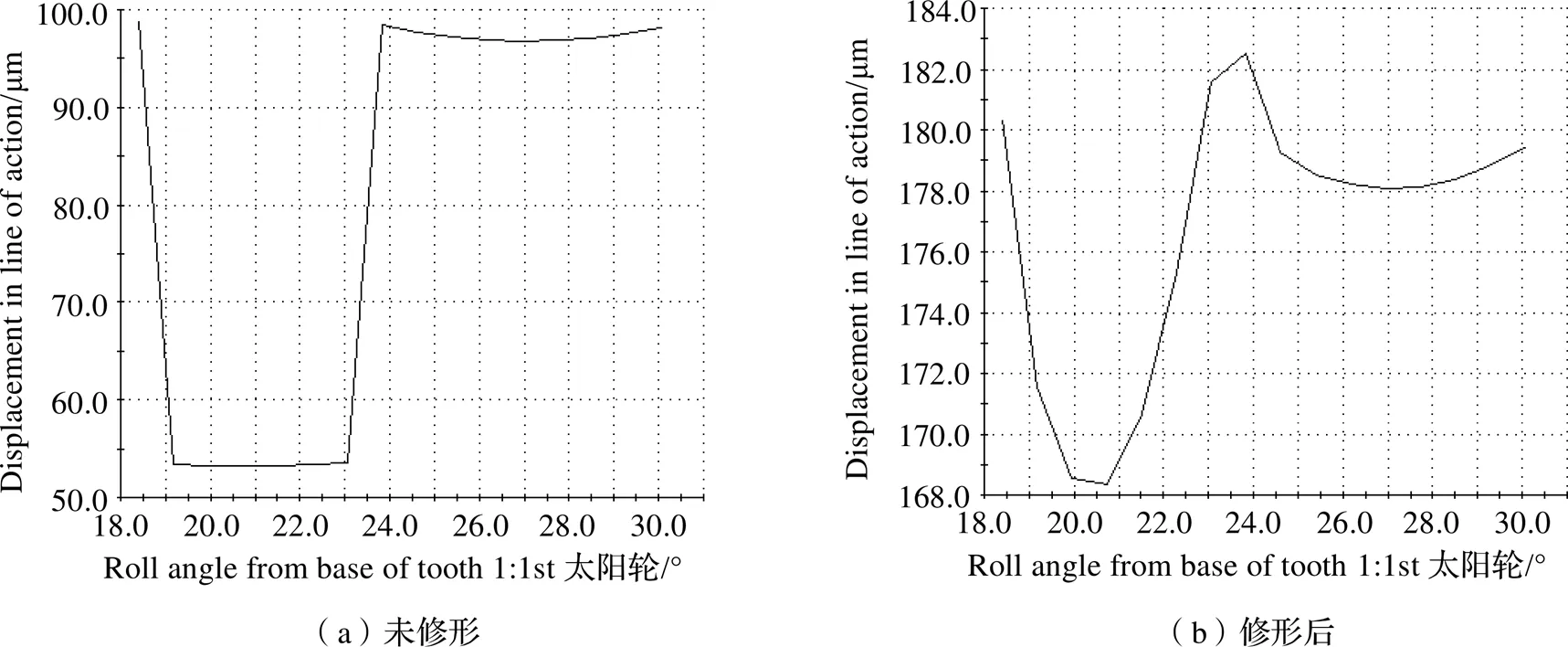
图13 一级外啮合传递误差

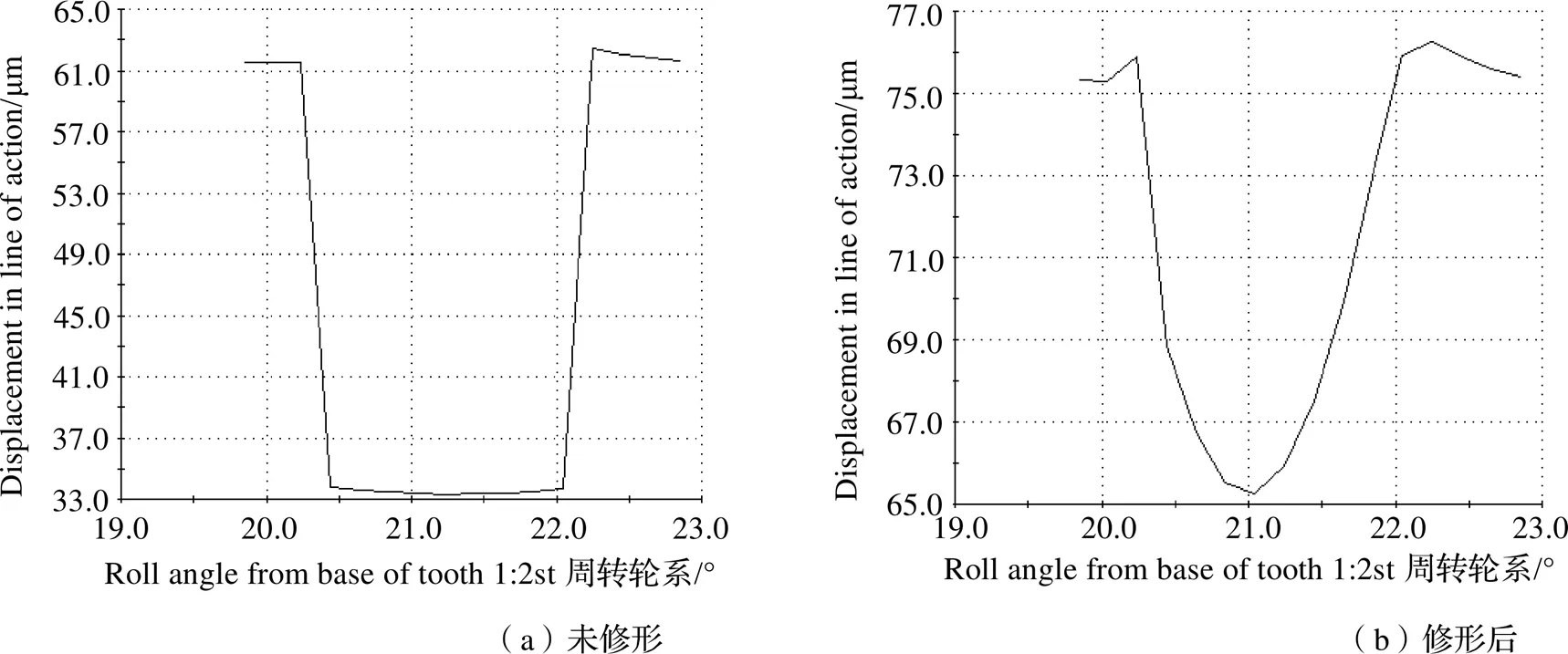
图14 二级内啮合传递误差

5 结论

本文简要介绍了齿轮修形原理以及功率分流齿轮箱的基本结构，通过Romax软件建立了某型号5 MW功率分流齿轮箱传动模型，同时考虑轮毂、发电机外壳对整体模型的影响。对比修形前后内外啮合齿轮接触斑的分布情况，结果显示：修形前，沿齿宽方向承受载荷的宽度约占整个宽度的1/2，且载荷分布极不均匀；修形后，在齿宽方向上，载荷由中间向两边递减，呈对称分布，齿面受载更加均匀，且齿宽方向参与承载的宽度变大了，整个齿宽方向上几乎都有载荷分布，增加了齿轮的承载能力。对比齿轮副修形前后的传递误差可以发现，齿轮修形虽然不能完全消除传递误差，但是可以大幅度减小传递误差，对齿轮的动态性能有极大的改善。

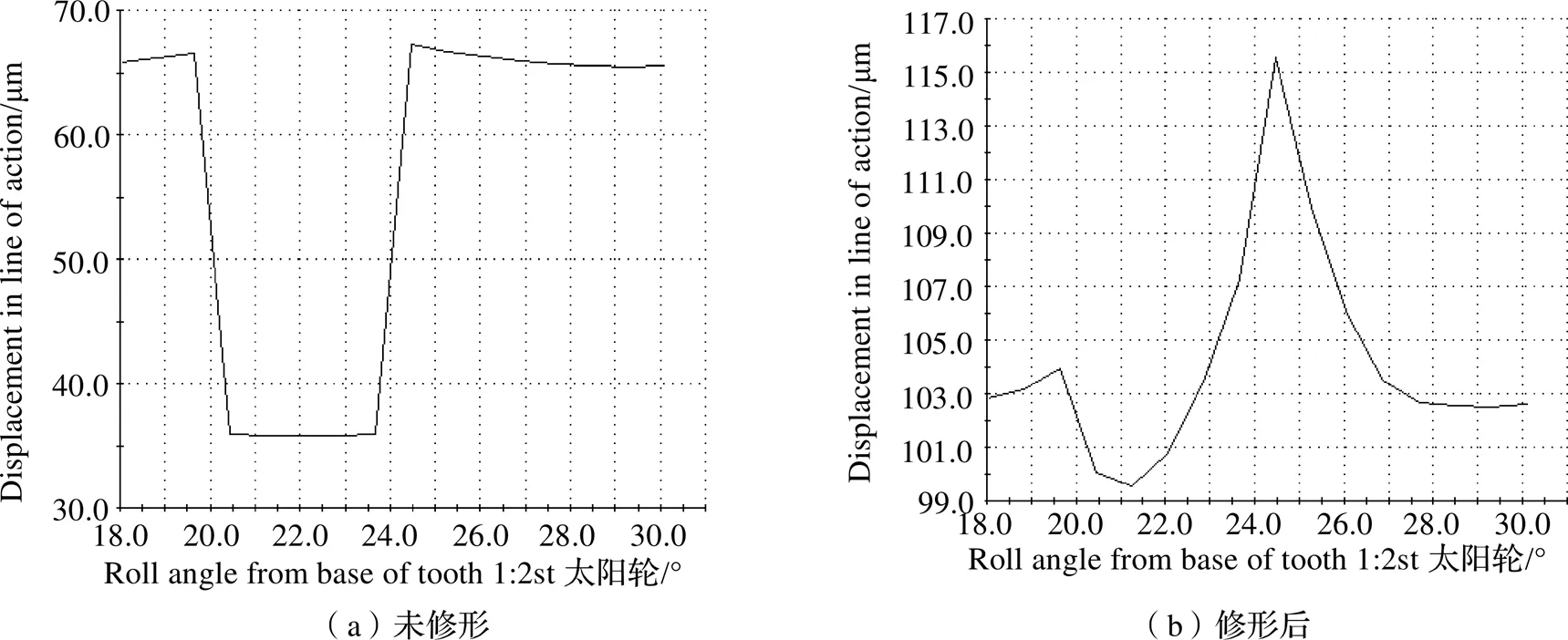
图15 二级外啮合传递误差

[1]GB/T 19073－2018，风力发电机组齿轮箱设计要求[S].

[2]Hsiang Hsi Lin，Fred B. Oswald，Dennis P. Townsend. Dynamic loading of spur gears with linear or parabolic tooth profile modifications[J]. Mechanism & Machine Theory，1989，29（8）：1115-1129.

[3]陈方明，王庆良. 风电齿轮箱齿轮修形设计及研究[J]. 机械传动，2018，42（12）：155-159.

[4]李锐. 轮齿修形对风电增速齿轮箱静动态特性影响分析[D]. 重庆：重庆大学，2019.

[5]范孝良，石鹏飞，刘建民. 风电齿轮箱微观修形对振动与声振粗糙度性能的影响[J]. 中国工程机械学报，2019，17（1）：47-52.

[6]王彬，郭润兰，黄华. 基于Romax下的齿轮仿真分析及优化[J]. 机械制造与自动化，2017（1）：101-104.

[7]方振江，华青松，马文勇，等. 风电增速齿轮箱功率分流和柔性销的设计计算[J]. 机械传动，2016（12）：85-88.

[8]汤亮，何仁杰，龚发云，等. 基于兆瓦级风电齿轮箱传动特性的齿轮修形研究[J]. 武汉大学学报（工学版），2019，52（5）：457-464.

[9]赵昕. 基于KISSsoft软件的风电齿轮箱齿轮修形参数优化设计[J]. 机械工程师，2018，330（12）：44-46.

[10]于印鑫，李宽，郑朋，等. 功率分流式风电机增速箱振动特性分析[J]. 噪声与振动控制，2019，39（6）：19-24.

[11]日本机械学会，著. 李茹贞，赵清慧，译. 齿轮强度设计资料[M]. 北京：机械工业出版社，1984：30-32.

[12]汪建，张俊. 轮齿修形对斜齿轮传递误差影响的比较性分析[J]. 振动与冲击，2018，37（2）：254-260.

Simulation Analysis of Gear Modification of Power Distribution Gearbox Based on Romax

ZHOU Du，ZHENG Chuantong

( Wind Energy Research Institute,MingYang Smart Energy GroupLimited,Zhongshan 528437,China )

Gear modification can effectively reduce gearbox vibration and noise and extend the service life. This paper studies a 5 MW power-split wind power gearbox. Based on the theory of gear modification and the analysis of basic structure of the power shunt wind power gearbox, we establish a 5 MW power-split gearbox model with software Romax. A static simulation analysis of the gearbox is conducted by using the load spectrum, and tooth profile and tooth direction of the first and second stage gears is modified according to the gear load distribution, transmission error and other parameters. With tooth modification, the load sharing characteristic between the gears of the power split type wind power gearbox is realized, and the transmission error of the gears is reduced.

power-split；wind power gearbox；gear modification；Romax；load characteristics

TH131.6

A

10.3969/j.issn.1006-0316.2021.02.010

1006－0316 (2021) 02－0071－10

2020－04－05

周杜（1993－），湖南湘潭人，硕士，工程师，主要从事风电齿轮箱仿真工作，E-mail：zhoudu@mywind.com.cn；郑传统（1981－），四川成都人，硕士，工程师，主要从事风电齿轮箱仿真工作。