六自由度工业搬运机器人的运动特性分析及仿真研究
王哲,孟广耀,孙英暖,王维信
六自由度工业搬运机器人的运动特性分析及仿真研究
王哲,孟广耀*,孙英暖,王维信
(青岛理工大学 机械与汽车工程学院,山东 青岛 266520)
针对目前国内外移动关节在多自由度机器人上研究和应用较少的现状,本文设计了一款具有移动关节的六自由度机器人并将其应用于工业搬运作业。利用MD-H法建立该机器人的运动学模型,并推导出它的正逆运动学公式。在MATLAB软件的Robotics Toolbox平台下建立该机器人的仿真模型对正逆运动学公式进行验证并运用蒙特卡洛法生成它的工作空间点云图。仿真结果表明,该机器人的工作空间变化平缓且无明显空腔,从而说明机器人结构设计的合理性。最后对其轨迹进行分析并生成各关节变量和笛卡尔坐标分量随时间的变化曲线。
移动关节;运动学;蒙特卡洛;工作空间;轨迹分析
自1961年第一台工业机器人Unimate问世以来[1],机器人开始登上现代化生产的舞台。工业机器人不但可以代替人在危险、恶劣的环境下进行作业,而且在某些领域比人工更加精密、高效。近年以来,随着机器人技术的不断发展和完善,机器人在各个行业和领域蓬勃发展起来,如欧美和日本已有服务型机器人投入试验和使用[2]。通过对国内和国外工业机器人生产设计厂家进行研究分析之后发现机器人的运动学、动力学分析和轨迹规划一直是各个机构研究的重点[3]。
机器人的运动学分析是动力学分析、轨迹和路径规划、自动控制的前提和基础[4]。本文提出了一种包括两个移动关节的六自由度搬运机器人结构,应用SolidWorks软件建立了三维实体模型,并对其进行工业搬运过程中的运动特性分析。首先根据其结构特点,利用MD-H法建立运动学模型,通过正逆运动学推导分析它在空间作业过程中关节坐标系和世界坐标系的关系,并应用MATLAB软件中的机器人工具箱进行仿真分析;然后应用蒙特卡洛法求解出它的工作空间点云图;最后设定了它的运动轨迹和运动速度得到其各关节变量和笛卡尔坐标分量随时间的变化曲线。
1 结构设计和运动模型建立
DM06型六自由度机器人有4个旋转关节和2个移动关节共6个关节,根据该机器人工作特点,可以分为旋转模块、伸缩模块和升降模块[5]。旋转关节负责定位,伸缩关节负责改变末端执行器在空间中的位置,升降关节负责对机器人作业高度进行调节。该机器人特点是刚度和精度高,适应在工业生产作业过程中,工厂环境复杂,障碍多的特性。DM06型六自由度机器人结构简图如图1所示。
应用SolidWorks软件建立DM06型六自由度机器人三维模型如图2所示。

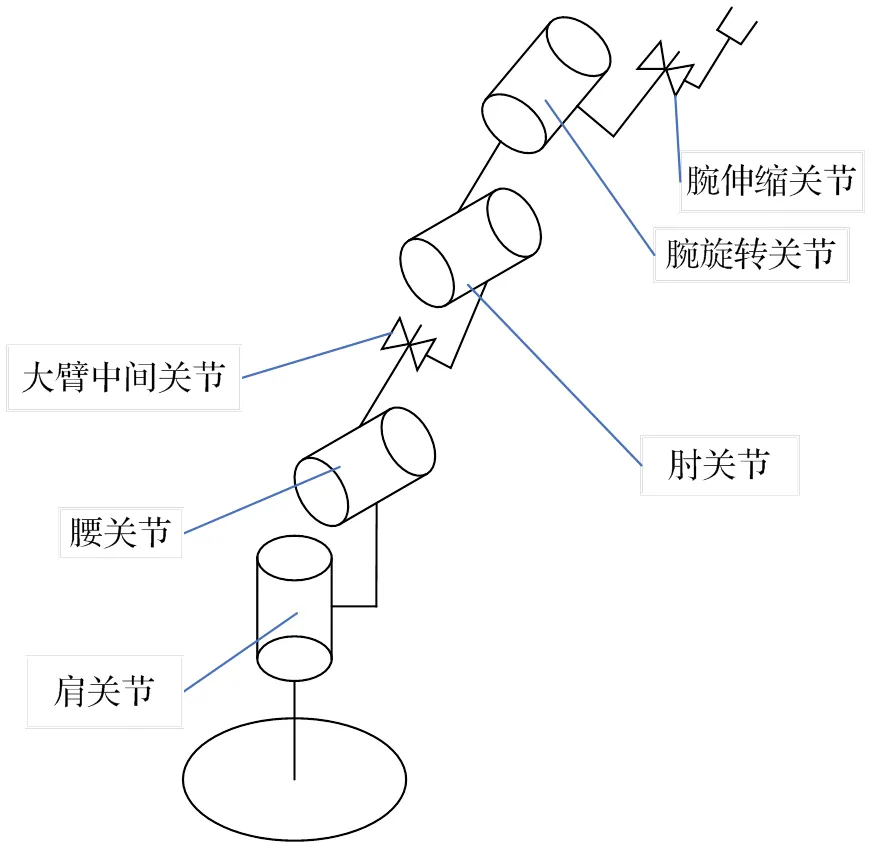
图1 机器人结构简图

图2 DM06型六自由度机器人三维模型
根据所建的坐标系得到DM06型机器人的D-H参数如表1所示,各关节变量取值范围如表2所示。
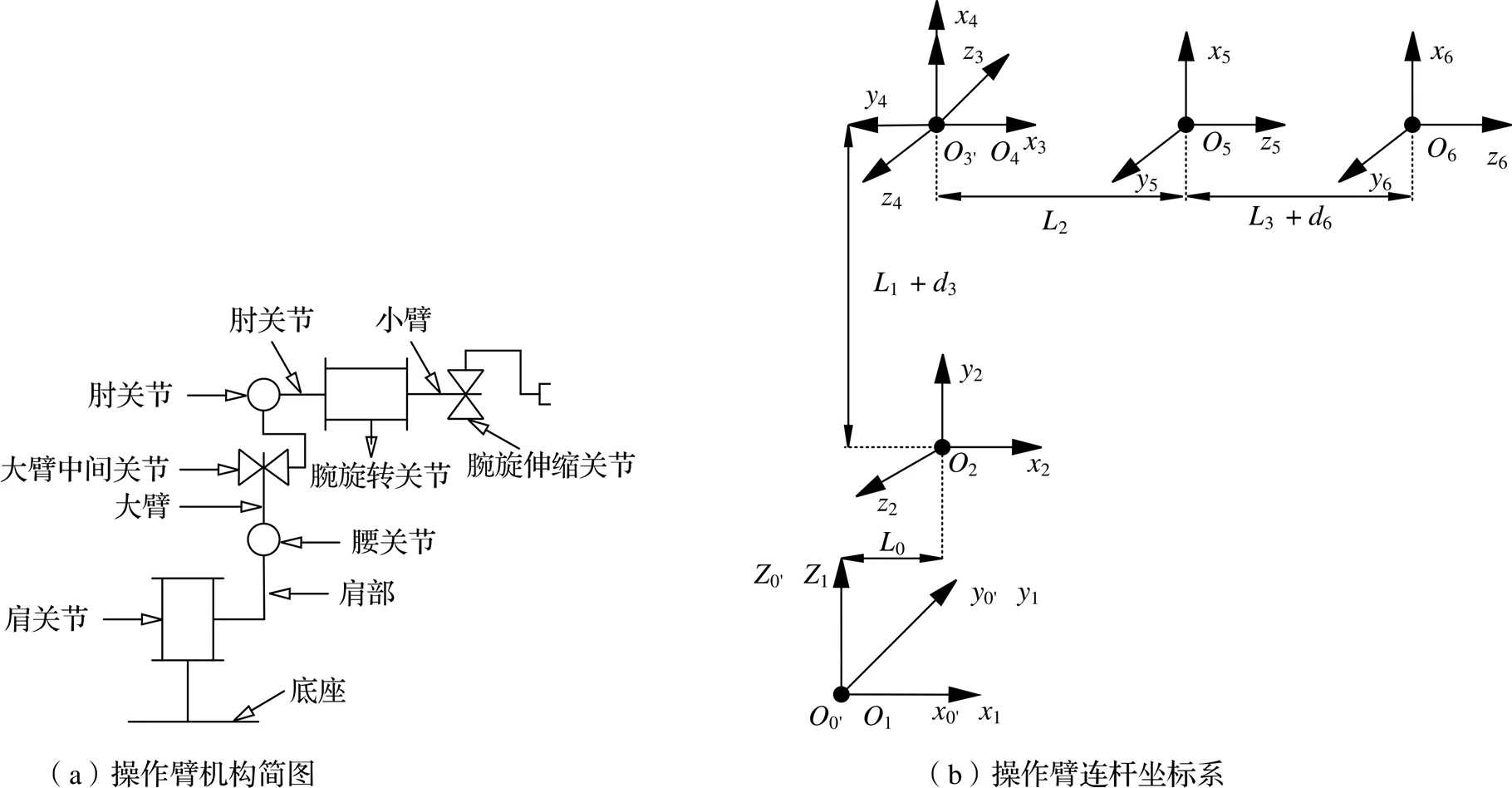
图3 机器人坐标系示意图
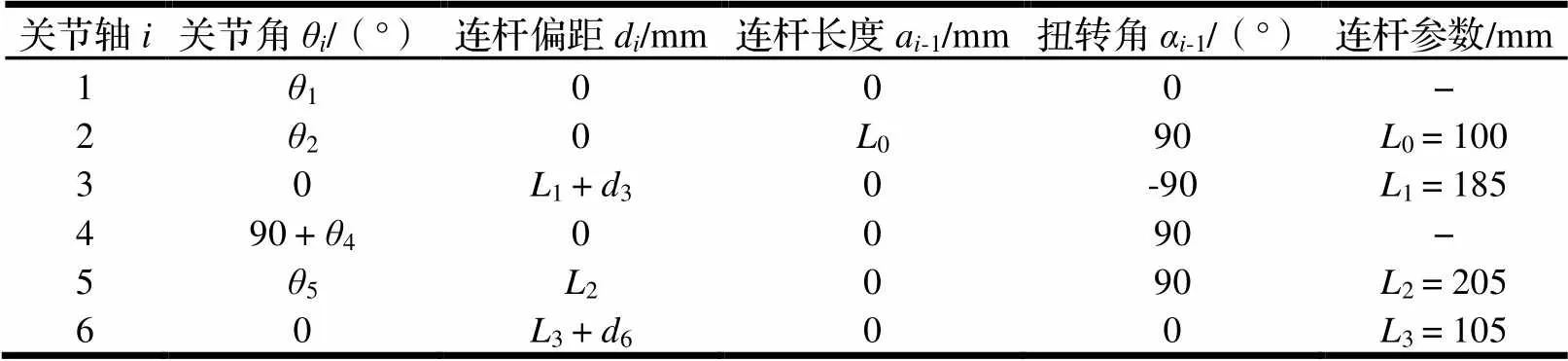
表1 DM06机器人的MD-H杆件坐标系参数

表2 关节变量取值范围
2 运动学求解
2.1 正运动学推导


在式(1)基础上可以得到连杆变换矩阵的一般表达式为:
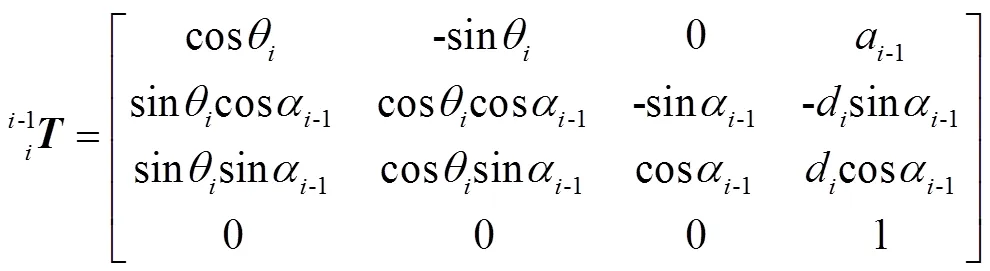
可以看出连杆变换矩阵取决于四个参数θ、d、a-1和α-1,其中只有一个参数是变动的,在旋转关节中θ是关节变量,而在移动关节中d是关节变量。将两者统一起来,θ表示第个关节变量,对于移动关节,令θ=d[1]。

其中各关节变换矩阵如下:


式中:sθ=sinθ、cθ=cosθ。
将各个矩阵按顺序相乘,就可以得到该机器人的正运动学方程为:

式中:


2.2 逆运动学推导
机器人的逆运动学是机器人运动学十分重要的一部分,它是控制机器人运动轨迹的基础。机器人的运动学反解在多数情况下具有多重解,有时也会出现解不存在的情况。在求运动学反解的过程中仅仅将解求出来是不够的,还需保证计算的精度和效率,其中得到封闭解是最为理想的情况。求机器人的运动学反解是指解出末端执行器到达空间某一确定的位置的全部姿态,所以在出现多种解的状况下需要解出所有的解,这种要求一般的迭代方法并不能达到,所以不适用于求机器人的运动学反解[1]。得到封闭解的一般途径有代数法和几何法两种,本文采用应用较为普遍的代数方法——反变换法来求解DM06型机器人的运动学反解。因为机器人的正向运动学是唯一确定的,在给定确定的关节变量之后求得的机器人末端的空间位置和姿态矩阵(,,,),可以利用左乘逆矩阵的方法来反求机器人的逆运动学,这种方法就是反变换法。


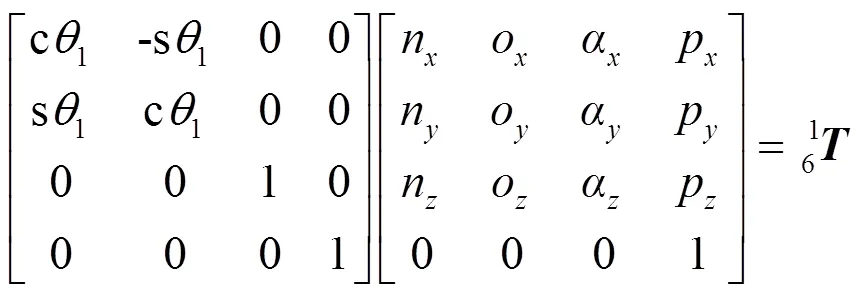
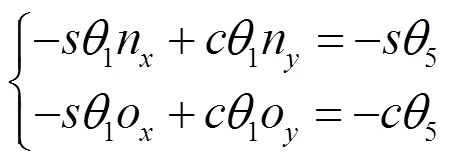
由三角变换解得:
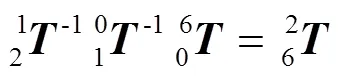
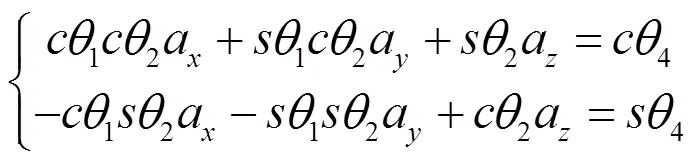
由此可求得2和4的解。
再由第4列,令矩阵元素两端对应相等可得到关于6的方程为:

只要4≠0,便可解得:
当4=0时,操作臂处于奇异形位[1]。此时关节轴线3和6重合,方程组个数少于未知量个数,只能解出3和6的和或差。当操作臂处于奇异形位时,可在6的变化范围内任意取值,再求得相应的3的值。

解得:
至此,DM06六自由度机器人的运动学逆解全部求解完成。由于该机器人的关节变换矩阵和求解方程非常复杂[8],从而导致该机器人的逆运动学存在多种解,但是由于结构的限制,这些解不可能都实现。机器人在作业过程中,应选择在关节变量范围内,消耗功率最少、最短行程、受力最小、能越过障碍物等条件下的最优的一组逆解[1]。
3 MATLAB仿真验证
3.1 结果验证
在DMO6机器人的关节变量取值范围内选取四组典型的关节变量如表3所示。
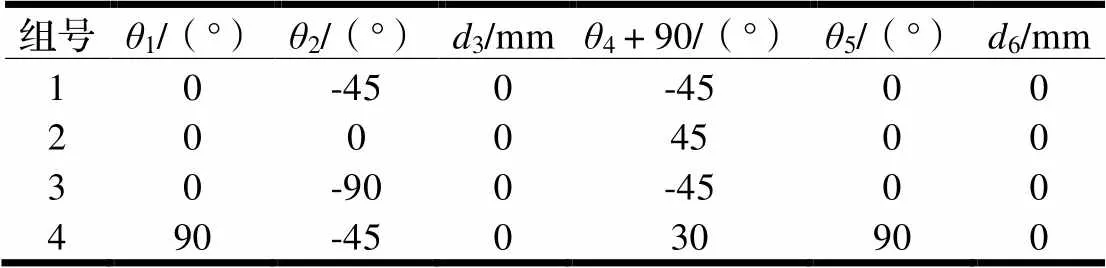
表3 四组关节变量值
将表3数据代入式(4)分别得到四组关节变量的正运动学解为:



利用MATLAB中自带的正运动学计算函数fkine计算四组关节变量的正解发现与根据式(4)计算的正解结果一致,说明正运动学求解公式正确[7]。
逆运动学的算法验证:在关节变量变化范围内任意给定三组关节变量,按正运动学算法计算末端位姿矩阵;计算得到的末端位姿矩阵代入逆运动学算法,求得各关节变量,若与给定的关节变量相等,即可说明逆运动学算法的正确性。给定的三组关节变量与求得的逆解如表4所示。
当给定的关节变量为特殊三角函数值时,第1组的逆解值与给定关节变量相等,其它两组的逆解值也与给定关节变量基本一致,说明文中推导的逆解公式是正确的[8]。

表4 给定的关节变量和逆解值
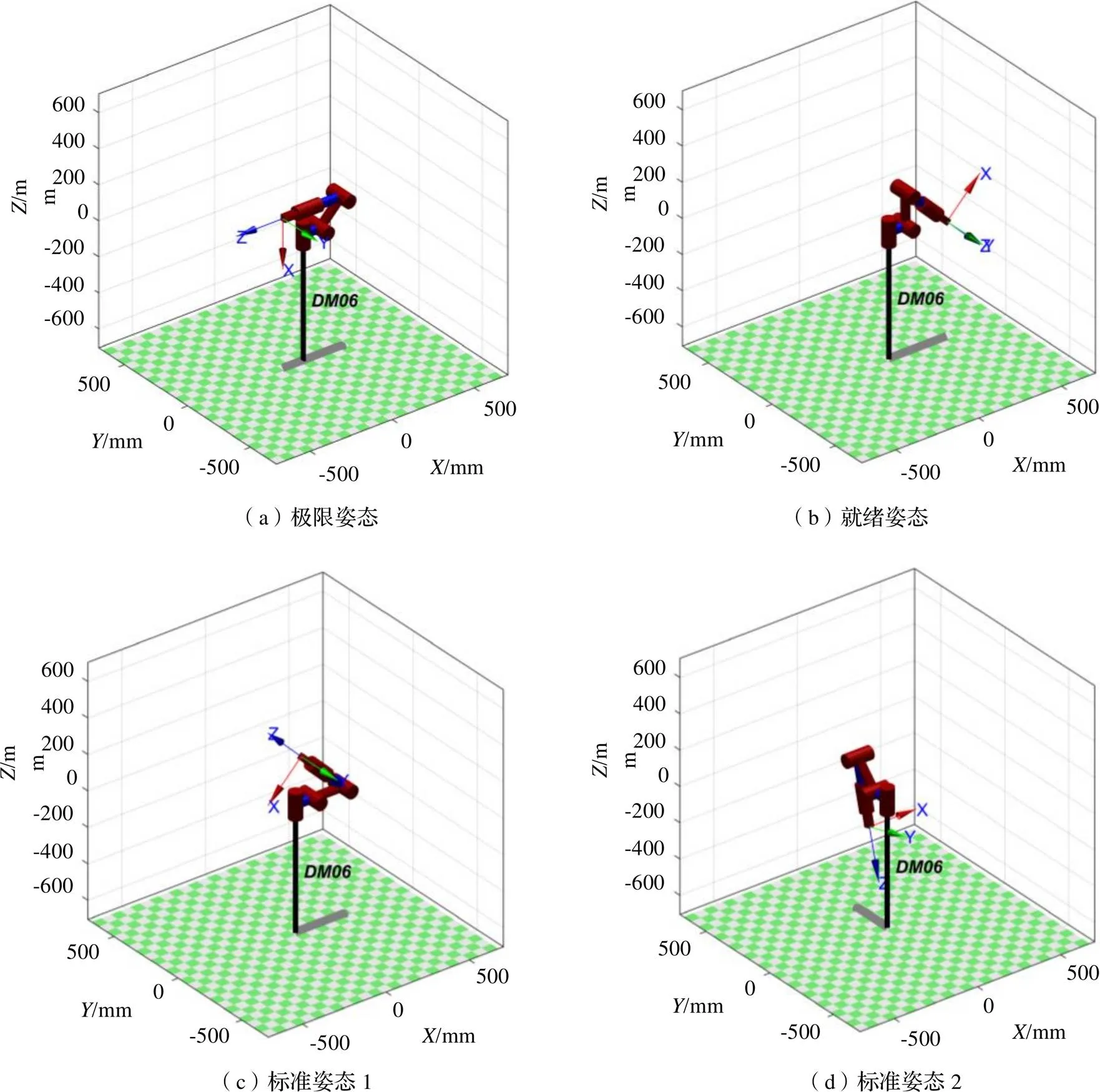
图4 DM06机器人位置姿态
3.2 工作空间仿真
机器人的工作空间一般是指机器人末端执行器在空间作业时所能达到所有点的集合,由于末端执行器是可以与机器人任意组合,所以本文求解的工作空间指的是末端关节在空间作业时能达到所有点的结合。机器人工作空间的求解方式由多种,应用较为广泛几何绘图法、解析法和数值法。本文采用蒙特卡洛法来对机器人工作空间进行仿真。蒙特卡洛法是通过随机抽样的方法来求解数学问题,求解步骤如下:
(1)根据正运动学求得末端关节的位姿(,,,)。
(2)应用MATLAB软件中的rand()函数产生关节变量的随机值[9]:
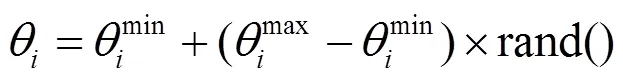
(3)利用机器人工具箱中的kfine()函数产生运动学正解,带入关节变量求得末端位置。
(4)生成所有随机位置点的集合,便形成了机器人工作空间的点云图。
蒙特卡洛法求解机器人工作空间的精度与样本所取随机样本数有关[10],一般情况下所取随机样本数越大,求解的精度也就越高。文中选取随机样本数=30000,利用蒙特卡洛法在机器人的各个关节变量中产生30000组随机数,并计算出每组变量下的末端位姿,绘制出机器人的工作空间立体图如图5所示。
为了更清楚地观察机器人的工作空间,在MATLAB软件中分别得到工作空间在、、三个平面的投影如图6所示,并提取末端关节在空间作业时、、方向的极限尺寸如表5,所示。

图5 三维工作空间
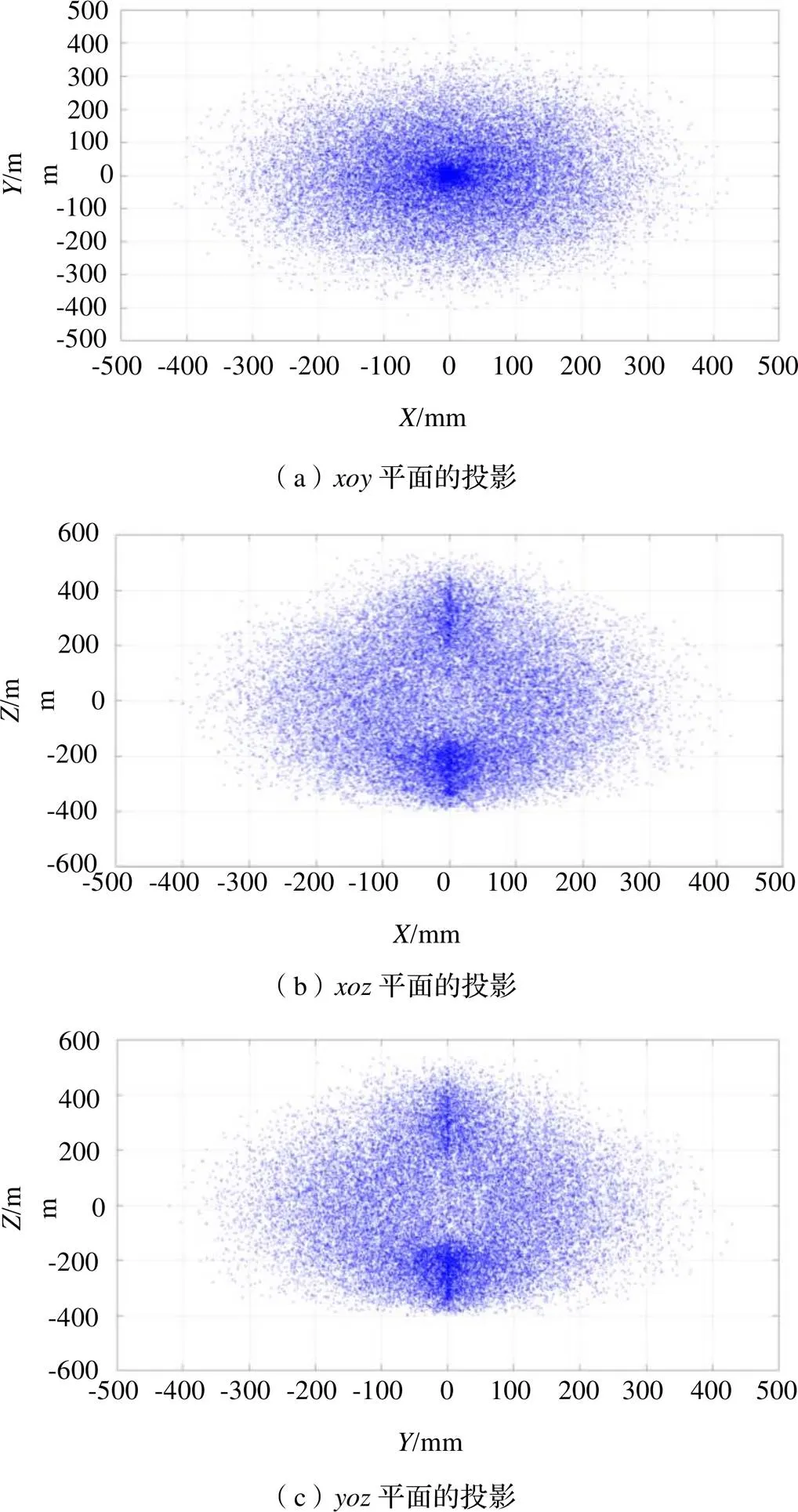
图6 机器人工作空间在xoy、xoz、yoz三个平面的投影
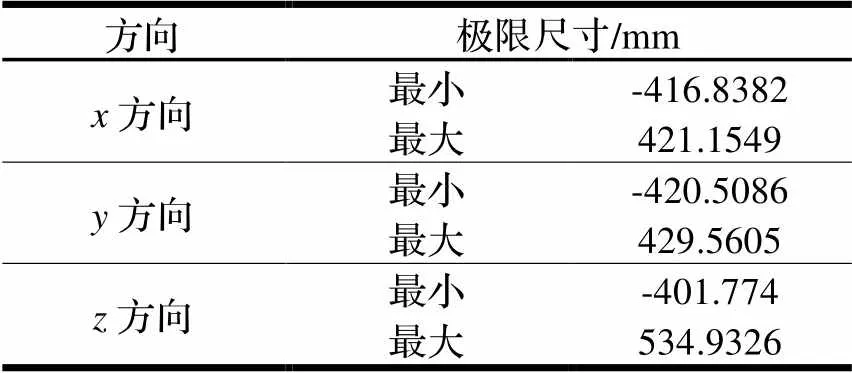
表5 点云极限尺寸
从仿真结果上看,该机器人的工作空间类似一个球体,变化平缓,工作点分布集中。在符合该机器人结构设计下的各关节变量范围内形成的工作空间没有明显的空洞,说明该机器人结构设计合理并且仿真结果符合机器人实际工作空间[11]。
4 末端执行器轨迹规划及速度控制
将机器人末端执行器由位姿1移动到位姿2是机器人运动学的基本要求。末端执行器轨迹曲线可在关节空间和笛卡尔空间中生成。本节使用第3节的关节变量3和关节变量4使末端执行器在两形位之间生成关节空间轨迹,使用标量插补函数配合优化后的多轴驱动函数生成轨迹,整个过程2 s内完成,采样时间间隔为50 μs,如图7所示。导致机器人姿态与标准姿态2有差异的原因是逆运动学存在多种解,但达到的工作点位置一致。
分别得到机器人末端执行器轨迹运动过程中6个关节变量随时间变化图像和随时间变化的笛卡尔坐标分量如图8、图9所示。

图7 末端执行器运动轨迹
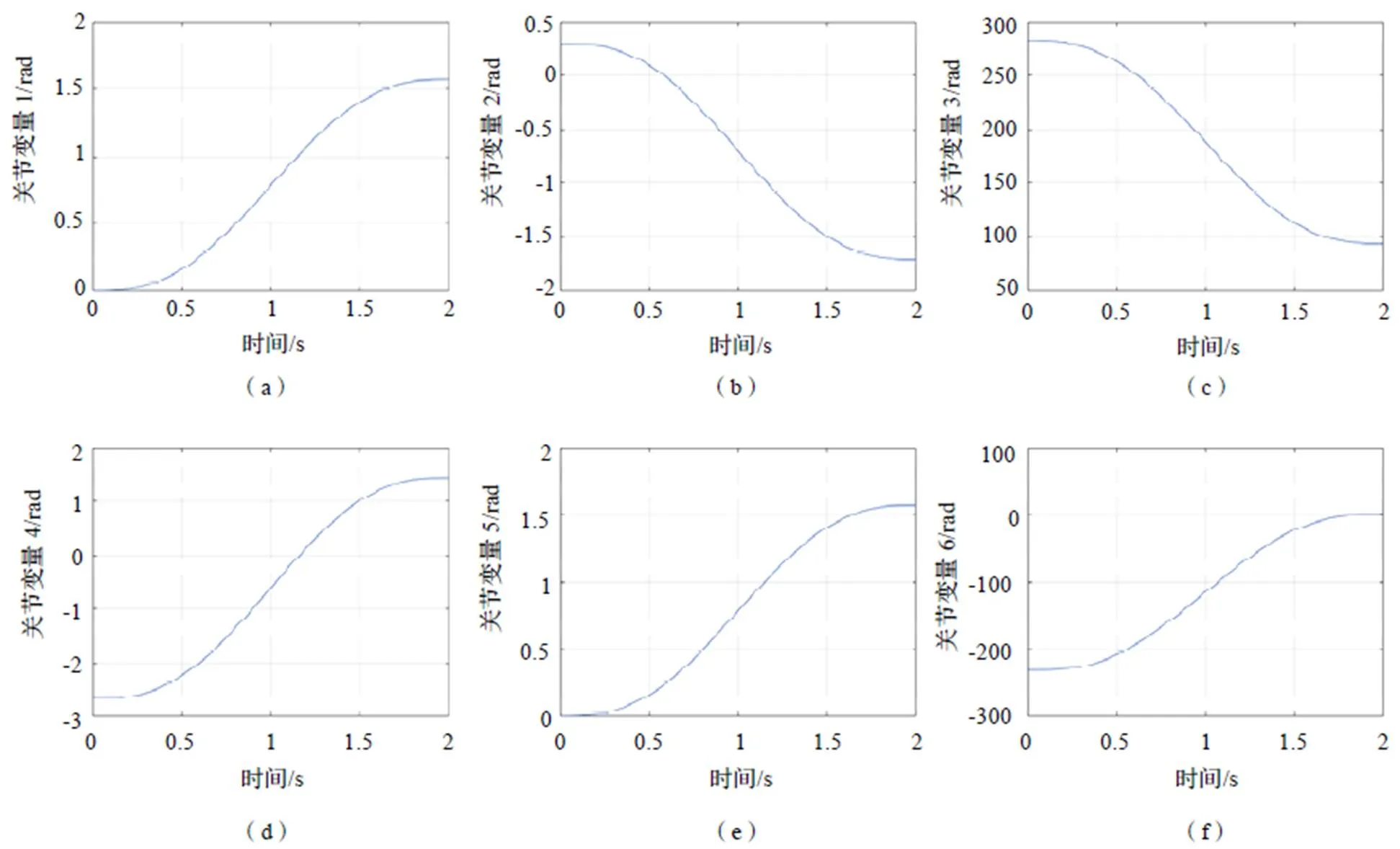
图8 六个关节变量随时间变化图像

图9 随时间变化的笛卡尔坐标分量
5 结论
(1)结合实际完成了六自由度搬运机器人的结构设计,利用SolidWorks软件建立了该机器人的三维模型。根据其结构特点利用MD-H法建立了机器人的运动学模型,并通过坐标变换和反变换法分别推导出正逆运动学公式。分析了机器人搬运作业时的末端连杆坐标系、工具坐标系和世界坐标系的位姿关系。
(2)利用MATLAB中的机器人工具箱建立机器人仿真模型对文中正逆运动学公式进行验证并运用蒙特卡洛方法进行了机器人的工作空间的仿真分析,并提取了末端关节运动的极限尺寸。结果显示机器人工作空间结构紧凑,无明显的空洞和空腔,证明机器人的结构设计是合理的。
(3)设定机器人末端执行器的运动轨迹和运行速度,生成了各关节变量和笛卡尔坐标分量随时间的变化曲线。
[1]熊有伦,李文龙,陈文斌. 机器人学:建模、控制与视觉[M].武汉:华中科技大学出版社,2018:93-107.
[2]Antonio Lopez Pelaez,Dimitris Kyriako. Robots genes and bytes technology development and social changes towards the year 2020[J]. Technological Forecasting & Social Change,2008(75):1176-1201.
[3]南永博. 六自由度搬运机器人运动轨迹规划及仿真分析[D]. 汉中:陕西理工大学,2018.
[4]陈勉. 前后大臂偏置式七自由度工业机器人本体设计与仿真优化[D]. 杭州:浙江大学,2016.
[5]郑华,陈军,金鸿章. SCARA机器人运动学和视觉抓取研究[J].组合机床与自动化加工技术,2017(6):50-53,58.
[6]John J. Craig. Introduction to robotics:mechanics and control,fourth edition[M]. San Francisco:Pearson Education,2005:13-90.
[7]程堂灿,张凤生,王浩. 基于MATLAB的采摘机器人运动特性分析与仿真研究[J]. 机床与液压,2019,47(11):29-34.
[8]左骏秋,张磊,喜冠南,等. 关节半解耦6自由度服务机器人的设计与运动学研究[J]. 机械设计,2017,34(6):88-94.
[9]徐小龙,高锦宏,王殿君,等. 基于MATLAB的七自由度机器人运动学及工作空间仿真[J]. 新技术新工艺,2014(5):21-24.
[10]宁祎,陈志苓. 基于Matlab的七自由度机械手逆运动学分析及仿真[J]. 科学技术与工程,2012,12(7):1522-1525.
[11]熊艳梅,杨延栋.码垛机器人运动学分析与仿真[J]. 机械,2015,42(1):62-66.
Analysis and Simulation of the Motion Characteristics of a 6-DOF Industrial Handling Robot
WANG Zhe,MENG Guangyao,SUN Yingnuan,WANG Weixin
( School of Mechanical and Automotive Engineering, Qingdao University of Technology, Qingdao 266520, China )
In view of the lack of the research and application of mobile joints at home and abroad on multi-degree-of-freedom robots, a six-degree-of-freedom robot with mobile joints is designed and applied to industrial handling operations. The kinematics model of the robot is established by MD-H method, and its forward and inverse kinematics formulas are derived. The simulation model of the robot is built on the Robotics Toolbox platform of MATLAB software to verify the forward and inverse kinematics formulas and its workspace point cloud image is generated through the Monte Carlo method. The simulation result shows that the working space of the robot changes smoothly and there is no obvious cavity, which demonstrates the rationality of the structural design of the robot. Finally, the trajectory is analyzed and the time-varying curve of each joint variable and Cartesian coordinate component is generated.
mobile joint;kinematics;Monte Carlo;workspace;trajectory analysis
TP242.2
A
10.3969/j.issn.1006-0316.2021.02.005
1006-0316 (2021) 02-0032-10
2020-08-07
国家自然基金项目(51175276)
王哲(1996-),男,山东青岛人,硕士研究生,主要研究方向为先进制造(32*-)技术与装备、机器人技术。*通讯作者:孟广耀(1963-),男,辽宁本溪人,博士,教授,主要研究方向为切削磨削技术、先进制造技术与系统、农业机械系统,E-mai:gymeng1963@163.com。

