硬质合金刀具前刀面粘结破损形貌的自由能分析

郑敏利 ，陈保良 ，陈金国 ，2，张 为

（1“.哈尔滨理工大学高效切削及刀具”国家地方联合工程重点实验室，黑龙江 哈尔滨 150080；2.莆田学院机电工程学院，福建 莆田 351100）

1 引言

2.25CrlMo0.25V 钢是常见的难加工材料，由于其具有高硬度、加工硬化严重、热导率低、材料亲和性大、含有硬质点等特点，切削时刀具粘结破损严重。国内外很多学者对刀具粘结破损进行了研究。文献[1]在仿真分析与试验分析的基础上对极端重载切削条件下刀－屑粘结失效进行分析，发现切削区域的波动热－机械耦合是引起刀－屑粘结失效的主要因素。同时从原子间的扩散和再结晶的角度研究切削2.25CrlMo0.25V 钢时刀－屑间的粘焊破损机理，并指出选用超细晶粒硬质合金刀具是解决粘刀问题的途径之一。以研究刀－屑粘结形成实质为目的，在元素扩散试验的基础上对硬质合金刀具粘结破损机理进行研究与分析。在粘结破损试验的基础上，建立了温度与粘结破损深度之间的数学理论模型，分析温度与粘结破损之间的关系。从温度的角度对铣刀片温度场进行有限元分析，通过对温度场的模糊综合评判，预测了波形刃铣刀片抗粘结破损的优越性能[1－5]。文献[6]应用有限元分析法分析了粘结破损时热—力耦合后的等效合成应力，并指出改变槽型是提高抗粘结破损的有效方法。同时分析了不同条件下粘结破损的发生情况，揭示了铣刀片发生粘结破损的主要原因[6－7]。Slter 和Gulpak 建立了热通量分布回归模型，通过正交实验发现刀具的粘结破损绝大多数发生在高温高压的环境下，并且热通量不仅取决于热量值，也取决于切削过程中的切削速度和切削深度[8]。这些研究都证实了硬质合金刀具与切屑之间发生粘结破损的条件是复杂的，切削过程中力－热温度耦合作用是影响硬质合金刀具粘结破损的重要因素。

在切削加工过程中，粘结破损是一种非正常的磨损。对粘结破损进行研究，就是对非平衡态和不可逆过程进行分析，为了延伸经典热力学的概念和方法，使其能够用于研究分析非平衡态和不可逆过程，需要对经典热力学做出一些假设。因此用热力学理论和方法对其进行研究是合理可行的。国内外不少学者从吉布斯自由能的角度对材料的热变形与磨损进行研究。文献[9]利用吉布斯自由能判据分析硬质合金刀具在切削过程中扩散反应的发生规律，发现WC 含量较多的硬质合金刀具更适合于高速切削，在一定程度上减轻刀具的扩散磨损。文献[10]针对涂层刀具切削性能和失效机理进行研究，利用吉布斯自由能函数计算可涂层刀具材料和镍基合金在切削过程中可能发生的反应，结果表明刀具材料和工件材料在切削过程中都有不同程度的氧化反应，刀具材料组份和镍基合金基体元素Ni 在800K 不会发生化学反应，相容性较好。文献[11]基于不可逆过程热力学的基本理论，建立了固体损伤理论，为从热力学角度研究刀具磨损破损提供了的基础。文献[12－14]在拉格朗日－吉布斯理论基础上提出均匀、各向同性有限热变形本构理论，并指出自由能不等式外部场仅存在于空间C 的有限区域中，文献[15]利用粒状材料吉布斯自由能来确定梯度内的数量，解决了平衡状态下粒状介质连续模型的可积性问题。文献[16]运用改进的吉布斯准化学模型，精确计算了钢液中溶质的吉布斯自由能。文献[17]建立了TiC 涂层反应和切削过程中物质相变的自由能模型，运用Matlab 软件分析了TiC 涂层自由能变化与温度曲线。目前，相关学者在自由能的研究方面较少涉及到刀具的粘结破损，应用热力学理论，建立刀－屑接触区熵变、焓变的理论模型，并将其进行整合建立刀－屑接触区粘结自由能理论模型。结合实验数据，将理论模型的计算结果进行数据拟合，在不同切削参数的条件下，分析粘结自由能和刀具粘结破损之间的关系，在自由能的角度对刀具的粘结破损进行研究。

2 粘结自由能模型的建立

2.1 刀－屑接触区熵理论模型

熵在热力学中是反应物质系统混乱度的一种物理量，能够反映热量传递的方向。熵与能量在空间中分布的均匀程度有关，熵越大，能量分布越均匀。在金属切削过程中，刀具会受到较高的机械应力、热应力和热冲击。在这种力－热耦合的作用下，刀－屑接触区发生粘结破损。同时在刀具与工件组成的系统中，能量随着切削过程的进行是不断变化的。因此，熵可以用来描述硬质合金刀具切削2.25Cr1Mo0.25V 时刀－屑粘结破损的程度及粘结破损进行的方向。同时，熵也是自由能模型组成的一部分，其基本定义式为：

式中：J—热力学流（J）；

X—热力学力（N）。

由于粘结破损发生在刀具前刀面，因此需要对第一变形区的剪切面进行受力分析，第一变形区剪切面受力图，如图1 所示。分析后可得前刀面的摩擦力Fγ的表达式为：

单位时间内切削金属产生摩擦功Pλ表达式：

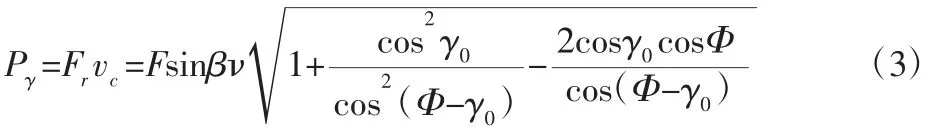
式中：vc—切屑沿前刀面流出速度（m/s）。

将单位时间内切削金属产生的摩擦功定义为热力学流J，前刀面的摩擦力Fγ定义为热力学力X，则可以建立出单位时间内刀－屑接触区熵理论模型为：

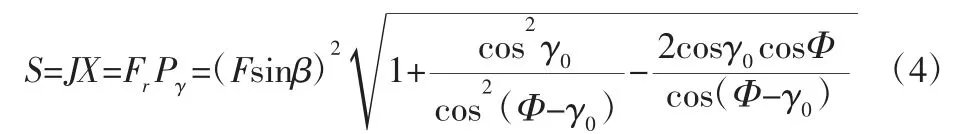
式中：β—摩擦角（°）；γ0—刀具前角（°）；φ—剪切角（°）。

图1 第一变形区剪切面受力图Fig.1 Force Diagram of the Shear Plane of the First Deformation Zone

2.2 刀－屑接触区焓理论模型

焓是表征物质系统能量的状态参数，是由状态参数压力P与体积V的乘积以及系统内能U组成的复合量。焓本身是一个客观存在的状态参数，是一个具有能量属性的状态参数。系统的焓变与路径无关，只与系统的始末状态有关。并且焓也是自由能模型组成的一部分，其基本定义式为：

式中：U—系统内能（J）；P—系统压力（MPa）；V—系统体积（m3）。

硬质合金刀具切削2.25CrlMo0.25V 时，随着刀－屑接触区的内能的动态变化，前刀面的粘结破损体积也在发生变化。刀－屑接触区的内能由三部分构成：切屑与前刀面相互摩擦产生的热量、剪切滑移区剪切产生的热量和后刀面与已加工表面相互摩擦产生的热量。单位时间内各区产生热量的表达式为：

式中：Qc—前刀面接触区产生的热量（J）；

Qs—剪切区产生的热量（J）；

Qf—后刀面接触区产生的热量（J）；

vs—剪切面的剪切速度（m/s）；

Fs—剪切力（N）；

Ff—后刀面摩擦力（N）；

Fc—主切削力（N）。

刀-屑接触区内能的表达式为：

则刀具前刀面接触区焓的表达式为：

式中：λs—剪切区热流比；λc—前刀面接触区热流比；λf—后刀面接触区热流比；Af—刀-屑接触区面积（mm2）。

2.3 刀－屑接触区粘结自由能理论模型

自由能是能够表征系统状态的状态函数，系统的自由能随着体系状态的变化而变化。自由能在不同的应用领域具有不同的含义。硬质合金刀具切削2.25Cr1Mo0.25V 时，刀-屑接触区的自由能绝对值可以反映刀-屑接触区中粘结破损驱动力的大小，从而反映前刀面的粘结破损程度。刀-屑接触区粘结破损自由能函数的表达式为：

式中：U—刀-屑接触区内能（J）；P—刀-屑接触区正压力（MPa）；V—粘结破损体积（m3）；T—刀-屑接触区温度（K）；H—刀-屑接触区焓变（J）；S—刀-屑接触区熵变（J）。

将熵、焓理论模型进行整合推导，可得出刀-屑接触区粘结自由能理论模型：

3 粘结破损实验

3.1 实验材料与设备

实验刀具采用硬质合金YT15 方刀片，工件为2.25CrlMo0.25V钢，工件规格为圆棒料，车削加工，切削方式为干切削。实验过程中，对X、Y、Z轴三个方向的切削力和与刀屑温度进行采集，同时利用高速摄影机对粘结过程进行实时拍摄。实验装置，如图2 所示。实验仪器设备，如表1 所示。

图2 实验装置示意图Fig.2 Schematic Diagram of Experiment Device

表1 仪器设备信息Tab.1 Instruments and Models

3.2 实验方法与结果

为了获取切削速度、进给量和背吃刀量单个因素下刀具粘结破损形貌的数据，进行了单因素实验，单因素实验分别测量了切削力、切削温度、粘结体积、粘结深度和粘结面积。切削用量参数范围，如表2 所示。利用超景深显微镜对切削后的刀片进行粘结体积、粘结深度和粘结面积的测量。将测量获取的粘结形貌数据与切削实验获得的相应数据进行整合。实验获得的数据结果，如表3～表5 所示。超景深显微镜，如图3 所示。

表2 切削用量取值范围Tab.2 Range of Cutting Parameters

表3 不同切削速度下力、热及粘结破损形貌实验结果Tab.3 Experimental Results of Force、Heat and Bond Breakage Morphology Under Different Speed

表4 不同进给量下力、热及粘结破损形貌实验结果Tab.4 Experimental Results of Force、Heat and Bond Breakage Morphology Under Different Feed

表5 不同背吃刀量下力、热及粘结破损形貌实验结果Tab.5 Experimental Results of Force、Heat and Bond Breakage Morphology Under Different Cutting Depth

图3 超景深显微镜Fig.3 Optical Microscope with Large Depth of Field

4 粘结破损形貌的自由能分析

4.1 不同切削速度下粘结破损形貌自由能分析

粘结自由能的绝对值能够反映粘结破损驱动力的大小，粘结破损过程的驱动力随着粘结自由能绝对值的增大而增大，粘结破损驱动力越大，粘结破损越容易发生或粘结破损越严重；粘结破损过程的驱动力随着粘结自由能绝对值的减小而减小，粘结破损驱动力越小，粘结破损越不容易发生或粘结破损的程度越轻。

利用Matlab 软件对不同切削参数下刀具粘结破损三维形貌自由能绝对值进行分析，自由能随切削速度的变化规律，如图4所示。其中，在切削过程中不同切削速度的自由能，分析可知，自由能随切削速度ν 先增大后减小，在ν=70 m/min 时自由能G达到最大值，之后自由能G呈现减小的趋势，粘结驱动力越小，粘结破损量越小，前刀面粘结破损程度越轻，如图4（a）所示。不同切削速度ν 和不同粘结面积S下自由能G的三维拟合曲面，由图4（b）可以发现，刀－屑接触区的自由能随切削速度和粘结破损面积的增大呈现先增大后减小的趋势，且三维曲面呈U 型，自由能有最小值无最大值，如图4（b）所示。不同切削速度ν 和不同粘结体积V下自由能G 拟合的三维曲面，由图4（c）可以发现，刀－屑接触区的自由能随切削速度和粘结破损体积不断增大的呈现出先增大后减小的变化，但变化率与图4（b）比较相对平缓，且三维曲面呈S 型，自由能有最小值和无最大值，如图4（c）所示。不同切削速度ν 和不同粘结破损深度H 下自由能G拟合的三维曲面，研究图4（d）可以发现，刀－屑接触区的自由能随切削速度和粘结破损深度的增大呈现先增大后减小的变化，且三维曲面呈S型，自由能有最大值无最小值，如图4（d）所示。

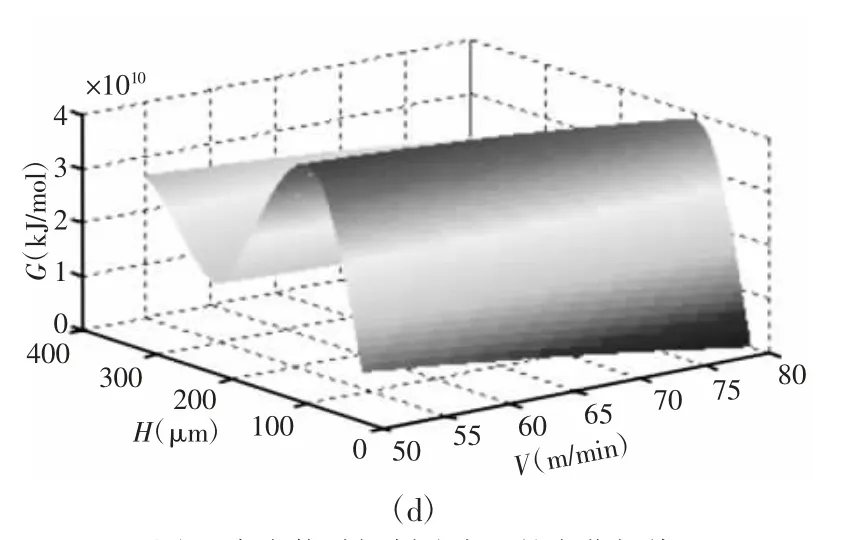
图4 自由能随切削速度ν 的变化规律Fig.4 The Variation Law Between Free Energy and Cutting Speed v

4.2 不同进给量下粘结破损形貌自由能分析

自由能G随进给量f的变化规律，如图5 所示。

图5 自由能随进给量f 的变化规律Fig.5 The Variation Law between Free Energy and Feed f

其中，在切削过程中不同进给量f的自由能G，分析可知，自由能随进给量的增大而增大，粘结破损越严重，如图5（a）所示。不同进给量f和不同粘结面积S下自由能G的三维拟合曲面，由图5（b）可以发现，刀－屑接触区的自由能G随进给量f和粘结破损面积S的变化规律为先递减后递增，有最小值无最大值，且三维拟合曲面呈倾斜L型，如图5（b）所示。不同进给量f和不同粘结体积V下自由能G的三维拟合曲面，由图5（c）研究发现，刀－屑接触区的自由能随进给量f和粘结破损体积V不断增大呈现出先增大后减小的变化，但变化率与图5（b）比较相对平缓，且三维拟合曲面呈U型，自由能有最小值和最大值，如图5（c）所示。不同切削速度ν 和不同粘结破损深度H下自由能G拟合的三维曲面，研究图5（d）可以发现，刀－屑接触区的自由能随切削速度和粘结破损深度的增大呈现先增大后减小的变化，且三维曲面呈弓型，自由能有最小值和最大值，如图5（d）所示。粘结破损面积、粘结破损体积对自由能的影响是先促进后抑制，粘结破损深度的影响与其相反。

4.3 不同背吃刀量下粘结破损形貌自由能分析

自由能G 随背吃刀量ap的变化规律，如图6 所示。其中，在切削过程中不同背吃刀量ap的自由能G，分析可知，自由能G随背吃刀量ap的增大呈现出先减小后增大，如图6（a）所示。不同背吃刀量ap和不同粘结面积S下自由能G的三维拟合曲面，由图6（b）可以发现，刀－屑接触区的自由能G随背吃刀量ap和粘结破损面积S的变化规律为先递减后递增，有最小值无最大值，且三维拟合曲面呈U型，自由能G值最小时的粘结破损面积S为2×106μm2，如图 6（b）所示。不同背吃刀量ap和不同粘结体积V下自由能G的三维拟合曲面，由图6（c）研究发现，刀－屑接触区的自由能G随背吃刀量ap和粘结破损体积V呈正相关，自由能G无最大值和最小值，拟合曲面发散，如图6（c）所示。不同背吃刀量ap和不同粘结破损深度H下自由能G的三维拟合曲面，研究图6（d）可以发现，刀－屑接触区的自由能随着背吃刀量ap和粘结破损深度H不断增大呈现先增大后减小的变化，自由能G最大时的粘结破损深度为70μm，且三维曲面呈S型，自由能G有最大值无最小值，如图6（d）所示。

图6 自由能随背吃刀量ap 的变化规律Fig.6 The Variation Law Between Free Energy and Back Cutting Depth ap

5 结论

（1）以在自由能的角度对硬质合金刀具粘结破损进行研究为目的，在热力学理论的基础上建立了刀－屑接触区的熵变、焓变理论模型，利用所建立的熵变、焓变模型，整合推导出了刀－屑接触区的粘结自由能理论模型。

（2）利用单因素切削实验中获取的粘结破损形貌的相关数据，在自由能的角度对拟合的变化规律图进行分析，得出粘结破损在不同切削参数下的变化情况。结果表明，刀具前刀面接触区具有不同的自由能和粘结破损形貌：自由能随切削速度的增大呈现出先上升后下降的趋势，因此粘结驱动力先增大后减小，接触区表面粘结破损程度较轻；自由能随进给量增大而增大，粘结驱动力随之增大，接触区粘结破损形貌较为严重；自由能随背吃刀量增大呈现先减小后增大的趋势，粘结驱动力先减小后增大，接触区粘结破损最严重。