基于灰关联神经网络的铣削表面粗糙度预测

袁 磊，曾莎莎

（1.海南大学机电工程学院，海南 海口 570228；2.武汉大学动力与机械学院，湖北 武汉 430072）

1 引言

切削是机械制造加工过程中重要的加工方法之一。整个切削加工的过程中，表面粗糙度受到各种加工参数，如主轴转速、进给速度与切削深度的影响[1-2]，同时影响着零件表面的可靠性、耐磨性、疲劳强度、密封性、导热性和传动精度等[3-4]，因此表面粗糙度是评定零件表面粗糙状况、反映零件质量优劣的一项重要指标[5]。

为了达到精确的表面粗糙度常常需要额外的生产成本，许多学者希望利用预测的方式来降低成本，且同时提高产品质量。文献[6]采用回归神经网络发展预测决策系统提高预测表面粗糙度的精确度。文献[7]采用人工神经网络对硬切EN24T 钢表面粗糙度进行预测，回归系数高于0.997。文献[8]采用人工神经网络预测AISI1040 镗削加工表面粗糙度，误差仅有3.47%。文献[9]采用电火花线切割加工航空合金Inconel825 的表面粗糙度预测，平均误差是6.38%。文献[10]采用神经网络预测AA7039 与Al2O3增强复合材料铣削加工的表面粗糙度与切削力，得到的均方根误差分别为2.25%和6.66%。文献[11]采用神经网络预测Ti-6Al-4V ELI alloy 铣削的表面粗糙度，网络的均方误差与相关系数分别为0.002、0.9824，均优于反应曲面法。文献[12]采用神经网络法研究合金钢电火花切削加工中的工艺参数对材料去除率和表面粗糙度的影响。得到总体平均预测误差为0.773%。

在神经网络中需要输入因子才能得到所需的预测值，但是输入因子过多或者是过少皆可能影响到其网络的预测准确性，故在神经网络训练前，先利用灰关联分析，将各因子与预测目标作关联性的排序，并且把不必要的因子剔除，再进行神经网络的训练及预测，经实验证明使用灰关联分析减少因子后，经过神经网络训练可到达理想的预测结果。

2 研究方法

通过灰关联结合神经网络法研究表面粗糙度的预测，在预测系统输入因子前，先筛选输入因子，以提高预测的准确性，其流程图，如图1 所示。

图1 灰关联结合神经网络流程图Fig.1 Flow Chart of Grey Relational Analysis Combined with Neural Network

干扰因子的设定是因为无法得知机床与环境的变化，设定5%为其误差。为了构建预测模型，需首先进行数据的收集。

2.1 灰关联分析

灰关联分析，就是对灰色系统因素间的发展动态进行定量的比较分析。它提供给研究者的信息是：在一个系统中，哪些因素影响较大，哪些因素影响较小；哪些因素对于决策较为重要，哪些因素可以忽略不计。利用灰色系统量化并比较分析，把系统有关因素间的各种关系呈现出来，为系统预测、控制问题提供有用的信息和比较可靠的依据。在灰关联分析中，先对数据进行前处理，也就是灰关联生成。依据数据特性，在此选择越小越好的生成形式，其计算公式为：

式中：xi（k）—灰关联生成后的数值；

maxyi（k）—k个响应中最大值；

minyi（k）—k个响应中最小值。

将各数列正规化之后，即可开始求灰关联系数。首先将每个目标序列与参考序列的差求出，如下所示：

得到两者差序列之后，选取这些差序列中最大差值与最小差值。

分别由式（3）、式（4）表示：

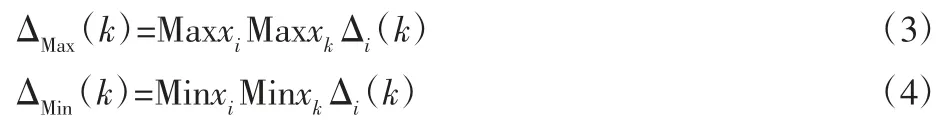
将每个差序列的差值，利用灰关联分析的计算式（5），计算出其灰关联系数，如下表示为：

式中：ψ∈（0，1），i=1，2，3，…n，j=1，2，3，…，m，ξi（k）—灰关联系数；ψ—辨识系数。

辨识系数在灰关联分析中的主要功能是当作参考值与目标值之间的对比，数值的大小可按照实际需求取值。最后将所求的灰关联度依照大小排序，便可知哪些参考数列对于目标序列有着较大的关联度。

在计算平均的灰关联系数时，灰关联度由式（6）计算得到：

2.2 倒传递神经网络

图2 前馈式网络流程图Fig.2 Feedforward Network Flow Chart

人工神经网络（Artificial Neural Network，ANN）是一种基于脑与神经系统研究所启发的信息处理技术，它可以利用一组范例建立系统模型，有了这样的模型便可用于推断、预测、诊断。神经网络发展至今有许多成熟的模型被提出，其中以监督式的倒传递神经网络（Back Propagation，BP）最为普遍。BP 已经被证明最适用于表面粗糙度的问题。倒传递神经网络是多层前馈式网络，其中包含了有输入层、隐藏层以及输出端的输出层，输入层有六个节点，输出层只有一个节点即是表面粗糙度。其构架，如图2 所示。

倒传递神经网络模型的基本原理是利用最陡坡降法的概念，将误差函数最小化。确定目标函数的品质特性是进行下一步分析前的关键，品质特性分为三种：望大，望小，望目。在神经网络中是以均方差（mean-square error，MSE）作为指标，MSE 越低，代表网络预测的效果越好，故选望小特性作为分析工具，均方差与望小特性的信噪比分别由式（7）、式（8）计算得到：

式中：yi—第次的实验值；

n—该项实验的重复测试数或重复实验数。

3 基于灰关联神经网络的表面粗糙度模型的建立及求解

3.1 模型的建立

主要探讨加工参数对表面粗糙度的影响，建立一个基于灰关联结合神经网络的表面粗糙度预测模型。为此选取对应于表面粗糙度变化密切相关的六个因素，分别是刀齿数（A）、每齿进给量（B）、刀具直径（C）、轴向切深（D）、刀具螺旋角（E）、主轴转速（F）作为输入参数，而输出参数为预测表面粗糙度的值（Ra）。各控制因子及水平，如表1 所示。选用田口实验设计法来设计实验，并选取L18 的直交表进行规划。加工材料是铝7075，尺寸为：（150×50×0.8）mm，在工件加工完成后，利用粗糙度仪测量工件的表面粗糙度进行数据搜集。

表1 控制因子及其水平（＊表示初始组合）Tab.1 Control Factor and Its Level（＊Indicates Initial Combination）

3.2 灰关联分析

灰关联分析的过程主要是先进行数据的正规化，然后将各因子与母序列的差计算出来，将序列中最大值与最小值找出后，进行灰关联系数的计算。灰关联分析需要的数据较少，故仅需采集18组实验数据，如表2 所示。数据正规化后开始灰关联分析，如表3 所示。由表3 可知，此研究影响表面粗糙度值最大的因子为刀具直径和轴向切深，此时的最佳参数组合为A1B1C3D2E1F1。初始参数组合下的表面形貌、经田口灰关联后参数组合的表面形貌，如图 3、图 4 所示。

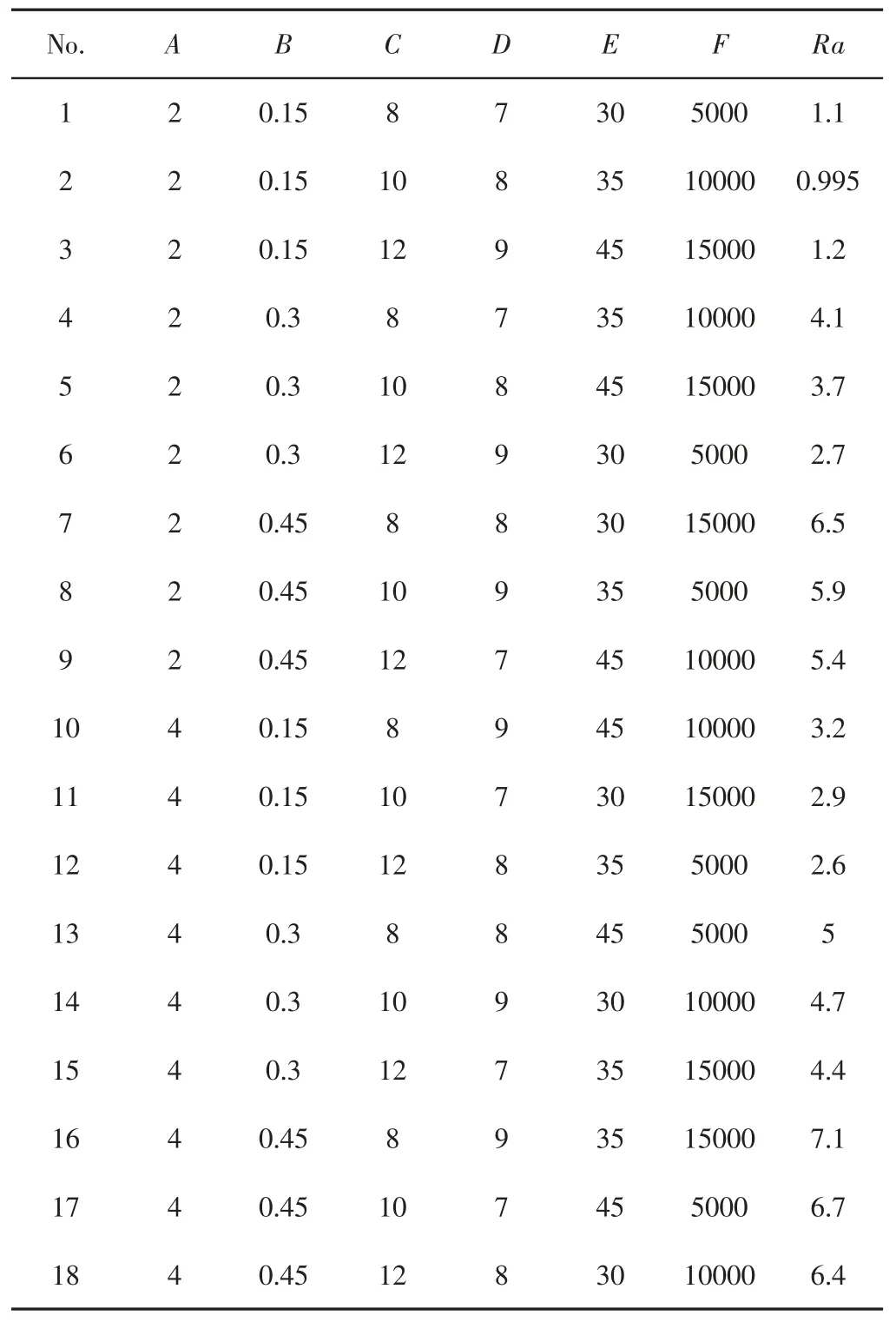
表2 灰关联分析前的原始数据Tab.2 Raw Data Before Grey Relational Analysis

图3 初始参数组合下的表面形貌Fig.3 Surface Topography Under Initial Parameter Combination

图4 田口灰关联参数组合下的表面形貌Fig.4 Surface Topography Under Taguchi Grey Relational Parameter Combination

由图3、图4 可知，经田口灰关联分析后的组合参数得到的表面形貌较初始组合下的表面形貌曲线更加平滑，且表面粗糙度值要小于初始组合下的粗糙度值，证实了田口灰关联分析有效地优化了参数。

3.3 神经网络预测模型的建立与验证

为了使实验数据充足，采用L18（21×35）内直交表配合L18（26）外直交表，整个实验总共有144 组数据。可利用这组数据来训练与测试神经网络，选用MATLAB 中的Neural network toolbox 作为设计与训练神经网络的工具。

选定灰关联神经网络（GRANN）预测模型进行实验，每个部分均进行三次重复实验，并且利用式（8）计算信噪比，最后将神经元个数设定为15 个，而动量系数设定为0.001。动量系数不变，通过调整神经元个数，来进行灰关联神经网络与人工神经网络模型的训练。所得到的结果及其MSE 值，如表4 所示。

表4 两个模型的参数及收敛结果Tab.4 The Parameters and Convergence Results of the Two Models

为了证明模型的准确性，将随机选取的32 组数据放入两个预测系统中作预测，且利用均方根误差（RMSE）作为衡量系统好坏的指标，灰关联分析用于在预测前进行因子的筛选，能有效地提升表面粗糙度预测系统的准确性。

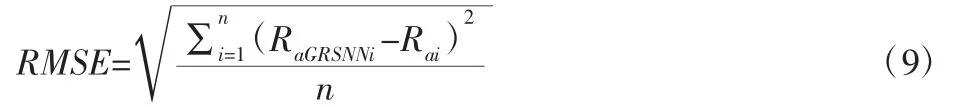
灰关联神经网络预测均方根误差为0.1550，而人工神经网络预测均方根误差为0.0288。由上列的数据可以得知，GRANN预测系统的RMSE 是优于ANN 的，为了增加这里的可信度，故将针对两个预测系统进行假设检验。

3.4 灰关联神经网络与人工神经网络的假设检验

假设检验所使用的数据与前文的数据相同，灰关联神经网络与人工神经网络的假设检验结果，如表5 所示。此假设检验的虚无假设（H0）及对立假设（H1）设定如下：

式中：△μ1—灰关联神经网络预测系统中，预测值与实际值相减取绝对值后的平均；△μ2—人工神经网络预测系统中，预测值与实际值相减取绝对值后的平均；显著水平α=0.05。

表5 灰关联神经网络与人工神经网络的假设检验表Tab.5 Hypothesis Test Table of Grey Relational Neural Network and Artificial Neural Network

由表5 可知，P为0.024 小于所设定的显著水平0.05，故拒绝H0，表示灰关联神经网络预测优于人工神经网络预测，证明所建立灰关联神经网络能有效地预测表面粗糙度。

4 结论

结合灰关联分析与神经网络模型预测了铣削加工的表面粗糙度。首先应用灰关联分析将收集的资料进行分类，再结合神经网络做表面粗糙度的预测，并通过表面粗糙度预测实例验证了所提方法的有效性和正确性。