基于混合法和互补滤波器的车速计算方法
张学科,周优军
(广西科技师范学院,广西 来宾 546199)
1 引言
车速是车辆稳定性控制的关键因素,车速的计算在车辆稳定性控制中占有重要地位。在以往的研究中,根据车速计算模型的不同,车速计算方法可分为运动学方法和动力学方法。在车辆速度的运动学计算方法中,常用的方法是轮速法和直接积分法。国内外许多学者在此基础上进行了大量的研究。
参考文献[1]使用非线性滤波观测器计算配备有ABS 的车辆速度,但其实质仍然是最大轮速法和自适应斜率法的综合应用。文献[2-4]采用基于车轮速度法和直接积分法的卡尔曼滤波计算方法对车辆的纵向速度进行计算。文献[5]基于ABS 的控制状态,提出了一种结合车轮速度的纵向速度计算方法。文献[6-7]对传统的最大轮速法、坡度法和综合法进行了分析,提出了计算纵向速度的递推法,并与最大轮速法和雷达测速法进行了比较,以修正计算的车辆速度。文献[8]利用车轮速度信号和车体加速度信号,考虑到制动过程中车轮半径的变化和加速度传感器的偏移误差,采用递推最小二乘算法实现对车速的实时计算。在动力学计算方面,一般是通过车辆的轮胎力计算和轮胎动力学模型来实时计算车速。在文献[9]中,根据车辆动力学模型和轮胎模型,并采用非线性计算法来计算车速。文献[10]利用了分布式电动汽车驱动力矩和制动力矩容易计算的优点,采用轮胎动力学模型来计算车轮的纵向力,从而得到车速的计算值。
综上所述,基于运动学的计算方法具有较好的鲁棒性,计算结果基本上不受模型参数的影响,但其精度取决于传感器信号的质量。而基于动力学的计算方法鲁棒性较差,其结果依赖于模型参数的可靠性,但对传感器的要求不高。因此,如何基于车辆的纵向响应特性,综合考虑两类计算方法的优势,实现对车辆速度的协同计算,进一步提高计算的精度,并兼顾实时性,还有待进一步的探讨。
为此,在分析汽车纵向运动特性的基础上,提出了一种车速的混合计算法,它综合了运动学方法和动力学方法的优点,同时为了提高ABS 工作时自适应滤波器计算的稳定性,设计了相应的扩展滤波器。最后通过CarSim/Simulink 联合仿真平台验证了所设计系统的有效性。
2 动力学建模
2.1 车轮转动动力学模型
为了计算轮胎纵向力,采用的轮胎动力学模型,如图1 所示。车轮转动动力学方程为:

式中:ω—车轮角速度;Re—车轮有效半径;Iω—车轮转动惯量;Tm/Tb—驱动/制动力矩;Mμ—滚动阻力力矩;Fx—纵向轮胎力。
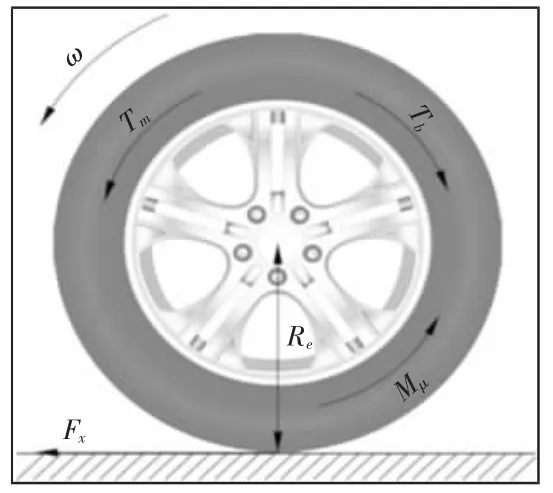
图1 轮胎转动动力学模型Fig.1 Tire Rotation Dynamics Model
2.2 Dugoff 轮胎模型
根据Dugoff 轮胎模型,轮胎纵向滑移率定义为[11]:

式中:Vω—车轮的纵向速度;V—车辆的纵向速度。
基于Dugoff 轮胎模型,轮胎纵向力可以表示为:

变量H和λ(H)表示如下:

式中:Cx、Cy—轮胎纵向刚度和横向刚度;α—轮胎侧偏角;μ—路面摩擦系数;Fz—车轮受到的垂直力。
3 车速计算器设计
该计算器的设计主要分为两个方面:车辆基本速度算法的设计和紧急制动时ABS 对速度计算的补偿增益。
3.1 混合计算方法
根据车辆运动学特性,有以下表达式[12]:

式中:—车辆纵向速度计算值;ax—纵向加速度;Vω—轮胎与地面接触处的线速度;K—计算器的反馈增益。
根据式(4)可以求出车轮速度Vˆω的计算值,表示为如下:

基于Dugoff 纵向力模型,轮胎纵向滑移率可以表示为:

根据式(1)计算得到轮胎纵向力为:

为了防止单轮滑移时对车速计算产生较大影响,每个车轮的滑移率大小决定比例反馈中车轮速度误差的大小。故进行如下设置:

式中:下标L1、L2、R1、R2—前左轮、左后轮、右前轮和右后轮。
因此,最终轮速误差定义为:

所提出的计算方法的结构,如图2 所示。
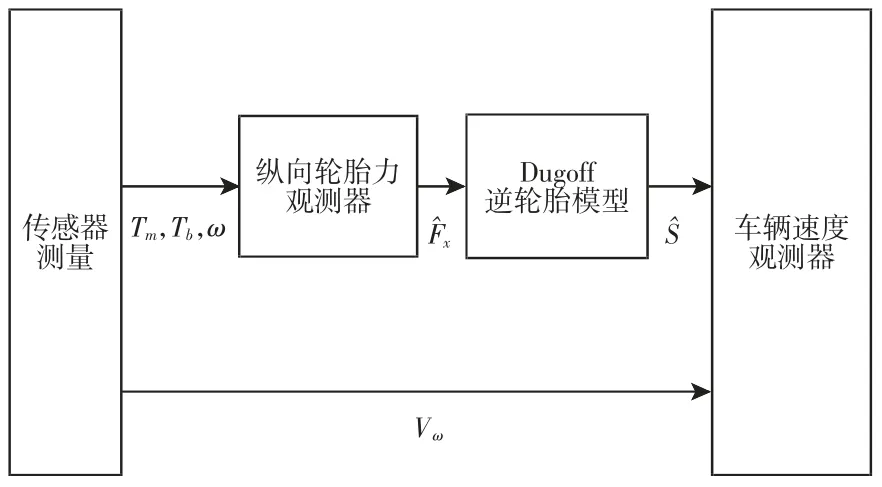
图2 车速计算策略Fig.2 Speed Calculation Strategy
3.2 扩展计算器的设计
在紧急制动过程中,车辆上的ABS 开始起作用,以保证制动性能。当车轮即将到达下一个锁止点时,制动油的压力使气囊不断重复动作,使其在一秒钟内可以动作(60~120)次,相当于不断的停止和放松,因此,防抱死制动系统可以避免紧急制动时方向失控和车轮侧滑,使车轮在制动时不抱死,从而增加摩擦和制动性能,保证车辆制动时的安全。
ABS 每秒可作用(60~120)次,因此车轮转速会以相同的频率升降。由于上述算法不处理信号的频率,在紧急制动时,车速计算器会利用轮速信号将波动带入车速的计算中,其波动的影响,如图8 所示。
当使用上述算法来计算车速时,虽然结果包含了ABS 作用下车轮的波动,但总的车速计算趋势仍然较为准确。因此,混合计算的结果可以反映出车辆速度的稳态特性[13]。为了进一步提高计算器的性能,利用互补滤波器设计扩展计算系统,如式(11)所示。

由于互补结构中的两个低通滤波器具有相同的截止频率,这意味着低通滤波器和高通滤波器是互补的。在这种情况下,扩展计算器可以从上述方法的结果中过滤高频信息,并融合纵向加速度携带的高频信息,从而得到更准确的车速计算值。扩展计算值的设计方案,如图3 所示。

图3 扩展车速计算方法Fig.3 Expands the Speed Calculation Method
4 仿真结果及其分析
基于CarSim-Simulink 联合仿真平台与传统的最大轮速法进行对比分析,验证了所提出的车速计算方法的有效性。
在仿真中,将车辆设置为四轮独立驱动的电动汽车。主要参数,如表1 所示。
仿真测试场景选择为加速后制动和双车道变换两种情况,并分别在高附着路面(μ=0.85)和低附着路面(μ=0.35)进行仿真,以验证混合计算法的有效性。最后通过紧急制动工况仿真测试来验证扩展计算器的计算性能。

表1 车辆参数Tab.1 Vehicle Parameters
为便于分析结果,将绝对误差定义为:

相对误差定义为:

式中:ε—绝对误差;ρ—相对误差;V—车速的真实值;—车速的计算值。
4.1 加速后制动工况测试
该仿真测试工况是在直线行驶条件下,分别在高附着路面(μ=0.85)和低附着路面(μ=0.35)进行仿真,程序设定为从0km/h 加速到120km/h 的速度,然后在3.5MPa 制动总泵压力下施加制动。
高附着路面(μ=0.85)和低附着路面(μ=0.35)混合计算器的计算结果,并将其与最大轮速法和车速的参考值进行了对比,如图 4、图 5 所示。

图4 高附着路面的对比结果Fig.4 Comparison Results of High Adhesion Road Surface
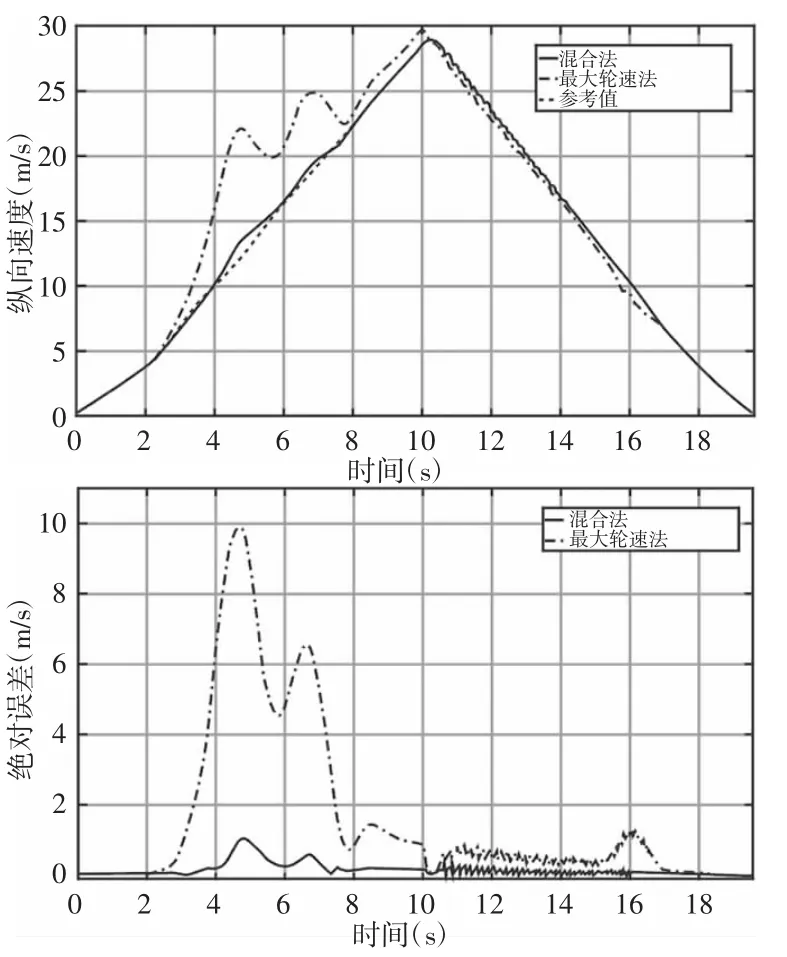
图5 低附着路面的对比结果Fig.5 Comparison Results of Low-Adhesion Road Surface
在高附着路面(μ=0.85)上,最大轮速法的最大绝对误差和相对误差分别为0.42m/s 和2.25%,而混合计算器的结果为0.3m/s和1.25%。在低附着路面(μ=0.35)上,最大轮速法表现很差,其最大绝对误差和相对误差分别为10m/s 和84.1%,而混合计算器的最大绝对误差和相对误差分别为1.2m/s 和8.1%,表明所提出的算法在直线行驶工况下具有较高的精度。
4.2 双车道变换工况测试
为了验证车辆有横向移动时混合计算器的性能,进行双车道变换测试仿真。设定车辆以120km/h 的车速分别在高附着路面(μ=0.85)和低附着路面(μ=0.35)行驶,不进行加速和制动操作。
混合计算法、最大轮速法以及参考值之间的比较结果,如图6、图7 所示。当车辆横向运动时,由轮胎的摩擦圆曲线可知轮胎的横向和纵向特性相互影响。当轮胎横向力过大时,轮胎的纵向特性可能进入非线性区域。因此,引入了Dugoff 模型来减弱轮胎非线性对车速计算的影响。
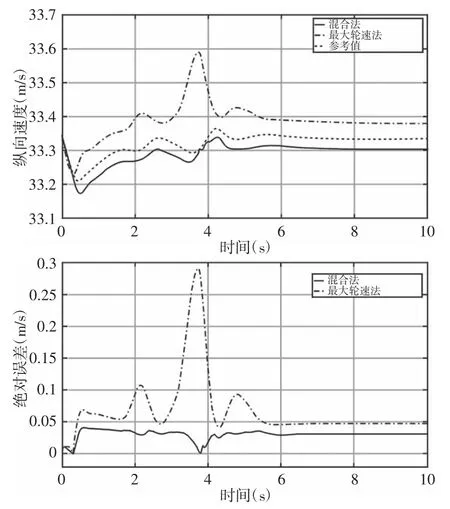
图6 高附着路面的比较Fig.6 Comparison of High Adhesion Road Surface

图7 低附着路面的比较Fig.7 Comparison of Low-adhesion Road Surface
在高附着路面(μ=0.85)上,最大轮速法的最大绝对误差和相对误差分别为0.29m/s 和0.9%,而混合计算器的结果为0.04m/s和0.16%。在低附着路面(μ=0.35)上,最大轮速法的最大绝对误差和相对误差分别为0.68m/s 和2.1%,而混合计算器的最大绝对误差和相对误差分别为0.14m/s 和0.43%,表明所提出的算法在车辆有横向移动时仍具有较高的精度。
4.3 加速后制动(开启ABS)工况测试
该仿真工况设置为车辆在路面附着系数为0.85 的路面直线行驶,从0km/h 加速到120km/h 后,在10MPa 制动总泵压力下施加制动,制动期间ABS 被激活。
混合计算器和最大轮速法的计算结果,这两种方法在加速时表现很好,但在减速时有振荡发生,如图8 所示。当ABS 处于工作状态,由于ABS 的控制算法多为逻辑阈值法,所以在紧急制动过程中,车轮转速以波动信号出现,直接影响了两种方法的效果。但混合计算器引入了Dugoff 轮胎模型,使该计算器的结果能够包含高频波动。因此,它可以提供进一步修正计算结果的可能性。

图8 加速后制动开启ABS 时高附着路面的比较Fig.8 Comparison of High Adhesion Road Surface when ABS is Opened by Braking After Acceleration
4.4 扩展计算器仿真
为了验证扩展计算器的有效性,进行加速后制动工况仿真测试。在此仿真工况下,扩展计算器明显抑制了最终结果的波动,如图9 所示。为了进一步证明扩展计算器的优越性,将该方案与最大轮速法进行了比较。由图9 可知,最大轮速法的最大绝对误差可达3.3m/s,相对误差可达15%,而改进的计算方法最大绝对误差不超过0.5m/s,相对误差为2%。
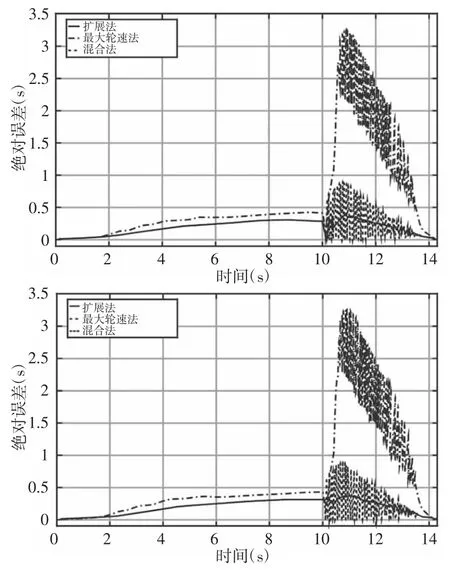
图9 三种算法的比较Fig.9 Comparison of the Three Algorithms
5 结论
基于车辆的纵向运动特性,采用混合计算方法,提出了一种实时计算车辆纵向速度的算法。针对ABS 工作时车速计算误差较大的问题,进一步利用互补滤波器对计算结果进行修正,改进了算法的精确度。设计车速计算系统,并通过CarSim/Simulink 联合仿真平台验证了系统性能,得出如下结论。
(1)所提出的纵向车速计算方法,通过综合考虑车辆运动学和动力学特性,实现了对车速的精确计算。仿真结果表明,算法在多种工况下都有较好的性能。
(2)基于互补滤波原理的车速扩展计算方法,能够通过对初次计算值的修正,提升计算精度,在兼顾准确性的同时,消除了ABS 工作时的波动干扰,这将为进一步将该车速计算值应用于车辆稳定性控制系统提供参考。

