夸克胶子等离子体的电导:色流体力学方法
蒋冰峰
(湖北民族大学 信息工程学院,湖北 恩施 445000)
通过相对论重离子碰撞可以产生退禁闭、自由状态的夸克和胶子——夸克胶子等离子体(Quark Gluon Plasma,QGP).实验结果显示相对论重离子对撞机(RHIC)和大型强子对撞机(LHC)上产生的热夸克胶子流体具有粘滞性.输运系数,如切向粘滞、体粘滞、热导、扩散系数以及电导显著地影响着重离子碰撞后产生的QGP的演化过程[1-2].
夸克是构成物质的基本粒子,既带色荷,又带电荷,电导体现着QGP系统对电磁扰动的响应,反映着系统的电荷弛豫规律.在QGP中,电导是其演化方程中的一个非常重要的物理量,它决定着系统中的能量-动量演化和系统的夸克-胶子化学平衡[3].在非对心重离子碰撞中,电导决定着产生的瞬变磁场的强度和寿命,因而影响着手征磁效应的强度[4-6].另外,电导也显著地影响着重离子碰撞中软光子和低质量双轻子的产生[7].
近年来,人们分别在QGP动理论[8-9]、玻尔兹曼方程数值解法[10-11]、准粒子模型[12]、戴森-许温格方程[13]、强磁场环境[14-15]和格点规范理论[16]等理论框架下讨论研究QGP的电导.流体力学方法在模拟描述相对论重离子碰撞后产生物质的椭圆流、粒子横动量谱等方面取得重要的成功.用流体力学理论框架讨论QGP的电磁性质目前还不多见[17-18],还有待进一步扩展深入.本文将在色流体力学的理论框架下研究QGP的电导.
1 电导:色流体力学
可以用协变形式的欧姆定律来求解QGP的电导[8-9]:
(1)
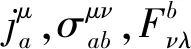
协变形式的四流方程和能量动量守恒方程为[17-20]:
Dμnμ=0,
(2)
(3)
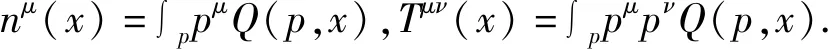
(4)
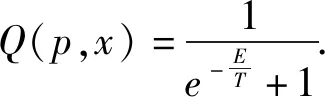
nμ=n(x)uμ,
(5)
(6)
(7)
方程(1)、(2)、(3)和(7)构成了理想色流体力学的基本方程.
流体力学量n,uμ,ε和p通常情况下分成无色和有色两部分,如粒子数密度可以写成如下形式:
(8)
其中色指数α,β=1,2,3;I是单位矩阵.
(9)
(10)

(11)
(12)
(13)
(14)
(15)
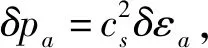
(16)
(17)
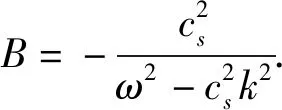
根据方程(7),流体力学量的色涨落激发的色流表示为:
(18)

(19)
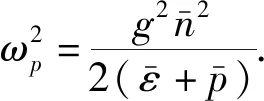
根据式(1),电导张量可表示为:
(20)
(21)

(22)
(23)
(24)
(25)
(26)
其中ξ是无穷小量.从式(26)可知,σT/ωp是纯虚数,因此,在理想色流体力学方法下,QGP的电导主要由纵向电导决定.
2 结果与讨论
色流体力学方程组(1),(2),(3)和(7)是从无碰撞项的QGP动理论方程推导而来,因此电导(25)(26)相应于硬热圈近似水平的结果.为了更详细地研究QGP的电导性质,论文在T=ωp,k=0.2ωp的情况下研究讨论标度纵向电导σL/ωp的实部与虚部随频率ω的变化关系.
图1计算了纵向电导实部ReσL/ωp随频率变化关系.从图1中可以看出,在类空区间ω
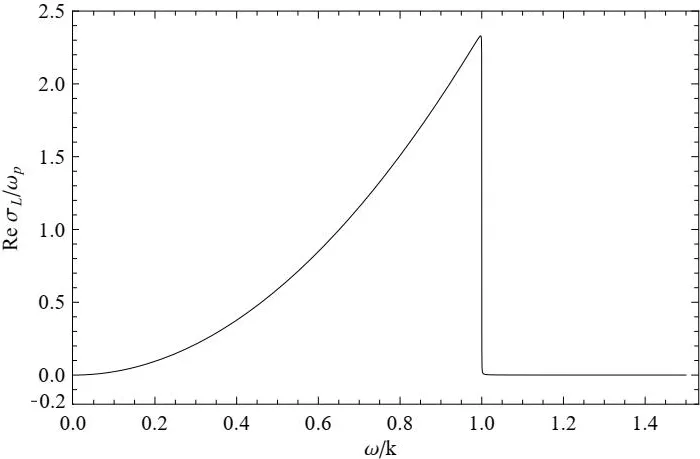
图1 标度纵向电导实部随频率的变化关系曲线Fig.1 The real part of the scaled longitudinal electric conductivity ReσL/ωp as a function of frequency ω
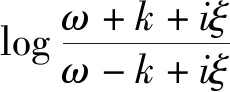
(27)
Θ为阶梯函数,当ω
图2计算了纵向电导虚部ImσL/ωp随频率变化关系.在类空区间ω 图2 标度纵向电导虚部随频率的变化关系曲线Fig.2 The real part of the scaled longitudinal electric conductivity In σL/ωpas a function of frequency ω 在极端相对论重离子碰撞中,在产生的高温高压下,强子物质将会发生退禁闭相变形成夸克胶子等离子体.夸克既带电荷又带色荷,在外场下或电磁扰动的情况下夸克胶子等离子体中将存在电荷弛豫现象,电导决定着等离子体介质的电磁响应过程.在理想色流体力学的理论框架下本文计算了夸克胶子等离子体的电导,得到的结果相应于硬热圈近似的结果.在此理论框架下得到的横向电导是纯虚数,电导的性质主要由纵向部分体现.标度纵向电导实部在类空区间随着频率的增大而增大,但在类时区间其结果等于零.标度纵向电导的虚部在类空区间先减小,然后快速随频率增大.在类时区间,虚部单调减小.电导这些有趣的性质有可能为重离子观察量带来可观察的效应,这是未来值得进一步研究的课题.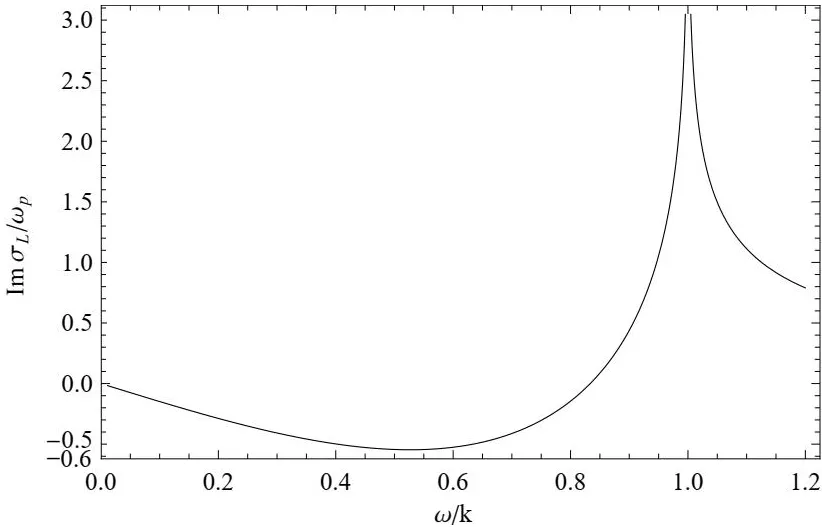
3 结论

