大型自由曲面光学器件的超精密抛光方法*

周 波，李 论，田同同，赵吉宾

（1.中国科学院沈阳自动化研究所，沈阳 110016；2.中国科学院机器人与智能制造创新研究院，沈阳 110169）

目前，球形和非球形光学系统的应用越来越受到成像性能以及现代光学系统的高质量要求的挑战，而由自由曲面表达的复杂光学表面是解决此问题的关键[1]。光学自由曲面通常是指不可展的复杂光学表面，它可以具有任意规则或不规则的表面结构[2]。与传统的光学部件相比，它具有不对称的结构并具有灵活的空间布局。经优化设计扩展的自由度，显著提高了光学系统的视场适应性，并使光学系统可以获得更大的成像视场，改善了其光学性能，并简化了系统结构，可减少镜片的数量以及镜片的尺寸[3]。因此，基于自由曲面的光学系统研究已成为发展新一代高性能光学系统的重要方向。

高轮廓精度的自由曲面的应用，使得大视场、高分辨率反射长焦系统的设计日益成为欧美发达国家的关注焦点，并在自由曲面研究领域取得了突破。NASA 已使用的自由曲面的红外光谱成像仪也采用了自由形式的表面[4]。国际知名的光学系统制造商徕卡（Leica）为欧洲航天局（ESA）开发了一种新型的自由曲面光学表面[5]。TMA 相机也使用自由曲面，并且全场波像差的RMS 值从λ/ 7 提高到λ/ 20[6]。

大口径自由形状零件的高端加工技术和设备被以美国为首的西方国家视为战略资源，并严格限制了出口。由于其特殊的几何结构和材料特性，对打磨的路径规划技术的要求非常高。综上所述，以自由曲面表示的复杂光学表面在重要的光学工程、国防军事等先进领域具有广阔的应用前景，将成为光学系统技术发展的主要方向。为解决现有自由曲面光学器件表面加工的关键问题，开发了用于大直径自由曲面零件的智能、高精度、高效超高精度机器人抛光加工平台。

传统的数控轨迹生成方法，如等距轮廓偏置、螺旋轨迹以及往复路径等，均需要避免路径交叉并追求更高的效率以实现高速加工。但是，抛光路径为了防止单一方向运行导致的中频、高频误差，其方向需要不断变化，以有效地消除抛光纹理。现在的抛光路径除了前述的传统方法，还有基于分形算法的谢尔宾斯基曲线或者希尔伯特曲线，但是其生成路径有规律可循，一定程度上仍无法做到消除中频及高频误差。基于此，本文提出下述抛光轨迹算法，具体见图1的算法流程图。

图1 算法流程图Fig.1 Flow chart of algorithm

自由曲面的不规则形状特性为光学系统赋予了新的活力，但同时也为其制造技术带来了巨大挑战。依赖于手动和简单机械的传统加工方法属于质量不稳定的研磨和抛光技术，无论精度或加工效率，都无法满足复杂曲面的加工要求。

随着机器人技术的日益成熟及其具有的更大加工灵活性以及加工范围，可以使用六轴工业机器人夹持抛光工具进行抛光操作，其更具有成本低廉的特性，但由于工业机器人的低刚性（约0.1mm）而降低了其定位精度[7]。很多研究人员使用CNC 机床进行此类精加工阶段。Lin 等[8-9]设计和开发了一种五轴CNC 柔性砂布轮抛光机床，并研究了其抛光工艺[10]，柔性抛光有效地改善了表面质量，而又不影响工件的深层质量。Tsai 和Huang[11]设计了一种特殊的五轴机床进行抛光操作。

计算机控制的光学抛光（Computer control optics surface，CCOS）技术[12]，特别是一些新颖的抛光技术，如应力板抛光、磁流变抛光、离子束抛光和球囊抛光等确定性抛光技术的创新，促进了光学元件的革命性高精度制造。但是，当将上述商用抛光技术应用于大直径光学自由曲面的高精度加工时，存在一个明显的问题：自由曲面元件不同于球形表面和简单的非球形元件，并具有一定的边界功能。目前，商业数字抛光技术加工坐标系无法实现复杂曲面光学元件的识别和精密加工。同时，因数控机床的加工范围有限及其不具有机器人的加工灵活性，这些新颖的抛光技术绝大多数采用了机器人平台进行抛光。

本研究克服了现有技术的局限性，并提出基于旅行商问题生成无交叉路径的抛光方法。

边界参数化

对曲面进行参数化就等于找到从合适的域到曲面的一对一映射。对表面网格进行参数化的目的是找到从平面网格到三角网格曲面的一对一映射规则。一个好的映射规则需要符合角度变形（共形参数化）或面积变形（保面积参数化）最小化的规则。根据所需的边界参数化类型，可以将不同的参数化方法分为3类：固定边界、自由边界和无边界[13]。本文采用前两种边界法。

1 分层切片算法

固定边界表面参数化法是定义一组约束边界参数化的方法，即沿边界的每个顶点由两个u、v坐标[13]来定义。为固定边界方法选择边界参数化方案时，提供两种不同的选择：

（1）用户可以在两种常用方法中选择边界参数化：均匀或弧长参数化。均匀即等距划分的边界参数化虽然会产生较差的视觉效果，但更稳定。为了更符合减小加工误差的原则，在默认情况下，使用弧长边框参数化的方法。

（2）由两个标准形状中的一个形状来代表平面域的边界形状：圆形或正方形。正方形边界参数化通常用于近似矩形。圆形边界参数化对应于近似于圆形的投影。

相对于固定边界表面参数化法，自由边界表面参数化法保证更好的映射精度[14-16]，但是映射域的边界复杂，加大了规划路径的难度。传统的往复路径(即Zig-Zag)或等距轮廓偏置（即CPO）因路径生成简单，可以适用于自由边界映射域的路径规划。而前述的谢尔宾斯基曲线或者希尔伯特曲线，则不适用于自由边界映射域，因两者均在圆域或方域内方便进行分形计算，在自由边界域内规划非常困难。本文采用的通过在映射域内生成随机点的方法，突破了上述路径因映射精度及路径规划难度等问题，可以在圆域、方域及自由边界映射域内生成无交叉路径，完成了抛光路径的生成。

针对上述平面域的选择问题，通过将曲面网格投影到平面上，可以获得区域轮廓，根据计算圆形度的数值来判断形状并选择边界参数化类型，如图2所示。

图2 网格曲面适用类型Fig.2 Applicable types of mesh surfaces

圆形度的计算公式如下：

式中，Circularity为圆形度；Area为投影区域的轮廓包围面积；Length为投影区域的轮廓长度。当投影区域的圆形度接近1（本文选择为超过0.9），则适用于选择圆域；当投影区域的圆形度值相对小（考虑到方形域为0.785，本文选择为介于0.8 与0.9之间），则适用于选择方域；当圆形度值小于0.8，则选择自由边界映射域。

2 重心坐标系

参考2D 广义重心坐标[17]的定义，其提供了为二维三角形定义的广义重心坐标的高效的实现方法。为了方便地产生抛光轨迹，必须将映射平面内三角形的坐标以重心坐标系的形式表达，再将该坐标映射到三维网格曲面上，从而方便地获得最终的抛光轨迹，如图3、4所示。

图3 天狗面具的映射平面域Fig.3 Mapping plane of tengu mask

图4 Emijo 面具的映射平面域Fig.4 Mapping plane of Emijo mask

点q的三角形上的任何点都可以表示为式（2），见图5。

可以将q表示为三角形顶点的加权平均值。如前文所述，平面域的索引遵循一对一的映射规则，并且与原始曲面网格相同，点q对应于原始曲面网格的平面域上面片内的一个点坐标，其坐标可以通过式（2）计算。

图5 平面网格面片上的重心坐标Fig.5 Gravity coordinate on patch

轨迹规划

传统的抛光路径方法包括：往复、等距轮廓偏置、螺旋形、希尔伯特（Hilbert）填充曲线[18]、均匀有理B样条曲线（NURBS）曲线拟合[19]等。为了防止单一方向运行导致的中频、高频误差，并消除抛光纹理，抛光路径方向需要不断变化。相对于有规律可循的基于分形算法的谢尔宾斯基（Sierpinski）曲线[20]或者希尔伯特曲线的抛光路径，无规律的随机路径更适用于消除中频、高频误差，但是需要采用一种高效的且可以将随机点用“一笔画”的方式进行连接，以生成无交叉的高效随机路径。

旅行商问题（Travelling salesman problem,TSP）是计算数学中研究最深入的问题之一。给定一个城市的集合以及每对城市之间的旅行成本，那就是找到访问所有城市并返回起点的最经济的方法[21]。对于抛光轨迹，可以在平面网格中生成随机点，并通过TSP 方法进行连接，从而可以使抛光轨迹最短。

但是TSP 问题尚无有效的解决方法[22]，任何方法均不能保证其获得的是最短的路径，只有相对短和高效的算法。在这些求解方法中，加拿大Uwaterloo 大学的研究人员[23]提出的算法和基于Lin-Kernighan的本地搜索算法[24]求解TSP 都非常节省时间并保证结果是相对优良的。随着点数的增加，各个计算方法的时间消耗将急剧增加。比较随机点（2000个点）的时间消耗和准确性的计算结果，如表1所示。

可见，基于Lin-Kernighan算法求解TSP的算法具有良好的时间消耗和准确性。虽然路径长度略大于Uwaterloo 大学的计算结果，但是计算效率的优势非常明显。相对于缩短冗长的打磨抛光路径长度的难度，计算效率的提高更具有实际意义，这样才能实现算法较高的“质速比”。

1 蚁群算法

本文采用蚁群算法来提高计算速度。蚁群算法是一种用来寻找优化路径的概率型算法，1992年由Dorigo[25]在其博士论文中提出，其灵感来源于蚂蚁在寻找食物过程中发现路径的行为。这种算法具有分布计算、信息正反馈和启发式搜索的特征，本质上是进化算法中的一种启发式全局优化算法[26]。本文采用蚁群算法解决前述的以TSP 求解路径连接问题，算法的流程如下（以某一只蚂蚁的行走路径代表一个可行解，即一个路径连接方案）：

（1）设定迭代次数。

（2）确定蚂蚁数n。

①对每只蚂蚁，随机选择一个抽象点作为起点；

·进入循环选择后n-1个抽象点；

·根据所有与当前抽象点相连的路径上的信息素多少，决定下一步，即选择信息素最多的路径；

·蚂蚁有一定概率选择错误，即随机选择下一步要走的路径；

·在选择的路径上按照一定规则留下一定量的信息素；

②蚂蚁行走路径就是本次搜索的轨迹连接路径；

（3）每群蚂蚁结束后，所有路径上的信息素进行一次衰退，保证越后进行的蚂蚁的信息素影响越大。

（4）等待迭代结束。

设定更新选择的路径上的信息素方式为式（3），其中u为信息素衰退因子；Q为常数因子；len为从起始城市回到城市的路径距离。

并设定全局更新信息素为蚁密系统。

2 TSP算法对比分析

将几种TSP算法运行对比，以验证所提出算法的有效性，轨迹连接效果和统计数据分别见图6及表2。

从表2可以看出：（1）除Uwaterloo大学及本文所提出的算法，其余算法都存在交叉；（2）虽然Uwaterloo 大学所提出的算法路径最短，但是计算时间显著较长，其算法的时空效果并不好。与连接路径的长度相比，本文方法在时间消耗方面表现出更好的性能。因此本文推荐使用蚁群算法计算TSP。

表1 仿真结果统计Table1 Statistics of simulation results

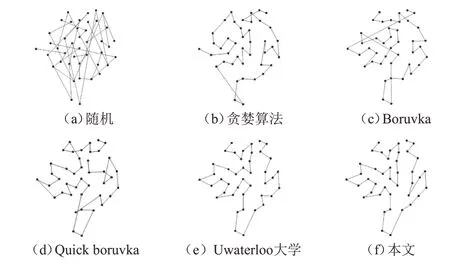
图6 多种连接方法对比Fig.6 Comparison results between multiple connection methods

3 TSP 随机点预设置数量

曲面模型的表面积可以通过累计每个面片计算，

式中，i是每个面片的索引，且bi是第i个面片的面积。设打磨工具的有效投影面积为s。则TSP 随机点预设数量n为：

考虑到三角网格曲面模型的复杂程度不同，本文逐次适当放大随机点数以保证不残留加工区域以及不过度加工，则放大的随机点数数量n′= (1.05～1.1)m×n。其中，m是逐次放大随机点数目的次数。

尤其需要注意的是，在自由边界平面域内生成随机点的数量不同于圆域及方域。因自由边界平面域外轮廓复杂，首先需要在单位方域内进行随机点的生成，再判断这些点落在自由边界平面域的情况，进行随机点的补充。本文是以方域的面积与自由边界域的面积相比，适当放大随机点生成的数量，以保证有足够的数量落在自由边界域内。

数值模拟及抛光试验验证

为了评估所提出的TSP 轨迹规划算法，图2中所示的两个网格曲面被用作工作示例：“天狗面具”和“Emijo 面具”网格曲面，都包含多个小面片。前者包含4000多个三角面片，后者的网格构成了600多个切面。通过前述参考加工参数，分别确定TSP 点的预设数量。如果预设的TSP 点数少（实际上不能覆盖表面网格），则TSP 点数会增加，同时也会影响加工效率。因此，在合理的限制范围内考虑加工精度和耗时，本文中的TSP 数量将设置为1174 和464。统计数据如表3所示。

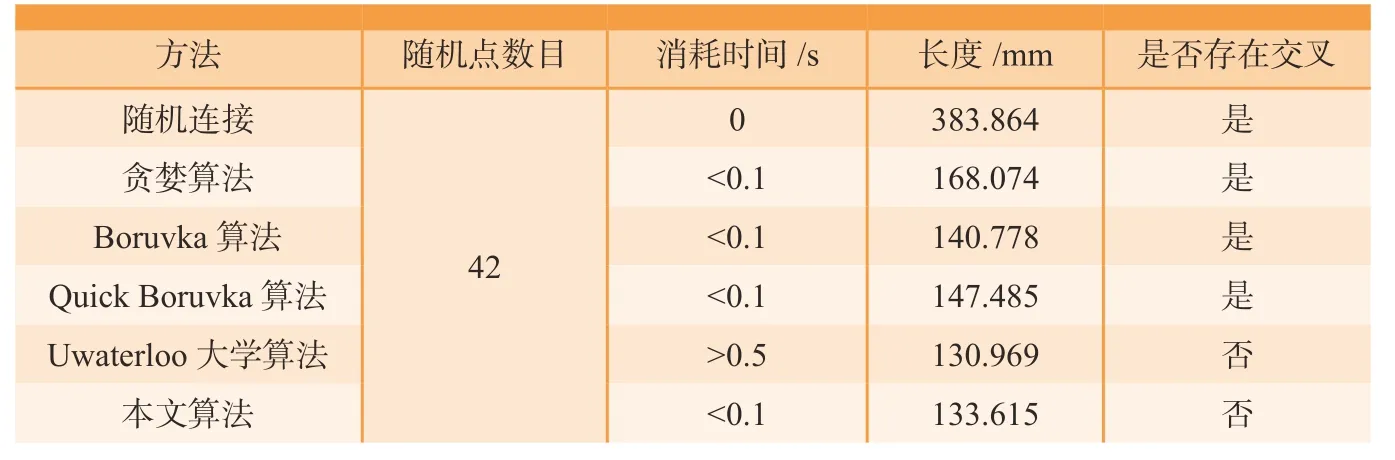
表2 TSP 轨迹生成时间统计Table2 Statistics of TSP trajectory generation time-consuming

表3 计算数据统计Table3 Statistics of TSP calculation results

1 仿真模拟

1.1 “天狗面具”实例

在图7中所示的“天狗面具”的平面网格内随机分布1174个随机点。

图8示出了根据重心坐标对应获得的抛光工具路径。

该模型的投影域圆形度为0.813，所以适用于采用方域作为映射域进行计算。从图8中也可以得出，方域映射后获得的抛光路径的边界覆盖情况比圆域的情况要理想；圆域映射后在模型的边界处出现多处路径没有覆盖到的情况。因此，采用方域进行映射是合理的。

图7 天狗面具平面域内TSP 路径Fig.7 TSP path in plane domain of Tengu mask

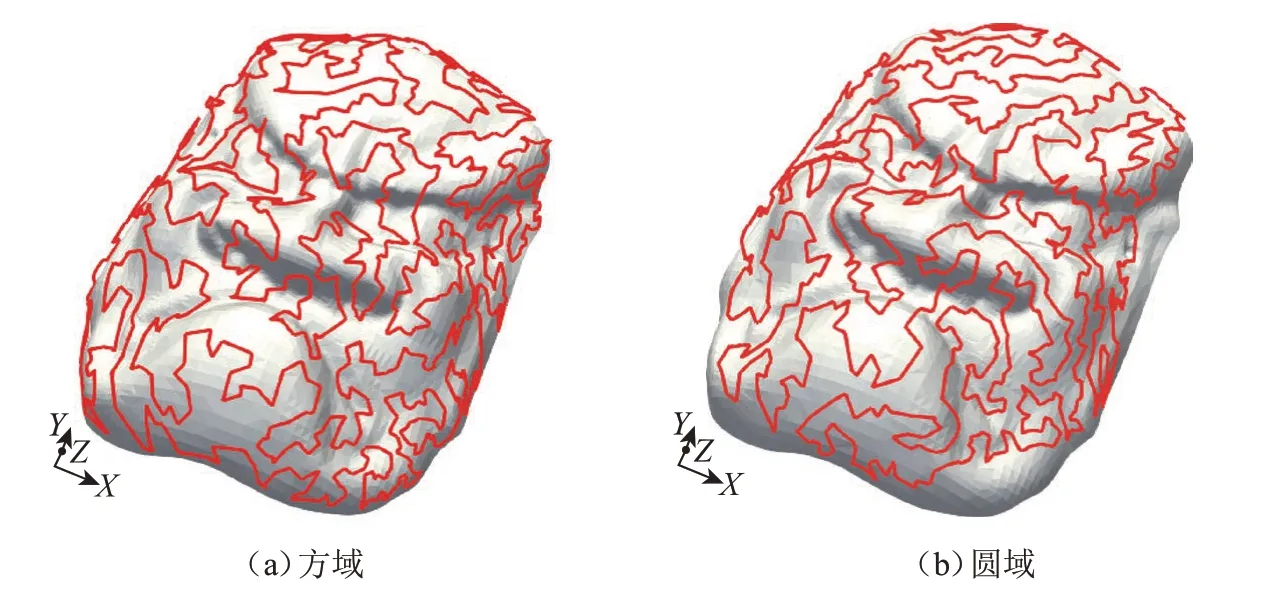
图8 天狗面具TSP 抛光路径Fig.8 TSP polishing path of Tengu mask

1.2 “Emijo 面具”实例

在图9中所示的“Emijo 面具”的平面网格内随机分布464个随机点。

图10示出了根据重心坐标对应获得的抛光工具路径。

该模型的投影域圆形度为0.925，所以适用于采用圆域作为映射域进行计算。从图10中也可以得出，圆映射后获得的抛光路径的边界覆盖情况比方域的情况要理想；而方域映射后在模型的边界处出现多处路径没有覆盖到的情况。因此，采用方域进行映射是合理的。

2 抛光试验

本文通过试验对比所提出的TSP 路径规划方法与基于谢尔宾斯基轨迹的抛光轨迹规划方案的打磨效果。因所选择的模型（原件为某自由曲面，材料为光学玻璃）具有较大的坡度且部分区域具有尖锐的几何特征，投影后的圆形度数值仅为0.602，显然采用圆域和方域并不适合进行路径规划。此外，采用谢尔宾斯基路径，阶数及等分的数量（圆域）将直接影响生成效率，本文给出生成近似数量（2700）的点所消耗的时间，并在图11中的平面域内规划谢尔宾斯基路径（阶数为7），在表4统计生成点位及计算时间，可见所提出的算法在时间消耗方面具有优势。

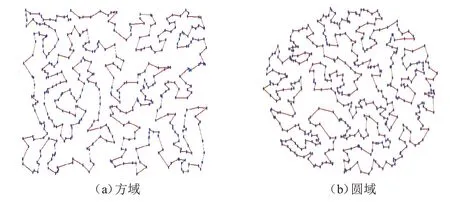
图9 Emijo 面具平面域内TSP 路径Fig.9 TSP path in plane domain of Emijo mask

图10 Emijo 面具TSP 抛光路径Fig.10 TSP polishing path of Emijo mask

图11 谢尔宾斯基平面域内路径（4 阶）Fig.11 Sierpinski polishing path of Emijo mask

试验装置采用KUKA 机器人(吊装方式安装)，额定负载30kg，末端装置自制打磨盘(配1200#砂纸)进行抛光试验，抛光压力均为5N；抛光盘半径为48.0mm，如图12所示。（1）采用谢尔宾斯基路径：在圆域生成路径（阶数为9，大致为7200个点），打磨一次旋转60°，共抛光6次；（2）采用所提出的TSP 路径：同样进行6次抛光加工，每次生成随机点7200个，如图13所示。试验后，参数及结果统计如表5所示。

采用TSP 方法，当预设随机点数量与谢尔宾斯基方法获得的点数量接近时，每次生成路径的时间以及路径总长度均是每组试验中最小的。试验最后，本文所提出方法的抛光表面粗糙度数值略好于采用谢尔宾斯基路径。

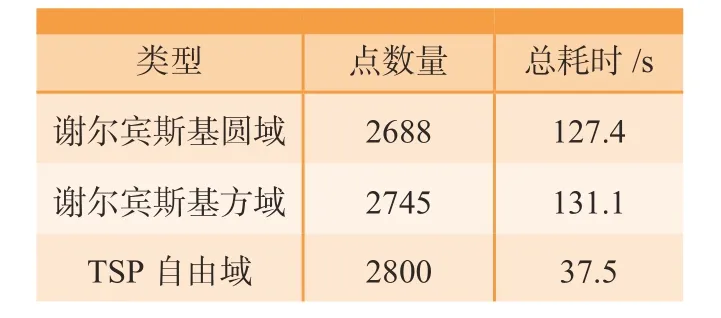
表4 计算数据统计Table4 Statistics of calculation results

图12 抛光试验Fig.12 Polishing experiment

图13 TSP 抛光路径Fig.13 TSP polishing path

表5 参数及结果统计Table5 Statistics of TSP parameter and calculation

结论

本文提出了一种基于TSP 方法的柔性抛光轨迹规划方案。它以自适应选择的边界参数化获得平面形状，将点位换算到重心坐标系并具有TSP 点的预设数量的功能。根据自适应选择标准，该映射域可以选择正方形、圆形或自由边界域。在已经满足预设的系统精度要求的前提下，确定抛光的初始TSP 点数。本文提出的方法主要可以解决以下问题：

（1）解决了TSP 轨迹规划问题，在保证加工精度的同时，可以有效控制预设的随机点数。

（2）根据不同的投影平面圆形度数值，调用自适应方法确定选择形状。

（3）通过比较链接路径长度和时间消耗的结果，如果抛光点的数量相对较大，我们建议使用蚁群算法求解TSP。

（4）自由边界域对边界的覆盖较好，但是需要增加判断随机点落在自由边界域的过程，路径计算耗时要大于圆域及方域。

（5）通过试验结果可知，本文所提出的方法在计算时间及路径长度上均优于谢尔宾斯基路径且精度较高。