小学数学高阶思维能力的培养策略

农梅英

【摘要】本文以“植树问题”的教学为例，论述小学数学高阶思维能力的培养策略，建议教师寻找知识点的内在联系，让学生的思维由“单点结构”衍生为“多点结构”;让学生动手画图，培养学生的数形结合思想;将问题化繁为简，让学生感悟化归思想;深入拓展，强化学生的应用能力;总结提升，建立数学模型思想。

【关键词】小学数学 高阶思维能力 植树问题

【中图分类号】G 【文献标识码】A

【文章编号】0450-9889（2021）05-0102-02

高阶思维是指发生在较高认知水平层次上的心智活动或认知能力。高阶思维能力是人类适应时代高速发展的必备素养和关键能力，它包括了问题解决、决策制定、批判性思维和创造性思维能力等多方面。[1]可见，培养学生的高阶思维能力对学生的人生发展是何等重要。在小学数学教学过程中，教师可以根据学科的特点，通过探索知识的内在联系、渗透数形结合思想、感悟化归思想、强化知识应用、由拓展到建模等多层次教学，发展学生的高阶思维能力，从而实现培养学生数学核心素养的目的。本文以人教版小学数学教材五年级上册“植树问题”的教学为例，探寻小学数学高阶思维能力的培养策略。

一、联系内在，思维由“单点结构”衍生为“多点结构”

数学知识不是孤立存在的，而是彼此存在联系。因此，教师在教学数学知识时，要善于找到知识点的内在联系，让知识点之间形成有机的整体，使学生的数学思维由“单点结构”衍生为“多点结构”，从而提高学生分析问题和解决问题的能力。

“植树问题”从教材的编排体系上属于“数学广角”，它要求学生结合情境发现问题、提出问题、分析问题和解决问题，培养的是学生的综合实践能力。在教学过程中，教师应引导学生发现问题，发现知识点的内在联系。

【教学片段1】

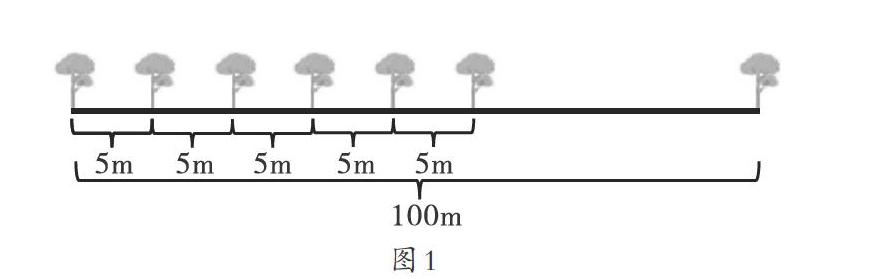
出示例题：在全长100m的小路一边植树，每隔5m栽1棵树（两端要栽），一共要栽多少棵树？

师：同学们，看到这个问题，首先会让我们想到什么呢？

生1：如果把100m的小路看成一条线段，每隔5m栽1棵树，让我想到了平均分的问题。

生2：这个问题就是把100m的线段平均每5米分一小段，看看能分成多少段。要用除法。

在教师的引导下，学生把“植树问题”和除法问题（平均分问题）联系起来，在脑海中出现以下图画（如图1）。

通過观察和分析，学生发现了“植树问题”和除法问题（平均分问题）的内在联系，发现了先求出“段数”是解决“植树问题”的关键所在。这样教学，不仅帮助学生把数学思维由“单点结构”衍生为“多点结构”，还促使学生把数学知识内化为自己的认知结构，有利于学生高阶思维的形成。

二、动手画图，培养学生的数形结合思想

我国著名数学家华罗庚先生说：“数缺形时少直观，形少数时难入微。”[2]五年级的学生大多数还处于形象思维阶段，通过数形结合将抽象数字与直观图形进行转换，可以有效提高学生分析问题的能力，有利于培养学生的高阶思维。

【教学片段2】

师：就像×同学所说，“如果把100m的小路看成一条线段，每隔5m栽1棵树”，我们怎样才能简明、形象地找出100m与5m之间的数量关系？

生1：可以画出图形试试。

师：是的。我们可以动手画出线段图，分析100m与5m之间的数量关系。

学生通过动手画线段图，很快发现了100m与5m之间的数量关系，并列出式子“100÷5=20（段）”，计算出段数。数形结合是让学生在解决数学问题时，用感性的方式表达出理性思维，这样不仅可以把抽象的数学概念、解题思路和直观形象的图像结合起来，还可以让学生的思维轨迹可视化，促进学生高阶思维的发展。

三、化繁为简，让学生感悟化归思想

化归思想是归结、转化思想的简称，就是将一个问题化难为易、化繁为简。在解决繁复的数学问题时，教师要善于引导学生感悟化归思想，让问题化繁为简，探索数学知识的本质规律，培养学生的逻辑思维能力。

【教学片段3】

师：同学们已经列出了式子“100÷5=20（段）”，计算出段数，但是段数就等于要栽种的棵数吗？

（有的学生认为是，有的学生认为不是）

师：我们可以画出线段图来验证一下。看看段数是不是等于要栽种的棵数。

生1：100m这么长，怎么画线段图呢？

师：我们可以先把问题化归为简单问题。假设要在全长20m的小路一边植树，每隔5m栽1棵树（两端要栽），一共要栽多少棵树？同学们可以试画出线段图。（如图3）

（学生画出线段图并计算树的棵数）

师：那么，如果要在全长25m的小路一边植树，每隔5m栽1棵树（两端要栽），一共要栽多少棵树？（如图4）

（学生继续画出线段图并计算树的棵数）

师：从这些线段图和计算结果中，我们能发现什么规律吗？同学们可以运用合理推理思想，列表进行归纳。

（学生通过自主探索、合理推理，完成表1）

学生通过自主探索、合理推理发现：“在全长20m的小路一边植树，每隔5m栽1棵树（两端要栽），一共要栽多少棵树”与例题“在全长100m的小路一边植树，每隔5m栽1棵树（两端要栽），一共要栽多少棵树”的实质是一样的，只是前者比后者更简单。教师通过引导学生运用归化思想，把复杂问题变得相对简单，让学生可以从简单的问题入手进行研究，便于学生发现数学问题的本质规律，得出了“总长÷间隔=段数，段数+1=棵数”的结论。这一规律不仅可以应用于解决“总长是500米、5000米、50000米……间隔是4米、8米、10米……”的植树问题中，还可以应用到解决与植树问题类似的“路灯问题”“敲钟问题”“桥墩问题”等问题中，提高了学生的知识应用能力和高阶思维能力。

四、深入拓展，强化学生的应用能力

拓展就是在原有的基础上增加新的东西，让学习的效果产生质量的变化。通过拓展学习，不仅可以让学生加深对知识点的理解，还可以让数学知识得到内化，提高学生的应用能力，为数学建模奠定基础。

【教学片段4】

师：刚才我们分析两端要栽的“植树问题”，将问题变化为——在全长100m的小路一边植树，每隔5m栽1棵树，①只栽一端，一共要栽多少棵树？②如果两端都不栽，一共要栽多少棵树？

学生运用前面的分析方法，画出线段图，列出表格进行合理的推理，进而得出结果。

生1：如果只栽一端，栽种的棵数=段数=100÷5=20（棵）。

生2：如果两端都不栽树，栽种的棵数=段数-1=100÷5-1=19（棵）。

通过拓展学习，学生可以将已学习的数学方法进行多次练习，将这些数学方法铭刻于头脑当中，逐步形成自己的高阶思维。

五、总结提升，建立数学模型思想

模型思想又称为数学建模，是学生从现实生活客观存在的事物（或具体生活情境）中经过观察、分析、思考、推理、验证，抽象出数学问题，并利用数学的方法表达出来。数学建模是学生高阶思维能力的体现，教师在教学过程中要逐步培养学生的建模素养，从而提高学生的高阶思维。

“植树问题”的研究过程就是一个数学模型的建模过程。（如图6）

总之，小学数学教师要把教学的着眼点放在对学生高阶思维能力的培养上，通过多层次的教学，培养学生的高阶思维能力，提高学生的数学核心素养。

【参考文献】

[1]（美）洛林.W.安德森.布鲁姆教育目标分类学（完整版）[M].北京：外语教学与研究出版社，2020

[2]赵红.图像表征：儿童理解数学的助推器[J].小学教学参考，2019（7）

[3]周彦.渗透数学思想 促进有效教学[J].新一代，2017（13）

（责编 雷 靖）