基于自适应引力算法的桥梁监测传感器优化布置

高 博，柏智会，宋宇博

(兰州交通大学 机电工程学院，兰州 730070)

桥梁的健康监测是测量桥梁在损伤条件下的动力特性和结构参数改变量，对比其在无损状态下的信息，并制定出最佳的维护方案[1]。传感器优化布置方案对桥梁健康监测的测试精度和参数分析有着直接影响。考虑到经济性和结构特征，要求桥梁上安装的传感器数量有限，因此，如何利用有限的传感器测点代表整体结构的运行状况和完整信息显得十分重要。传感器优化布置原理是从N个待测点中挑选出M个布设点，使目标函数达到最优的过程。其实质是组合优化问题，由于最终布置结果的复杂性和多样性，成为当今学者的热门研究课题。

目前已有许多成熟的传感器布置方法，其中传感器优化布置方案主要分为两类，一类是传统优化方法：Kammer等[2]提出的有效独立法是以模态矩阵为理论基础，将测点独立性的贡献值作为判定准则，依次删除贡献最小的测点，最终留下线性无关性最大的点作为传感器布置方案；Carne等[3]提出的模态置信准则(modal assurance criterion ，MAC)，将MAC矩阵的非对角元素最小化作为目标函数，发现MAC可以较好的反映梁模态向量的识别性；Guyuan缩减法[4]是利用刚度质量比小的位置更能反映结构的模态特性，将传感器布置在缩减后的位置。上述方法得到的结果往往是局部次优点，存在优化效率较低，寻优性能差的缺点，并不能达到理论与实际值误差最小的要求。第二类群智能优化算法，凭借其优秀的搜索和开发能力，在传感器布置中取得了快速发展：Dinh-Cong等[5]将Jaya算法应用到传感器优化布置和复合结构的损伤识别，发现可以成功找到损伤部位；Bruggi等[6]在传感器布置时采用拓扑方法进行优化，并在板结构的损失识别验证了算法的可行性；Wang等[7]提出了基于频率和空间域分解的方法，对四跨桥结构进行模态分析和损伤识别；Jin[8]提出了使用模态置信准则结合改进的和声搜索算法，应用在起重机传感器布置并验证了其优越性；Yi等[9]将自适应猴群算法采用双重编码的方式应用在高层建筑，发现更稳定的最优解；杨振伟等[10]引入等级划分和免疫机制，将改进的萤火虫算法应用在桥梁传感器布置，寻优效率取得显著提高。黄民水等[11]提出了基于二重编码的遗传算法应用于桥梁结构的健康监测；赵建华等[12]把惯性权重递减的粒子群算法结合模态置信准则，发现在二维桁架结构中能找出传感器的优化位置。以上基于群智能算法的传感器布置方法依然存在一定的局限性，如对于同一研究对象，不同的研究方法得到的传感器布置方案往往不同，因此算法的可靠性验证仍需进一步改善。

引力搜索算法(gravity search algorithm,GSA)[13]凭借其容易实现，可操作性好，优化效果明显的优点，在生产实践中得到广泛应用[14-17]。GSA算法也存在搜索能力较弱的缺点，本文对GSA算法进行改进，通过对引力常量G中衰减因子α的自适应调整，以改变粒子不同时期的步长，来改善算法性能，提高算法搜索能力。将改进后的自适应引力算法(adaptive gravity search algorithm,AGSA)通过双重编码的方式，结合MAC准则，提出了基于AGSA算法的传感器优化布置方案。以马水河大桥为实例，验证AGSA算法的有效性，发现改进后的AGSA算法在传感器优化布置优于遗传算法(genetic algorithm,GA)得到的结果。

1 传感器优化准则

现有的传感器优化准则如模态动能法由于高度依赖有限元网格的划分精度，会影响数据的可靠性；模态缩减准则存在容易丢失待测模态的缺点，增加识别难度。在实际生产中，由于受到外在因素：测量仪器的精度误差、测试场所的噪声干扰等，会导致得到的模态向量夹角过小，甚至为0的情况，而导致模态信息丢失的情况。故传感器优化布置的测点应选取空间中模态夹角较大，易识别的点。MAC可以选择较大的空间交角,尽可能保留原模型的特性。保证了模态的正交性和模态信息的完整性。故可以将MAC作为传感器优化布置的适应度函数，用来评价各阶测试振型的独立性。MAC的表达式为

(1)

式中，φi和φj分别为第i阶和第j阶模态向量。

研究表明，MACij(i≠j)的值介于0～1，反映对应模态向量的空间夹角。其中MACij(i≠j)的值越接近于0，说明对应的空间夹角越大，i阶和j阶模态向量越接近正交；MACij(i≠j)的值越接近于1，说明对应的空间夹角越小，i阶和j阶模态向量越接近平行。一般地，当MACij(i≠j)值小于0.25，即可认为两模态向量容易识别。MAC矩阵的非对角元素值越小，表明计算的模态向量独立性越好，其模态振型越容易识别。因此可以将MAC矩阵的最大非对角元素最小化作为桥梁传感器布置的适应度函数，表达式为

fitness=minf(x)

(2)

2 基于自适应的引力搜索算法

引力搜索算法是利用粒子之间受到万有引力的吸引作用，种群中质量最大的粒子占据最优位置，其他粒子在万有引力的作用下向质量最大的粒子移动，得到所求问题全局最优解的过程[19]。假设算法中有M个粒子，以其中某一粒子i为例，粒子i受到其他粒子的万有引力，在合力作用下产生加速度a和速度v，使粒子i下一时刻向全局最优解靠近的过程。引力常量G自始至终贯穿于算法的整个搜索过程，其取值的变化过程会直接影响算法的搜索效率和寻优精度，GSA算法中的衰减因子α的取值时一个常数，这会导致粒子在搜索过程以固定的步长移动。为了增强算法的优化能力，本文提出的AGSA算法对α进行自适应调整，搜索初期粒子距离最优解较远，粒子以较大步长进行全局搜索；搜索后期粒子靠近最优解的邻域，粒子采取小步长搜索，有利于算法局部搜索，有效找到全局最优解。

2.1 引力搜索算法

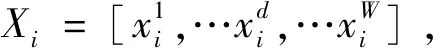
(3)

式中：Mi(t)和Mj(t)分别为粒子i，j的惯性质量；G(t)为t时刻的万有引力系数；R为粒子i与粒子j之间的距离；ε是为了保证分母不为0的非常小的数。

G(t)的计算公式为

(4)

式中，α为常数;Imax为最大迭代次数。

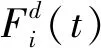
(5)

式中，best为对粒子i有引力作用的粒子的集合。

(6)

式中，Mass(i)为粒子i的惯性质量，其计算公式为

(7)

(8)

式中，fitnessb(t)和fitnessw(t)分别为最好的适应度值和最差的适应度值。

下一时刻粒子i的速度和位置公式为

(9)

式中，rand1，rand2为[0，1]的随机数。

2.2 改进的自适应引力搜索算法

引力常量G(t)对算法的收敛速度和寻优精度具有重要影响。式(4)中的α具有调节算法收敛速度的作用[20]。针对GSA算法的寻优效率和搜索精度问题，本文对GSA算法进行了改进，提出了AGSA算法。考虑到GSA算法中α的取值是一个常数，这就会导致粒子距离最优解较远时，步长太小，移动过慢，花费时间太长；粒子距离最优解较近时，步长太大，可能出现偏离最优解，陷入局部最优解的情况。因此，改进后的AGSA算法在搜索前期选取较小的衰减因子α，粒子以较大的步长进行全局搜索，有利于减少算法的搜索时间，提高整体寻优效率；算法的后期选取较大的衰减因子α，粒子对应较小的步长完成局部搜索，避免算法落入局部极值点。自衰减因子α的自适应原理是迭代初期对应的衰减因子α取较小值，对应的G取值较大，有利于粒子进行全局搜索；迭代后期衰减因子α不断增加接近β，对应的G取值较小，有利于粒子进行局部搜索。自适应衰减因子α表达式为

(10)

式中：t为当前迭代次数；β为初始参数，根据经验，当β=40时，算法的寻优效果最佳，β的取值具有通用性，不受桥梁规模和所选桥型的影响。

AGSA算法的原理图如图1所示

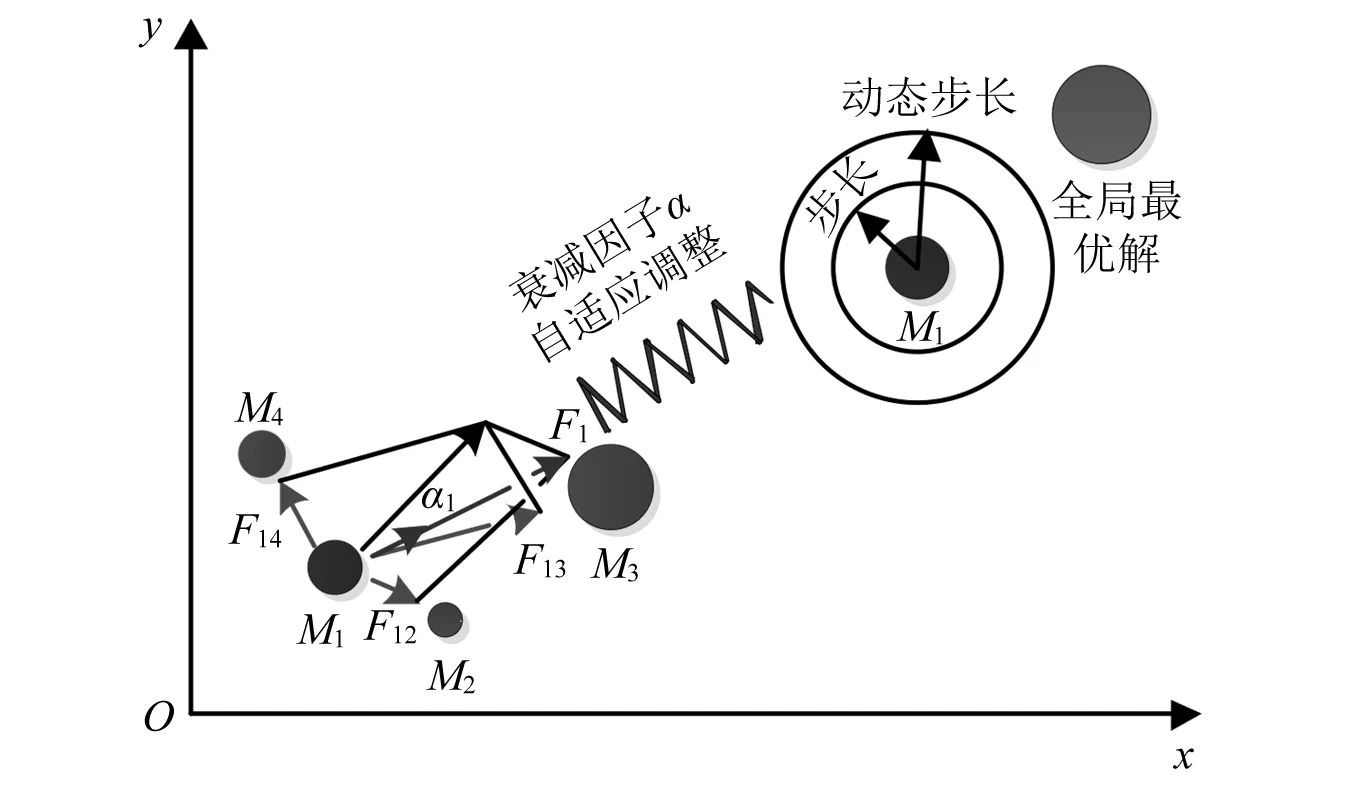
图1 AGSA算法原理图Fig.1 Schematic diagram of AGSA

图1中，粒子M1在M2，M3，M4的万有引力作用下产生了合力F1和加速度a1，通过衰减因子α的自适应机制，粒子M1以不同的步长向全局最优解靠近。

3 基于自适应引力的传感器优化布置

3.1 种群初始化及编码

GSA算法当前主要应用在连续优化问题的求解，传感器优化布置是类似于0-1规划的离散型问题，因此需要将引力搜索算法改进为适合整数规划的优化算法。本文采用一种双重编码的方式,双重编码的方法如表1所示。

表1 双重编码方式Tab.1 Dual-structure coding method

利用附加码xi和变量码si组成的有序对(xi,si)表示种群中个体i对应的传感器布置结果[21],(xi为i的位置向量;si为二进制向量0或1，其中，0为不布置传感器，1为布置传感器)，这种双重编码的方式使得AGSA算法可以解决传感器优化布置问题。例如，已知有8个待选点，它们的附加码为x=(5,3,6,1,4,7,2,8),其双重结构编码结果如表2所示，由表2可以知道变量码对应的布置方案为s=(3,4,5,8)。

表2 双重编码结果Tab.2 The result of dual-structure coding method

3.2 基于AGSA算法的传感器优化布置过程

步骤1选择和导入模态矩阵。模态矩阵阶数的选择对传感器布置结果有重要影响，一方面，适合的模态矩阵可以代表结构的整体性能，保证布置方案的准确性；另一方面，不同的模态阶数，得到的布置方案有差异性。首先，建立马水河特大桥的有限元模型，利用模态分析的方法得到模型所有节点的模态振型矩阵，将得到的模态振型矩阵作为输入值，所有节点对应的自由度作为传感器布置的待选点，其次，假设待选点的数量为n，传感器布设点数量设置为m，对这n个候选位置依次从1-n进行整数编号。

步骤2设种群数量为N，粒子i对应的解可以表示为xs(i)=(xi,si)={(xi1,si1),(xi2,si2),…,(xin,sin)},xi的各个分量是区间[down,up]产生的随机整数，si的分量是由转换函数得到的二进制向量。

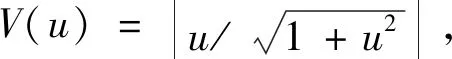
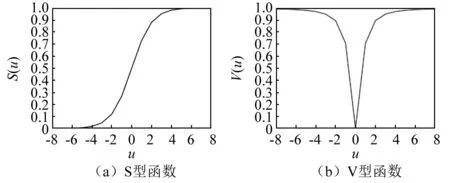
图2 转换函数Fig.2 Conversion function

刘勇等[22]发现并验证了V型转换函数的优化效果更好，故本文选取V型函数作为转换函数。si的分量按照下式转化为二进制向量

(11)

式(11)中，不同的位置分量xij计算得到的二进制值不同，因此需要设置一个阀值δ来满足

(12)

式中，j∈{1,2,…,f}，本文中δ=0.5，将xi的各位置分量代入式(11)中，若函数值大于0.5，附加码值为1，表示在该候选点布置传感器；若函数值小于0.5，附加码值为0，表示在该候选点不布置传感器。通过计算可以得到xij的取值在[-8,8]时取值时，si的分量取值0≤V(xij)≤0.992 3，可以近似代替[0,1]。故down=-8，up=8。

步骤3按照步骤1和步骤2，随机产生种群数量为N的粒子位置，其中，每个粒子的位置都表示一种传感器布置方案。

步骤4把种群中的N个粒子依次代入适应度函数fitness(xsi)。在计算过程中，位置向量通过转化函数V(xij)转化为二进制向量sij，将sij代表的传感器位置对应的模态矩阵计算适应度函数，最好的适应度值标记为fitnessb(xsi)，最差的适应度值标记为fitnessw(xsi)。最好适应度值对应的布置方案记为pi(xsi)，pi(xsi)代表种群中粒子的个体最优解，是每个粒子迭代中的最优解。pg(xsi)表示全局最优解，是种群中所有粒子中的最优解。

步骤5利用式(7)和式(8)，计算每个粒子的惯性质量；按照式(9)对衰减因子α进行自适应改变，更新引力常量G(t)。

步骤6以粒子i为例，其对应的位置分量xi={xi1,xi2,…,xim}，其中m为需要布设的传感器数目，计算粒子i与其他粒子的欧式距离，利用式(3)和式(5)，得到粒子i在其他粒子作用下的合力，利用式(6)计算粒子i受到的加速度。同理计算出种群中其他粒子受到的万有引力和加速度。

步骤7为加快粒子收敛速度，在粒子速度公式中引入变异算子η，增加全局最优解对粒子的引导作用，变异算子的表达式如式(13)所示，在更新位置的过程中，计算得到的加速度和速度分量会出现非整数的情况。因此，本文中位置更新如式(14)所示。

(13)

(14)

式中，round为取整函数，保证更新后的粒子位置分量是整数形式。

步骤8将更新后的粒子对应的模态位移代入式(2)，若更新后的fitness(xsi)值小于更新前的，则粒子位置发生改变，否则，粒子位置保持不变。更新后的最优适应度值对应的布置方案记为pb(xsi)，若更新后的最优适应度值fitness(pb)小于更新前的全局最优值pg(xsi)对应的适应度值fitness(pg(xsi)),则用当前粒子代替全局最优解，反之，全局最优解保持不变。

步骤9判断算法是否达到预设的精度要求或最大迭代次数，若满足，停止迭代，输出全局最优解，即为需要的传感器布置方案；若不满足，返回到步骤5。

注1粒子的位置分量是从[-8,8]中随机产生的整数，在步骤7中，粒子在位置更新中，可能会出现超出取值范围的情况。因此，本文规定，当位置分量大于8时，取8；当位置分量小于-8时，取-8。

基于AGSA的流程图如图3所示。

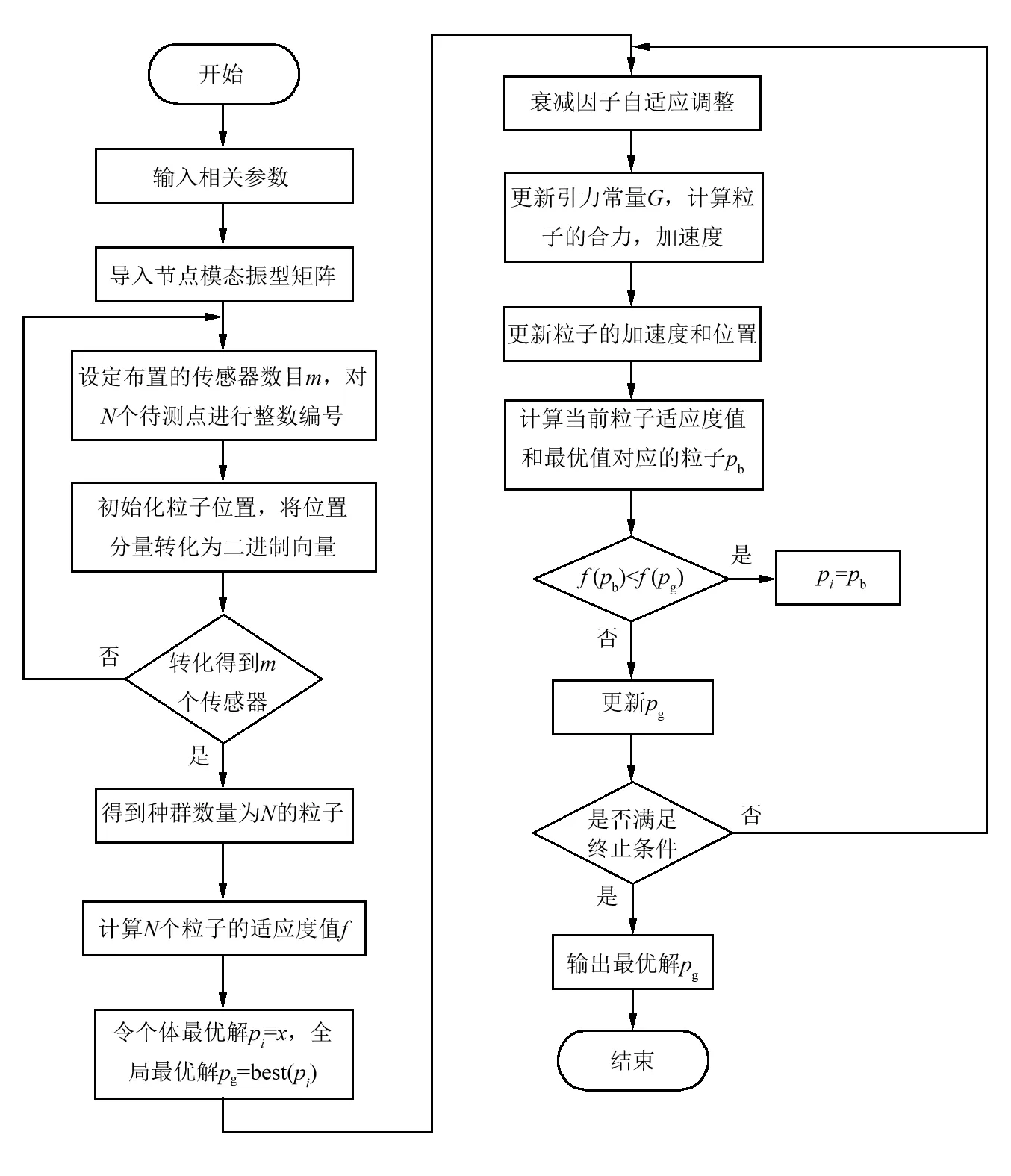
图3 基于AGSA的流程图Fig.3 Flow chart based on AGSA

4 模型验证

4.1 计算模型

为了验证本文提出的算法在传感器优化布置的有效性，本文以马水河大桥为例，如图4所示，桥梁全长955.80 m，桥面中心设计标高654.355 m，主桥上部采用110 m+3 m×200 m+110 m，全桥为单箱单室，桥面宽12.5 m，梁底宽6.5 m，梁高3.50～12.00 m；主桥下部共有4座桥墩，承台厚度为4.0 m。考虑到马水河特大桥在施工时会受到温度，预应力拉伸等因素的影响，将桥梁模型简化为平面刚架，各施工段按照梁单元计算，导入到ANSYS进行模态分析。模型共有442个节点，436个单元，每个节点包含3个自由度，分别对应x，y，z方向的模态信息。并导出结构的前10阶模态振型。由于x和z方向模态位移均接近于0，因此本文只考虑y方向的模态位移。桥梁结构的前10阶固有频率及振型描述如表3所示。

图4 桥梁计算模型Fig.4 Bridge calculation model

表3 桥梁固有频率及振型描述Tab.3 Description of natural frequency and vibration mode of bridge

4.2 自适应引力算法布置方案

根据本文提出的自适应引力搜索算法进行传感器布置。设定种群数量为N=100，迭代次数为Imax=20，β=40,G0=100,算法重复运行10次，分别计算布设点m为8,12,16时，目标函数的最优值，最差值，以及平均值。其最优布置方案和迭代曲线分别如表4和图5所示。

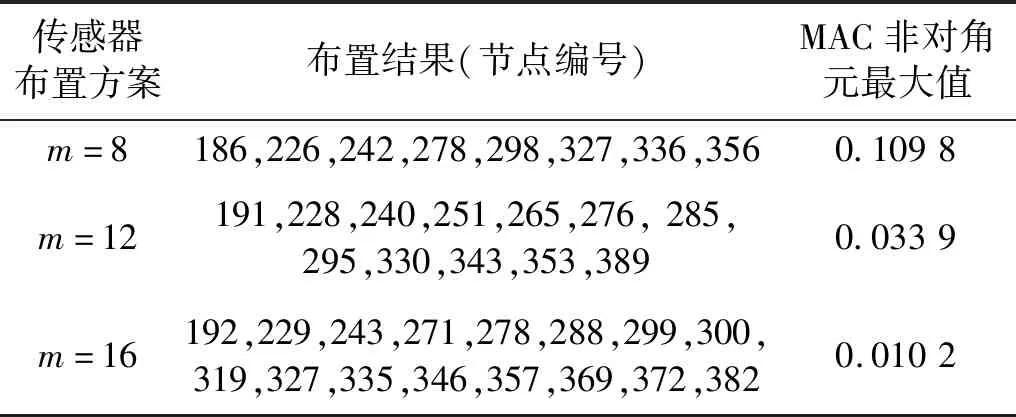
表4 传感器布置方案Tab.4 Sensor placement

由图5可知，不同的传感器数量对应的适应度函数值不同，当布置的传感器数量m分别为8，12，16时，目标函数的平均值分别为0.132 4，0.046 6，0.018 8。结果表明随着m的增加，目标函数的平均值越小，搜索得到的模态向量更容易识别；目标函数的最优值依次可以达到0.109 8，0.033 9，0.010 2。说明在一定的取值范围内，随着传感器数量的增加可以得到的布置方案更优。

图5 自适应引力算法迭代曲线Fig.5 Iterative curves of adaptive gravitation algorithms

一般来说，传感器布置的数量越多，可以得到结构的布置信息越多，越能反映结构的健康状况。但在实际应用中，由于传感器成本较高，不可能布置太多的传感器，传感器数量的选择显得至关重要。故本文以传感器数量为自变量，以式(2)为目标函数，每组变量计算10次，10次运行结果的平均值为应变量，变化曲线如图6所示。可以看出传感器数量在0～8时，目标函数的下降曲线较快，当传感器数量在15～20时，目标函数值趋于稳定。因此，本文选取m=16作为最终布置的传感器数量。

图6 传感器数量与目标函数曲线Fig.6 The curve of sensors number and objective function curve

同时，为了验证所选模态阶数对传感器优化结果的影响，本文探讨了传感器数量设定m=16，模态阶数分别为6,7,8,9,10时，通过AGSA算法最终得到的传感器优化布置结果和对应精度如表5所示。

由表5可以看出，随着模态阶数的增加，MAC矩阵非对角最大值出现增大的趋势。但从表中可以看出不论模态阶数选取6阶还是10阶，最终得到的目标函数值远小于0.25，也证明了AGSA算法的有效性。

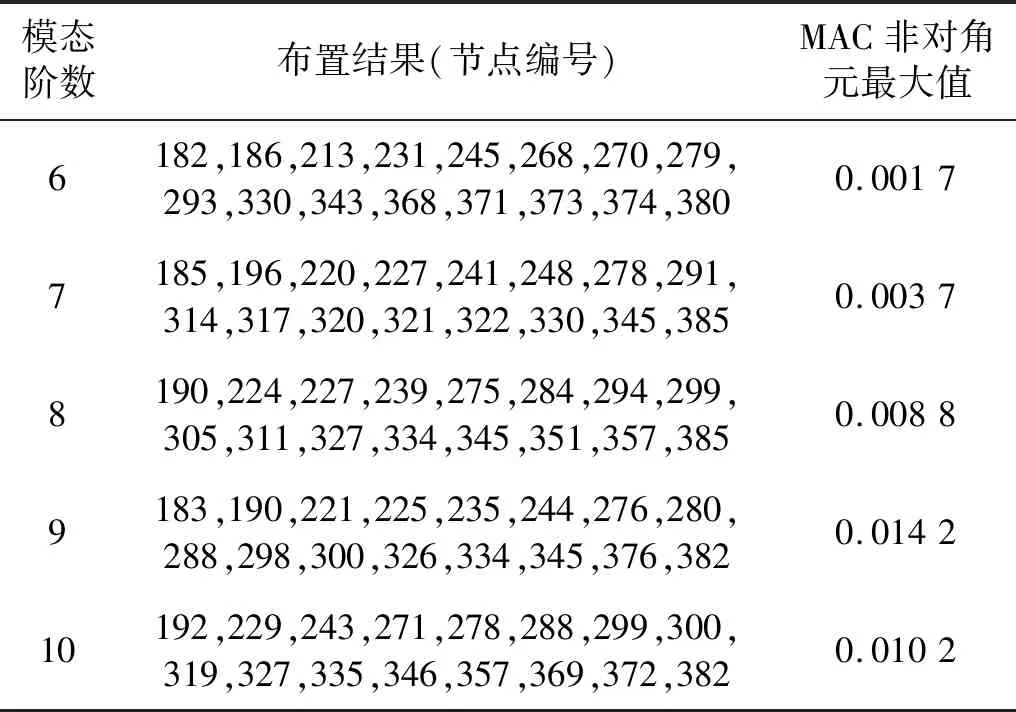
表5 模态阶数对优化结果的影响Tab.5 Effect of modal order on optimization results

4.3 优化布置结果分析

为了进一步突出AGSA算法的优越性，比较AGSA算法和GA算法在布置16个传感器时的结果。图7给出了两种算法的MAC矩阵柱形图。一种是GA算法[23]得到的传感器布置方案;另一种是AGSA算法得到的传感器布置方案。GA算法得到的MAC矩阵非对角元最大值为0.169 0，虽然小于0.25，但是个别位置还存在不宜分辨的情况；相比GA算法，AGSA算法的非对角元最大值为0.010 2，效率提升93.96%，也说明本文提出的基于AGSA算法是有效性和可行性。考虑到图7中MAC矩阵的非对角元素值太小，图8给出了两种算法布置方案对应的MAC矩阵每个模态列向量非对角元最大值。由图8可以清楚的看出AGSA算法的MAC矩阵的最大非对角元明显小于GA算法得到的结果。这也验证了AGSA算法对应的模态向量区分度更高，布置方案更优。表6给出了两种算法的传感器布置方案。

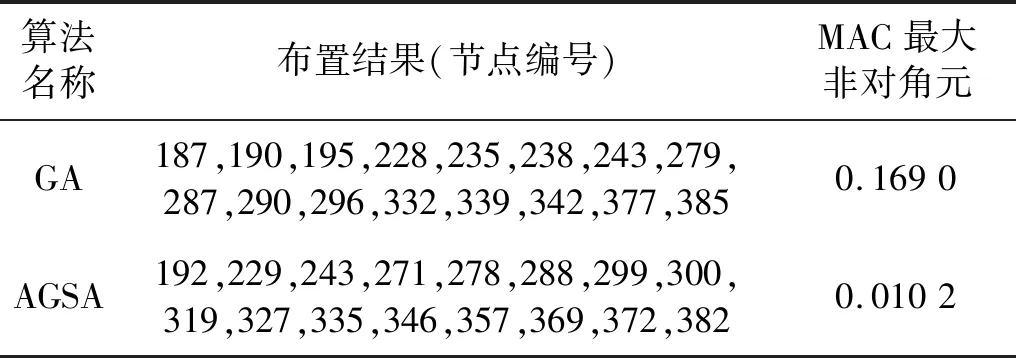
表6 两种算法的布置方案Tab.6 Sensor placement of two algorithms

图7 两种算法的MAC矩阵Fig.7 MAC matrix under two algorithms

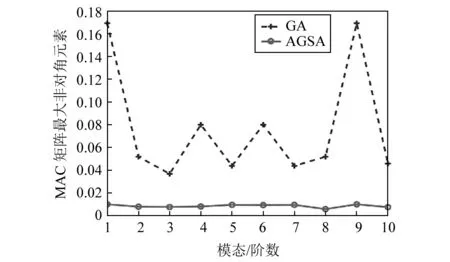
图8 MAC矩阵每个列向量最大非对角元Fig.8 Maximum MAC off-diagonal value in each of the modes

5 结 论

本文针对GSA算法只能解决连续性函数的优化问题，提出了可以解决离散型问题的AGSA算法，并将其应用到马水河大桥的传感器优化布置中，将其布置结果与遗传算法得到的结果比较，得到以下结论：

(1)针对GSA算法搜索效率和寻优精度不高，本文提出的AGSA算法对引力常量G中的α进行了改进，确保粒子在不同的搜索时期，进行全局搜索和局部精细搜索，提高了算法的全局搜索能力。

(2)为了AGSA算法可以解决离散型的传感器优化布置问题，本文采用双重编码的方式，将AGSA算法应用到传感器布置中，克服了二进制编码导致的迭代过程中，传感器数量发生改变的缺点。试验结果表明，该方法可以有效解决传感器优化布置问题。

(3)AGSA算法通过多次试验，发现传感器数量选择对目标函数的精度影响较大,在初始阶段，目标函数值随传感器数量的增加而不断减小；当数量增加到一定范围，目标函数值趋于稳定。

(4)以马水河大桥为例，将AGSA算法和遗传算法得到的布置方案相比较，结果表明，AGSA算法的可靠性，寻优效率都优于遗传算法，证实了本文提出的AGSA算法适用于传感器优化布置，也表明该算法可以满足大型桥梁健康监测的需求。