压电集成碳纳米管CNT增强功能梯度结构非线性建模与仿真

王 雄，高英山，张顺琦，薛 婷，陈 敏

(1.榆林学院 能源工程学院，陕西 榆林 719000；2.上海大学 机电工程与自动化学院，上海 200444；3.西北工业大学 机电学院，西安 720071;4.西交利物浦大学 电子系，江苏 苏州 215123)

功能梯度材料(functionally graded materials,FGM)是一种多相材料，由基体和增强体构成，且各个组成成分可以沿某一方向连续变化，各组成成分的含量变化具有一定的可设计性，易获得质量轻、强度高、隔热性能好的结构形式[1]，其内部没有明显的界面分层问题，还具有良好的机械和热力学性能[2]，因此广泛应用于航空航天、电子工程[3]以及生物医学等领域。在1991年碳纳米管(carbon nanotube,CNT)被发现[4]。Shen[5]首次提出将梯度形式分布的CNT与基体材料结合，形成刚度高、重量轻、热机性能好的功能梯度材料，具有巨大的应用前景[6]。

Yas等[7]使用Timoshenko梁理论分析了在移动荷载作用下的线性连续均匀CNT复合材料梁的振动特性。Lei等[8]研究了CNTs/FG 板的屈曲行为，研究表明临界屈曲载荷随CNTs 体积分数的增加迅速提升。贺丹等[9]采用一阶剪切变形(first-order shear deformation,FOSD)理论和哈密顿原理研究了适用于CNT功能梯度板的自振模型。姚小虎等[10]采用有限元法分别对单壁碳纳米管的轴压屈曲行为，后屈曲行为进行模拟实验。在非线性建模方面，Shen[11]提出了一种二阶摄动方法，研究了在热环境下受横向均匀或正弦载荷作用的简支功能梯度CNT增强复合材料板的非线性弯曲问题；Ke等[12]分析了CNTs/FG板的非线性自由振动问题，发现CNTs 能够有效的增加结构刚度。Zhang等[13]采用弧长迭代法和修正Newton-Raphson法得到了FG-CNT增强复合板的非线性响应。既有基于FOSD变形理论[14-15]也有基于高阶剪切变形(high-order shear deformation,HOSD)理论[16]建立非线性模型，对带有压电片的FG-CNT增强复合板进行了分析。以上模型都是基于冯卡门非线性，只能用于小转角的薄壁结构非线性分析。在Kreja等给出薄壁复合结构大转角几何全非线性分析方法后，Zhang等[17-18]采用大转角板壳理论对复合薄壁结构进行了建模和分析。此外有很多综述方面的文章对CNT方面的研究方向和内容进行了综述[19-20]。

通过文献调研可知，对CNT梯度增强薄壁结构发生大转角大变形的研究几乎没有。为此，本文基于Reissner-Mindlin板壳假设，建立FG-CNT增强复合板的大变形几何非线性有限元模型。首先将计算结果与文献中的数据进行对比，验证模型的正确性；然后对FG-CNT增强复合板进行非线性分析；最后，研究CNT不同的分布形式及CNT增强角度对FG-CNT和带有压电片的FG-CNT增强复合板刚度的影响。

1 FG-CNT增强复合板非线性有限元模型

FG-CNT增强复合板由CNT与各向同性的聚合物基体组成。根据广义混合分布模型，FG-CNT增强复合板的等效材料参数可以表示为

(1)

(2)

(3)

本文主要考虑四种不同的CNT分布类型，即均匀分布、V型分布、O型分布和X型分布，分别用FG-U，FG-V，FG-O，FG-X表示，如图1所示。

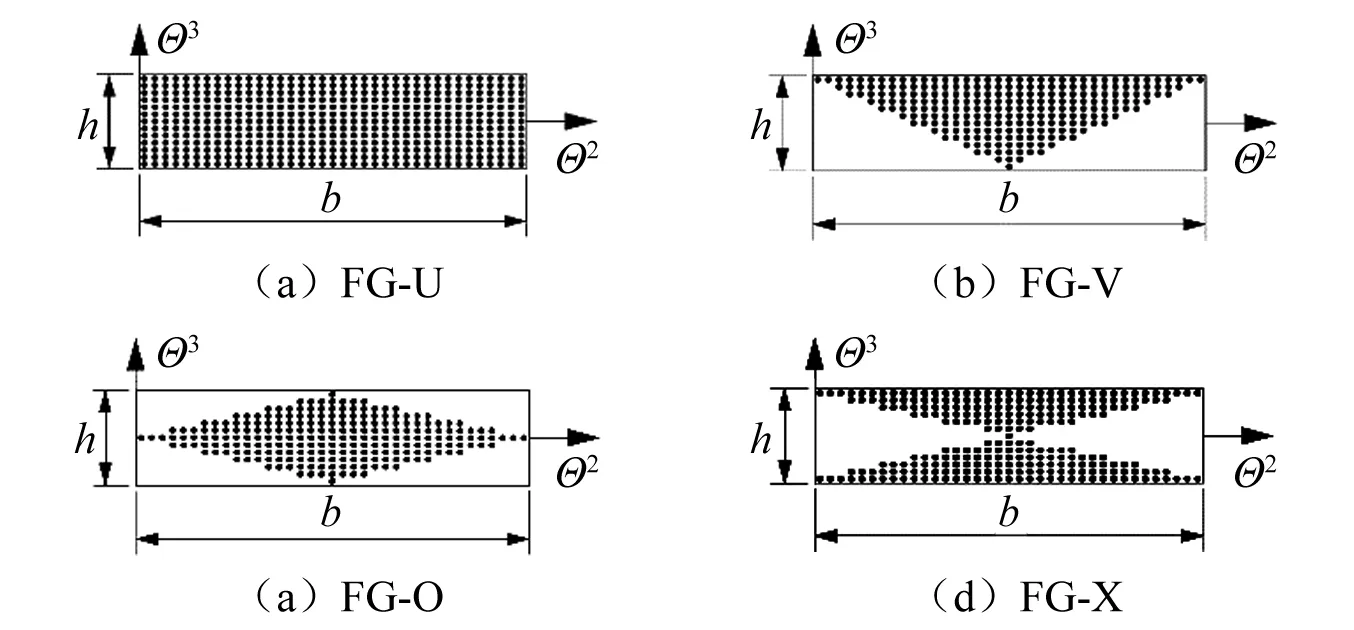
图1 不同分布类型下CNT增强复合板横截面图Fig.1 Cross section of CNT-FG structures of four typical distributions

FG-CNT增强复合板中的CNT体积分数与分布形式有关

(4)

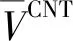
(5)

ρ=VCNTρCNT+Vmρm

(6)

基于FOSD变形假设，FG-CNT增强梯度板拉格朗日几何全非线性应变表达式为

(7)

(8)

式(5)和式(6)中各应变分量为

(9)

(10)

(11)

(12)

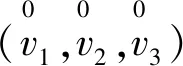
(13)

其中，

C66=G12,C44=κG23,C55=κG13

(14)

t+Δt时刻的应变由t时刻应变和无穷小时间步增量应变的总和

t+Δtε=tε+Δε,

(15)

同样的t+Δt时刻的位移可以表示为

t+Δtu=tu+Δu。

(16)

在t+Δt时刻结构动能、结构内功和外功虚功可以表示为

(17)

(19)

t+ΔtδT-t+ΔtδWint+t+ΔtδWext=0

(20)

可获得非线性的有限元方程

(21)

式中：tMuu，tKuu分别为质量矩阵、刚度矩阵；Fue,tFuu分别为外力向量和平衡力向量；q为节点位移向量；左上标t为变量处于当前时刻。求解过程可以参考Zhang等的研究。

2 非线性仿真分析

2.1 FG-CNT增强复合板结构及参数

本文中的FG-CNT增强复合板有聚合物基体和CNT增强体构成，这两种材料在室温下的参数如表1所示，认为G12=G23=G13。本文中CNT体积分数以及与之对应的效能参数ηi(i=1,2,3)如表2所示。

表1 材料参数Tab.1 Elastic properties of CNT and matrix

表2 不同的CNT体积分数对应的效能参数Tab.2 Efficiency parameters of different CNT volume fraction

2.2 模型验证

通过与文献[21]中四边简支(SSSS)的FG-CNT增强复合板前六阶无量纲化频率，ω*=ω(b2/h)(ρm/Em)1/2，比较来验证本文模型；板的长、宽、高分别用a,b,h表示，这里a=b=40 mm，h=2 mm，采用10×10的网格划分，8节点2次矩形单元，数据比较结果如表3所示。通过表3我们可以看出仿真数据与参考数据的差别小于3.308%，由此可以看出本文中的模型可以正确计算板壳问题。

表3 FG-CNT板无量纲化频率数据对比(a/h=20)Tab.3 Comparison of non-dimensional frequency parameters of FG-CNT plate(a/h=20)

2.3 非线性仿真

当结构发生大变形时，线性仿真已不能准确反映其变形，因此需要用非线性理论来仿真，获取与实际变形较贴合的结果。为了能够很好的观察非线性，对a=b=40 mm，h=2 mm四种CNT分布的FG-CNT增强复合板施加5 MPa压力，网格划分和单元类型同上，利用本模型计算得到的非线性与线性结果对比如图2所示。

图2 中心线位移图Fig.2 Displacements of central line

从图2(a)中可以看出，对CNT体积分数相等的FG-CNT增强复合板施加相同的力，非线性位移较线性小，不同分布之间的位移大小关系为FG-O>FG-V>FG-U>FG-X，即相同的CNT体积分数，X型的FG-CNT增强复合板的刚度最大，O型的FG-CNT增强复合板的刚度最小，从另一个角度来说就是CNT的分布集中在板的两表面时比集中在中间时的刚度大。随着CNT体积分数的增加，同种分布的FG-CNT增强复合板的刚度逐渐增大，这个可以从图2(b)中看出。

图3 中心点位移Fig.3 Displacements of central point

2.4 带有压电片的FG-CNT复合板仿真

在一些情况下需要在FG-CNT增强复合板上下两侧贴上压电片(PZT)，这里采用的是杨氏模量Y为63 GPa，泊松比υm为0.28的G-1195压电片。这里压电FG-CNT板长宽为的a=b=40 mm，压电片的厚度为0.2 mm，CNT功能梯度增强层的厚度为2 mm。示意图如图4所示。

图4 简支压电板Fig.4 Simply supported piezoelectric plate

从图5中可以看出，随着角度逐渐增大，中心点位移先是逐渐减小，45°达到最小值，即此时板的刚度最大；随着CNT增强角度继续增大，位移逐渐增大，且其位移关于角度为45°时对称。

图5 CNT增强角度对板中心点位移的影响Fig.5 The effect of CNT reinforcement orientation on the displacements of plate central point

3 结 论

基于Reissner-Mindlin板壳假设建立了复合板的大转角大变形几何非线性有限元模型。通过计算和分析CNT不同的分布形式、体积率和结构尺寸，得到如下结论:

(1) 研究CNT体积率和四种不同CNT分布方式对FG-CNT增强复合板刚度的影响，表明结构刚度随着CNT体积率的增加而增大；CNT体积率相同时，四种CNT分布方式板的刚度关系为FG-X>FG-U>FG-V>FG-O。

(2) 对于相同的CNT体积率和分布方式，在相同的载荷条件下，非线性建模方法得出的结果总是小于线性结果，且大转角非线性结果比冯卡门非线性的小。

(3)以四边铰支的方形板为例，研究CNT增强角度对板的刚度的影响，CNT增强角度为45°时，板的刚度最强，在线性和非线性时都得到验证。