基于车-桥耦合振动的铁路钢管混凝土系杆拱桥冲击系数研究

蔺鹏臻，王亚朋

(1.兰州交通大学 甘肃省道路桥梁与地下工程重点实验室，兰州 730070;2.兰州交通大学 土木工程学院，兰州 730070)

钢管混凝土系杆拱桥充分发挥梁受弯和拱受压的组合优势，具有跨越能力大、承载力高和抗变形能力强的优点，从而受到高速铁路立交桥型选择的青睬[1]。作为由预应力混凝土系梁、钢管混凝土拱肋和吊杆组合而成的结构，在高速铁路动载作用下容易产生结构体系性振动，影响列车运行平稳性和舒适性。国内外桥梁规范中对列车运行冲击效应的影响通过动力系数反应，其值不小于1.0[2]。我国TBTB 1002—2017《铁路桥涵设计规范》[3]对高速铁路桥梁结的冲击系数规定是与桥梁加载跨度关联的函数，但该公式当桥梁加载长度大于67.24 m以后冲击系数将恒为1.0。而现有高速铁路桥梁工程中，超百米跨径的系杆拱桥占较大比例，对于超过67.24 m的大跨度系杆拱桥，桥梁冲击系数如何取值还需要在考虑多因素列车运行条件下进行综合分析。

桥梁冲击系数与通过车辆类型、车速、桥梁跨度、桥梁宽度、桥梁基频、桥梁阻尼、车辆质量等因素相关[4]。朱志辉等[5]通过车-线-桥耦合动力学和虚拟激励法的吊杆随机动应力分析法，研究了轨道不平顺等级及车速对重载铁路拱桥吊杆应力冲击系数的影响，以及不同位置吊杆应力冲击系数的不均匀性。吴定俊等[6]应用车桥耦合振动理论分析了京沪高速铁路112 m跨度尼尔森体系钢管拱桥的冲击特性，得到位移的最大冲击系数可达1.33。马继兵等[7]通过对我国第一座铁路尼尔森体系钢管混凝土提篮式系杆拱桥的冲击实测表明，拱肋与桥面系具有不同的冲击系数，拱肋最大冲击系数达到了1.865，超过了设计规范限制。

本文结合某客运专线跨度136 m的钢管混凝土系杆拱桥，建立了车辆-桥梁动力相互作用模型，研究了在空载、满员2种荷载、30条随机不平顺样本、126种速度等级组合的7 560种动力分析工况下，铁路大跨度钢管混凝土系杆拱桥系梁、拱肋和吊杆的冲击系数变化规律，并基于概率统计假设检验理论，在保证率95%提出该算例系梁、吊杆、拱肋冲击系数，并研究冲击系数随速度变化规律，以期对该类型桥梁的冲击系数取值提供理论依据。

1 基于车-桥动力相互作用的分析模型

1.1 车辆子系统模型

采用多刚体动力学理论[8]，建立车辆空间三维多体动力学模型。每节车由1个车体、2个转向架、4个轮对和8个轴箱组成，其中车体、转向架、轮对均考虑伸缩、横移、沉浮、侧滚、点头、摇头自由度，轴箱仅考虑点头自由度，每节车共计50个自由度，各刚体自由度如表1所示。每节车考虑一、二系悬挂刚度及非线性阻尼器特性，以及车体横向止挡、牵引拉杆、抗侧滚扭杆特性。

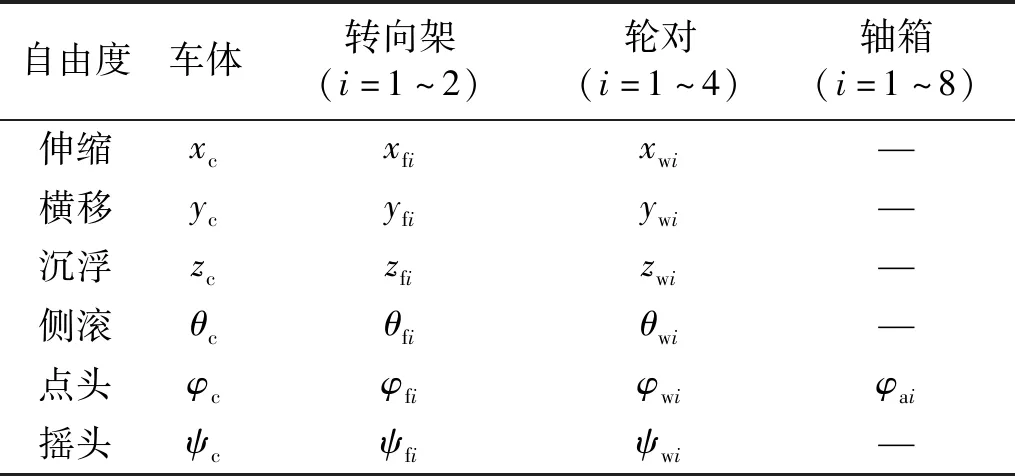
表1 车辆动力学模型自由度Tab.1 The degrees of freedoms of vehicle dynamic model

根据D′Alembert原理可建立车辆系统动力学方程

(1)

1.2 考虑桩-土效应的桥梁子系统模型

桥梁子系统的运动方程可表示为

(2)

上部结构梁体与桥墩之间采用支座连接。按支座设计类型，通过梁与桥墩结点的同位移实现墩、梁位移约束模拟。群桩桩基受桩周土体的约束采用基于“m法”的土弹簧模拟，在承台底部施加弹簧约束模拟群桩基础等效刚度[9]，实现对桩-土作用效应的考虑。

1.3 轮轨接触关系

车辆子系统与桥梁子系统之间的动力相互作用通过轮轨接触关系实现，轮轨间法向力由Hertz非线性弹性接触理论确定，接触斑上任意点法向力为[10]

(3)

式中:P为接触斑最大法向力；a,b分别为接触斑的短半轴和长半轴。

轮轨切向力根据Kalker非线性简化理论计算

(4)

式中：px,py分别为纵、横向蠕滑力；L为柔度系数；sx,sy分别为切向蠕滑速度；ξx,ξy,φ分别为纵、横向及自旋蠕滑率。

1.4 车-桥耦合系统模型建立及轮轨力求解

将车辆子系统和桥梁子系统通过轮轨接触关系组成整个耦合时变系统，建立车-桥耦合时变系统动力学方程。本文基于多体动力学系统软件UM建立了考虑桥梁桩-土效应的车辆-桥梁动力相互作用模型如图1所示。

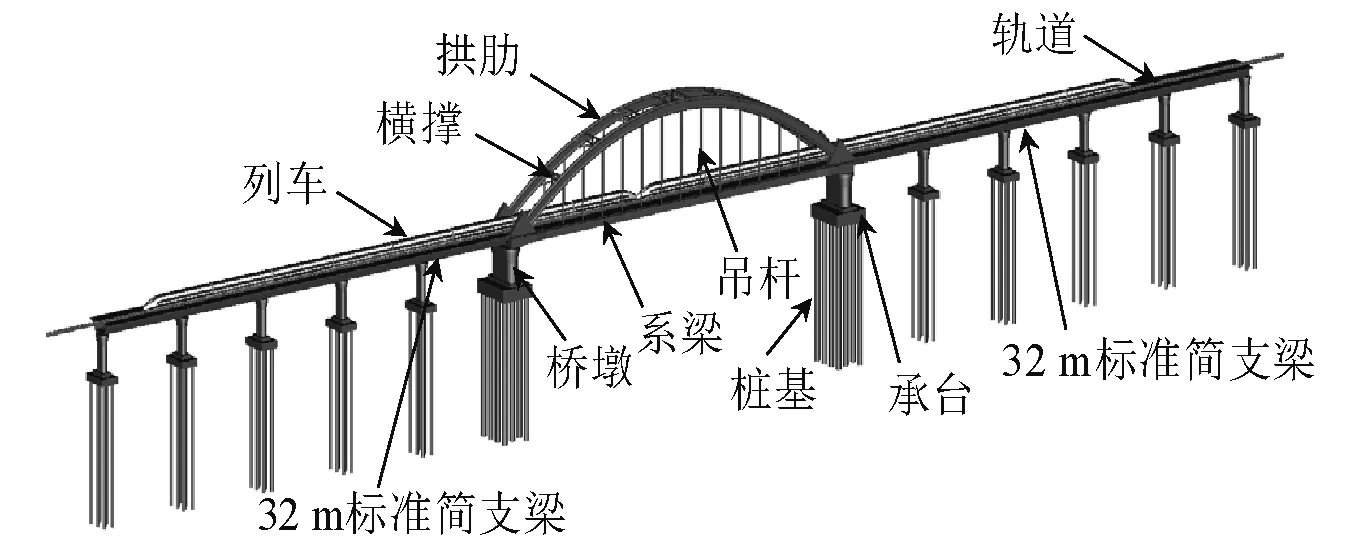
图1 车辆-桥梁动力相互作用分析模型Fig.1 The analysis model of vehicle-bridge dynamic interaction

为了方便计算轮轨力，将钢轨简化为连续弹性支撑的弹簧-阻尼系统，不考虑钢轨质量，但考虑轮轨的完整型面信息，以便计算法向力与蠕滑力。当车辆行驶在桥上时，轮轨垂向力、横向力计算由式(5)计算[11]

(5)

式中:kry,krz分别为钢轨与桥梁组成的系统中横向、垂向刚度；cry,crz分别为钢轨与桥梁组成的系统中横向、垂向阻尼；Δyr,Δzr分别为考虑钢轨、轨道不平顺、桥梁弹性变形的横向、垂向位移，该数值及一阶导数大小取决于车辆行驶的位置，若车辆未行驶上桥梁，则式中一阶导数为0。

由式(5)计算得到车辆行驶在桥上某时刻时的轮轨力，即为式(1)车辆系统、式(2)桥梁系统右端项的外荷载。通过判断车轮作用于桥上位置信息，将车辆作用于桥的垂向力、横向力按照静力等效原则转化到车轮对应下方桥梁结构的节点上，实现力的传递。因此对于式(1)、式(2)构成的方程组可在每个时间步内通过两个方程的迭代，得到满足其运动状态和作用力关系的解。

1.5 基于车-桥耦合分析模型的冲击系数计算

对于高速铁路桥梁，往往刚度是控制列车运行平稳性和安全性的重要指标，因此在车-桥耦合振动系统中，通过求解列车在一定运行条件下(运行速度、轨道不平顺)的冲击响应，获得桥梁控制截面(或结构模型关键结点)的动挠度波形轨迹，由式(6)得到冲击系数

(6)

式中：δd max为桥梁控制截面在列车作用下的挠度波形最大值；δs max为桥梁控制截面在列车作用下的挠度波形中心轨迹线的顶点值。

2 铁路钢管混凝系杆拱桥冲击系数分析

2.1 工程概况

某客运专线跨高速公路主桥为钢管混凝土系杆拱桥，计算跨径为136 m，引桥为32 m简支梁桥。系杆拱桥的系梁为单箱双室截面，拱肋采用哑铃型截面，矢跨比1/5，两拱肋之间共设置七道横撑。系梁为C55混凝土，拱肋采用Q345qD钢材，上、下拱管内为C50自密实补偿收缩混凝土。拱肋与系梁间共设置13组吊杆，采用高强低松弛钢绞线，设计强度1 860 MPa。桥墩为圆端形截面桥墩，墩高10 m，采用C35混凝土，承台及桩基采用C40混凝土。系杆拱桥截面及立面图如图2所示。

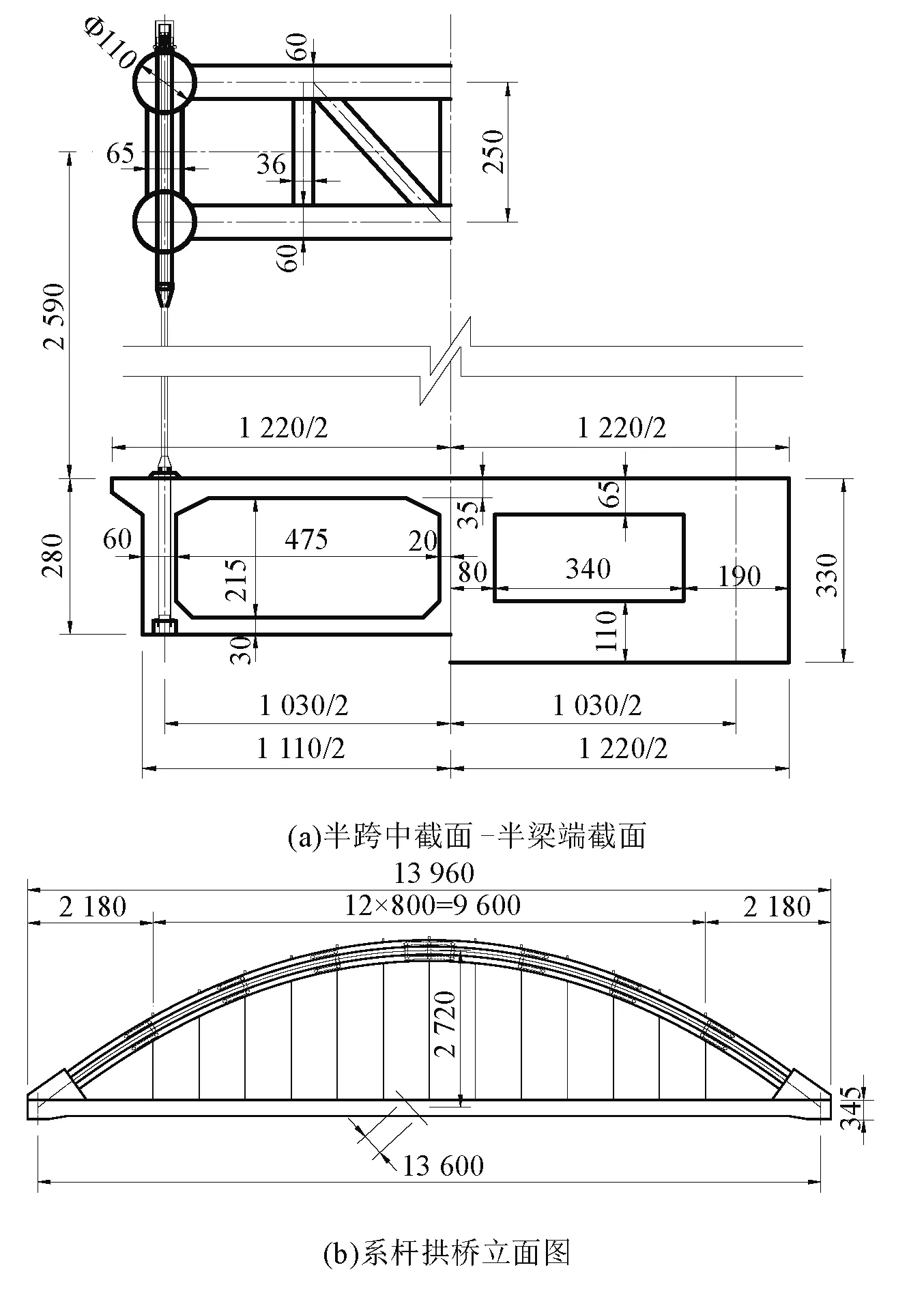
图2 桥梁立面及截面尺寸(cm)Fig.2 The physical dimension and section size of bridge (cm)

2.2 分析模型建立与验证

采用前述理论，采用多体系统动力学软件Universal Mechanism建立16编组高速动车组模型，编组形式为“动+拖+拖+动+动+拖+拖+动+动+拖+拖+动+动+拖+拖+动”，共计800个自由度，车轮踏面为LMA踏面，钢轨为CHN 60型面。车辆满员工况考虑为75 kg/人，其中头车按76人计算，中间车按100人计算。车辆运行最高速度依据规范按设计速度1.2倍考虑，故取速度区间为50～300 km/h，按每2 km/h一个速度等级变化，共计126个速度等级。

采用有限元软件ANSYS建立钢管混凝土系杆拱桥有限元模型，其中拱肋、系梁、拱肋横撑、桥墩采用beam单元模拟，吊杆采用link单元模拟，其中钢管混凝土采用组合截面原理等效为同一材料梁截面单元。桥面二期荷载包括轨道结构、人行道、防水层等重量，设计取值131 kN/m，采用mass单元模拟。全桥共建立单元1 906个，节点1 473个。桥梁支座按照设计类型，通过梁体与桥墩的结点同位移实现墩梁位移约束。采用基于“m”法的弹簧-阻尼力元模拟承台、群桩桩基与桩周土体的相互作用。

轨道不平顺作为车辆运动的主要激励来源，是引起车辆和线、桥、隧等结构物产生振动或破坏的重要原因[12]，本文采用兰(州)-新(疆)客运专线实测不平顺，该线路设计速度250 km/h，选择不同里程的30条不平顺样本作为激励，其中某条不平顺样本曲线如图3所示。

图3 实测轨道不平顺样本曲线Fig.3 The measured sample curve of railway irregularity

为了验证所建立车辆模型的正确性与可靠性，选取某线路实测不平顺作为激励样本，通过本文建立列车的车体垂向加速度与综合检车列车通过该不平顺线路时现场实测数据进行对比，时域与频域如图4(a)、图(b)所示。

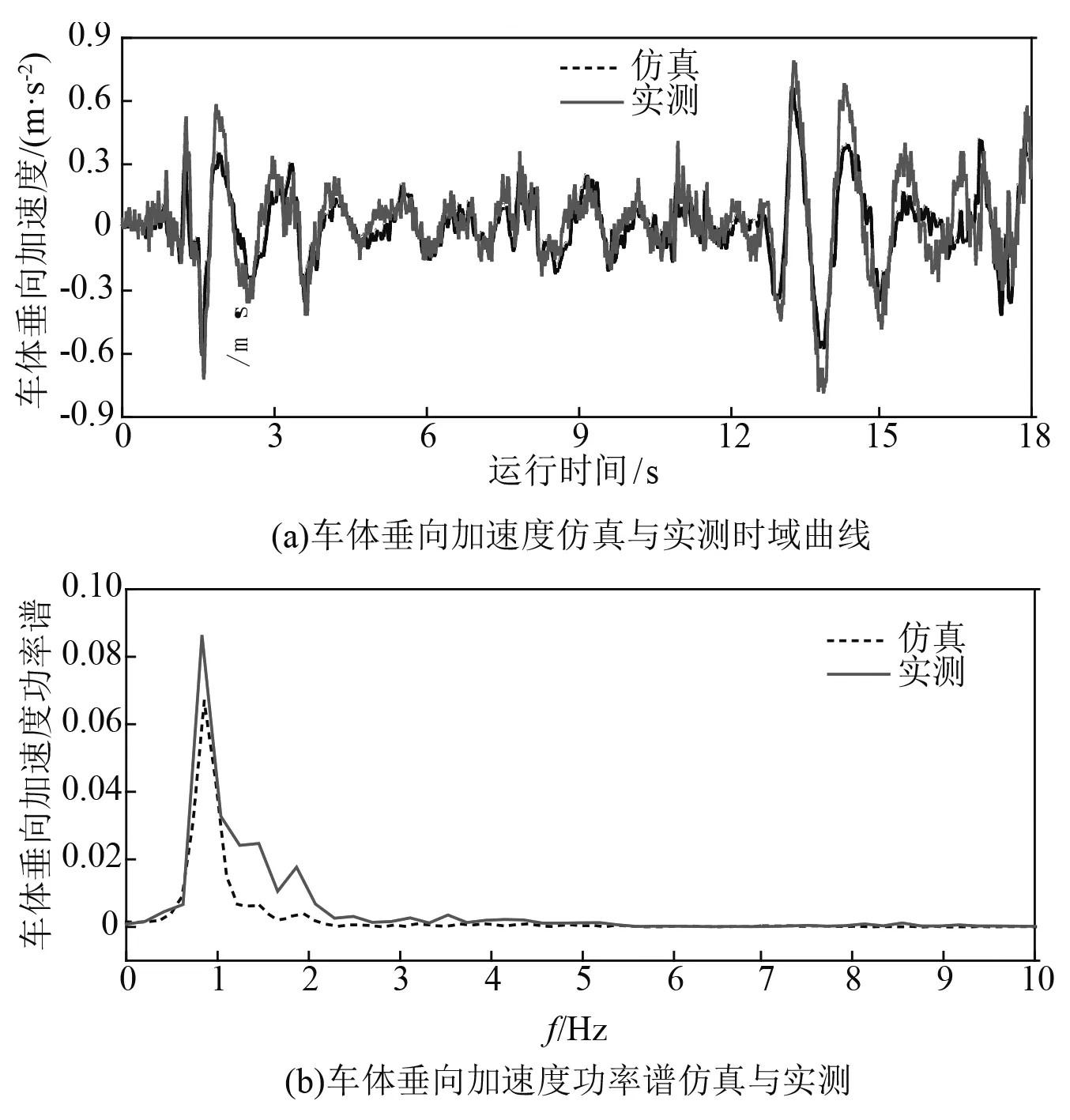
图4 车体垂向加速度仿真与实测对比Fig.4 The comparison between simulation and measurement in vertical acceleration of car body

由图4可知，数值仿真与实测结果时域曲线基本吻合，频域主频与实测一致，充分验证了软件的可靠性及仿真模型的正确性，因此本文建立的车辆模型可以作为系杆拱桥冲击系数研究的车辆模型。

2.3 系杆拱桥的冲击系数分析

依据前述不同速度、不同随机不平顺激励，共有7 560种计算工况。计算7 560种工况下系杆拱桥跨中处系梁、吊杆、拱肋的冲击系数并绘图，如图5所示。

由图5可知，对本算例而言冲击系数有如下特点：

图5 速度变化对系杆拱桥冲击系数φ的影响Fig.5 The influence of velocity variation on impact coefficient of tied-arch bridge

(1)系杆拱桥共振速度为134 km/h，这与文献[13]提供临界速度计算公式的计算结果相一致，因此行车时应避开此速度行车。

(2)当行车速度小于100 km/h时系梁与吊杆冲击系数较小，介于1.00～1.01；在速度小于第一临界速度(134 km/h)时，系梁、吊杆、拱肋冲击系数随速度增大呈现指数型增大，当大于第一临界速度后，基本在某一带状区域内波动；相比其他车速，临界车速下不同轨道不平顺冲击产生的动力系数离散程度最大，系梁、吊杆、拱肋冲击系数波动范围分别介于1.03～1.06,1.02～1.05,1.03～1.07，因此在桥上铺设线路时应尽可能保持轨道的平顺性，从而减小运营阶段车辆荷载对桥梁结构的冲击。

(3)对系杆拱桥各构件冲击系数由大到小依次为拱肋、系梁、吊杆，因此该类型结构的设计冲击系数应分构件类型给出。

2.4 系杆拱桥冲击系数统计分析

冲击系数是诸多因素随机组合产生动力效应的一个综合性系数，为了能够得到一个统一的数值来描述该系数，将系杆拱桥冲击系数采用连续随机变量概率模型进行研究，进而得到冲击系数随机变量统计规律。

依据数理统计学理论，分别将系杆拱桥系梁、吊杆、拱肋的7 560个样本点按从小到大依次排列，首先剔除小于1.001的数据，再依据统计学中|Xi-μ|≤2σ原则剔除样本中的异常值。

通过上述处理后的数据，再绘制得到系梁、吊杆、拱肋冲击系数样本点的经验概率分布图，可知3种分布形式符合极值Ⅰ型分布函数样式。依据统计推断理论中假设检验方法，以及柯尔莫哥洛夫拟合优度检验，得到系杆拱桥系梁、吊杆、拱肋冲击系数均不拒绝极值Ⅰ型分布。各冲击系数x的概率分布函数及统计参数如表2所示。

表2 冲击系数的概率分布函数及统计参数Tab.2 Probability distribution function and statistical parameters of impact factor

依据表2中冲击系数分布函数，可计算得某一分位点时的冲击系数。取保证率为95%(即置信度为0.05)的值作为系杆拱桥冲击系数，计算系杆拱桥系梁、吊杆、拱肋置信度为0.05的冲击系数值分别为：1.05,1.04,1.08。

2.5 系杆拱桥冲击系数拟合曲线

将每个速度下拱桥系梁、吊杆、拱肋冲击系数样本点进行从小到大排列，并剔除小于1.001及异常值，通过矩法估计得到每个速度下冲击系数拟合分布函数。用最小二乘法原理将置信度为0.05的冲击系数与速度进行回归分析，以函数拟合优度R2作为指标进行评价，得到满足置信度要求的的函数分布图，如图6所示。

由图6可知，尽管采用回归曲线反映了冲击系数与速度的函数关系，但还有部分样本点落在回归曲线之外。因此为了使得回归曲线能够包含所有样本点，将回归曲线外移，得到包含所有样本点的系杆拱桥置信度为0.05的冲击系数拟合曲线:

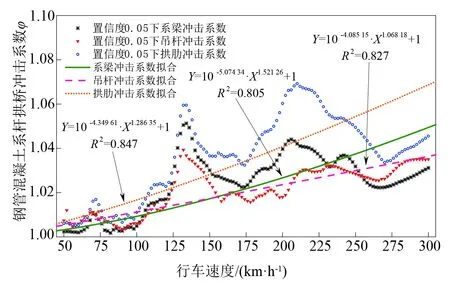
图6 冲击系数φ与速度的关系Fig.6 The relationship between impact factor and velocity

(1)系梁冲击系数与速度的函数关系为

φ=10-5.074 34·v1.521 26+1.036 8

(7)

(2)吊杆冲击系数与速度的函数关系为

φ=10-4.085 15·v1.068 18+1.024 2

(8)

(3)拱肋冲击系数与速度的函数关系为

φ=10-4.349 61·v1.286 35+1.035 6

(9)

式中，速度v单位为km。

对本算例而言，取速度v为设计速度250 km/h，通过式(7)～式(9)计算该冲击系数，并与按置信度0.05时冲击系数取值，以及车-桥耦合计算样本最大值对比，结果如表3所示。

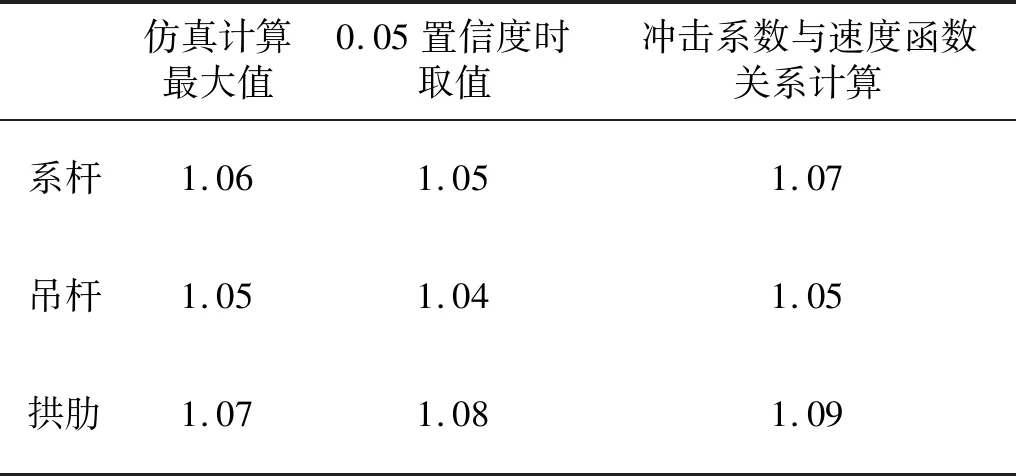
表3 冲击系数φ对比Tab.3 Comparison of several calculated impact factor φ

由表3可知，通过函数式(7)～式(9)计算冲击系数相比车-桥耦合仿真计算结果更安全。由于置信度0.05时的冲击系数取值综合考虑了不同速度、不同不平顺下冲击系数的离散性，其结果更合理。

3 结 论

本文以某设计速度250 km/h的高速铁路客运专线的一座计算跨径为136 m的钢管混凝土系杆拱桥为例，建立了考虑桩-土作用效应的列车-桥梁动力相互作用模型，研究了不同不平顺样本下系杆拱桥系梁、吊杆、拱肋冲击系数随车速的变化规律，主要结论如下：

(1)系杆拱桥存在临界车速，在小于临界车速时冲击系数随速度增大呈指数增大，大于临界车速后在一带状范围类上下波动。当车速小于100 km/h时系梁、吊杆、拱肋冲击系数均接近于1.0。

(2)系杆拱桥主要受力构件的冲击系数存在差异，其拱肋冲击系数最大，其次为系梁，吊杆冲击系数最小，设计时应考虑不同构件冲击系数的差异。

(3)经假设检验理论统计分析，系梁、吊杆、拱肋冲击系数不拒绝极值Ⅰ型分布。取保证率为95%的值作为系杆拱桥冲击系数，本桥系梁、吊杆、拱肋冲击系数分别为1.05，1.04，1.08，均大于现有规范的取值。

(4)对于高速铁路系杆拱桥，现有规范对冲击系数不仅没有考虑各构件的差异，同时取值偏小。因此在进行大跨度系杆拱桥设计时，冲击系数取值应考虑必要的放大，以利于桥梁安全。