先简支后连续梁桥施工线形控制技术研究
张志高
(中铁十八局集团第五工程有限公司,天津 300222)
1 引言
为提高施工质量及其安全性,确保桥梁成桥之后的线形满足设计要求,必须对其进行施工监控。对于先简支后连续梁而言,因其多采用节段预制的方式进行施工,在某一跨完成预制箱梁节段的拼装之后,即基本确定了其余各跨的线形[1],因此对于先简支后连续梁而言必须对其节段预制时的线形进行施工控制。
2 工程概况
本次研究所基于的背景桥梁结构要点为:主梁采用的截面形式为等截面单箱单室截面,3m的主梁高度,箱梁顶板以及底板的宽度分别为16m和7m;厚度分别为26cm和25cm。箱梁纵向以及横向均施加预应力,采用15.2mm直径的钢绞线以及塑料波纹管作为成孔管道。
中部横隔梁需进行现浇,箱梁其余部位在工厂预制完成,然后运送至现场进行吊装施工。以预应力张拉的方式使各个分段预制梁块形成整体后,采取连续段横隔梁现浇方式,箱梁完成从简支到连续的体系转换。在简支状态下,箱梁一期荷载以及施工荷载均由体内预应力提供;在连续状态下,二期荷载以及活载均由体外预应力张拉提供。
通过有限元软件Midas/Civil建立该桥梁模型,如图1所示,并对其进行仿真分析。通过仿真分析获得桥梁在施工阶段的受力状态,以获取其内力及变形数据,从而为桥梁施工控制提供依据。基于篇幅所限,本文仅列出部分模型数据。

图1 一联建模图(以116#-122#墩为例)
3 仿真数据分析
虽然通过仿真分析可以得到较为精确的施工预拱度,但桥梁实际施工时所受影响较多,如气候温度以及时间等。鉴于其复杂性,为进一步确保桥梁施工的安全性,本文对该桥梁开展了单梁静载试验。
本次静载试验加载时以纵向跨中截面最不利弯矩处采用沙袋直接进行加载,布载方案为跨径的一半。所得结果如图2所示。

图2 各级加载挠度值
从图中可知,桥梁的竖向挠度在跨中存在46mm的最大值,可知其处于规范L/600的允许范围内。
静载试验下各截面测点所测得的应变值如图3所示。
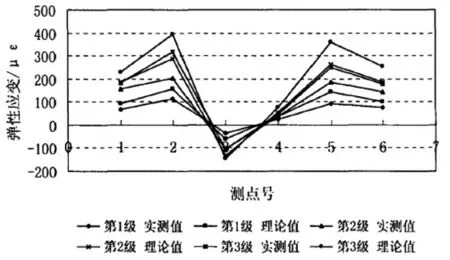
图3 各级加载应变图
从相关规范可知,桥梁校验系数应在0.9-0.5的范围内,其实际值有着0.8的最大值,以及0.63的最小值,可知该桥梁的应变校验系数满足要求。对其相对残余变位进行计算可知其有着0.19的最大值,满足0.2容许值的要求。
3.1 汽车活载计算
该桥梁采用的汽车荷载等级为公路-Ⅰ级,为考虑最不利状态,本文考虑了放大系数1.3。仿真数据如图4所示。

图4 汽车活载挠度/mm
从图4中可知,桥梁在汽车活载下具有-9.678mm的最大挠度值,对结构线形不会造成影响。
限于篇幅,本文仅列出部分数据。汽车活载弯矩包络如图5所示,从汽车活载下的弯矩仿真结果可知:在汽车活载作用下,桥梁有着2.06e4KN/m-1.75e4KN/m的最大弯矩值,桥梁结构保持在安全状态,满足要求。
图5 汽车活载弯矩包络图
3.2 温度作用计算
(1)系统温度作用
为对桥梁的内力以及变形开展更进一步的研究,本文基于规范要求,选取在20℃的基准温度,34℃的高温以及-10℃的低温环境下,分析温度与桥梁内力和变形之间的关系[2-3]。所得结果如图6所示。

图6 系统降温挠度曲线图(单位:mm)
从仿真结果可知,桥梁在体系温差以及结构约束环境下,有44.955mm的最大位移值出现在主梁段的伸缩缝位置,而其在纵向则产生了0.086mm的最大挠度。
(2)梯度温度作用

图7 温度梯度作用下的结构挠度曲线图(单位:mm)
从图7的仿真结果可知,箱梁结构截面在因日照等因素影响而产生的温度梯度作用下,仅有3.040mm的最大变形值以及2.16mpa的次用力,两者均满足设计要求。
3.3 支座沉降计算
本文以10mm的最大沉降量对单个支座进行计算,所得结果如图8所示。
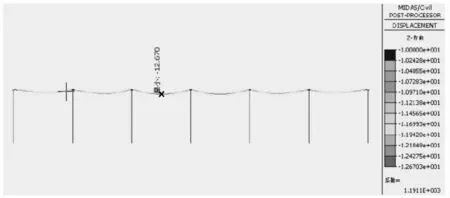
图8 支座沉降变形包络图(单位:mm)
从结果可知,主梁上缘内力在支座沉降时有着0.796mpa的最大值,下缘内力在支座沉降时有着1.192mpa的最大值,此时桥梁结构仍处于安全状态,桥梁结构有着-12.669mm的最大挠度值。
3.4 荷载组合验算
本文主要考虑了两种荷载工况,两种工况仅在温度作用有所区别,即恒载+活载+支座不均匀沉降+整体升温(工况一)/整体降温(工况二)+梯度正温差(工况一)/梯度负温差(工况二)。两种荷载工况的仿真结果如图9所示。

图9 荷载组合计算结果
从仿真结果可看出,在两种工况下,多数截面都保持在全截面受压状态,满足全预应力设计要求;在工况二下,有较小的拉应力出现在桥墩墩顶下缘截面,因混凝土的收缩徐变作用,导致该位置表现出受压的应力状态;此外,在本次模拟过程中,因未对支座弯矩削峰效应进行考虑,因此该位置较小的拉应力仍满足设计要求。
3.5 仿真计算结果
将各个阶段的挠度最大值归纳如表1所示。

表1 桥梁挠度变形与应力值

续表
从上表可看出,箱梁截面在各种荷载作用下均保持在全截面受压状态,并且桥梁所受最大应力满足设计要求,即桥梁结构处于安全状态,满足全预应力要求;基于桥梁预拱度设置要求,若桥梁在其自重以及活载作用下产生的最大挠度小于L/1600时,可不设置预拱度[4]。该桥梁计算跨径为50m,有着31.25mm的容许最大竖向挠度。从表2可知,桥梁在各荷载下所产生的挠度满足要求。故该桥无需设置预拱度。
4 施工控制
本文以上述有限元模拟结果为依据,采用短线法进行实例计算以及误差分析。该桥梁现场预制厂有两条生产线,分别位于南北方,具体如图10所示。本文将以中跨对象研究匹配坐标和误差分析方法,以对桥梁线形进行控制。基于该桥梁仅需以设计线形进行预制施工的特点,本文将以短线法对其预制线形进行计算分析,以满足线形控制的要求。

图10 预制厂布置示意图
从上图可知,有六个测量塔设置在南北生产线的中部位置,主要用以开展测量放样以及校核等工作。从B5-0中间段开始进行一整跨梁的预制工作, (因该梁段为标准件,故无需进行匹配工作),以该梁段为起点,分别朝两边开展匹配工作。
4.1 匹配计算
基于上述仿真结果,本文以110#-120#墩间的三个梁段(编号:A,B,C)为研究对象进行匹配坐标的计算以及误差修正的探讨。
为提高施工效率,选取B5-0的待浇筑段为B6-2,并将其作为B5-2的匹配梁。以B5-0最中间段开始进行各跨梁段的预制。因首段单元梁为B5-0,因此无需对其进行匹配。故其线形控制的质量将会对接下来各个梁段的线形造成影响。故在每次预制之前需对B5-0梁段台座的跑位情况进行监测,以控制其误差处于设计要求之内。
待A号梁段预制完成之后(在梁段预制时,需在混凝土浇筑时将测量点埋设到位,测点布置如图11所示,需对测点坐标进行测量,并计算出其大地坐标系,所得结果如表2所示。

图11 测点埋设位置示意图(单位:cm)

表2 梁段A整体坐标值与局部坐标值(单位:m)
表中竣工初始坐标即浇筑完并养护完梁段A之后测量所得坐标。上表坐标值即梁段A在自身局部坐标系下的坐标。在开始匹配梁段B之前,必须对梁段A的匹配坐标进行计算。梁段A的匹配坐标可通过软件Auto-CAD以建立局部坐标系的方式,计算出梁段B的局部坐标下的两端B的整体坐标,所得结果如表3所示。

表3 梁段A匹配坐标计算表(单位:m)
取得匹配坐标之后,即可采用全站仪对其进行监控,并通过千斤顶进行微调,将梁段A调整至匹配坐标处并对台座进行固定,之后即可开展梁段B的浇筑。
4.2 匹配误差修正
假定待浇筑段为N号块。将N号块制作误差作为N-1号块匹配误差的转移对象。故对于N+1号块的匹配需通过调整N号块的方式实现。即通过调整N+1号块的匹配过程来调整N号块的制作误差。在制作N+1号块时可以负数的实际误差做为修正值,从而满足调整要求。如图12所示。

图12 误差调整示意图
上图A表示各梁段理论线形。假定预制1号块时出现角度误差α角,此时在2号节段的拼装会受到1号节段的误差的影响,如图C所示;上个节段传递下来的误差,降低了2号节段高程,为对该误差进行修正,可在下一节段施加相应的β转角以进行抵消,如图D所示。此时在预制4号节段时梁体线形已回归设计线形,即角度误差α已经通过3号节段的坐标匹配抵消掉。
5 结语
通过放置计算结果可知,该桥梁在荷载组合作用下的最大变形仍满足设计要求,因此可知,在该梁段施工时并不需要施加预拱度,即在预制箱梁时可直接以设计线形开展。基于计算结果,本文采用短线法对其进行计算分析,并针对匹配坐标误差进行修正,基于现场桥梁拼装后的线形而言,桥梁线形控制满足要求。

