基于马尔可夫决策过程的算法研究

肖 铮

（四川工商职业技术学院 信息工程系，成都611830）

0 引言

5G 网络系统中，采用了终端直通（Device-to-Device，D2D）技术直接通信，D2D 技术是目前最具前景的5G 技术。所谓D2D 通信技术，就是指两个对等用户进行直接通信，而不需要利用基站转发的一种新型通信方式。[1]在由D2D 用户组成的网络中，每一个用户都能发送并且接收通信信号，同时还具有路由功能。如果D2D 用户之间的距离很近，而两者距离基站很远，那么选用直接通信的方式更好。上述情况只是一个简单的特例，有时因为网络状态等因素，反而选择理论上不可取的方式对解决实际问题更加有利。因此，需要寻求一种通用的、能适应大部分情况的方法，同时需要对实际问题进行建模，确定一种通用的模式选择规则。本文将D2D 模式选择与马尔可夫决策过程（Markov decision process，MDP）[2]相结合，提出了一个解决模式选择问题的新思路：基于马尔可夫决策过程的算法研究。

1 马尔可夫决策过程模型

1.1 信道模型

如果D2D 用户采用的是复用蜂窝资源的通信方式，网络内部就会产生新的干扰，每一个接收用户都会收到来自复用同一频带资源的其他用户的干扰信号，基站也会受到影响。采用平坦瑞利衰落信道模型，接收端信号幅度满足瑞利分布。瑞利分布是一个平稳的窄带高斯过程，它的均值是0，方差是σ2。[3]在该信道模型中，假设接收机会受到一个加性高斯白噪声（AWGN）的影响。AWGN 是无线信道中最基本的噪声干扰模式，其幅度服从高斯分布（零均值，方差为N0）。在该模型下，可以得到信噪比SINR。[4]

SINR代表的是设备信号和噪声的比值，SINR越大，代表信号的质量越好。公式（1）中的Preceiver是接收设备接收到的功率，I是接收设备受到的干扰，N0 是接收设备受到的噪声，Pt是设备发送功率。一般情况下，蜂窝用户和D2D 用户的发送功率并不一致，前者的发送功率相对更高一些。实际情况下，为了最大化网络吞吐量，还需要进行功率分配，使发送功率按一定的规则进行设置，由于此部分内容不属于本研究的范畴，所以这里不再赘述。为了使计算更加方便，默认在任何情况下，用户的发送功率一致为PDUE，不做发送功率大小的区分；dij代表信号发送设备i到信号接收设备j的距离；Hij指的是信道系数；α 是路径损耗系数，代表信号在空间里传播时将会产生的损耗，它由两方面的因素决定，一是信道本身的传播性质，二是发送功率的辐射效应。根据标准路径损耗传播模型，一般情况下，α＞2。

如果期望最终能获得最大化的网络总体信道容量Csystem，需要进一步计算整个系统的总体信道容量。在该模型下，网络结构中包含了一个蜂窝用户和两对D2D 用户，所以Csystem是三个用户信道容量相加后的结果，如公式（2）所示。

公式（3）是信道容量的通用计算公式，BW指的是系统资源带宽，SINR指的是公式（1）中计算出来的相应信噪比。

1.2 马尔可夫模型

MDP 可以从五个要素着手来分析：决策时刻和周期，状态，行动集合，转移概率，报酬。每一次做决策的时间点集合用T来表示，而对应的系统状态集合用S来表示，行动的集合采用字符A来表示。在某一个时间点，假设存在一个状态i∈S，那么，在这个状态的可用行动集A（i）中挑选出一个行动a 并执行之后，可以得到一个报酬r（i，a），同时，下一个时刻的系统状态将根据转移概率分布函数p（*|i，a）决定。然后，在下一时刻又需要进行另一次行动的选择。最后，将所有时间点的行动组合起来，就可以获得一个决策序列，即所做选择的集合。每一次行动选择除了可以带来一份及时报酬之外，还会对将来产生影响，产生额外的报酬，如图1 所示。

图1 决策过程图

1.3 马尔可夫决策模型的算法

采用基于动态规划的期望报酬值向后递归的迭代算法来计算D2D 模式选择问题下的马尔可夫决策模型最优值问题。[5]算法中，ft*代表的是时刻t的最优策略，而π 就是策略序列集合。在N时刻，由于前N个周期0，1，…，N-1 的历史情况已被确定，所以此时决策者没有其他的决策可选，是固定的值。集合一般被定义为最优行动集合。这种向后递归算法体现了一种最优化原理的思想。最优策略的性质是：不管从哪一个初始状态开始出发，以及无论采取了怎样的初始行动，对下一个决策时刻来说，剩下的决策规则组成的策略就是最佳策略。[6]该算法步骤如下：

步骤一：令t=N且对一切it∈S，

步骤二：若t=0，则就是最佳的MDP 策略，同时就是最优的值函数，那么算法停止。否则，令t-1⇒t后，再进行步骤三。

步骤三：对一切it∈S，计算

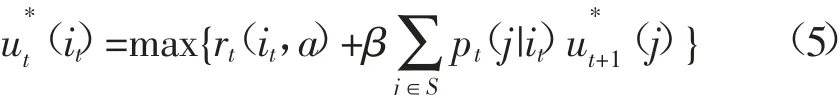
记集合

步骤四返回到步骤二。

由于行动集合A*是有限集合，该马氏策略的最优解一定存在，并且可以由上述算法得到最终的每一个决策时刻下的行动选择，将之组合起来就是要求的模式选择的策略序列，即策略Policy。通过查找Policy 矩阵，可以准确地知道某一决策时刻（时隙），在系统处于某种状态时，两个D2D对应该做出的模式选择。同时，当前模式也可以得到一个期望报酬最优值V。算法的流程如图2所示。

1.4 仿真实验

结合网络结构模型，设置的参数见表1。表1中的距离参数是初始情况下的取值，具体情况可能会发生一些改变。为了简化模型，将信道系数Hij取值为1。同时，需要注意的是功率以及噪声的单位并不统一，在实际计算过程中应当进行单位的转换。

图2 向后递归算法流程图

表1 仿真参数表

2 实验结果

利用有限阶段向后递归迭代算法将之联系起来，组合成一个完整的MDP 问题，在Matlab 平台上进行建模仿真，并适当地改变一些参数，观察网络吞吐量的变化情况。具体实验结果如图3-图5所示。

图3 阶数N 对V 的影响变化趋势图

在图3 中，R1=300m，r1=10m，r2=10m。由于在任一状态下，它的最优值变化趋势是保持一致的，且一般情况下，信道状态良好的可能性会更高一点，同时也更希望了解信道状态良好时的情况。所以为了简化图像，选取其中的两个状态（1111 和1110）作为代表。

图4 D2D 对之间距离对V 的影响变化趋势图

图4 中，R1=300m，同步改变两对D2D 对之间的距离r1 和r2（运动方向均与x 轴的夹角为0 度，且运动方向保持不变）。通过观察可以发现，从变化趋势上来说，随着D2D 对距离的增大，在期望报酬的具体数值上，当两个D2D 对之间的距离同步变化时，最终的期望报酬值变化会更剧烈，变化范围也更大。由此可以类推，当系统中出现多个D2D 对，并且同时处于运动状态时，系统的信道容量有可能出现极端情况，这也是在将来的研究中需要考虑的问题。

在图5 中，R1=300m，r2=10m，改变第一对D2D 对之间的距离r1，同时取阶数N=100，时隙数为500。通过仿真可以看到距离的增大必定会导致信道容量的减小，这是由于接收到的信号变弱导致的。同时，可以清晰地看到基于MDP 和基于信道容量这两种方法的结果，在最大化网络吞吐量这一性能上存在一定的优劣，基于MDP 的模式选择显然能获得更大的系统信道容量。经过计算得知，基于MDP 的方法比基于信道容量的方法平均高出6Mbps 左右信道容量，而差距最大的地方（距离大约为51m）基于MDP 的方法几乎高出了7.1Mbps 的信道容量，数值非常可观。

图5 基于不同模式选择方法的系统总吞吐量比较

3 结果分析

在基于信道容量等方法的基础上，将网络的信道状态纳入了考虑范围，利用MDP 来分析模式选择问题，并观察了距离等因素对吞吐量的影响，目的是寻求到能获取最大信道容量的一种模式选择方法。实验结果表明，马尔可夫决策过程算法在实现最大化网络总吞吐量这一目标上，可以达到更好的效果。

4 结语

利用动态规划思想中的迭代算法来解决网络吞吐量问题，在计算复杂度下，得出一个与时间有关的决策序列。经过最后的多个时隙下的仿真比较证实，在最优化网络吞吐量方面，本研究的基于MDP 的模式选择方法确实具有一定的优势。在接下来的工作中，希望能够找到更为合理的方法，进一步提高算法的决策效果。