具有Crowley-M artin功能反应函数的非自治捕食-食饵系统的动力学行为*
艾孜海尔·哈力克,艾合麦提·麦麦提阿吉
(新疆大学 数学与系统科学学院,新疆 乌鲁木齐830046)
0 引言
在现实世界中,两个种群之间有着多种相互作用.其中捕食-食饵关系是最常见和最原始的生态相互作用之一.值得注意的是,数学生态学的整个领域都是从种群间的捕食-食饵相互作用的种群动力学开始的,例如Lotka[1]和Volterra[2]的工作.近年来国内外学者对种群捕食者-食饵动力系统进行了广泛的研究[1-8],并且取得了很多研究结果.在描述捕食者及其食饵的动态相互作用时,大多数种群捕食-食饵动力系统研究总是利用功能反应函数(比例依赖函数)来描述捕食者的捕食率和转化率[3-8].例如,文献[5]研究了以下具有Crowley-Martin功能反应函数的两种群自治捕食-食饵系统
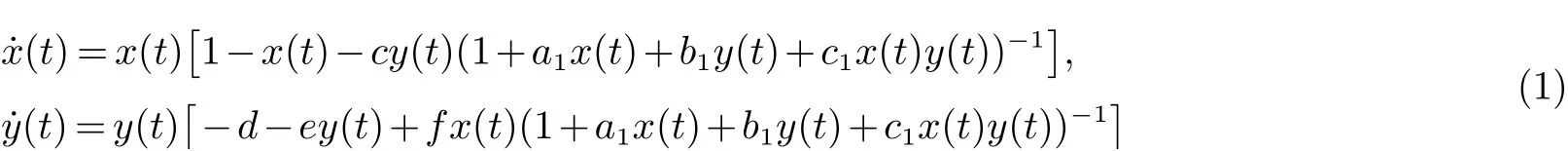
的持久性、非持久性以及几个正平衡点的局部和全局渐近稳定性.其中x(t)和y(t)分别是食饵种群和捕食者种群x和y在时刻t的密度;在系统(1)中cy(t)(1+a1x(t)+b1y(t)+c1x(t)y(t))-1和fx(t)(1+a1x(t)+b1y(t)+c1x(t)y(t))-1表示Crowley-Martin功能反应函数,并且作者在文献[1]中用这两个功能反应函数来描述捕食者和食饵之间的捕食-食饵关系.值得注意的是,Crowley-Martin功能反应与Beddington-DeAngelis功能反应的主要区别是Crowley-Martin功能反应是依赖于捕食者.文献[5]指出,依赖于捕食者的功能性反应可以更好地描述一系列捕食者-食饵数量上的捕食行为.
另一方面,在自然界中种群的栖息地环境都会随着时间的变化而发生变化,这导致这些种群的生长特征发生变化.所以建立种群动力学模型时应该考虑非自治模型,这将与真正的生态系统更加相似.因此,研究非自治种群捕食-食饵动力学模型很有价值.本文结合以上的研究工作和模型(1),研究下面的具有Crowley-Martin功能反应函数的两种群非自治捕食-食饵系统

通过应用微分方程比较原理和Lyapunov函数方法研究系统(2)的有界性、持久性、灭绝性、正周期解的存在性以及全局吸引性等动力学行为.
1 预备知识
在本文中,假设系统(2)满足下面的初始条件:
(H1) a1(t),b1(t),c1(t),d(t),c(t),f(t)和e(t)是区间[0,+∞)上有界,连续的正函数;
(H2) a1(t),b1(t),c1(t),d(t),c(t),f(t)和e(t)是ω-周期正连续函数.
为了叙述方便,对任意在区间[0,+∞)上连续的函数f(t),我们用下面的记号

此外,我们还将用到如下一些定义和引理.
定义1[8]我们称系统(2)是持久的,如果存在正的常数mi,Mi(i=1,2)和T*使得系统(2)的每个正解(x(t),y(t))对于任何给定初始条件Φ满足m1≤x(t)≤M1,m2≤y(t)≤M2,∀t≥T*,其中T*依赖于Φ.
定义2[9]称系统(2)是全局吸引的,如果系统(2)的任意的两个解(x(t),y(t))和(u(t),v(t))满足

引理1[10]考虑下面的方程


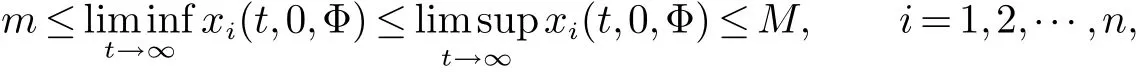
则下面一般形式的泛函微分方程

一定存在周期为ω的正周期解.其中x(t)∈Rn而F(t,xt)是n维连续实泛函,x(t,0,Φ)=(x1(t,0,Φ),x2(t,0,Φ),···,xn(t,0,Φ)).
引理3[11]设f是定义在[0,∞)上的一个非负函数使得在[0,∞)上可积,并且在[0,∞)上一致连续,则
2 有界性、持久性、灭绝性和正周期解的存在性
定理1 假设H1成立,则存在常数Mi>0(i=1,2),使得系统(2)的任一个正解(x(t),y(t))满足下面的条件

证明 设(x(t),y(t))是系统(2)满足初始条件(4)的任一个正解.首先,当t>0时由系统(2)第一个方程可以得到

考虑下面的辅助方程

由引理1可以得到

根据微分方程的比较原理,存在一个常数T0>0,使得当t>T0时x(t)≤M1.下一步,当t>0时由系统(2)第二个方程可以得到
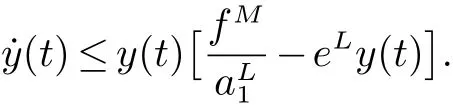
与上面方法类似,对y(t)存在一个常数T1>0,使得当t>T1时y(t)≤M2.其中
定理2 假设H1成立并且bM1>cL,R>0,则系统(2)是持久的.其中

证明 设(x(t),y(t))是系统(2)满足初始条件(4)的任一个正解.首先,当t>0时由系统(2)第一个方程可以得到

考虑下面的辅助方程

由引理1可以得到

根据微分方程的比较原理,存在一个常数T2>0,使得当t>T2时x(t)≥m1.下一步,当t>0时由系统(2)第二个方程可以得到

与上面的方法类似,存在一个常数T3>max{T0,T1,T2},使得当t>T3时y(t)≥m2.
由引理1的第二个结论,可以得到下面的推论.
推论1 假设H1成立并且则系统(2)中的捕食者种群y灭绝.
由引理2,可以得到下面的推论.
推论2 假设H2成立并且则系统(2)是持久的并且至少有一个正ω-周期解.
3 系统的全局吸引性
首先,为了方便我们记

其中


定理3 假设定理2的条件成立,且A>0,B>0,则系统(2)是全局吸引的.
证明 设(x(t),y(t))和(u(t),v(t))是系统(2)的任意两个正解.由系统(2)的持久性,存在常数T>0,mi>0,Mi>0(i=1,2)使得
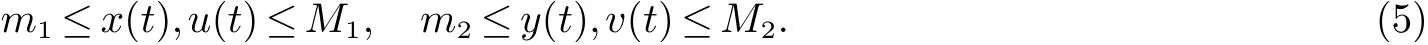
对一切t≥T成立.定义Liapunov函数

则沿着系统(2)计算V(t)的右上导数,得到

令C=min{A,B},则得到

在区间[T,t]上积分(6),我们得到

从而

由(5),(7)和(8)我们可以得到x(t),u(t)和y(t),v(t)的导数˙x(t),˙u(t)和˙y(t),˙v(t)在区间[T,+∞)上是有界的.从而|x(t)-y(t)|+|u(t)-v(t)|在区间[T,∞)上是一致连续的,由引理3我们得到

因此,
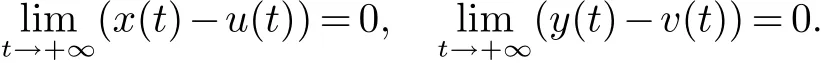
由推论2和定理3,我们有下面的结论.
推论3 假设推论2的条件成立,且A>0,B>0,则系统(2)有一个全局吸引的正ω-周期解.
4 结论
本文研究了具有Crowley-Martin功能反应函数的非自治捕食-食饵系统的动力学性质.首先运用不等式估计方法和微分方程的比较原理得到模型的有界性、持久性、灭绝性、正周期解的存在性.其次模型在持久的条件下构造适当的Lyapunov函数得到了模型的全局吸引性.本文中研究的模型和得到的结论推广了文献[5]的结果.

