Fixed-Time Synchronization of Coupled Memristive Complex-Valued Neural Networks*

FENGLiang,HU Cheng,YU Juan

(School of Mathematicsand System Sciences,Xinjiang University,Urumqi Xinjiang 830046,China)

Abstract: This paper investigates the fixed-time synchronization of coupled memristive complex-valued neural networks(MCNNs)with time-varying delay.Firstly,a complex-valued sign function is introduced to avoid the common separation technique and a new fixed-time stability theorem is established to improve the existing ones.Afterward,by proposing a discontinuous control scheme and applying differential inclusion theory,some criteria are derived to achieve fixed-time synchronization of master-salve coupled MCNNs.The developed control scheme here simplif ies the traditional design by excluding the linear part.Finally,anumerical exampleisgiven to validateof thetheoretical results.

Key words:complex value;coupled neural network;fixed-time synchronization;memristor

0 Introduction

Memristor was first proposed by Professor Chua in 1971[1]to describe the relationship between flux and charge.Since memristor can better simulatethemechanism of human brain memory and forgetting,many researchershavebeen motivated to introduce it into neural networks and a mass of memristive neural networks(MNNs)has been established.Nowadays,the study of dynamic behaviors of MNNs,such as stability[2]and synchronization[3],has attracted wide attention in various fields.

In recent years,complex-valued neuronshavebeen successfully applied in pattern recognition and nonlinear filtering in view of their greater computing power and information storage capabilities compared with real-valued neurons.Currently,someinteresting resultsaboutmemristivecomplex-valued neural networks(MCNNs)havebeen reported[4,5].In mostexisting theoretical results,complex-valued systems were separated into two real-valued systems and then the dynamic behaviors wereinvestigated by using thecommon analytical techniquefor real-valued neural networks(RNNs).Although thismethod is effective,it also leads to complex calculation in theoretical analysis and the failure to ref lect complex-valued features and superiorities.Therefore,it is of great signif icance to explore new methods to study MCNNs in theoretical analysis and practical applications.

Recently,fixed-time control has been vastly studied in various fields because of the faster convergence compared with traditional feedback control and the independence of convergence time on initial conditions in comparison with finite-time control.However,although thef ixed-timesynchronization of real-valued MNNshasbeen extensively studied[6,7],few scholarshaveexplored the fixed-time synchronization problem of MCNNsbecause of the theoretical difficulty.

Inspired by the discussion above,the purpose of this paper is to investigate the fixed-time synchronization of coupled complex-valued memristive neural networkswith time-varying delays.Firstly,to avoid separating thecoupled MCNNsinto two real-valued subsystems and designing two real-valued controllers in existing results[4,5],a complex-valued sign function and a new norm for complex-valued numbers are introduced.Secondly,a new fixed-time stability theorem is establishedto improve the existing result[8].Based on the developed theorem,a new fixed-time controller is proposed for MCNNs to improve the previouscontrol design[6,7]and some less conservative criteria are derived to realizef ixed-time synchronization.

1 Preliminaries and model description

Referring the MCNN model in[9],consider acomplex system coupled by N MCNNs,which can bedescribed asfollows

Lemma 5 Assume that V(x(t)):Rn→R+is a regular,positive def inite,radially unbounded function and x(t)is absolutely continuouson any compact subinterval of[0,+∞),if

where a∈R,0≤β＜1,θ＞1,and b,c arepositiveconstantssatisfying min{b,c}＞a,then V(x(t))=0 and x(t)=0 for any t≥T,and T isestimated by

Proof Let v(t)=V(x(t)),it has

Since0≤β＜1,θ＞1 and min{b,c}＞a,then˙v(t)≤av(t)-bvβ(t)-cvθ(t)=-Υ(v)≤0.

On theother hand,from(7),it has

where v0=v(0).

IfΨ0＞1,

Combining thesetwo cases,onehas

According to the finite-time stability theory in[14],v(t)=0,x(t)=0 for any t≥T,and T doesnot depend on the initial value.

2 Main Results

In thissection,weconsider fixed-time synchronization between system(1)and system(4)by designing adiscontinuous controller.

For any k=1,2,···,n,i=1,2,···,N,we introducethefollowing notations.

Theorem 1 Under Assumption 1,the controller in system(4)is designed by

By using Assumption 1,

According to Lemma 3,one can get

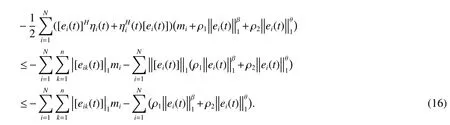
Substituting(12)-(16)into(11),from Lemma1 and condition(9),wecan obtain that

By(17)and Lemma 5,system(1)and system(4)can be synchronized under the control scheme(8)in a fixed time T0which isestimated by

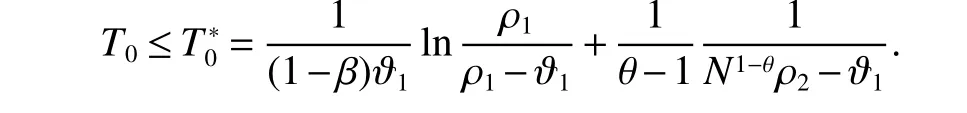
This completestheproof of Theorem 1.

When the nonlinear is reduced to linear case,that is,g(v)=Γv for v∈CnandΓ=diag{γ1,γ2,···,γn}withγk∈R in systems(1)and(4),thefollowing result iseasily obtained.

Corollary 1 Under Assumption 1 and the control law(8),if

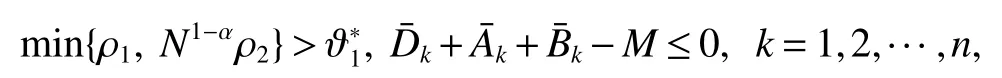
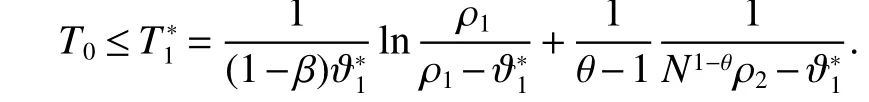
Remark 1 In Theorem 1,ifβ=0,theestimateof T0isreduced to thefollowing form

Remark 2 In the previous results[4,5]on dynamic behaviors of MCNNs,the separation method was utilized to obtain two real-valued subsystemsand themain resultswerederived by analyzing thesereduced real-valued models.Different from theseparation technique,thecomplex-valued sign function isintroduced in thispaper to directly design the complex-valued control scheme and construct Lyapunov function,and the theoretical analysisisf inished in the complex field.

Remark 3 In the most of results on fixed-time synchronization[6,7],the linear term about the errors is indispensable in the design of controllers.Unlike the common design,the control law given in this paper is simplif ied by excluding the linear part.In addition,Lemma 5 generalized the existing fixed-time stability into discontinuous system and improved the estimation of the settling time provided in[8].

3 Numerical simulations

In this section,a numerical example is given to verify the theoretical results.

Under those parameters,the chaotic attractors of the real part and the imaginary part for xi(t)in system(1)without the coupling are shown in Fig 1 and Fig 2,in which x1(0)=-2.18-1.09i and x2(0)=-1.97+1.22i.

Fig 1 Phase trajectory of real part

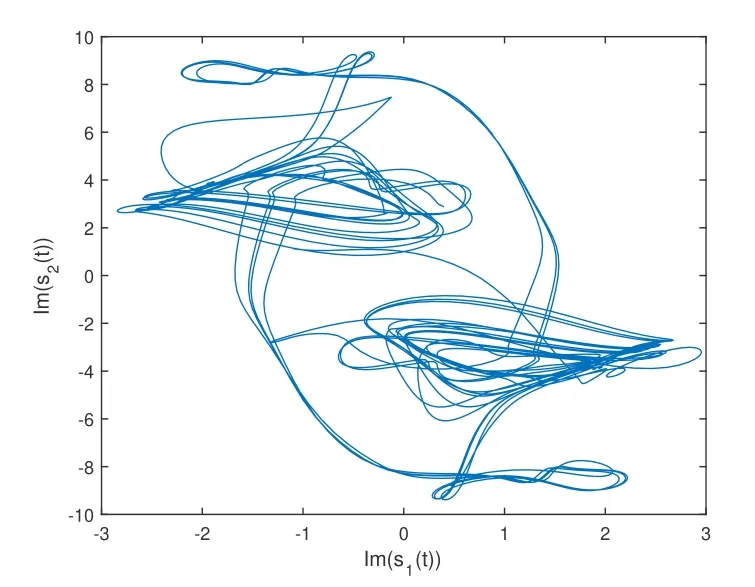
Fig 2 Phasetrajectory of imaginary part

For any 1≤i≤12,k=1,2,choose coupling function gk(xik(t))=tanh(Re(xik(t)))+i tanh(Im(xik(t))).By simple computation,Lk=νk=1,and Hk=2.In control scheme(8),select control parameters mi=14.70,ρ1=11.20,ρ2=34.26,and θ=1.42.From Theorem 1,systems(1)and(4)are fixed-time synchronized,which is shown in Fig 3 and Fig 4 whenβ=0.5 andβ=0 respectively,and thesettling timecan begiven as T*0=22.00,T*2=21.82.

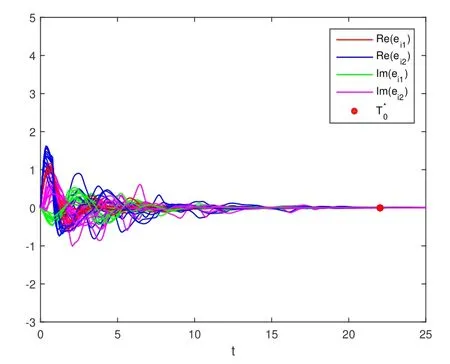
Fig 3 Synchronized error forβ=0.5

Fig 4 Synchronized error forβ=0

4 Conclusion

In this paper,the fixed-time synchronization has been discussed for a class of coupled MCNNs with time-varying delay.By introducing thecomplex-valued sign function and establishing anew fixed-timestability theorem,adiscontinuous complex-valued controller has been designed and a new Lyapunov function has been proposed in theoretical analysis.The proposed control scheme simplif ied the traditional design by excluding the linear part.Further work will focus on the fixedtimecontrol of impulsivesystemsand spatiotemporal models.