在争辩中揭示“真理”
顾文娟
[摘 要]教师始终是课堂的组织者、主宰者,一旦预设不充分,课堂很可能失控,但是预设过度过细,就会扼杀学生的创造力,束缚学生的思想活力。留出一个窗口,让学生一吐心声,教师趁机捕获他们创新思维的火花,趁机扇风助攻,就可以促成燎原之势。
[关键词]意外;面积;生成;争辩;沟通
[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068(2021)08-0032-02
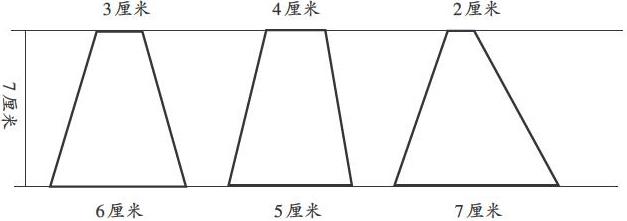
教学“梯形的面积”一课时,当学生推导出梯形的面积计算公式,并会套用公式进行基本的面积计算后,教师为了考查学生掌握的情况,出示了一道题:观察下图,根据这三个夹在一对平行线间的梯形提供的信息,你有什么发现?
一、意外的生成
通过计算、揣摩和讨论,学生发现,原来这三个梯形虽然上下底不是分别对应相等的,但是上下底之和是相等的,都是9厘米;高也相等,都是7厘米。因此,这三个梯形虽然形状各异,但是它们的面积一定相等。这时,笔者追问:“如果梯形的面积和高度都维持原值,它的上底和下底还可能出现哪些组合方案?”在学习“平行四边形的面积”和“三角形的面积”时,这类习题属于家常便饭,再加上前面学生之间的充分商谈,笔者深信学生完成这道题易如反掌。果然,大部分学生很快完成了任务。但是笔者发现还有一个小组仍在争论,一个平素口齿伶俐的男生面红耳赤。于是笔者走过去,和颜悦色地说:“说说看,你们在争辩什么?”该生委屈地说:“我认为只要梯形上底增加多少厘米,下底就随之减去相等长度,同时高保持不变,面积铁定不变,于是我开始动手操作,每次增减0.5厘米,一步步微调,没想到画到第三个图,梯形上下底都变成了4.5厘米,他们都嘲讽说我画错了。”
二、激烈的争辩
“错就错了,还抵赖,老师让画梯形,你卻画成平行四边形,驴唇不对马嘴。”同组的一个学生反驳道。
“老师要求的是保持面积和高度不变,没有硬性规定要画梯形呀?”男生说道。
其他学生也叽叽喳喳辩论起来。笔者欣喜于看到学生思想交锋的绚烂火花,智慧交流激荡起的波涛。所有人的兴奋点和情绪达到峰值,笔者决定抓住这一契机趁热打铁,把学生的思维引向深处,于是说道:“章平同学真厉害,他的思维方式很有逻辑性,条理清晰,思虑缜密,这样思考便于让潜藏的规律浮出水面!我修改一下问法,变为‘画出与已知梯形的面积和高分别相等的平面图形,按章平同学的思路去思考,能画出什么图形?”
学生边画边激动地在小组内交流意见,这就是无形中的交流合作。组际交流时,大家竞相发言:
生1:我们组画了好几个梯形,甚至还画出了原图的“孪生兄弟”,只不过上下颠倒。通过探究,我们认为与已知梯形面积和高分别相等的梯形有无数个。
生2:我们把上底和下底按照1厘米分档增减,上下底反向变化,最后居然画出了一个三角形。
生3:我们组画出了一个平行四边形。
生4:我们画出了一个倒置的三角形。
生5:我们画出了一个长方形。我认为,假如梯形上底与下底的和变为14厘米,画出正方形也不足为奇。
生6:我们发现一个重要规律,按照这种方式画下去,可以把所有的原图都来个“乾坤大挪移”——颠倒过来。
生7:我发现不同类型的图形不是独立存在的,而是有着千丝万缕的联系,它们之间可以相互转化。
师:既然这些平面图形之间关系这么密切,那么在计算它们的面积时,能否统一标准,归纳出一个通用的法则?
生8:可以统一归纳为梯形的面积计算公式。
生9:从动态角度考虑,把梯形的四个顶点当成动点,梯形上下底的线段长度视为联动的变量,和为定值9 厘米,那么当梯形的上底缩短至0厘米时,梯形就变成了三角形,其面积为(0+9)×7[÷]2=31.5(平方厘米)。
生10:当梯形的上下底等长时,梯形就变为平行四边形,其面积为(4.5+4.5)[÷]2×7=31.5(平方厘米)。
生11:还可以变成长方形或正方形,面积计算方法和平行四边形别无二致。
至此,教师一句点拨提醒的话也没有,甚至没有处心积虑地引导,学生在自发的“辩论赛”中将梯形的面积计算公式的推导原理、逻辑发展线索揭示得一览无余、一清二楚,教师在整个过程中做到了“无为而治”,起到的作用就是在课堂生成超出自己预设后没有慌乱,而是机智地表扬了章平同学,树立了一个创新的典型,引发学生纷纷仿效;当学生质疑时,没有一味维护章平同学,而是开明地让所有学生大胆提出异议,最后引导学生自主进行小组探究,并将各自的成果展示汇报,形成百花齐放的繁荣局面,真理在辩论中浮出水面。
三、捕获火花,大力褒扬
再来回顾上面的交流,多么精妙的答复,多么深邃的思想,多么了不起的发现!全程没有教师的过多干涉,教学基本是在学生你一言我一语的唇枪舌剑中推进的,这一切的获得是那么自然而然!我们在六年级毕业总动员时,曾绞尽脑汁、搜肠刮肚,也难在一节课的时间内将所有的平面图形全景式扫描地讲解,想要仅用一种方法沟通这些平面图形间的内在联系更是天方夜谭,至于用梯形的面积计算公式来推演、引申,转化出长方形、正方形、平行四边形、三角形等各种平面图形的面积计算公式,更是异想天开,但是这一切奢望在这一节课变为现实。
笔者激动地说道:“同学们真聪明!经过你们的分辩、探究、分工合作、考证、研讨、交流,沟通了各种平面图形的内在联系,开创出用梯形的面积计算公式推演出长方形、正方形、平行四边形、三角形等几何图形的面积计算公式这一别具一格、新颖独到的解题思路。这一独特的方法,谁是它的缔造者?”学生不约而同地将钦佩的目光都投向了章平同学,章平同学也显得自豪万分,脸上充满笑容。
实际课堂教学中,意外是不可避免的,防不胜防。面对令人猝不及防的课堂生成,教师要善于相机处理,随机应变,根据学生的新情况、新问题、新思维,打开新通道和新局面,不断主动调整自己的教学思路来适应学生的新需求,见机行事、因势利导,释放足够的空间和权利,让学生自由表达与表现,保护学生创新的火花不被浇灭,而不是一味执着于课前预设。相反,我们可以巧妙利用这些意外的课堂生成,将它们转变为助力课堂教学的踏脚石和登云梯,收到预料之外的精彩。
上述案例中,由于教师及时截获了这一积极的、有价值的意外生成,教学收获了意想不到的效果,学生不仅掌握了梯形的面积计算公式,还沟通了各类平面图形面积计算公式之间的隐藏关系,学生在争论中一步步逼近真相,揭开了梯形面积计算公式背后的秘密,品尝到了合作、探究、交流、解决问题的喜悦,思维能力得到锻炼。
(责编 吴美玲)

