解题教学,也要找准认知起点
王钰荥

[摘 要]通常认为,解题正确率越高,学生对解题技巧掌握得越深刻,但是,解题正确率不是评价教学效果的唯一指标,如果学生思辨能力得不到有效锻炼,就不足以应对各种变式,故此,找准学生认知起点,训练思维能力才是长久之计。
[关键词]比例;方程;单位;份数;解题;思维
[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068(2021)08-0024-02
偶然读到一篇数学教研论文,题为《最基本的,是最有效的》,全文对一道数学题的解答进行深度剖析,原题为:两条红丝巾的长度比为5∶4,各自剪短28 cm后,两条红丝巾余下的长度比为3∶2,两条红丝巾原长分别是几厘米?文中记述的解法为(5[x]-28)∶(4[x]-28)=3∶2,然后力证其有效性,并提供高达96%的正确率为佐证。笔者曾尝试如此教学,但效果极差,该解法的有效性不得不令人怀疑。
疑惑一:用方程解此类问题,毕业班学生能作出这么完美的解答吗?
疑惑二:如果换作笔者教学,该如何讲授?
【调查】
笔者曾对42位毕业班的数学教师进行视频访谈,设计了三大问题:
1.如此类方程:(4[x]-28)×3=(5[x]-28)×2,評讲起来是否有困阻?
A.有 B.没有
2.学生解方程的正确率应该落在哪个比例范围?
A.大于80% B.50%至80% C.小于50%
3.学生解方程的正确率可能超过95%吗?
A.有可能 B.不可能
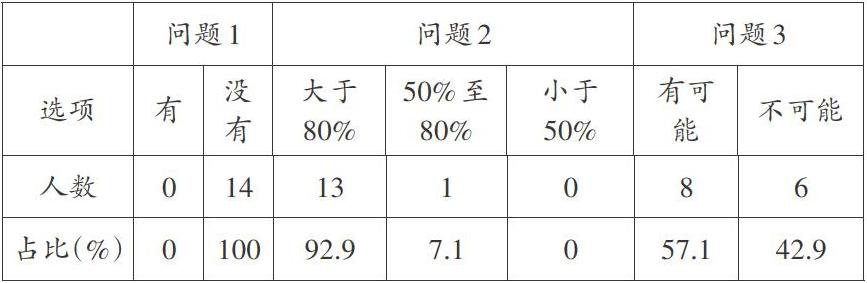
调查结果统计如下:
小学课本解方程部分内容以等式的基本性质为理论依据,适当插叙利用运算性质来解方程的方法。分析上表可知,对于等式两边都有未知数的方程,多数教师还是无法讲清它的解法,可想而知,学生的正确率高不到哪里去。同时,受访教师一致认为学生解方程的正确率高于95%是天方夜谭。
为了获取可靠情报,笔者在蹲点的学校七年级进行调查,这所区重点中学七年级共有25个班级,14名专职数学教师,对数学教师的调查结果统计如下:
初一的学生有“等式的性质”和“有理数的四则运算”等知识打底,受访教师普遍认为讲清这类方程解法不是难事,学生解答正确率直线上升,但是仍有部分教师对正确率达到95%信心不足。
综上所述,此类题若采用列方程解答,列方程容易,解起来却困难重重,就算教师示范解答,学生也只能机械模仿,无法心领神会,正确率自然要打折扣。这样的题型在课外教辅中屡见不鲜,如果换笔者进行教学,又该如何处理?学生解答这类题的认知起点在哪里?教师如何在追求正确率的同时,锻炼学生的思维呢?带着这些问题,笔者大胆进行专题教研。
一、揭示单位份数差异
片段一:教学基础题
[基础题1]班级庆祝端午节,买回10千克粽子,2千克发糕,5千克南瓜饼,粽子与发糕的质量比是( );粽子与南瓜饼的质量比是( )。
(学生口答)
师:同样是10千克粽子,为何在第一个比中占据5份,到第二个比中却变成2份呢?(将板书中的数字5和2标红)
生:第一个比中一份粽子的质量是2千克,第二个比中一份粽子的质量则是5千克。
师:同一数量,分成的最小的计量单位不同,包含的份数也不同。(板书:计量单位不同)
[设计意图:让学生从形象的物质配比中,深切认识到,同一数量,计量单位不同,包含的份数也不同,而这正是学生做后续拔高题的认知起点,如此教学为后续的学习打下根基。]
[基础题2]张志强与李水生的腰围比是5∶3,李水生与马爱国的腰围比是2∶3,你能判断张志强与马爱国谁的腰围谁更大吗?为什么?
生1:张志强的腰围大,因为张志强的腰围是5份,而马爱国的腰围是3份。
生2:反对,两个比的最小计量份数不一样,无法直接比较。
师:大家认为呢?现在无法比较,什么时候才能比较?
(生交流,认为应先将两个比中的最小计量份数统一标准)
师:如何将两个最小计量份数统一?
生3:李水生的腰围在前一个比中占据3份,到后一个比中变为2份,根据比的基本性质,将3份和2份统一切分化成6小份。
师:为什么偏偏选中6?
生4:因为6是2和3的最小公倍数。(板书:最小公倍数)
师:谁来详述转化过程?
(生说,师板书。张志强∶李水生=5∶③=10∶6,李水生∶马爱国=②∶3=6∶9)
师:原来两个比的最小计量份数有差别,可以借助比的基本性质,将李水生在两个比中占据的份数化成6份(在黑板上圈定6),如此一来,两个比的最小计量份数就统一了(板书:比例的基本性质,最小计量份数统一),就具有可比性。(此时,张志强和马爱国的腰围大小一目了然)
[设计意图:从对比腰围的生活情境中,让学生意识到单位份数不一样的两个比中的项无法直接比较大小,同时粗略领悟到借助比的基本性质,选择两个项的最小公倍数作为纽带,将最小计量份数统一。教师在黑板上圈定扩充后的项、演示“扩比”的操作步骤,教授学生必备技能。]
二、一个量不变下的解比例
片段二:教学拔高题“一个量不变”
[拔高题]甲乙两条红丝巾原长之比为7∶3,如果甲截短20米,两条红丝巾的现存长度比为3∶2,两条红丝巾的原长各有多少米?
师(启发):可否这样思考,甲原有7份,减去剩下的3份等于截短的4份,于是20米就对应着4份呢?
生1:不行,最小计量份数不同,不可以直接相减。
师:你怎么知道最小计量份数前后不一致?
生2:因为乙丝巾的长度自始至终没有发生改变,但是它的比值却由3份变为2份,有力证明了最小计量份数不相同。
师:能不能设法将前后的最小计量份数统一?请同学们演算一下。
(生独立作业,投影仪投影。课件出示:
原长构成的比例:甲∶乙=7∶③=14∶6
现长构成的比例:甲∶乙=3∶②=9∶6)
师:当乙占比6份的时候,甲的原长则随即调整为14份,现存长度则随即调整为9份。你能推定此时的最小计量份数是几吗?
(生尝试列式:20÷(14-9)=4(米))
师:你可以进一步求出两条红丝巾的原长吗?
(生尝试解答)
[尝试题]糕点房里粽子与发糕的质量比是5∶4,售出60千克粽子后,现有粽子与发糕的质量比是1∶2,糕点房里原有粽子多少千克?
(生独自尝试解题,然后集体评析)
(师课件出示解答过程:
原有粽子∶發糕=5∶④
现存粽子∶发糕=1∶②=2∶4
60÷(5-2)=20(千克);20×5=100(千克)
答:原来有粽子100千克)
师:比较上面两道题,你能找出解法的相同点吗?
最后,师生探讨并归纳“一个量不变”的比的问题的解法:先锁定前后两个比中恒定的数量;借助比的基本性质,将恒定的数量对应的最小计量份数统一;根据数值的变量和份额的变量的一一对应关系,算出最小计量份数的具体数量;利用份数对应的具体数量和份数求出结果。
[设计意图:在学生对例题的解法有了初步认知后,设计同类题,让学生进行模仿训练,将务虚的认知内化为实用的技能,现学现卖,学练结合,有利于增强学生的执行力。同时在对比中,归纳出解决类似问题的一般流程,编写解题程序,为后续的学习打下基础。]
三、正确率与教学效果的辩证统一
因为正确率达到了96%以上,就认为方法奏效,这是盲目乐观,须知“正确率高”与“方法有效”不能等量齐观。研究学生是否掌握解法,解题正确率充其量只能算一个末流的考量指标,解题时学生思维受训程度,能力提升层次等诸多因素同样重要。
教师进行解题教学务必要把准学生的认知原点,从原点出发,设计有难度梯级的题目,循序渐进环环相扣,这样才能锻炼学生的思维,锻炼学生的执行力,这样解题才能维持稳定的正确率而不是侥幸得手。当然,上述题型的解法并不唯一,比如用分数应用题中惯用的技法——假设恒等量为单位“1”,然后按照分数性质来解,也能行得通,但是这种解法学生的认知起点不一样,教师又需要重新定位。
原文作者尝试了“扩比法”后,由于效果欠佳,所以改弦易辙,换用方程法。殊不知,这样的方程属于七年级课程,超前教学无异于揠苗助长,没有训练学生的思维,即使学生勉力解出方程,提高的也是解方程的能力而不是解比的问题的能力。对于这样的题型,算术方法是重分析轻计算;方程法是重计算轻分析。
(责编 吴美玲)

