基于Timoshenko梁的盾构上跨对既有隧道纵向变形影响研究

韦征，江玉生

中国矿业大学(北京)力学与建筑工程学院，北京 100083

城市地下轨道交通因其高效、便捷等优势，在日常通勤中扮演重要角色。在城市轨道交通线网高密度化的趋势下，隧道间近距离交叉穿越的情况越来越多[1-7]。为保持既有隧道结构稳定性，在复杂的地质环境下，研究新隧道对邻近既有隧道的影响是十分必要的。

近年来，许多学者通过现场观测和理论分析[8-12]，研究了盾构上跨对既有隧道的影响；通过物理模型试验[13-16]定量研究盾构上跨过程中既有隧道与周围土体的关系；随着计算机软件的不断发展，人们通过数值模拟研究探讨复杂地质环境下的新旧隧道相互作用机理[17-23]。然而，这些研究大多没有详细研究盾构上跨过程中既有隧道的剪切变形及如何快速预测隧道变形的方法。

理论解析法以弹性力学为支撑，因其简单实用而被应用于快速预测隧道相互作用及内力计算。理论解的基本假设通常将隧道简化为等值长梁或弹性Euler-Bernoulli梁。Euler-Bernoulli梁理论假定，梁弯曲变形过程中其横截面始终保持不变并与弯曲轴线相垂直，如图1所示。然而，隧道是由错缝交叉的管片通过螺栓连接，连接处的剪切变形远大于管片自身的剪切变形，因此不能忽略螺栓连接处的剪切变形。

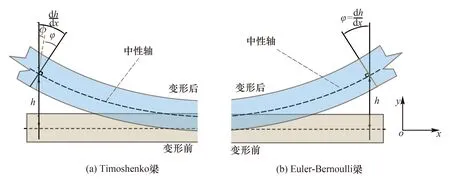
图1 Timoshenko梁与Euler-Bernoulli梁变形示意图Fig.1 Schematic diagram of timoshenko beam and Euler-Bernoulli beam deformation

隧道发生弯曲变形的同时，产生剪切变形，本文考虑了管片间接缝，对理论解析法进行改进。首先，将隧道简化为搁置于Winkler弹性地基上具有剪切变形的Timoshenko梁[24]，通过计算盾构开挖引起土体损失率对既有隧道位置处土体位移，建立隧道纵向位移平衡微分方程；通过有限差分法，求得纵向位移及弯矩、剪力、管片间错台量内力值。其次，通过盾构单线、双线上跨既有隧道工程案例，论证理论解析法的正确性。最后，通过与Euler-Bernoulli梁计算得到的弯矩、剪力等内力值对比，验证考虑隧道剪切变形的必要性。同时，分析土体损失率与既有隧道的纵向位移、弯矩、剪力及管片错台量的相关性。

1 隧道纵向位移理论解

1.1 盾构开挖引起地层位移

盾构上跨在既有隧道位置处引起的土体位移以纵向位移为主。本文采用Loganathan[25]在软黏土地层中由地层损失引起的纵向位移表达式。考虑盾构上跨既有隧道水平方向并非垂直穿越情况(图2)，对Loganathan给出的公式进行补充修正：

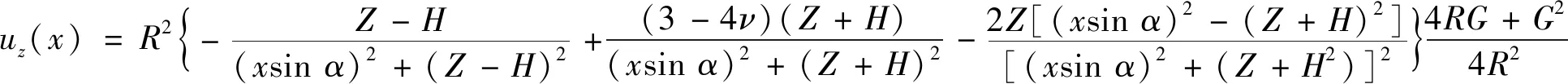
(1)

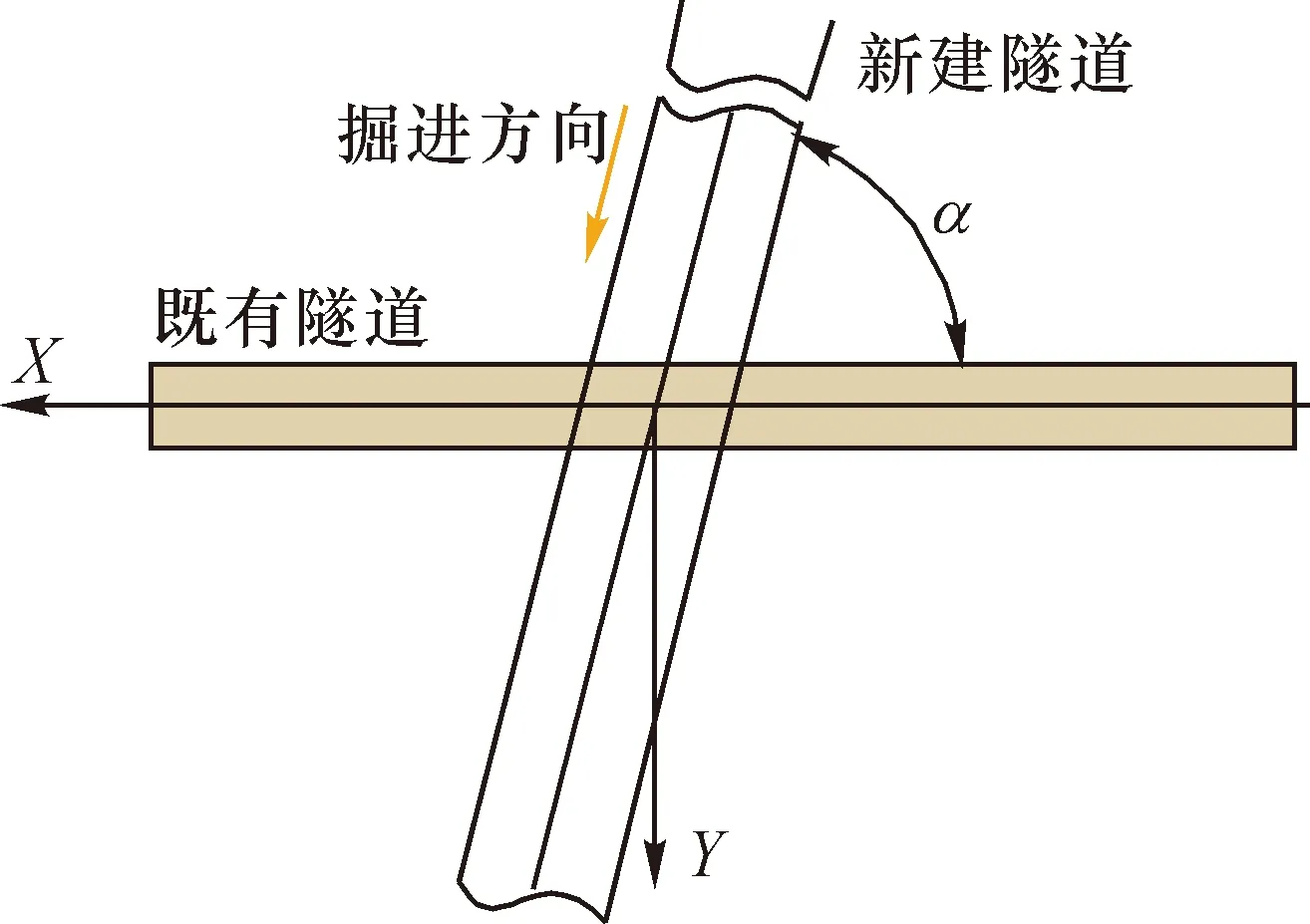
图2 盾构斜穿既有隧道示意图Fig.2 Schematic diagram of shield tunneling up-crossing existing tunnel at a certain angle

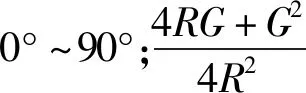
1.2 地层位移引起隧道纵向变形

既有隧道在盾构上跨引起地层位移作用下产生隆起变形及内力变化。考虑既有隧道接头对整体剪切刚度的削弱，采用Timoshenko梁模型模拟隧道的变形与内力变化。与Euler-Bernoulli梁理论不同，Timoshenko梁理论假定：在梁受力变形前，任意一梁截面与中性轴垂直相交；在受力变形后，梁截面不再与中性轴垂直相交，而且在剪切变形作用下截面与中性轴法线方向成一定夹角，并产生剪切变形，如图1所示；同时，隧道发生变形后，地层与隧道相互作用通过Winkler地基模型模拟，认为隧道与弹簧接触面不发生分离；土体简化为均质土层，暂不考虑土体固结沉降、蠕变。

图3为盾构开挖对既有隧道的纵向变形影响分析示意图。在地层损失引起的位移作用下，既有隧道剪力Q、弯矩M平衡方程如下：

(2)

(3)

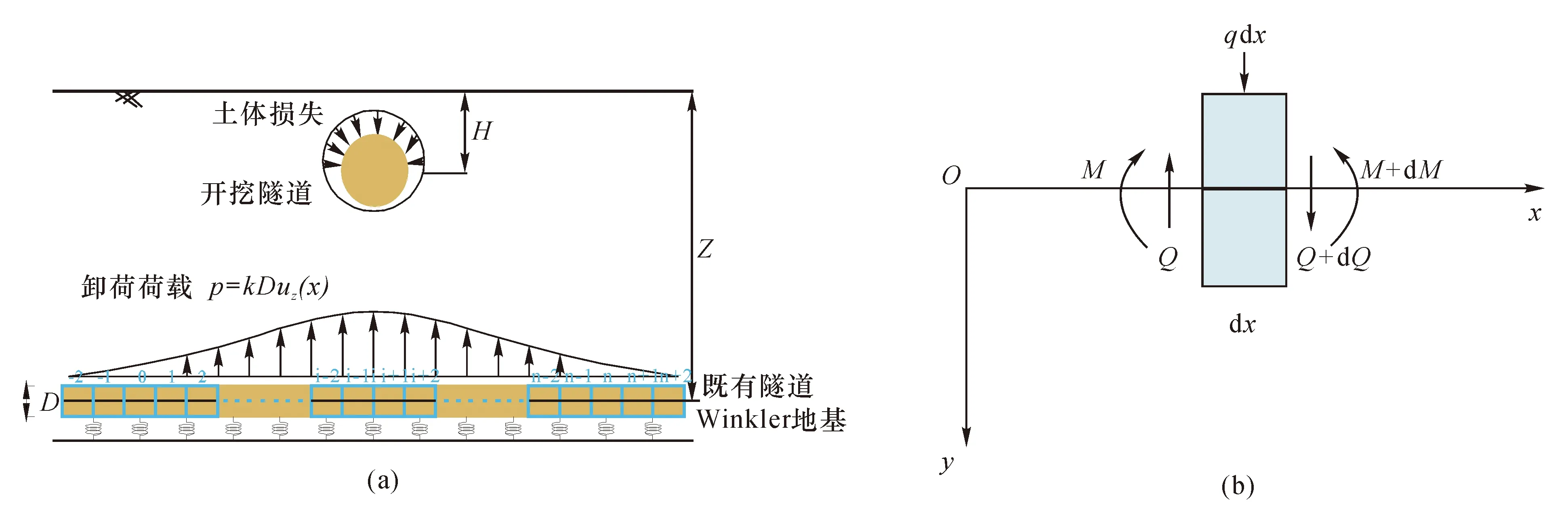
图3 盾构开挖对既有隧道的纵向变形影响示意图Fig.3 Schematic diagram of the influence of shield tunneling on longitudinal deformation of existing tunnels

式中，k为地基系数；D为隧道外径；h(x)为隧道纵向位移。

为了更加准确计算既有隧道的纵向变形与内力，考虑管片接头对隧道整体剪切刚度的影响，即隧道发生弯曲变形后隧道截面不再与中性轴垂直，隧道剪切刚度变化由图1几何关系计算得出。因此，将既有隧道简化为考虑剪切变形的Timoshenko梁，更能准确反映隧道弯曲变形大小及内力变化。

根据Timoshenko梁假定，隧道弯矩、剪力可表示为

(4)

(5)

式中，(EI)eq为隧道等效抗弯刚度；(κGA)eq为隧道等效剪切刚度。

联立式(1)至式(5)得到考虑隧道剪切变形的纵向位移平衡微分方程

(6)

式(6)为高阶常微分方程，不便于直接求解。基于有限差分原理，可将隧道等份额的进行差分。隧道被等份额差分为n+5个单元，其中4个虚拟单元位于隧道两端，每端各2个。单元长度为l。根据有限差分原理，式(6)的有限差分形式为

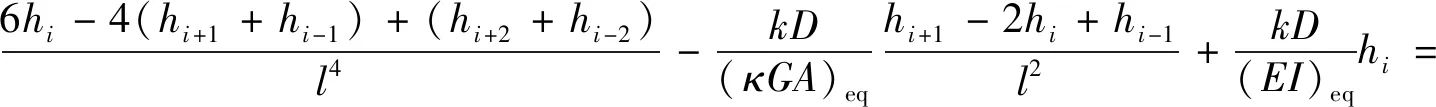
(7)

式中，hi-2，hi-1，hi，hi+1，hi+2分别为单元i-2，i-1，i，i+1，i+2纵向位移，uz，i-1，uz，i，uz，i+1分别为单元i-1，i，i+1通过修正后的Loganathan解得到的地层位移。

对于桩基边界，假定桩基两端自由，则桩基两端弯矩M及剪力分别为0，即

M0=Mn=0

(8-1)

Q0=Qn=0

(8-2)

根据有限差分原理：

(9-1)

(9-2)

(10-1)

(10-1)

由式(8)至式(10)得到，隧道两端额外4个虚拟节点单元的位移表达式如下：

(11)

令

式(11)代入位移方程式(6)，得

[K]{h}=[J]{U}

(12)

式中，{h}为隧道纵向位移矩阵；{U}为修正后的Loganathan地层位移矩阵；[K]、[J]分别为公式的系数矩阵。

(13)

{h}={h0(x)，h1(x)，h2(x)，…，hn-2(x)，hn-1(x)，hn(x)}T

(14)

(15)

{U}={uz，0(x)，uz，1(x)，uz，2(x)，…，uz，n-2(x)，uz，n-1(x)，uz，n(x)}T

(16)

式(12)转换成位移公式可表示为

{h}=[K]-1[J]{U}

(17)

式中，[K]-1为[K]的逆矩阵。

通过式(17)得到既有隧道纵向位移解析解。式(2)至式(5)得到隧道弯矩、剪力解析解。

当隧道等效剪切刚度(κGA)eq是无穷大，即不考虑隧道剪切变形时，上述方程将退化为基于Winkler地基的Euler-Bernoulli梁模型方程。

2 方程参数

考虑管片接缝对隧道整体剪切刚度的影响，一些学者将Timoshenko梁[29]应用于分析隧道的变形及内力。隧道发生弯曲变形横截面虽然为一平面，但不再与中性轴垂直相交，而是在剪切作用下截面与中性轴法线方向呈φ夹角(图1)，并产生剪切变形，根据力学平衡方程：

(18a)

(18b)

M=kcEIQ=φκGA

(18c)

式中，M为弯矩；Q为剪力；q为产生弯曲变形的外荷载；h为梁中性轴挠度；φ为剪切角；φ为横截面的旋转角；kc为中性轴曲率；E为土体弹性模量；I为梁横截面的面积惯性矩；κ为Timoshenko梁剪切系数；G为梁的剪切模量；A为梁的横截面积。

在以往的分析中，研究者通常将隧道假设为由连续的混凝土管片组成的筒体结构，如Euler-Bernoulli梁。这样仅能分析隧道的弯曲变形，没有考虑管片纵向与环向的螺栓接缝的存在，忽略了剪切变形。实际中，隧道产生弯曲变形的同时，伴随有剪切变形。因此，隧道简化成具有抗弯刚度和抗剪强度的Timoshenko梁，以下就从这两方面展开探讨。图4为Timoshenko梁简化模型。

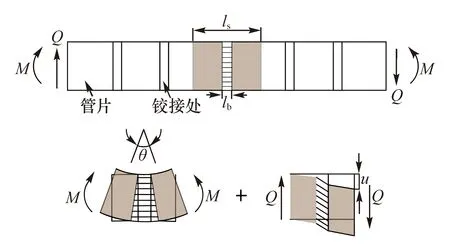
图4 Timoshenko梁简化模型Fig.4 Simplified model of Timoshenko beam

2.1 等效抗弯刚度

Liao 等[26]提出，考虑管片间接缝的存在，当隧道发生弯曲变形时存在一个等效抗弯刚度(EI)eq，使得旋转角θ等于管片转角θsg与管片间接缝转角θjt的和，即

θ=θsg+θjt

(19)

Shiba等[27]修正了等效抗弯刚度(EI)eq的计算方法(图5)，将两个半管片及管片之间螺栓接缝部分作为研究单元。管片部分的长度为lsg，螺栓接缝的影响长度为kljt，其中ljt为连接螺栓接缝的长度，k为螺栓接缝的影响因素。假定隧道发生弯曲变形时，隧道横截面保持平面，各横截面的中性轴位置相同；螺栓沿环向均匀分布，且具有相同的力学性能；不考虑螺栓的预紧力；螺栓承受抗拉变形，管片承受抗压变形。基于以上假定，根据环向管片间接缝几何关系，给出中性轴转角ψ与管片间接缝转角θjt的表达式如下：

(20a)

(20b)

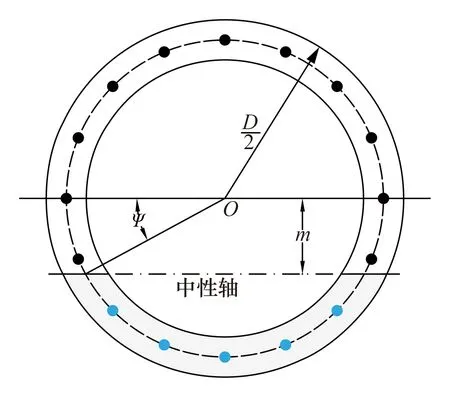
图5 等效抗弯刚度的计算图示Fig.5 Diagram of equivalent flexural rigidity calculation

式中，n′为环向螺栓个数；kjt为管片接缝处平动刚度；Esg为管片弹性模量；Isg为管片环截面的面积惯性矩；Ajt、Asg分别为螺栓和管片横截面积。

隧道发生弯曲变形时，管片间接缝的旋转角变化速率远大于管片旋转角。因此，假定管片旋转角变化在单位时间内被视为线性变化，即

(21)

将式(20b)、式(21)代入式(19)，得到隧道等效抗弯刚度表达式为

(22)

2.2 等效剪切刚度

Liao等[26]提出管片接缝影响范围的概念。当隧道发生剪切变形时，存在一个等效剪切刚度(κGA)eq，使得隧道剪切变形U等于管片剪切变形Usg与管片间接缝剪切变形Ujt的和，即

U=Usg+Ujt

(23)

(24)

(25)

式中，n′为环向螺栓个数；κjt、κsg分别为螺栓及管片环向剪切系数，对于圆形截面螺栓，通常κjt取0.9，κsg取0.5；Gjt、Gsg分别为螺栓剪切刚度及隧道管片剪切刚度；Esg、Ejt分别为管片、螺栓弹性模量；υsg、υjt分别为管片、螺栓的泊松比；Ajt、Asg分别为螺栓和管片横截面积。

将式(24)、式(25)代入式(23)，计算公式假设管片接缝处的剪力完全由螺栓承受，忽略管片间摩擦力。因此，引入等效剪切刚度修正因子μ对公式进行修正，本文取μ=1。同时，得到隧道等效剪切刚度表达式为

(26)

同理，根据几何关系，管片间接头缝隙处的错台量δ可表示为

(27)

2.3 地基模型参数

地基系数k是Winkler地基模型的重要参数。Vesic[28]通过等直长梁与均质各项同性地基相互作用的载荷试验，综合考虑梁的刚度与地层特性，给出地基系数表达式：

(28)

式中，Es为土体弹性模量；EI为梁的抗弯刚度，可用梁的等效抗弯刚度(EI)eq等值替换；B用隧道外径D等值替换。

Vesic提出的理论通过试验和工程案例得到了论证。然而，城市地下隧道具有一定埋深，此理论不再适用。Attewell等[29]考虑隧道埋深，修正了地基系数。本文采用Attewell等修正后的地基系数k表达式：

(29)

3 案例验证

3.1 单线上跨既有隧道

黄德中、戴仕敏等[30-31]报道了上海外滩隧道近距离以75°夹角上跨2号线双线平行隧道案例。如图6所示，2号线平行双线隧道外径同为6.2 m，内径5.5 m，环宽1 m，水平向距离14.4 m。轴线埋深27 m，位于灰色黏土和灰色粉质黏土间，地层土体物理参数见表1。因2号线所在地层有较高含水量，且抗压强度小，在上跨穿越过程中及通过后，对2号线隧道结构变形进行了实时监测。

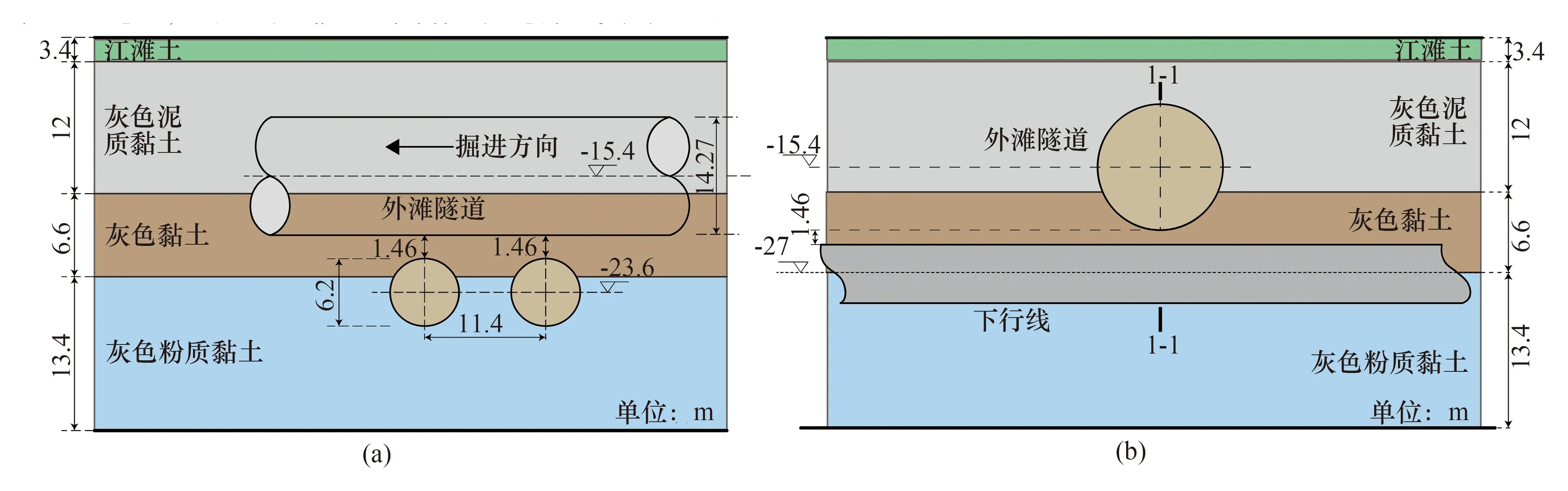
图6 外滩通道上跨2号线隧道示意图Fig.6 Schematic diagram of the Bund Passage up-crossing Line-2 tunnel

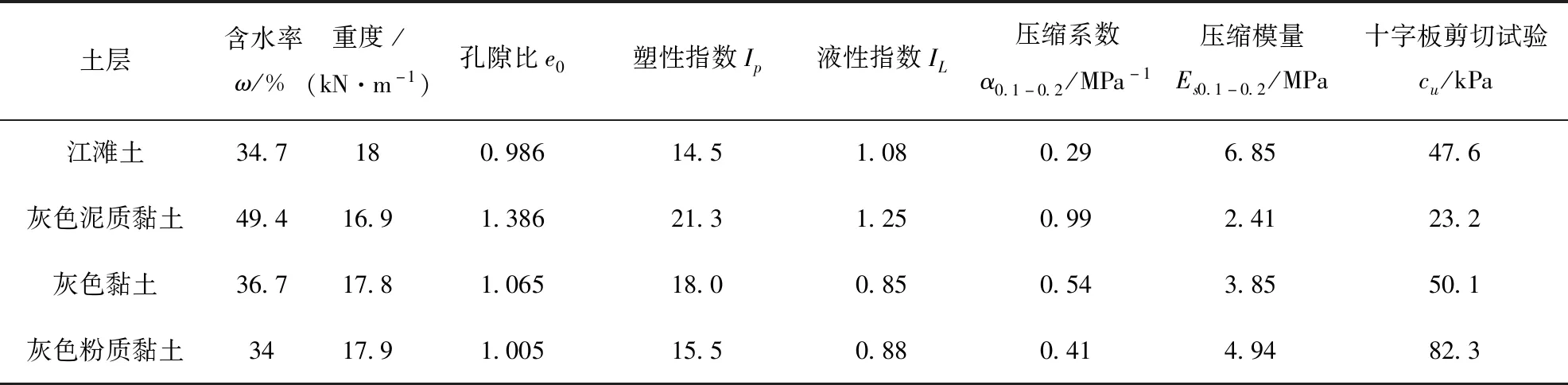
表1 现场地层力学参数Tab.1 Soil parameters of the site

新建上海外滩隧道采用土压平衡盾构法施工，主要穿越灰色泥质黏土层和灰色黏土层，如图6所示。开挖半径为7.135 m，隧道外径为13.95 m，隧道内径为12.75 m，衬砌管片厚度为0.6 m，环宽2 m，轴线埋深15.4 m。盾构掘进至既有隧道顶部，盾构底部距离2号线顶部最小间距仅为1.46 m。

2号线隧道衬砌结构力学性能参数见表2。根据式(22)、式(26)计算得到2号线所在地层等效抗弯刚度和等效剪切刚度分别为7.8× 104MN·m2，2.5×103MN/m。综合考虑既有隧道所在灰色黏土层和灰色粉质黏土层，土体泊松比取0.33，弹性模量取17.5 MPa。盾构上跨既有隧道过程中进行了良好的同步注浆，地层损失率取0.2%。

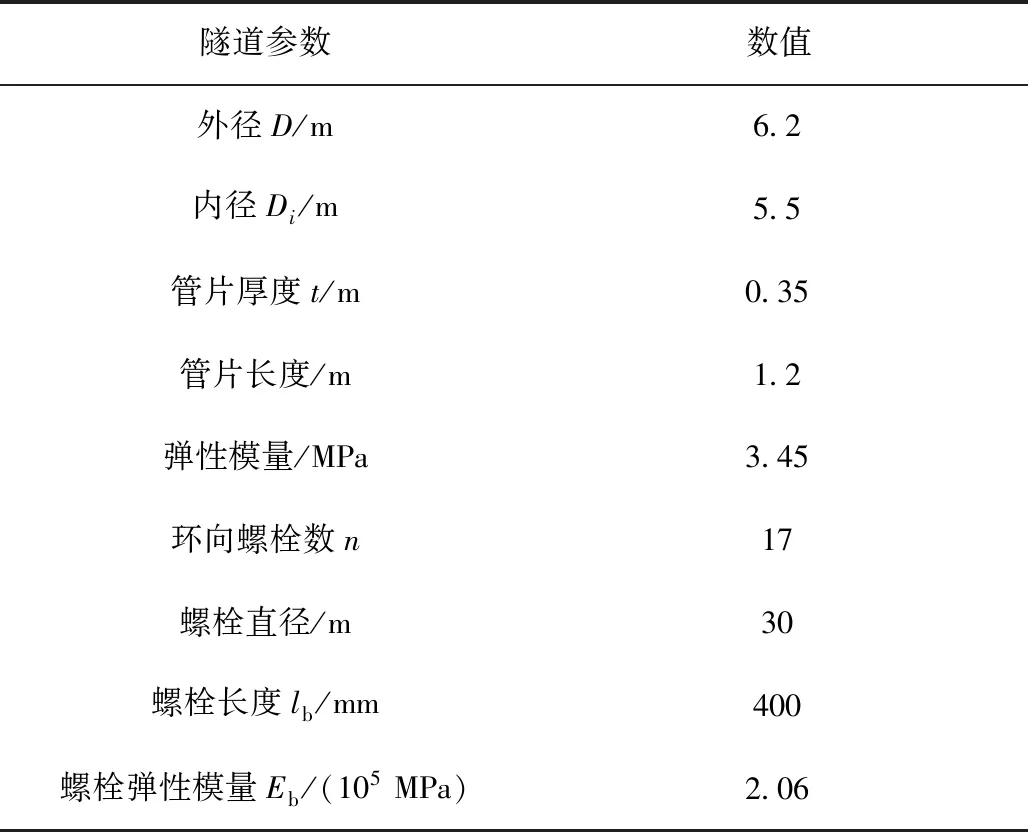
表2 2号线隧道管片参数Tab.2 Line-2 tunnel segment parameters

既有隧道在盾构穿越过后表现为隆起，2号线双线纵向位移理论值与实测值[31]趋势均保持一致，验证本文方法的正确性，如图7所示。

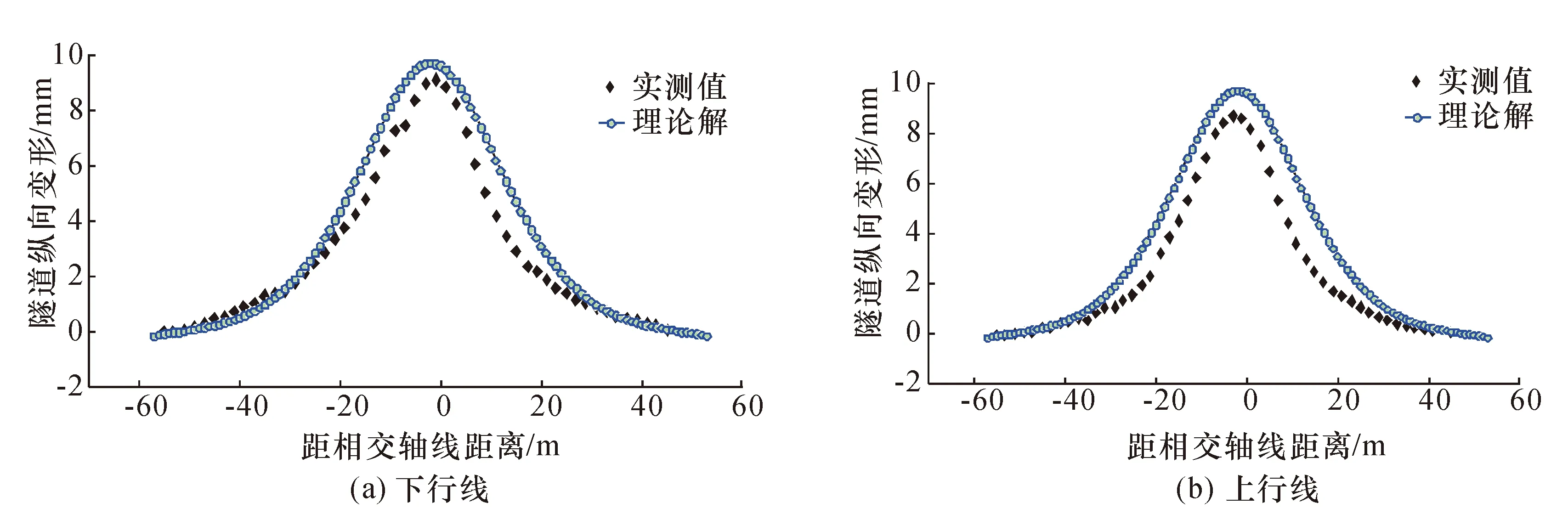
图7 实测数据与本文解析解对比Fig.7 Comparison between measured tunnel displacement and analytical solutions

3.2 双线上跨既有隧道

陈亮等[32]报道了上海地铁8号线上跨既有2号线工程案例。地铁8号线曲阜路站—人民广场站区间平行双线隧道，分别为上行线与下行线，采用土压平衡盾构法施工。盾构主要穿越泥质粉质黏土层、泥质黏土层和粉质黏土层。开挖半径为3.175 m，隧道外径为6.2 m，隧道内径为5.5 m，衬砌管片厚度为0.35 m，环宽1 m，轴线埋深15.4 m。盾构施工过程中上跨既有运营2号线风险源。

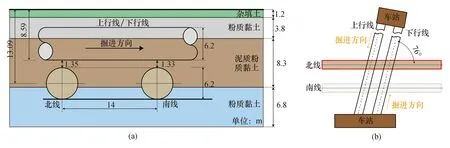
图8 上海地铁8号线上跨2号线示意图Fig.8 Schematic diagram of Shanghai Metro Line 8 up-crossing Line 2

既有2号线平行双隧道，外径与内径分别为6.2 m和5.5 m，环宽1 m，两隧道轴线水平向距离为18 m，其中南线、北线轴线埋深16.185 m和16.111 m。研究区间隧道所在地层主要为灰色黏土层和灰色粉质黏土层，主要土体物理参数见表3。

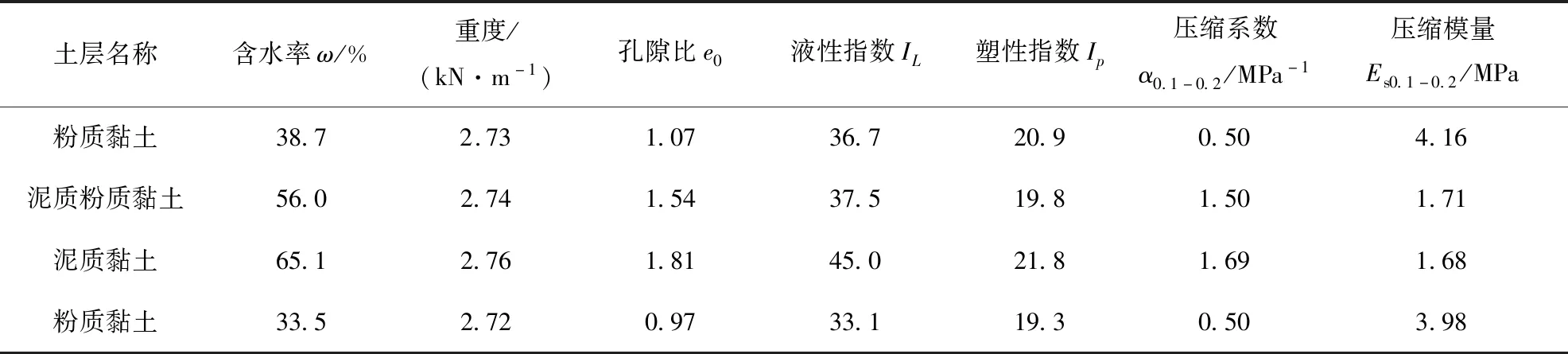
表3 现场地层力学参数Tab.3 Soil parameters of the site

盾构以水平方向76°夹角完成上跨穿越，盾构底部距离2号线南线、北线顶部最小纵向间距分别为1.33 m和1.35 m。为确保盾构施工对既有隧道稳定性，在上跨穿越前后对2号线纵向位移变形进行了布点监测。

根据表3地层参数，既有隧道所在土体弹性模量为17.5 MPa。取地基平均泊松比为0.33，由式(39)可得到地基反力系数k=3.76 MN/m3。根据吴昌胜等[33]计算方法，结合上海地区泥质粉质黏土层、泥质黏土和粉质黏土层盾构施工引起地层损失率计算公式，8号线盾构开挖引起的地层损失率为0.2%。根据式(22)、式(26)计算得到2号线所在地层等效抗弯刚度和等效剪切刚度分别为7.8×104MN·m2和2.5×103MN/m。

图9为隧道隆起理论解与现场监测结果对比图。8号线上行线第一次上跨2号线南线之后，2号线南线最大隆起值位于8号线上行线轴线处。计算值略大于实测值，与防止既有隧道变形过大采取抑制措施有关。8号线下行线二次穿越2号线南线之后，由于盾构二次上跨既有2号线南线引起纵向位移叠加，2号线南线最大隆起位置不在8号线下行线轴线处。对比计算结果与实测发现，计算结果虽然略大于实测值，但既有2号线南线隆起趋势与计算结果保持一致。此外，盾构二次穿越既有2号线北线隧道纵向位移具有同样的规律。

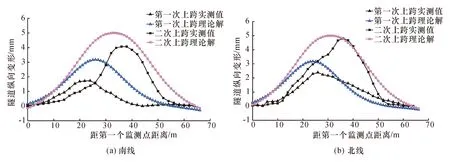
图9 2号线监测数据与本文解析解对比图Fig.9 Comparison between Line-2 measured tunnel displacement and analytical solutions

4 参数分析

通过与两个有代表性工程实例的比较，验证了所提方法的有效性。本节通过一系列参数分析，探讨了隧道剪切刚度、土体损失率等因素对既有隧道的影响。

4.1 剪切刚度影响

图10为考虑隧道剪切变形的Timoshenko梁与不考虑剪切变形的Euler-Bernoulli梁模型的隧道弯矩M、剪切力Q及管片错台量δ对比。

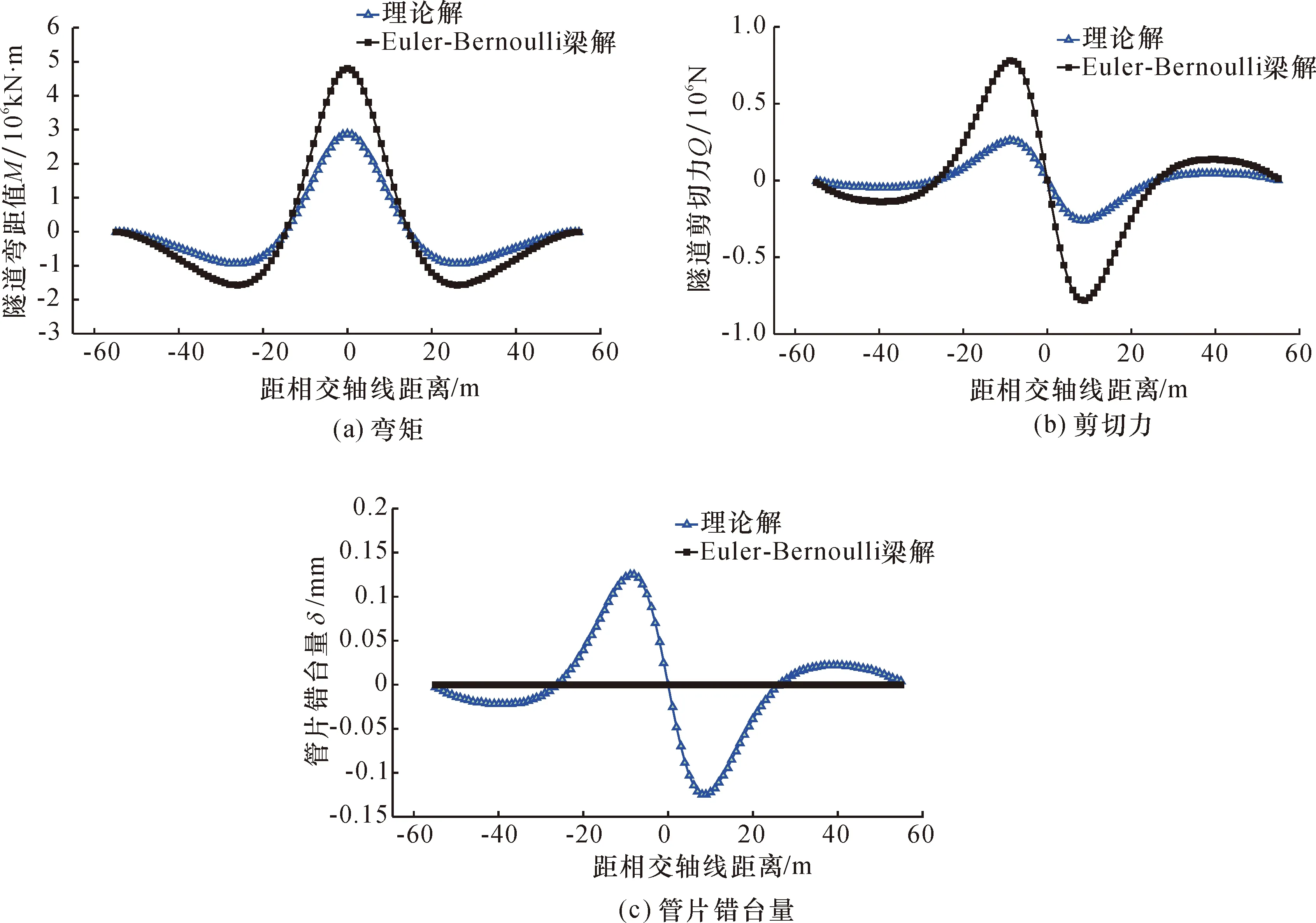
图10 Timoshenko梁与Euler-Bernoulli梁模型对隧道变形及内力影响的对比Fig.10 Calculation of tunnel longitudinal deformation and internal force by Timoshenko beam and Euler-Bernoulli beam

由图10对比发现，两者的隧道弯矩及剪切力变化趋势基本一致，但Euler-Bernoulli梁模型假定隧道等效剪切刚度为无穷大，不考虑剪切效应，计算得到的结果均明显大于Timoshenko梁模型计算值。Timoshenko梁考虑隧道剪切效应，可以进一步得到隧道的管片错台量δ变化。Euler-Bernoulli梁假定梁的等效剪切刚度无穷大，不能考虑隧道剪切效应，无法进一步得到管片错台量的变化。可见，基于Euler-Bernoulli梁理论的计算方法往往高估隧道的剪切力、弯矩等内力，若应用其结果进行隧道加固处理，势必导致加固过度保守，造成不必要的浪费。

随着隧道剪切刚度的增大，管片错台量逐渐减小(图11)，当隧道剪切刚度增大到一定值时，管片错台量变化趋于0。这是因为当隧道剪切刚度为无穷大时，Timoshenko梁模型退化成为不考虑剪切变形的Euler-Bernoulli梁模型。隧道只考虑发生弯曲变形、错台量为0时，不发生剪切变形。因此，在设计盾构隧道时，应保证隧道管片接头具有一定的抗剪强度，以免隧道管片错动较大造成结构破坏、漏水垮塌等问题。

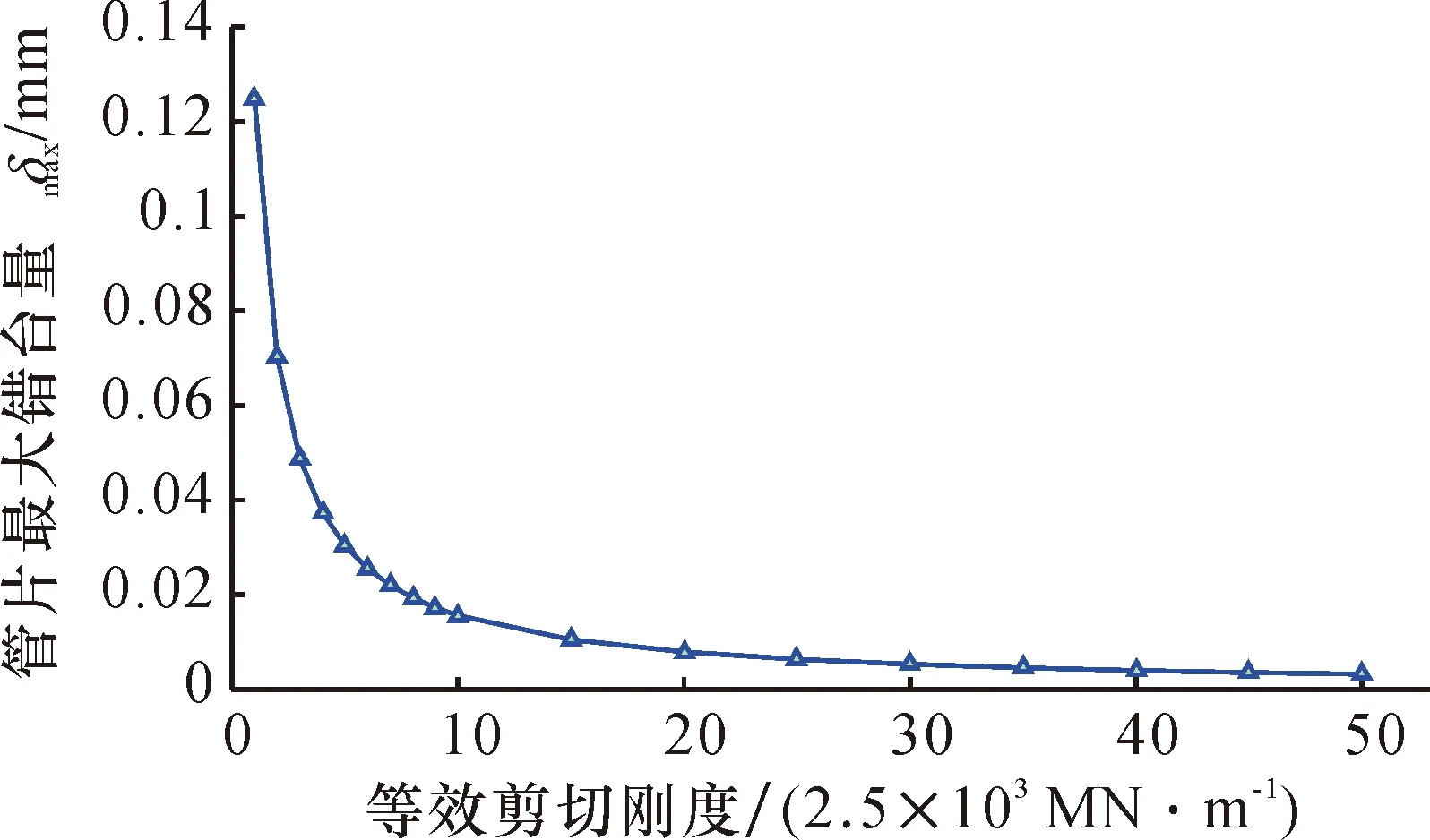
图11 等效剪切刚度对既有管片错台量的影响Fig.11 The effect of equivalent shear stiffness on the dislocation of segmen

5.2 土体损失率影响

图12给出了不同地层损失率V1与隧道最大位移Wmax、最大弯矩Mmax、最大剪力Qmax、管片错台量最大值δmax的对应变化关系，变化规律基本符合线性变化特征。一方面，土体损失率与隧道位移、弯矩、剪切力、管片错台量呈线性相关；另一方面，应加强对盾构施工的精确化操作，避免盾构脱离轨道而引起不必要的施工缝隙。当盾构施工过程中产生超挖时，应及时做好同步注浆填充，必要时进行二次补浆，降低土体损失率，从而减少隧道本身变形及内力。

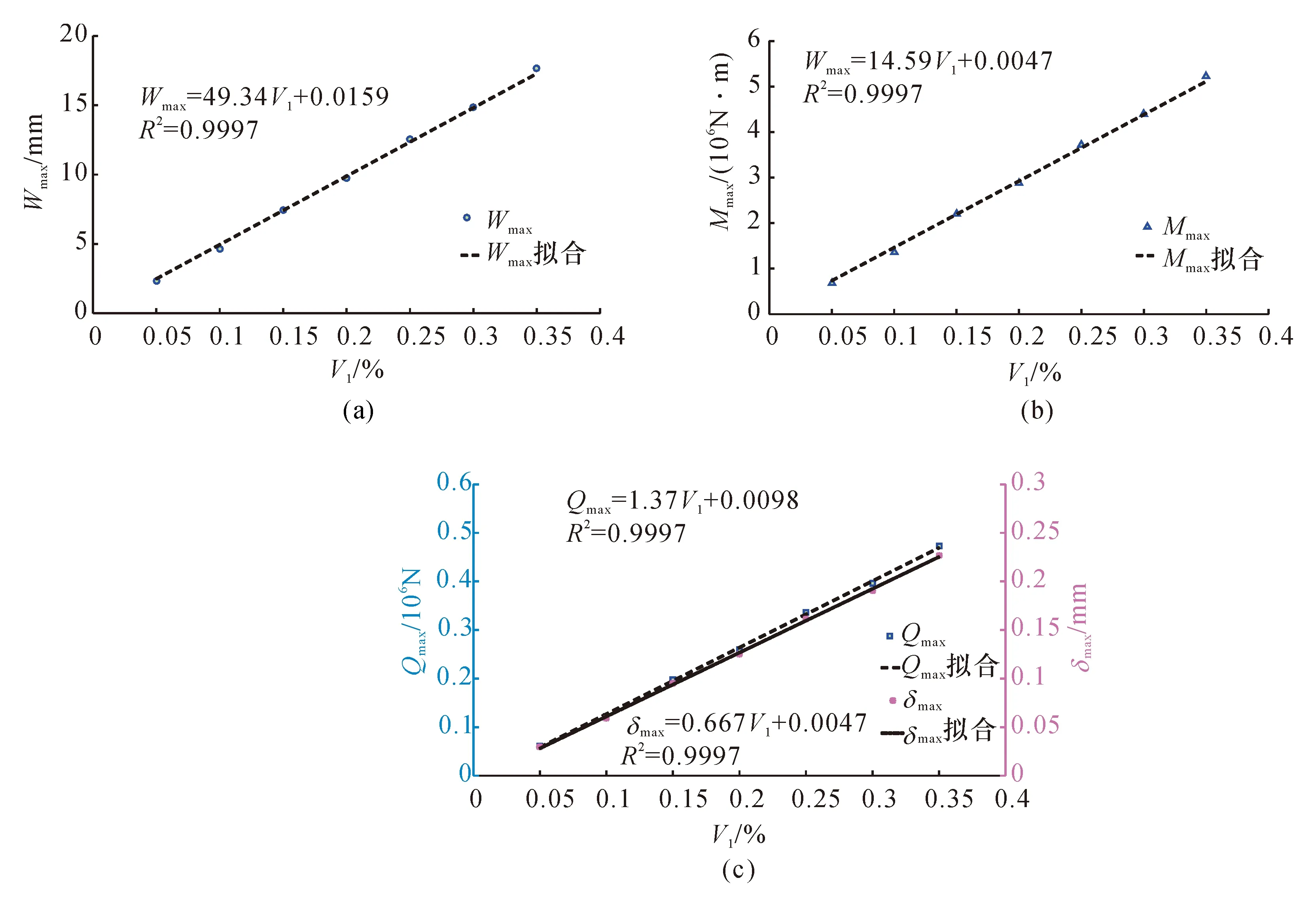
图12 地层损失率对隧道变形及内力影响Fig.12 Effects of ground volume loss ratio on dislocations and internal forces of tunnel

6 结 论

在理论解析法分析盾构上跨既有隧道时，常把隧道简化为弹性直梁或者Euler-Bernoulli梁，没有考虑隧道的剪切变形。本文提出了一种考虑隧道剪切变形的Timoshenko梁理论，用以研究盾构上跨对既有隧道变形及内力的影响。

修正的Loganathan理论计算既有隧道位置处的地层位移，建立基于Winkler弹性地基的Timoshenko梁关于纵向位移的微分平衡方程。采用有限差分法求解既有隧道变形及内力。Timoshenko梁理论不仅可以合理计算隧道弯矩、剪切力，而且能计算管片错台量，弥补了Euler-Bernoulli梁理论无法计算管片错台量的缺陷。通过案例分析，揭示了盾构开挖引起的土体损失率与隧道纵向位移、弯矩、剪切力、管片错台量变化呈线性正相关的规律。

本文理论模型没有考虑隧道所在地层不均匀特性和施工过程中支护、地下降水等因素的影响，在以后的研究中，可将这些影响因素考虑进去。