PBA法施工群洞开挖时空效应的理论计算模型

刘波，付春青，2，李东阳，杨航

1.中国矿业大学(北京)力学与建筑工程学院，北京 100083；2.北京住总集团有限责任公司轨道交通市政总承包部，北京 100027

PBA(Pile-Beam-Arch approach)工法为洞桩法的简称，是在传统浅埋暗挖大跨隧道分部开挖的基础上，综合盖挖法的特点发展而来的。采用PBA工法修建大跨隧道时，分步分块作业过程是关键。但是分块多会导致施工缝多，分步作业频繁会造成工序转换多，容易出现结构不均匀受力而带来的扣拱偏差，最终影响施工验收。例如，北京地铁15号线清华东路站采用PBA工法施工，由于施工难度大、受力转换复杂，存在施工周期长、作业空间狭窄的问题，造成车站结构纵向裂缝，导致防水效果较差等问题[1]。

PBA工法虽然对控制大断面暗挖地铁车站沉降具有一定的优势，但在导洞设计、小导洞内岩石地层成桩、大断面扣拱、拱部防水等方面要结合水文地质和结构特点进行细化才能确保施工质量[2]。造成PBA法施工车站质量问题的主要原因是群洞作业期间导洞施工的先后顺序不合适，引起地层应力重分布不均，且在水平方向上反复调整使地下结构极易产生变形裂缝。如何减小PBA法施工引起的地层沉降，是国内外研究者关注的重点问题。近几年的研究表明：群洞开挖阶段是引起地层沉降的主要阶段。研究者采用数值模拟方法分析控制沉降变形的关键因素，认为沉降主要发生在导洞开挖和扣拱施工阶段，这两个阶段地表累计沉降量分别为总沉降量的55%和80%，是控制地表沉降的关键工序[3]。

采用PBA法修建北京地铁14号线将台站时，由盾构隧道施工、侧导洞施工和中导洞施工引起的地表沉降分别占总沉降的11.2%～14.1%、45.4%～48.1%和30.1%～32.5%[4-5]。对北京地铁多条线路PBA法施工的车站地表沉降数据归纳研究表明，导洞开挖阶段和扣拱阶段的地表沉降之和约占总地表沉降的90%[6]。导洞开挖阶段的沉降占总沉降的71%，是PBA工法中控制地层沉降的核心工序[7]。

近年来，采用数值模拟方法研究施工过程对地表沉降的影响较多[8]。例如，比较分析洞桩法和洞柱法对最终地表沉降的影响[9]；PBA工法在研究不同结构形式下不同拱部施工顺序对结构受力与中柱位移的影响，指出在中跨扣拱先行施工的情况下，两侧边拱必须同步跟进，以避免因不对称结构带来的拱脚推力对中柱的不利影响[10]。

因此，针对群洞开挖阶段地层变形问题，研究PBA工法群洞作业的时空效应，是探究PBA法施工中扣拱偏差成因的关键。随机介质理论是解决地层沉降的一种非常有效的方法，能够同时考虑时间上的累积效应和空间上的相互影响[11-13]。本文采用随机介质理论，研究PBA工法群洞作业的时空效应，以期为制定合理的工程应对措施提供科学依据。

1 理论模型的建立

1.1 基本约定

地层沉降的整体坐标系方向按照右手规则确定，如图1所示。积分区域上下限的确定按照该坐标系定正负号。其中：X方向位移值，负值表示地层向负方向运动，正值表示向正方向运动；Y方向位移值，负值表示地层向负方向运动，正值表示向正方向运动；Z方向位移值，负值表示地层隆起，正值表示地层沉降。x，y，z为地下某处开挖单元体的局部坐标系。

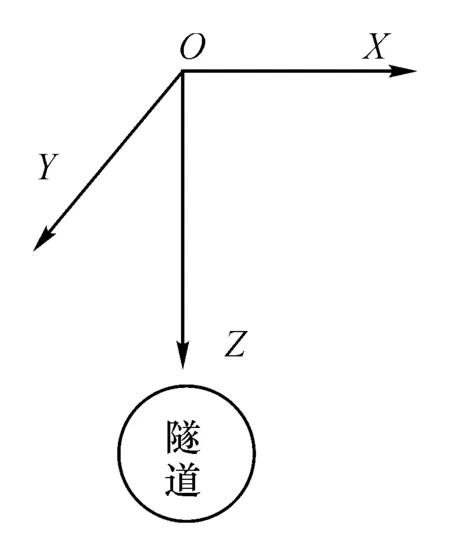
图1 随机介质理论模型计算的坐标系Fig.1 Coordinate system of stochastic medium model

假设开挖区域在Z的正方向，地层的影响角为β，如图2所示，则内部影响半径r(z)的计算方法为

(1)

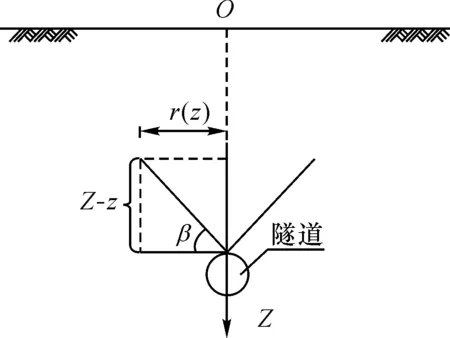
图2 内部影响半径示意图Fig.2 Schematic diagram of Internal influence radius

为方便书写，将tanβ(z)记为B。

1.2 竖向位移

对于各向同性均质体，根据随机介质理论[16]，在局部坐标系下，开挖一个微元体引起的竖向位移为

(2)

将式(1)代入式(2)，则由微元体dv=dxdydz引起点P(X，Y，Z)在整体坐标系的沉降值为

(3)

这是理论上一个无限小微元体引起的沉降值，式(3)只存在理论上的意义。对于整个开挖三维区域Ω，所有的微元体造成点P(X，Y，Z)竖向位移为

(4)

在直角坐标系中，则

(5)

式中，x1、x2、y1、y2、z1、z2分别为三维开挖区域Ω在x、y、z方向的积分上下限。

在考虑时间因素t的条件下，有

we(x，y，z，t)=(1-e-ct)we(x，y，z)

(6)

式中，c为地层沉降系数。

1.3 水平位移

同理，根据随机介质理论，开挖一个微元体引起的水平位移为

(7)

式(7)代入式(1)，则由微元体dv=dxdydz引起点P(X，Y，Z)在X方向的位移为

(8)

对应三维开挖区域Ω，所有的微元体造成点P(X，Y，Z)在X方向的位移为

(9)

在直角坐标系中，整理得到

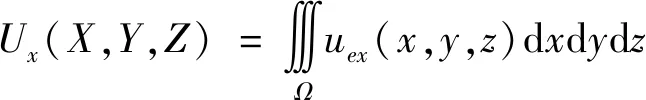
(10)

同理，对应三维开挖区域Ω，所有的微元体造成点P(X，Y，Z)在Y方向的位移为

(11)

1.4 多阶段沉降历时曲线的时间效应

PBA工法中的小导洞开挖是一个分步骤、多阶段的过程。通常包括：①小导洞开挖；②桩(柱)梁施工；③扣拱；④车站内部结构施工。为了在模型中体现时间效应和不同施工阶段地层沉降速度的差异，基于经典的随机介质理论[16]，假定对于某一方向，收缩边界的移动位移为s，则

(12)

其中，假设s0为最终边界的收缩量，则有

s=0，(t=0)
s=s0，(t=∞)

(13)

式中，c为地层沉降系数，可根据实测值或者经验值求得。则有

g(t)=g0(1-e-ct)

(14)

因地下工程中后一阶段的沉降是在前一阶段的基础上产生的，假设PBA工法施工的沉降过程分为4个阶段，则有

s1(t)=s01[1-exp(-c1t)]，t∈[0，t1]
s2(t)=s1+s02[1-exp(-c2(t-t1))]，t∈[t1，t2]
s3(t)=s2+s03[1-exp(-c3(t-t2))]，t∈[t2，t3]
s4(t)=s3+s04[1-exp(-c4(t-t3))]，t∈[t3，t4]

(15)

式中，s0i为第i阶段的最终沉降量；si为第i阶段的累积沉降量。

1.5 直墙圆拱断面掘进的边界变化

PBA工法导洞大多为直墙圆拱形，如图3所示。对于编号为Di的导洞，边界收缩后其地层损失由半圆形部分和矩形部分的损失组成。

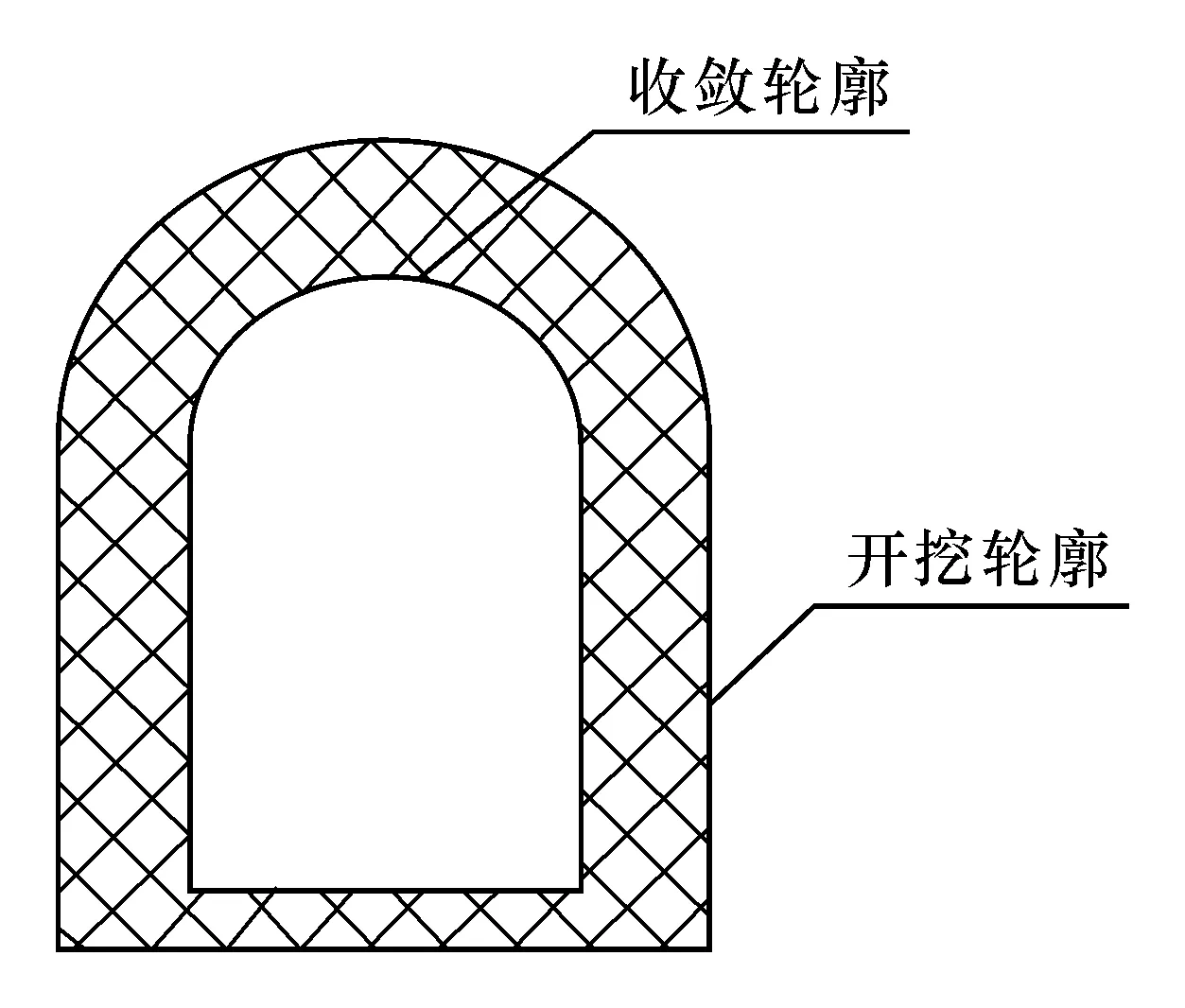
图3 直墙圆拱形断面收敛变形模式Fig.3 Convergence deformation mode of arch and vertical wall section

1.5.1 半圆形导洞部分

开挖后边界为

(16)

经过时间t因收缩而形成的新边界为

(17)

三维开挖区域的边界由ΩC1收缩为ΩC2后，所有的微元体造成点P(X，Y，Z)沉降值为

(18)

1.5.2 矩形导洞部分

对于矩形截面，开挖后边界为

(19)

经过时间t因收缩而形成的新边界，假设水平方向(x方向)的收缩量为s1，垂直方向(z方向)的收缩量为s2，则有

(20)

三维开挖区域形成边界ΩR1而后收缩为ΩR2，所有的微元体造成点P(X，Y，Z)沉降值为

(21)

直墙圆拱形隧道为半圆形和矩形的组合，编号为Di的导洞边界收缩后，所有的微元体造成点P(X，Y，Z)沉降值为

WDi(X，Y，Z，t)=WDi1(X，Y，Z，t)+WDi2(X，Y，Z，t)

(22)

地层的变形是由于诸多导洞施工进度不同造成的，则在t时刻N条导洞开挖引起点P(X，Y，Z)沉降值为

(23)

式(23)即为描述群洞开挖时空效应的计算模型，如图4所示。水平位移的计算模型与之类似，限于篇幅，这里不再赘述。

图4 导洞开挖计算模型Fig.4 Pilot tunneling excavation calculation model

1.6 数值计算流程

群洞开挖的计算流程如图5所示。其中对于三维三重积分采用高斯-勒让德法进行数值求解，采用MATLAB软件进行编程。

图5 群洞开挖时空效应模型计算流程Fig.5 The flowchart of calculating the space-time effect model for group hole excavation

2 计算实例

现场导洞是从两个施工横通道之间相向作业开始。开挖原则为：先下后上，先边后中，所以导洞施工顺序为导洞①④②③⑤⑧⑥⑦。首先进行下层边导洞①④的开挖，然后错距进行下层中导洞②③的开挖，接着错距进行上层边导洞⑤⑧的开挖，最后开挖上层中导洞⑥⑦。上层导洞与下层导洞、中间导洞与边导洞开挖掌子面均相互错开15 m。

2.1 第1步开挖

开挖下层边导洞①，导洞开挖一个单位步长如图6(a)所示，第1步开挖后的竖向位移云图如图6(b)所示。

地表沉降曲线的沉降槽在X=-11.60 m，地表沉降最大值0.82 mm，如图6(c)所示。地表水平位移在X=-11.60 m两侧向中心移动(正值表示向X轴正方向运动，负值表示向X轴负方向运动)，地表的水平运动位移值很小，最大值仅0.20 mm，且发生在地层内部。

根据计算结果，仅开挖一个导洞时，从俯视图上看，沉降槽的中心线是一条直线如图6(d)所示。

图6 第1步开挖位移Fig.6 The first stage of excavation displacement

2.2 第2步开挖

开挖下层边导洞④，边导洞①继续开挖，至导洞①开挖两个步长，导洞④开挖一个步长，第2步开挖后的计算结果如图7所示。

图7 第2步开挖位移Fig.7 The second stage of excavation displacement

开挖导洞④之后，地面沉降量开始增大，地表沉降最大值由0.82 mm增至1.60 mm。但是沉降的开始不对称，沉降槽的中心线开始向X轴正方向有轻微的移动。

2.3 第3步开挖

开挖下层中导洞②，导洞①④继续开挖，第3步开挖后的计算结果，如图8所示。

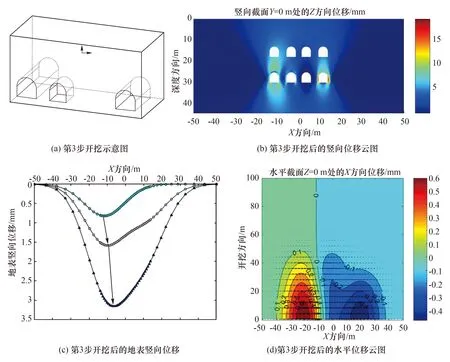
图8 第3步开挖位移Fig.8 The third stage of excavation displacement

导洞②开挖后，地面沉降量开始增大，地表沉降最大值由1.60 mm增至3.27 mm。

由于不对称开挖，沉降槽的不对称性开始加剧。沉降槽的中心线开始向X轴正方向移动，由第一步的-11.6 m至-6.5 m处，移动了约5.1 m。

2.4 第4步开挖

开挖下层中导洞③，已开挖导洞同速开挖，导洞①开挖4个步长，导洞④开挖3个步长，导洞②开挖2个步长，导洞③开挖1个步长，计算结果如图9所示。

图9 第4步开挖位移Fig.9 The fourth stage of excavation displacement

导洞③开挖后，地面沉降量继续增大，沉降最大值由3.27 mm增加至5.32 mm。沉降槽的中心线由第三步的-6.5 m处移动至-3.0 m处，向X轴方向移动了约3.5 m。

2.5 第5步开挖

开挖下层中导洞⑤，已开挖导洞同速开挖，导洞①开挖5个步长，导洞④开挖4个步长，导洞②开挖3个步长，导洞③开挖2个步长，导洞⑤开挖1个步长，计算结果如图10所示。

图10 第5步开挖位移Fig.10 The fifth stage of excavation displacement

导洞⑤开挖后，地面沉降量继续增大，最大值由5.32 mm增加至8.08 mm。沉降槽的中心线开始扭曲，在Y=0 m处，沉降槽中心线由第④步的 -3.0 m处移动至-5.5 m处，向X轴负方向移动了约2.5 m。而在Y=25 m处，沉降槽中心仍位于 -3.0 m处。整个沉降槽底部发生较大的扭曲变形。

2.6 第6步开挖

开挖下层中导洞⑧，已开挖导洞同速开挖，其中导洞①开挖6个步长，导洞④开挖5个步长，导洞②开挖4个步长，导洞③开挖3个步长，导洞⑤开挖2个步长，导洞⑧开挖1个步长。计算结果如图11所示。

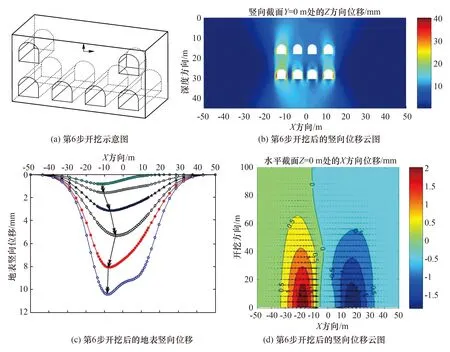
图11 第6步开挖位移Fig.11 The sixth stage of excavation displacement

开挖了导洞⑧之后，地面沉降量继续增大，最大值由8.08 mm增加至10.44 mm。沉降槽的中心线扭曲，在Y=0 m处，沉降槽中心线由第⑤步的-5.5 m处移动至-5.6 m处，向X轴负方向移动了约0.1 m。而在Y=36 m处，沉降槽中心位于-3.2 m处。整个沉降槽底部发生较大扭曲变形的位置，随开挖的推进再次发生较大变化。

2.7 第7步开挖

开挖上层中导洞⑥，已开挖导洞同速开挖，其中导洞①开挖7个步长，导洞④开挖6个步长，导洞②开挖5个步长，导洞③开挖4个步长，导洞⑤开挖3个步长，导洞⑧开挖2个步长，导洞⑥开挖1个步长。计算结果如图12所示。

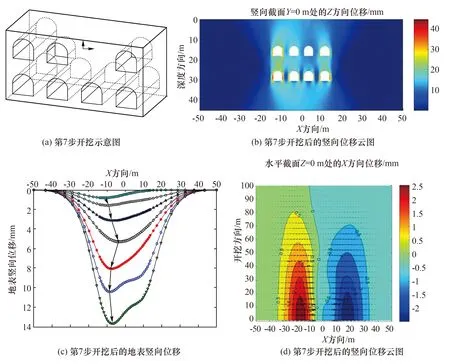
图12 第7步开挖位移Fig.12 The seventh stage of excavation displacement

导洞⑥开挖后，地面沉降量继续增大，最大值由10.44 mm增加至13.70 mm。

随着开挖的进行，沉降槽的中心线在开挖方向上继续扭曲，在Y=0 m处，沉降槽中心线由第⑥步的-5.6 m移动至-4.8 m处，向X轴正方向移动了约0.8 m。而在Y=52 m处，沉降槽中心位于-3.2 m处。整个沉降槽底部在后部趋于稳定，而前部开挖部分发生较大的扭曲变形。

2.8 第8步开挖

开挖下层中导洞⑦，已开挖导洞同速开挖。其中，导洞①开挖8个步长，导洞④开挖7个步长，导洞②开挖6个步长，导洞③开挖5个步长，导洞⑤开挖4个步长，导洞⑧开挖3个步长，导洞⑥开挖2个步长，导洞⑦开挖1个步长。计算结果如图13所示。

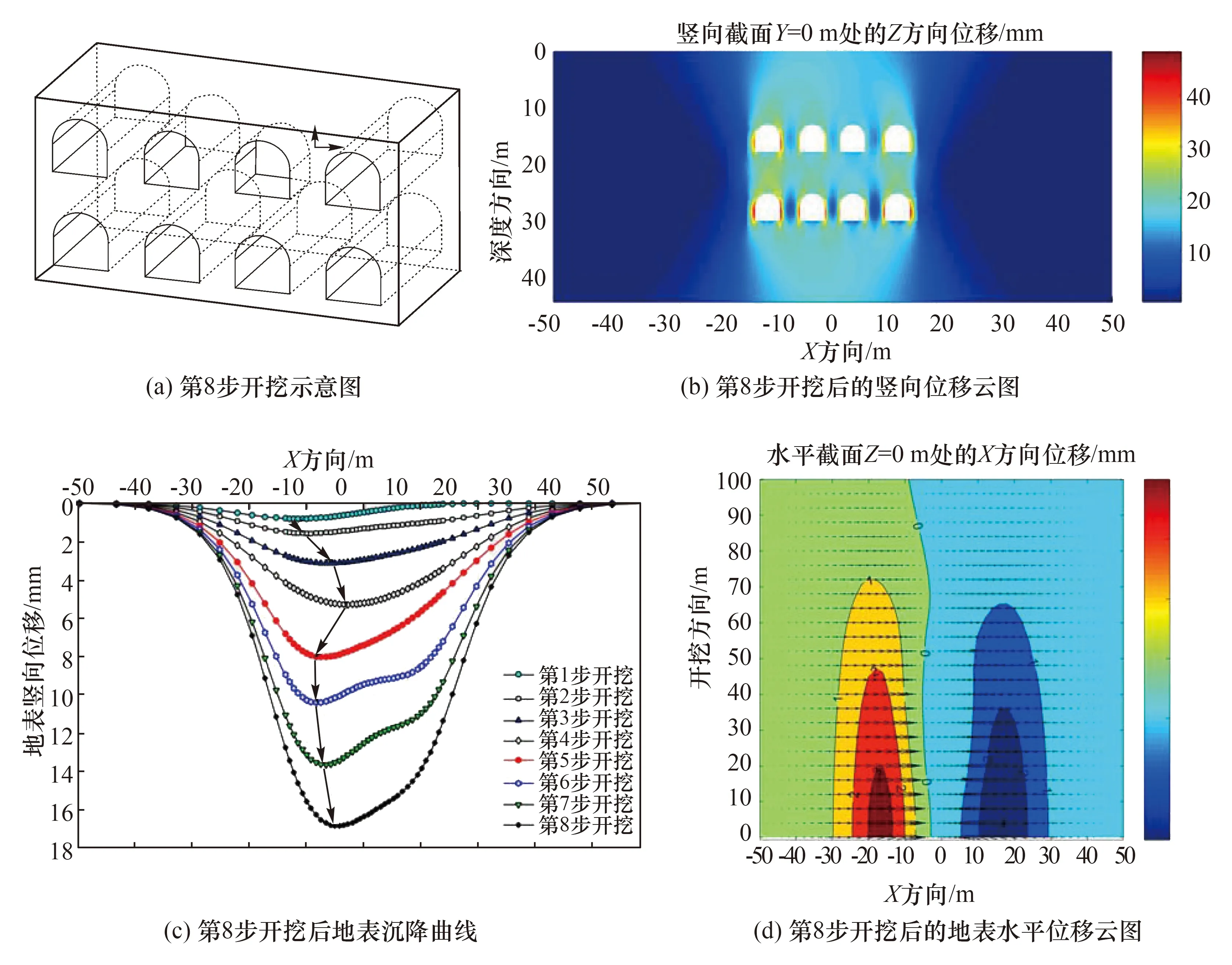
图13 第8步开挖位移Fig.13 The eighth stage of excavation displacement

开挖了导洞⑦之后，地面沉降量继续增大，最大值由13.70 mm增加至16.90 mm。最大沉降位置在车站中心处，即最大沉降值位置向右移动5 m。

开挖过程中，每步相对于上一个工序，最大沉降值逐步增加，完整体现了开挖过程中地层变化的时间效应。

3 扣拱偏差问题的分析与对策

车站大断面施工经常会出现扣拱偏差现象。根据第2节的计算分析，由于理想PBA工法左右对称同步开挖无法实现，群洞施工的非对称不同步，引起了隧道、地层和地面的复杂变化，不均匀受力、位移变形差异大，必然会引发多种工程质量问题。

特别是大断面隧道，分步作业时间较长、空间结构连接频繁，地层重复卸载-重分布-支护加载，隧道与地层之间不可避免地存在着空隙，隧道周边的围岩地层中连续发生复杂的力和位移变化。

虽然群洞效应不可避免，但是可以合理选择施工顺序。① 快速完成梁柱体系有利于快速形成竖向支撑，并对结构顶部地层形成有效支护反力。② 土体开挖按照先边跨后中跨的顺序，减小临空范围，缩短大跨临空时长。

大跨隧道断面分块施工顺序按照左右两侧分跨扣拱原则，竖向可分为三部分。如图14所示。

图14 大跨隧道断面分块施工顺序示意图Fig.14 Schematic diagram of the construction sequence for large-span tunnel sections

大跨PBA工法优化策略的总体思路就要考虑大跨合理逻辑分块、分跨顺序，合理有效管控施工空间临空范围、时空演化时长，从而减弱施工引起的隧道结构、周边围岩以及地表沉降变形趋势。

(1) 优化原则：大跨侧洞分跨、空间先边后中、跨内群洞对称、同步快速成环、侧洞先后成拱、中跨快速联拱。以此原则作为指导理念，在分跨作业中继续执行“先下后上、先边后中、同步对称”的作业工序。需要同步进行的工序是，小导洞在边跨内的群洞施工、柱梁体系的快速施工；不能同步对称的工序是，边跨拱部土体开挖支护、初支扣拱、断拱作业及二衬扣拱。需要错距组织的施工是左、右边跨整体施工以及部分小导洞开设马头门。跳仓作业是为了解决非同时大面积临空问题，可以调整工序，通过轻体台车的快速作业替代[14-15]。

(2) 工序调整：大跨在横断面内将8个导洞按车站中线分为左右两侧导洞(图15)，整个车站的施工组织按照左右分跨为单元进行。每个侧跨内4个导洞作为一个空间单元，群洞按照对称同步作业，快速形成2个柱梁结构体系。竖向支撑提前快速分跨扣拱，也是为侧跨成环提供时空条件，形成的侧洞分跨扣拱结构就是最先形成的柱梁拱(PBA)棚护结构。然后，在两侧开挖及初期支护依次进行，待侧洞二衬依次完成扣拱后，再进行中跨快速开挖、初支及二衬流水作业。

图15 PBA工法结构施工顺序Fig.15 Schematic diagram of structural construction sequence by PBA approach

因此，要从消除施工的左右对称无法同步入手，采取分别成拱封闭成环、快速作业的同洞同步作业和平行减小群洞作业影响的工程对策，通过侧洞分跨扣拱设计细化及施工优化来实现对称同步，以消除或减小扣拱偏差现象。

4 结 论

(1) 针对大垮PBA工法施工的地下工程出现的梁柱等结构尺寸偏差、初支裂缝和表观缺陷现象，分析了PBA工法左右不对称施工导致扣拱偏差的原因。

(2) 采用随机介质理论，建立群洞开挖时空效应的理论分析模型，对扣拱偏差现象产生的本质成因进行分析，分析了地表沉降槽空间形态随导洞开挖而左右摆动的变形规律。

(3) 指出了分别成拱封闭成环、快速作业的同洞同步作业和平行作业减小群洞影响，通过侧洞分跨扣拱设计细化及施工优化来实现对称同步是消除或减小扣拱偏差现象的主要对策。