有限群的可补子群的相关性质
周玉英
(哈尔滨商业大学 基础科学学院,哈尔滨 150028)
1 引言与预备知识
用G表示某个有限群,F*(G)表示群G的广义Fitting子群,F表示某个群系. 本文所用术语和符号可参见文献[1-4]. 设H≤G,如果存在K≤G,使得G=HK且H∩K=1,则称H是G的可补子群或称H在G中可补,并称K是H在G中的一个补群. 特殊子群的可补性质对有限群的结构有重要影响. 例如,G的任一Sylowp-子群均在G中可补当且仅当G中存在Hallp′-子群[1].
Hall[5]证明了如下经典定理:G是可解群当且仅当G的任一Sylow子群均在G中可补. 受Hall定理的启发,Arad[6]提出了如下猜想: 如果G的任一Sylow 2-子群及任一Sylow 3-子群均在G中可补,则G是可解群. Arad等[7]用有限单群分类定理证明了Arad猜想,进而将Hall定理推广为如下形式:G是可解群当且仅当G的任一Sylow 2-子群及任一Sylow 3-子群均在G中可补. Miao等[8]引入了M-可补子群的概念: 设H>1是G的子群,如果存在G的子群B,使得G=HB且对H的任一极大子群H1,都有H1B



引理4[16]设p,q是素数,a,b是自然数. 假设|G|=paqb,则G是可解群.
引理5[17]设G是非交换单群,p,q是|G|的两个不同素因子,a,b是正整数. 假设存在G的子群H1和H2,使得|G∶H1|=pa且|G∶H2|=qb,则G≅PSL(2,7).


2 主要结果
定理1设F是包含全体超可解群的群系,M>1是G的正规子群,且G/M∈F. 如果对M的任一极小子群H,H∩F*(GF)均在G中可补,则G∈F.

N=N∩G=N∩(HK)=H(N∩K).

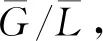
注1设F是包含全体交换群的群系,M是G的正规子群,且G/M∈F. 易见GF≤M∩G′. 因此,F*(GF)≤F*(M∩G′)≤F*(M)∩G′.
结合注1,可得如下推论:
推论1[13]设F是包含全体超可解群的群系,M是G的可解正规子群,且G/M∈F. 如果F(M∩G′)的任一极小子群均在G中弱可补,则G∈F.
推论2[14]设F是包含全体超可解群的饱和群系,M是G的正规子群,且G/M∈F. 如果F*(M)∩G′的任一极小子群均在G中弱可补,则G∈F.
定理2设M是G的正规子群,p是|M|的最小素因子,且P∈Sylp(M). 假设P的任一极小子群均在G中可补,则M在G中p-超循环嵌入. 特别地,M是p-幂零群.

H∩(M∩K)=H∩K=1,

定理3设M>1是G的正规子群,且M的任一极小子群均在G中可补,则M在G中超循环嵌入. 特别地,M是超可解群.

推论3假设G>1的任一极小子群均在G中可补,则G是超可解群.
推论4设M>1是G的正规子群,X是G的正规子群,且满足F*(M)≤X≤M. 假设X的任一极小子群均在G中可补,则M在G中超循环嵌入. 特别地,M是超可解群.
证明: 由定理3可知X在G中超循环嵌入,故F*(M)在G中超循环嵌入. 由引理7可知M在G中超循环嵌入. 特别地,M是超可解群. 证毕.
推论5设F是包含全体超可解群的饱和群系,M>1是G的正规子群且满足G/M∈F,X是G的正规子群且满足F*(M)≤X≤M. 假设X的任一极小子群均在G中可补,则G∈F.
证明: 由推论4可知M在G中超循环嵌入,由引理6可知G∈F. 证毕.
定理4如果G的任一奇数阶Sylow子群均在G中可补,则G是可解群.
证明: 先证明G的任一合成因子都是素数阶群. 用反证法. 假设存在G的合成因子K/L,使得K/L不是素数阶群,则K/L是非交换单群. 由引理4知|π(K/L)|≥3,由引理3易检验K/L满足该定理的全部条件,即K/L的任一奇数阶Sylow子群均在K/L中可补. 特别地,K/L满足引理5的全部条件. 由引理5知K/L≅PSL(2,7),但168阶单群PSL(2,7)中没有Hall 3′-子群(否则PSL(2,7)同构于A3的一个子群,矛盾),故K/L≅PSL(2,7)的任一Sylow 3-子群均不是可补子群,矛盾. 从而G的任一合成因子都是素数阶循环群,进而G是可解群. 证毕.
注2定理4的条件“G的任一奇数阶Sylow子群均在G中可补”不能削弱为“G的任一奇数阶Sylow子群均在G中弱可补”.
例1令G=PSL(2,7)×3,则|G|=23×32×7. 由于在PSL(2,7)中有24阶子群,从而G中有72阶子群,即G的任一Sylow 7-子群均在G中可补,从而在G中弱可补. 对任一R∈Syl3(G),注意到PSL(2,7) 定理5设|π(G)|=n,其中n≥3. 假设存在|G|的(n-1)个互不相同的素因子p1,p2,…,pn-1,使得对任一1≤i≤n-1,G的任一Sylowpi-子群均在G中可补. 如果G的任一合成因子均不同构于PSL(2,7),则G是可解群. 证明: 先证明G的任一合成因子都是素数阶群. 用反证法. 假设存在G的合成因子K/L,使得K/L不是素数阶群,则K/L是非交换单群. 由引理4知|π(K/L)|≥3,由引理3易见K/L满足该定理的全部条件,由引理5知K/L≅PSL(2,7),与G的任一合成因子均不同构于PSL(2,7)矛盾. 于是证明了G的任一合成因子都是素数阶群,从而G是可解群. 证毕. 注3注意到|PSL(2,7)|=23×3×7,并且PSL(2,7)的任一Sylow 2-子群及任一Sylow 7-子群均在PSL(2,7)中可补,但PSL(2,7)为非交换单群,进而是非可解群. 因此,定理5的条件“G的任一合成因子均不同构于PSL(2,7)”必不可少. 由定理5可得如下推论. 推论6[15]设|π(G)|=n,其中n≥3. 假设存在|G|的(n-1)个互不相同的素因子p1,p2,…,pn-1,使得对任一1≤i≤n-1,G的任一Sylowpi-子群均在G中可补. 如果G的任一截断均不同构于PSL(2,7),则G是可解群.

