基于深度残差网络的车标识别

田 强,贾小宁

(长春理工大学 理学院,长春 130022)

车标作为车辆品牌的独特标记,在智能运输系统车辆识别中具有辅助作用. 正确识别出车标已成为智能交通研究中的热门课题. Psyllos等[1]提出了一种基于增强型尺度不变特征变换(SIFT)的特征匹配方法,利用数据库特征的多种不同视图描述检测到的特征,使识别过程更准确；Llorca等[2]提出了一种基于梯度直方图和支持向量机的车标识别框架,并采用多数投票方法代替车标的精准定位；Yang等[3]提出了一种从粗到精的车标识别算法,首先对车标进行粗略定位,然后通过模糊检测等实现车标的精细定位,并最终输入支持向量机分类；耿庆田等[4]提出了利用SIFT进行特征提取,然后利用BP神经网络进行车标分类的方法; Xia等[5]将卷积神经网络和多任务学习相结合识别车标,应用自适应权重训练策略加速多任务模型的收敛,并达到了很高的车标识别准确率; Soon等[6]使用粒子群算法自动确定卷积神经网络的结构和超参数,不需要超参数的调整过程,因此减少了总训练时间,且该方法还降低了计算成本; 陈全等[7]提出了一种基于卷积神经网络(CNN)的车标识别算法,先对图像进行二值化等预处理,然后输入到卷积神经网络中进行训练和测试. 除车标识别外，神经网络在其他识别任务中也被广泛应用[8-11]. 本文提出一种改进的残差网络车标识别模型. 首先,使用改进的线性修正单元Leaky ReLU作为模型的激活函数；其次,调整传统的残差网络结构,并通过减少卷积核的数量加速模型训练. 实验结果表明,改进后的残差网络模型对车标的识别准确率较高.

1 预备知识

1.1 残差网络

残差网络[12]解决了普通卷积神经网络随着网络深度的增加而出现性能退化的问题,即随着网络深度的增加,普通卷积神经网络会出现训练不收敛的情况. 残差网络在普通卷积神经网络的基础上增加了恒等映射,当网络达到最优状态时,残差网络中的残差映射变为0,此时只剩下恒等映射,使网络一直处于最优状态. 根据网络深度的不同,残差网络模型可分为18层、34层、50层、101层和152层,本文参考18层的残差网络,并在其基础上进行改进. ResNet-18模型如图1所示.

图1 ResNet-18模型示意图Fig.1 Schematic diagram of ResNet-18 model

1.2 残差块

残差块由批量标准化、激活函数和卷积层组成,并且不同深度的残差网络中残差块略有不同. 由图1可见,ResNet-18模型的所有残差块均类似,图2为该模型的一个残差块.

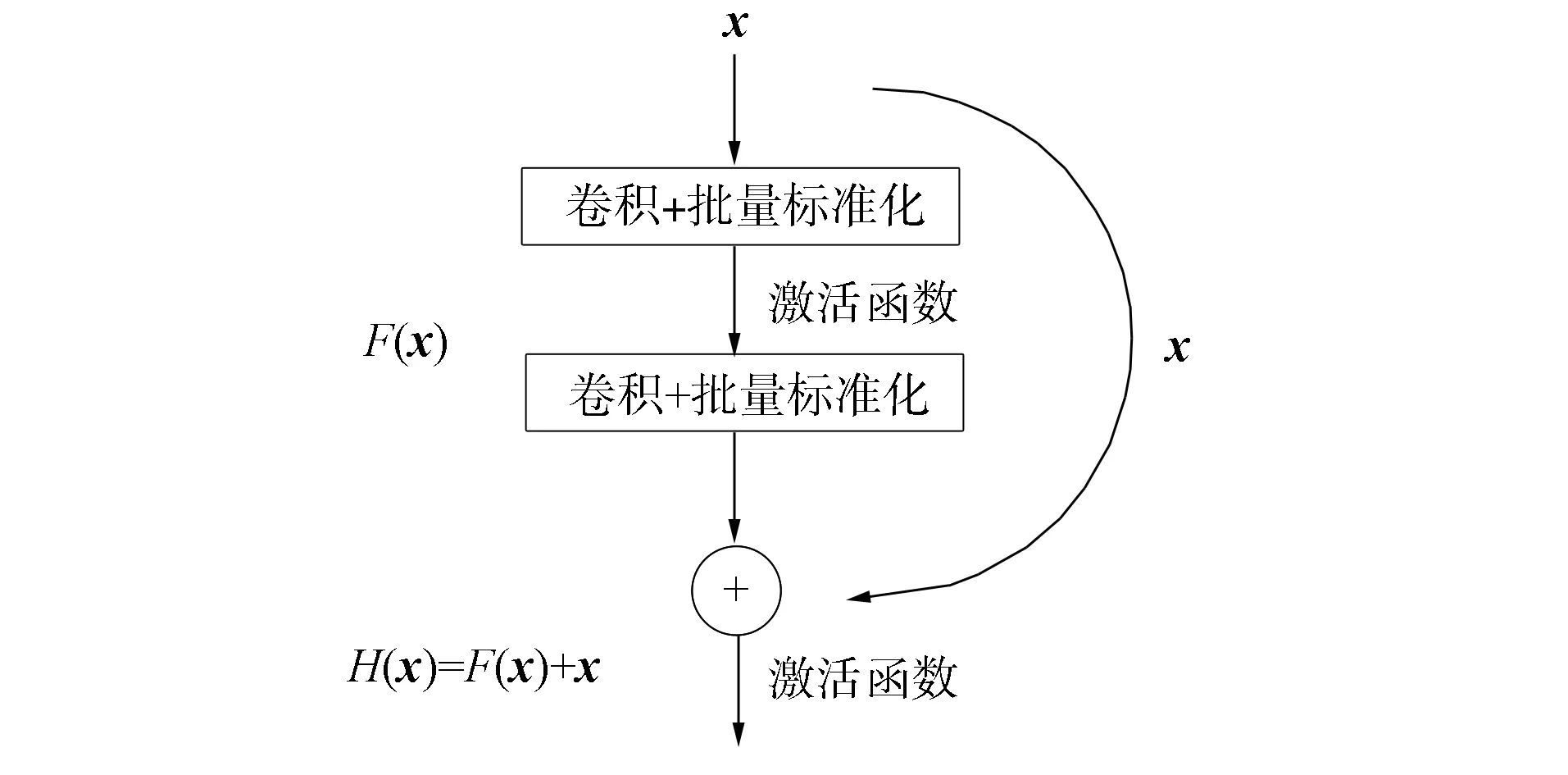
图2 残差块结构示意图Fig.2 Schematic diagram of residual block structure

残差块包含两种映射,一种是恒等映射(图2中曲线部分)；另一种是残差映射(除曲线外部分). 假设要求的最优解为H(x)=x,残差映射是指映射H(x)和x的差值,用F(x)表示,即F(x)=H(x)-x. 当F(x)无限接近于0时,网络达到最佳状态,继续加深网络深度,网络也将一直处于最优状态. 当残差块的输入为xn时,可得计算后的输出为

xn+1=f(xn+F(xn,Wn)),

(1)

其中F(·)为残差映射,Wn为相应的权重参数,f(·)为激活函数. 由图1可见,不同残差块之间可能存在维度不匹配的情况,此时只需对恒等映射xn做一个线性变换Ws即可：

xn+1=f(Wsxn+F(xn,Wn)),

(2)

其中Ws为权重参数.

2 基于残差网络的车标识别

2.1 改进的激活函数

传统残差网络用线性修正单元ReLU[13]作为激活函数. ReLU激活函数相对于S型激活函数有以下优点：1) 降低计算量；2) 解决梯度消失问题；3) 缓解过拟合. ReLU激活函数公式为

(3)

其中x为上一层的输出. 由式(3)可见,ReLU激活函数较简单,只需判别输入是否大于0即可. 当输入大于0时,保持不变；当输入小于0时,直接将梯度变为0. 即当输入小于0时,某些神经元的梯度变为0,并且有可能不再被任何数据激活,这些神经元将一直处于“死亡”状态. 此外,研究表明,当设置较大的学习率时,也会导致大量神经元“死亡”.

为解决ReLU激活函数存在的问题,本文使用Leaky ReLU函数作为网络的激活函数. Leaky ReLU激活函数公式为

(4)

其中x为上一层的输出,a为一个较小的常数. 由式(4)可见：当输入大于0时,Leaky ReLU激活函数和ReLU激活函数作用相同,使输入保持不变；当输入小于0时,由于已给定一个较小的常数a,Leaky ReLU激活函数可保证在输入小于0时信息不会丢失,梯度也可以正常传播,ReLU激活函数和Leaky ReLU激活函数图像如图3所示.

图3 ReLU激活函数和Leaky ReLU激活函数图像Fig.3 Graphs of ReLU activation function and Leaky ReLU activation function

2.2 网络结构的调整

传统残差网络首先经过卷积层,然后经过批量标准化,最后经过激活函数. 本文对网络结构进行调整,将批量标准化和激活函数放在卷积层前,使输入首先经过批量标准化,然后经过激活函数,最后经过卷积层,这样可以加强模型的正则化,减少过拟合的影响. 此外,通过减少卷积核的数量以减少网络中的冗余参数,从而加快网络训练速度. 实验结果表明,减少参数后的网络对识别准确率无影响. 图4为传统残差网络结构和改进后的残差网络结构示意图.

图4 残差网络结构示意图Fig.4 Schematic diagram of residual network structure

调整后的网络各层参数如下：

1) 输入层,图像尺寸为32×32；

2) 卷积层,卷积核尺寸为7×7,卷积核个数为64个,卷积步长为2；

3) 第一个残差块,卷积核尺寸为3×3,卷积核个数为64个,卷积步长为2；

4) 第二个残差块,卷积核尺寸为3×3,卷积核个数为64个,卷积步长为2；

5) 第三个残差块,卷积核尺寸为3×3,卷积核个数为128个,卷积步长为2；

6) 第四个残差块,卷积核尺寸为3×3,卷积核个数为256个,卷积步长为2；

7) Softmax层,分为10类.

3 实验结果

3.1 实验数据

实验所用数据均为人工收集,共收集1 968张图像,包含10类车标,如图5所示. 通过旋转加噪声等方式扩充数据集以满足实验要求,扩充后的数据集共含有训练图像15 452张,测试图像500张. 在训练前,对图像进行预处理,参考CIFAR-10数据集,裁剪训练和测试的图像尺寸为32×32. 本文的模型在操作系统为Windows10,CPU为Xeon(至强)E5-2620八核,32 GB内存上运行的TensorFlow环境中进行.

图5 部分车标Fig.5 Part of vehicle logo

3.2 实验结果及分析

从所有数据集中随机抽取50张图像作为测试集,并确保测试集不在训练集中. 图6为4种不同改进算法的训练损失. 由图6可见,在相同迭代次数下,改进的网络结构已达到了稳定,而未改进的网络结构还在收敛中,说明改进的网络结构速度更快,更具有实用意义. 图7为4种不同改进算法的识别准确率. 由图7可见,在相同迭代次数下,改进的网络更快达到了较高的识别准确率,而相对于只改进网络结构的算法,同时改进网络结构和Leaky ReLU激活函数的算法不仅快速达到了较高的识别准确率,并且更快地进入稳定状态.

对收集的车标数据集进行测试,测试结果分别列于表1和表2. 其中表1是本文算法在不同改进下的测试结果,表2为本文算法与文献[4]和文献[7]的测试结果. 由表1和表2可见,本文算法与3种不同改进算法和其他主流算法相比,识别准确率最高.

表1 4种不同改进算法的测试结果

表2 不同算法的测试结果

为验证本文算法的有效性,用本文算法对两种标准测试集CIFAR-10数据集和MNIST数据集进行测试,测试结果为：CIFAR-10数据集的测试准确率为90.0%；MNIST数据集的测试准确率为98.6%. 由测试结果可见,本文提出的模型不仅对人工收集的车标数据有较高的识别准确率,而且对标准数据集的识别也有较高的准确率,尤其是对MNIST数据集,准确率达98.6%,因此,本文算法具有很强的实用价值.

图6 4种不同改进算法的训练损失Fig.6 Training losses of four different improved algorithms

图7 4种不同改进算法的识别准确率Fig.7 Recognition accuracy of four different improved algorithms

综上所述,针对车标识别准确率的问题,本文基于传统的残差网络模型ResNet-18,提出了一种改进的残差网络车标识别模型. 首先,对激活函数进行改进,使用改进的线性修正单元Leaky ReLU作为模型的激活函数；其次,对网络结构进行调整,将批量标准化和激活函数放在卷积层前,并通过减少参数降低计算成本. 这两种方法的结合使得模型具有更强的识别能力. 实验结果表明,改进后的残差网络模型对车标的识别准确率达99.8%,表明本文算法具有很强的实用价值.