高速铁路场景中基于MAB模型的多信道选择算法

朱 豪,彭 艺,张 申,李启骞

(昆明理工大学 信息工程与自动化学院,昆明 650500)

在高速列车跨越小区时,为保证列车通信的连续性与高质量性,越区切换技术至关重要[1]. 本文主要研究在列车进行越区切换时,若切换区域是多基站覆盖的情形,列车应选择哪个基站进行接入通信,即在多信道存在的情形下,选择哪个信道进行接入可保证列车在具有高质量通信的同时又能有较长的接入时间,以保证乘客具有更好的通信体验.

目前,多臂老虎机(multi-armed bandit,MAB)模型被广泛应用于认知无线电的信道选择与接入领域. 文献[2]介绍了MAB模型及其实际应用,并对该模型进行了求解；文献[3]基于Q-learning讨论了双用户场景下双信道的选择接入问题；文献[4]讨论了基于bandit问题下的信道模型,提出了一种基于次用户与空闲信道利用的匹配算法,该算法虽可用对数函数的方式增长选择代价,但其需通过多个次用户之间进行信息的交互；文献[5-6]使用MAB模型进行分布式信道的随机选择与接入,其选择代价也是基于对数模式增长的; 文献[7]基于随机游戏竞价模型,对集中式信道的选择与接入问题进行了研究,通过竞价的方式能获得一定的频谱资源,但也会对资源分配有一定影响,进而影响回报值和选择策略；文献[8-9]提出了一种基于TDFS(time division fair share)的信道接入策略,通过将时间正交给认知用户分配信道,可使认知用户间在接入时间上达到公平；文献[10-11]建立了满意通信概率(satisfactory communication probability,SCP)模型,以解决列车高速移动过程中所产生的Doppler效应问题; 文献[12]讨论了在高速铁路环境下利用SCP使列车在越区切换过程中具有较低的平均切换次数,以保证较高的服务质量(QoS). 由于基站发射信号频率的不同,会产生多条不同频率的信道,因此,尽管相关文献都能在某种程度上实现信道的选择问题[13],但在高速铁路多变复杂的运行环境中,由于切换带的多基站分布而产生的多信道问题文献报道较少[14-15]. 基于此,本文提出一种基于MAB模型的多信道选择算法. 首先,以置信区间上界(upper-confidence bound,UCB)算法为基础,通过设置信道空闲差异因子,使算法能快速收敛于最优信道; 其次,由于列车移动过程中存在Doppler效应,因此引入SCP衡量移动列车的通信质量,并分析其与切换过程中误码率之间的关系；最后,利用一系列评判标准分析该算法的性能.

1 系统模型

1.1 场景介绍

图1为高速铁路场景下的多信道模型示意图. 当列车行驶至A点时,选择最优信道接入以触发越区切换. 在列车运行环境中,将列车视为一个认知用户,于是场景即等效为在一个CRN(city radio network)网络的高速铁路环境中,拥有n条信道,但只有一个认知用户的场景,其中n条信道之间互相独立,本文中假设其都服从Bernoulli分布,若信道处于忙碌状态,则不接入信道.

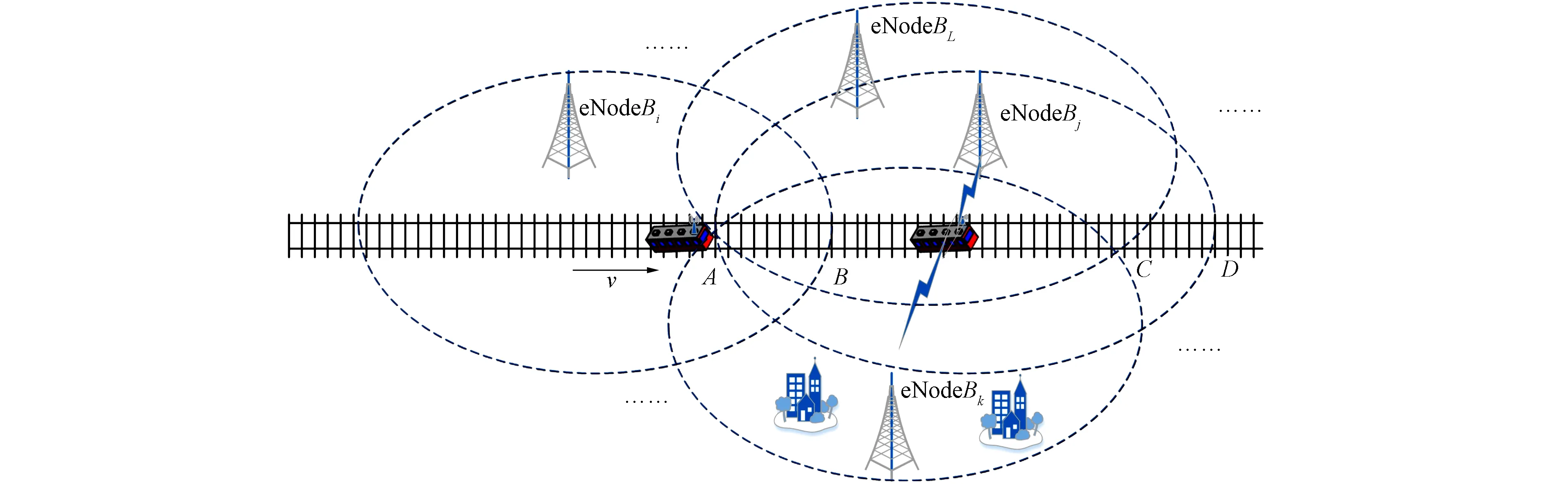
图1 多信道选择模型Fig.1 Multi-channel selection model

图2 信道模型Fig.2 Channel model

1.2 信道模型

在高速铁路场景中,切换带共被M个基站覆盖,表示M条信道,编号为N∈{N1,N2,…,NM},N(M)∈{0,1}. 当N(M)=0时,表示信道是空闲状态,空闲概率为Pi；当N(M)=1时,表示信道是忙碌状态. 信道模型如图2所示. 在每个时隙,认知用户伺机接入M个信道中的一个,且信道在每个时隙中状态保持不变. 认知用户在每个时隙的末尾,无论数据传输是否成功,都将进行数据更新. 定义fi(n)为到当前时隙为止,认知用户对信道M感知的次数；Ii(n)为感知总次数中信道空闲的次数. 则认知用户感知信道M的平均空闲概率可表示为

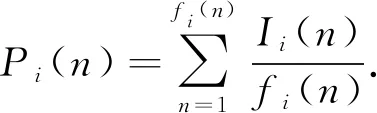
(1)

1.3 问题建模

在高速铁路环境中,由于列车的高速移动,在信号接收与发送过程中,将会产生Doppler频移,从而产生误码率. Doppler频移fD表示为

(2)

其中θ表示基站信号传输方向与列车移动方向的夹角,v表示列车的实际运行速度,c表示光速,f表示载波频率,dx和dt分别表示列车沿铁轨方向的水平距离和距离基站的垂直距离. 当列车沿铁轨方向不断前进时,由于dx变大,cosθ逐渐接近于1,故本文忽略距离对Doppler频移的影响,只考虑速度变化对其的影响,则Doppler频移可简化为

(3)

本文采用GMSK(Gaussian filtered minimum shift keying)调制技术,该调制模型下的误码率可表示为

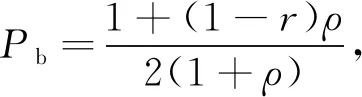
(4)

式中:ρ为信噪比,取值为15；r=J0(2πfDTb)为相关系数,J0为第一类零阶Bessel函数.

将高速铁路场景下列车越区切换过程中多信道选择与接入问题建模为MAB模型,即每条授权信道等效为一个独立的臂. 在高速列车运行环境中,经过n个时隙后,列车成功选择与接入信道的时间期望值T(n)可表示为

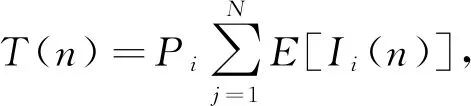
(5)

其中Pi表示信道空闲概率,Ii(n)为感知总次数中信道空闲的次数. 在MAB模型中,定义累积接入损失R(n)衡量MAB模型中算法的可靠性,表示为

(6)

其中n为时隙数,Pmax表示所有授权信道中空闲概率的最大值.

在MAB模型中,累积接入损失一定程度上决定了算法性能的优劣,R(n)越小,算法的性能越好,故在该模型中应尽量使累积接入损失最小. 由于nPmax的值保持不变,要使累积接入损失最小,则T(n)需最大,故该模型的目标函数变为

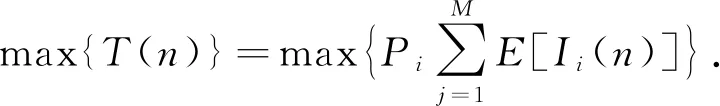
(7)

2 基于MAB模型的信道选择机制

2.1 算法设计

本文采用UCB算法进行高速铁路场景越区切换中单用户多信道的选择问题. 该算法是一种基于索引的算法,索引策略中索引的计算由当前信道的平均空闲概率和置信因子决定,使用户在探索当前可用信道的同时预测下一个空闲信道. 索引值计算公式为

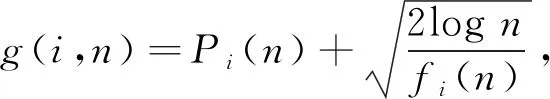
(8)

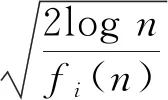
由于在信道探索过程中,无论信道空闲概率大小,都将对其进行探索,所以增加了算法的计算复杂度. 为使算法快速收敛于最优信道,故定义信道空闲差异因子βt反映信道质量的差异情况,表示为

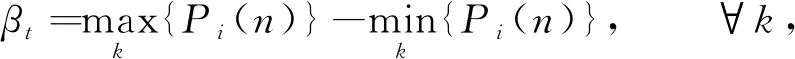
(9)

(10)

为反映列车移动过程中接收到来自基站之间信号质量的优劣程度,本文提出满意通信概率模型,进一步研究列车的选择与接入算法. 定义列车在运行过程中由于速度变化而产生的通信失败现象为速度-不满意通信事件. 由于该事件出现的方式是随机且独立分布的,且列车速度引起的Doppler频移是导致误码率的主要因素,故该事件在单位时间内的出现次数近似于服从Poisson分布,表示为

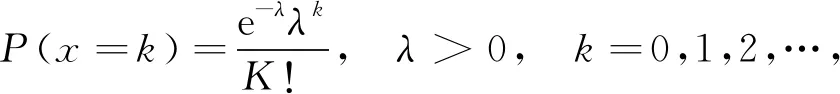
(11)

其中:K为出现误码的次数;λ为Poisson分布的均值和方差;λ=a(Pb-Pstd),a为待定系数,经过相关数据测试分析可知,a的取值一般为106. 定义通信失败次数小于临界速度-不满意通信事件次数的概率为速度-满意通信概率,可表示为

(12)

其中NPstd表示单位时间内发生误码的次数,由于误码是导致通信失败的最重要原因,所以NPstd也称为不满意通信事件的次数. 在GSM-R(global system for mobile communications-railway)要求中,通常Pstd的下限取为0.008. 本文算法流程如图3所示.

图3 基于UCB算法的信道选择流程Fig.3 Channel selection flowchart based on UCB algorithm

2.2 性能指标分析

本文将最优信道(空闲概率最大)选择比率作为算法的性能评价标准之一：

(13)

由于最优信道选择比率只能评价当前时刻选择的信道是否是最优信道,而无法评判所选信道在当前时刻是否是空闲信道,故此时需用成功传输率Psuc进行评判分析：

Psuc=T(n)/t,

(14)

其中T(n)为认知用户进行信道选择后接入的累积收益,即列车成功选择与接入信道的时间期望值.

根据式(13),用户总是选择最优信道进行接入通信,而非最优信道在未被占用时也可进行通信,故其累计接入损失在时间t足够长的情形下可调整为

其中Sm为逻辑表达式,信道被占用时取值为1,信道空闲时取值为0.

3 仿真结果与分析

3.1 仿真参数

仿真场景为：在高速铁路场景中,将列车定义为一个认知用户,假设多信道切换带中有9条待选信道,空闲概率分别为{0.1,0.2,…,0.9},各条信道服从Bernoulli分布,仿真总时隙为10 000,每个时隙的时长为0.01 s.

待选信道在有限时隙内被选择接入次数列于表1. 由表1可见,如果仿真时隙足够多,则信道空闲概率越大的信道被选择的次数越多,由于本文定义的最大信道空闲概率为0.9的信道9,故无论在原始UCB算法中还是在改进UCB算法中,信道9被选择接入的次数都最多,约占90%.

表1 待选信道在有限时隙内被选择接入次数

3.2 结果分析

图4 误码率与列车速度的关系Fig.4 Relationship between bit error rate and train speed

图4和图5分别为高速铁路场景下列车速度与误码率和满意通信概率间的变化关系. 由图4和图5可见,列车运行过程中的Doppler频移随着列车运行速度的不断提高而增大,从而导致误码率也越来越高,但总体上还是维持在一个较低水平1%～3%；同时导致列车高速移动时速度-满意通信概率降低,但当列车速度达到500 km/h时也基本维持在97%以上. 因此,在信噪比恒定时,列车运行速度越低,列车的满意通信概率越高,低速列车能更好地满足信道的有效接入.

图6为不同算法最优信道选择比率的对比结果. 由图6可见,由于随机选择算法选择的盲目性,在算法开始时就会直接选择第一条信道,故开始会出现选择比率达到1的情形,但随着时隙数的增加,选择比率急剧下降,其性能最差,最终约为11.7%；原始UCB算法的最优信道选择比率随着时隙数的增加而不断增大,在时隙数t达到约5 300时,选择比率可达80%,最终逐渐趋于稳定,维持在约86.5%[16]；而改进UCB算法,由于本文设置了信道质量差异因子,缩减了探索信道的数量,故在时隙t仅约为770时,便能很快达到90%以上的最优选择比率,并随着时隙数的增加而不断增长,最终逐渐趋于1.

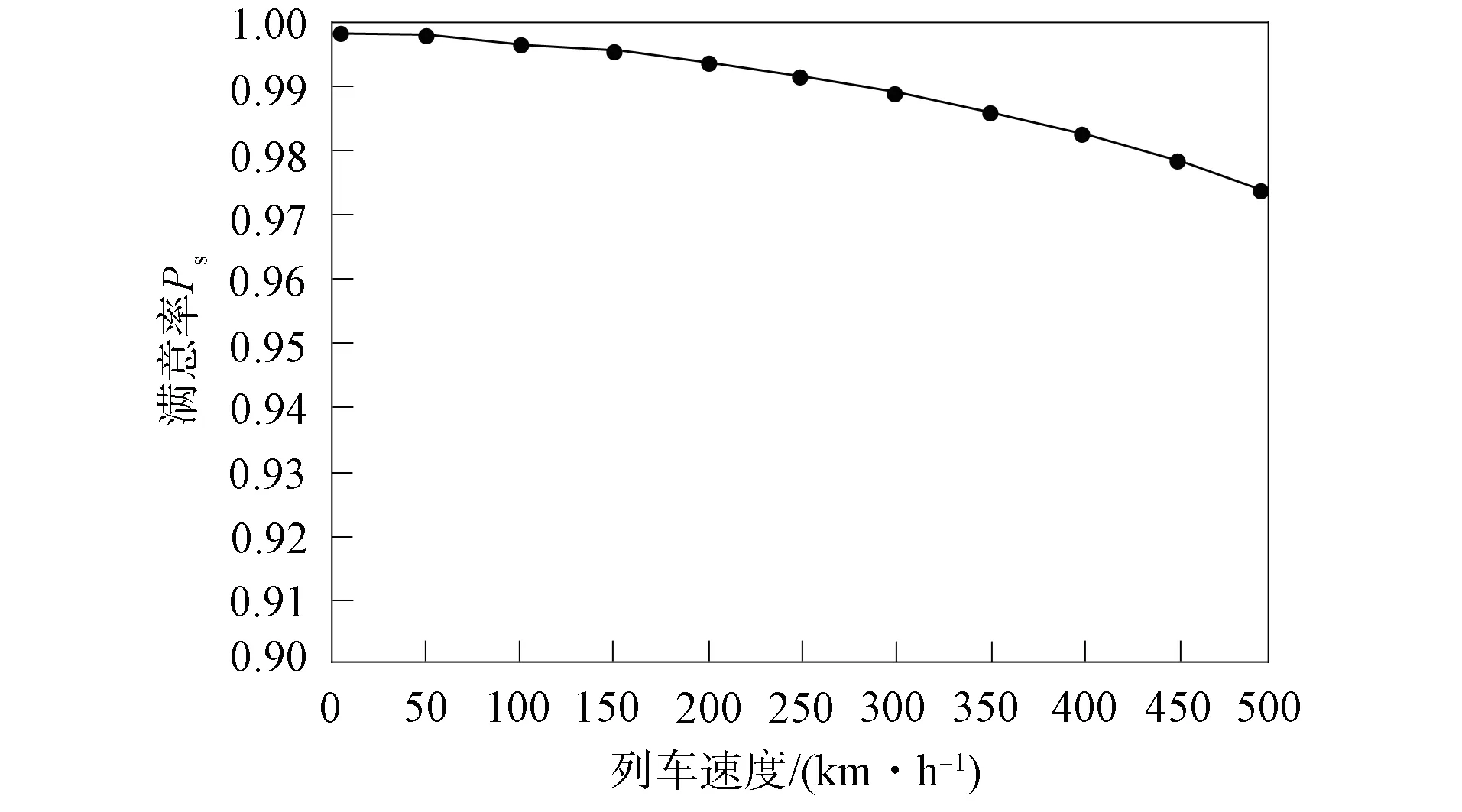
图5 速度-满意通信概率的关系Fig.5 Relationship between speed and satisfactory communication probability

图6 不同算法最优信道选择比率的对比结果Fig.6 Comparison results of optimal channel selection rate by different algorithms

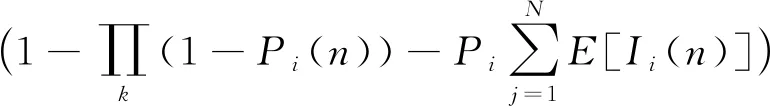
3种算法的成功传输率如图8所示. 由图8可见：随机选择算法的成功传输率最低，约为49.8%；原始UCB算法的成功传输率随时隙t的增加而不断增大，当时隙t≈1 400时，成功传输率增加至80%，然后逐渐趋于平缓，最终维持在约86.7%[17]; 而改进UCB算法在时隙t≈1 000时，便能很快达到约90%，由于仿真环境中设置的最大信道空闲概率为0.9,故随着时隙数的不断增大,始终维持在90%. 由于本文设置了信道质量差异因子,缩减了探索信道的数量,因此,在较小的时隙t内便能达到较高的成功传输率.

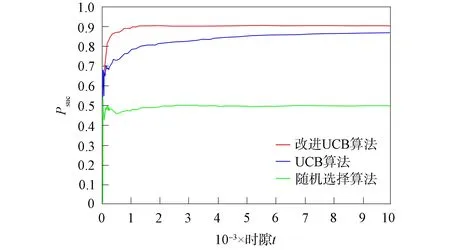
图8 成功传输率Fig.8 Successful transmission rate

综上所述,本文主要研究了高速铁路场景下越区切换过程中的多信道选择问题,分析了基于MAB模型下的多信道选择算法,以UCB算法为基础,设置信道空闲差异因子,算法能快速收敛于最优信道,通过引入SCP衡量移动列车与传输误码率之间的关系；最后分析了本文算法在最优信道选择比率、成功传输率和累积接入损失方面与其他算法的性能关系. 仿真结果表明,本文算法在上述3个评价标准中都有较大的提高,性能更优.