基于改进烟花算法的以太网通信链路调度方法

王宏志,郭嫚嫚,胡黄水,武莎莎

(长春工业大学 计算机科学与工程学院,长春 130012)

近年来,随着列车通信网络结构体系的发展,轨道交通列车正向高速、稳定、舒适化方向发展,因此对列车通信网络的实时性提出了更高要求. 工业以太网[1]以其稳定性、可靠性、实时性已成为工业控制网络领域的研究热点. 但目前的工业以太网技术均采用带有冲突检测的载波监听多路访问(CSMA/CD)技术,没有完备的延迟时间和通信响应,所以合理地安排数据传输过程中的调度问题尤为重要.

目前,智能优化算法及其改进算法被广泛应用于网络调度中. 文献[2]实现了烟花算法径向配电网的爆炸过程组合优化问题,在功率流期间生成网络的适当父节点-子节点路径,提高了配电系统的功率最小化和电压分布；文献[3]提出了一种基于差分进化算子的烟花混合优化算法,结合差分进化运算符(突变、交叉和选择)进行迭代次数的更新,提高了种群的多样性,但某些质量差的组件会导致选出较低的适应度值,影响下一代烟花个体质量；Zheng等[4]提出了一种增强型烟花算法,解决了函数最佳值与搜索空间距离的问题,但未考虑适应度值对选择策略的影响; 文献[5]将改进后的增强型烟花算法应用于高速列车的实际调度中,从新的高斯变异算子----基于生物地理优化的迁移算子(migration operator based on biogeographic optimization,BBO)以及新的选择策略进行改进,增加了调度的多样性,并抑制了过早收敛；Cheng等[6]将改进的具有新爆炸算子和预留策略的多目标返工算法与重新调度烟花算法相结合,以开发方案的开发成本和持续时间及鲁棒性和稳定性为目标函数,提高了算法的稳定性,但增加了算法复杂度. 本文提出一种基于改进烟花算法的实时周期消息任务调度方法(real-time scheduling algorithm based on modified coefficient of variation of fireworks algorithm,CVFWA). 仿真实验结果表明,该算法在降低调度序列传输时延和收敛速度等方面均具有良好的性能.

1 通信链路调度问题建模

1.1 系统模型的建立

为满足数据传输时延的要求,本文系统模型是由1个源主机和3个目的主机组成的工业以太网网络,针对该模型,提出如下假设：

1) 本文的数据调度问题主要针对在源主机和目的主机之间的数据链路,数据类型为实时周期数据;

2) 源交换机发出的数据到达过程均服从Poisson分布,终端交换机接受数据的过程也服从Poisson分布;

3) 在任务开始调度前有足够的时间对数据进行调度规划安排,缓冲区的长度足够大,能容纳所有的传输序列流.

1.2 调度数学模型的建立

针对上述模型的分析与假设,将实时周期消息[7]任务的调度转化为数学模型,可表示为一个三元组：

DPRT={D1,D2,…,DN},i∈1,2,…,N,

(1)

τi=(Ti,Pi,deadi),i=1,2,…,N,

(2)

其中：DPRT表示实时周期数据任务的集合,由N个互相独立的实时周期任务组成；τi表示每个实时周期任务,Ti表示当前任务的周期,Pi表示当前任务的最坏执行时间,deadi表示当前任务的截止期.

基于假设2)可知,数据包的发送过程满足：

(3)

链路传输速率取决于链路信道状态与资源分配策略,因此需满足：

(4)

其中:Cv(τi)表示数据链路的传输速率;θi表示保证目的主机能实现可靠通信的信干噪比,用公式表示为

(5)

式中sij表示为满足数据接收端主机的通信服务质量,在其能从源主机的发送端接收到的二进制比特流中区分出数据帧的起始与终止而对链路设定的信道增益,δi表示源主机端的发送功率,Ip表示接收端导致的噪声干扰,N0表示信道中的背景噪声.

(6)

在时延方面,调度模型存在如下关系：

(7)

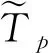
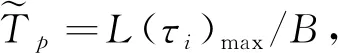
(8)

其中L(τi)max表示实时周期数据中的最大数据长度,B表示被分配的带宽.

综上对实时周期数据传输的分析,基于改进烟花算法的工业以太网通信链路调度方法的适应度函数可表示为

(9)

2 工业以太网通信链路调度算法

2.1 烟花算法

烟花算法[9]是一种新型智能算法,其根据烟花爆炸扩散等现象类比提出. 算法主要包括以下内容：爆炸算子、高斯变异算子、映射规则和选择策略[10]. 对于烟花爆炸的火花数Fi和爆炸幅度Ri,计算公式如下：

(10)

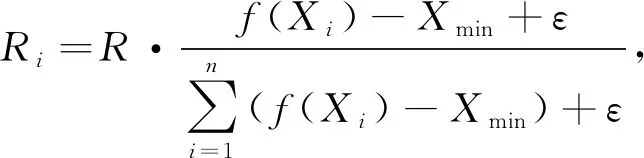
(11)

其中Fi表示第i个烟花产生爆炸火花的数量,f表示产生所有爆炸火花的总个数,其为一个常数,Xmax表示最差的适应度值,f(Xi)表示第i个烟花的适应度值,ε是为防止分母为0设置的一个常数值,Ri表示第i个烟花产生爆炸幅度的范围,R表示最大的爆炸半径,Xmin表示最优烟花个体产生的适应度值.

为使烟花产生的每代都是高质量的火花,需要对爆炸产生的火花数量进行设置：

(12)

其中a和b是常数,取值范围为[0,1],round是取整函数.

完成上述过程后,还需进行高斯变异操作[11],对第k维的任一个火花xi进行高斯变异操作,计算公式为

ΔXi,k=Xi,k×m,

(13)

其中:Xi,k表示烟花在第k维的位置矢量值; ΔXi,k表示烟花个体经过变异后的位置矢量值;m～N(1,1),N(1,1)表示一个能使m服从的均值为1、方差为1的高斯分布.

此外,还需对爆炸后的烟花进行可行解空间的设定,以保证其上下界范围,对于不在范围内的火花重新映射,计算公式为

Xi,k=XL-Bou,k+|Xi,k|%(XH-Bou,k-XL-Bou,k),

(14)

其中XH-Bou,k和XL-Bou,k分别表示第k维中烟花位置i矢量的可行解空间上下界.

2.2 高斯变异算子的改进

考虑到不同维度对变异的期望程度不同,本文在此基础上提出一种新的高斯变异算子,通过引入变异系数描述算子的变异程度,选出变异系数最大的维度进行变异操作. 变异维度选取公式如下：

(15)

其中i表示某一维度,n表示候选烟花的数量,VC表示变异系数,w表示烟花各维度的标准差,α表示烟花维度的均值. 通过上述方法选取将进行变异操作的维度,选择变异系数最大的烟花维度进行变异操作,变异系数越大,表示离散程度越大.

2.3 选择策略的改进

传统烟花算法采用基于“精英-距离”的选择策略[12],通过计算欧氏距离占比概率高低作为选取下一代烟花的标准. 传统烟花算法性能一般,且局部搜索能力较差,尽管还有锦标赛选择策略[13],但单纯依靠该方法会使适应度值出现优劣问题,两端的适应度选择不均衡,存在较大缺陷. 本文针对上述问题,提出一种基于中位数锦标赛的选择策略,操作过程如下：

1) 从总体中选择一定数量的烟花作为候选集参与下一代烟花的个体选择,候选集设为K,个体总数为M；

2) 将每个候选集烟花个体的适应度值按升序的方式排列,取出适应度值的中位数Zn；

3) 选出中位数对应的适应度值,将候选个体分为K1和K2两组;

4) 在3)中的两组候选集中,每组随机选择M/2组候选个体,将每组中的最优秀个体作为下一代爆炸中心.

改进后的选择策略增加了适应度较差个体被选择的概率,增加了种群多样性.

3 工业以太网调度过程

3.1 实时周期数据任务调度编码

为提高实时周期数据任务[14]在烟花算法下调度机制的有效性,利用离散机制进行实时周期数据任务的编码. 待调度的任务数据表示为

Li={τ1,τ2,…,τn},i∈N,

(16)

其中i表示实时周期中数据包的序号,τi表示任务的序列. 通过烟花算法合理安排任务调度序列,使工业以太网数据链路上的数据包到达时间达到最小值.

3.2 调度过程

步骤1) 设置烟花算法中的参数,包括任务数量N、待调度的任务数据Li、爆炸火花数量Fi、爆炸幅度Ri和最大迭代次数I等；

步骤2) 根据3.1中的任务调度编码方法,初始化烟花位置并将烟花位置转化成实时周期数据的调度序列；

步骤3) 计算当前位置的烟花个体及其目标函数值,并统计当前最优位置及函数值；

步骤4) 产生爆炸火花,并根据式(10)～(12)计算其爆炸数目和爆炸范围；

步骤5) 产生高斯变异火花,先根据2.2的改进方法计算并选取变异维度,再根据式(13)进行变异操作,按式(14)对超出范围的烟花重新映射到范围内；

步骤6) 根据2.3提出的方法计算中位数锦标赛选择策略下的下一代烟花个体,检验是否达到最大迭代次数,若未达到则返回步骤3),令iter=iter+1,直至找到最优烟花序列,算法结束,输出最优函数值.

改进烟花算法流程如图1所示.

图1 改进烟花算法流程Fig.1 Flow chart of improved fireworks algorithm

4 仿真分析

图2 不同算法调度序列适应度与迭代次数的关系Fig.2 Relationship between scheduling sequence fitness and number of iterations of different algorithms

在MATLAB 2016a环境下,搭建通信链路调度模型,设从源主机到目的主机的通信链路中,烟花群规模为20,维度为10,爆炸火花个数为40,爆炸半径为40 m,爆炸数目限制因子a=0.3,b=0.6,变异火花数为10个,变量上下界为[-10,10],最大迭代次数为50次,调度任务数量为10,源主机的信干噪比需求为8 dB. 仿真实验中,本文将烟花算法(FWA)和基于锦标赛选择策略的烟花算法(LoTFWA)与改进后的烟花算法(CVFWA)进行性能比较.

图2为不同算法获得调度序列的适应度值与迭代次数的关系. 由图2可见,相比于烟花算法(FWA)和基于锦标赛选择策略的烟花算法(LoTFWA),本文的改进烟花算法(CVFWA)收敛性更优,有效降低了网络中的传输时延. 图3为不同算法数据链路的传输速率与迭代次数的关系. 由图3可见,在保障链路数据正常通信的情况下,CVFWA算法相比于FWA算法和LoTFWA算法传输速率更快,有效提高了链路数据通信的实时性能. 图4为由不同算法获得源主机的信干噪比与迭代次数的关系. 由图4可见,FWA算法的信干噪比不能满足本文所设定的信干噪比值,所以源主机与目的主机之间的链路无法实现数据通信. LoTFWA算法虽能满足设定要求,但没有CVFWA算法效果好,因此,CVFWA算法更能满足本文设定的信干噪比参数的要求,实现节点之间的可靠通信.

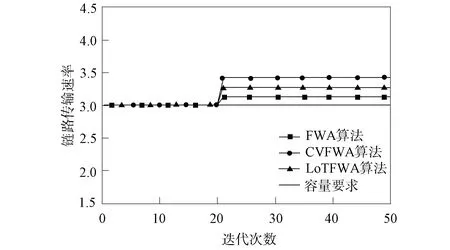
图3 不同算法链路传输速率与迭代次数的关系Fig.3 Relationship between link transmission rate and number of iterations of different algorithms

图4 不同算法源主机信干噪比与迭代次数的关系Fig.4 Relationship between SINR of source host and number of iterations of different algorithms

综上所述,本文在传统烟花算法的基础上提出了一种基于改进烟花算法的以太网通信链路调度方法,增加了对变异维度的选取,同时将选择策略改进为中位数锦标赛选择策略. 仿真实验结果表明,在保障链路数据正常通信的情况下,CVFWA算法不仅有效降低了节点间链路数据的传输时间,而且加快了节点间链路数据的传输速率,提高了节点间链路数据通信的可靠性,在一定程度上保持了链路通信的实时性.