核心素养视角下对中考数学方向的研判

陈益民

[摘  要] 对核心素养背景下的中考数学方向的研判，应当从关键能力、思维品质等角度进行;核心素养对中考数学的引导作用可以从理论与实践两个角度来判断与分析. 核心素养视角下的中考数学走向，要抓住两个关键点：一是对课程标准的理解，二是对已有中考试题的研究. 在核心素养背景之下研究中考数学的走向，很关键的一点就是在中考数学优秀传统的基础上，思考核心素养存在的空间，然后进一步思考如何结合传统去进行核心素养的评价.

[关键词] 中考数学方向;核心素养;初中数学;教育教学

核心素养的培育离不开一个关键的话题，即考试评价. 对于初中数学，中考数学是日常教学最有效的指挥棒，这根指挥棒指向哪里，教师的教学就会走向哪里. 因此一个基本的判断就是：在中考数学中核心素养有怎样的体现，日常教学中数学学科核心素养的培育就会有相应的途径. 坦率地说，初中数学一线教师最为关注的就是中考数学的方向. 虽说中考方向是由课程专家以及命题专家决定的，但是一线教师在教学的过程当中，如果对核心素养背景之下中考数学的方向有一个基本的研判，那教师对自己的教学就有一个基本的认识，就知道如何在日常教学当中去寻找恰当的核心素养培育路径.

站在数学的角度看核心素养，结合中国学生发展核心素养的基本判断，数学核心素养可以理解为具有数学基本特征的、能够适应学生终身发展和社会发展需要的必备品格与关键能力. 显然，数学學科核心素养是数学课程目标的集中体现，是在数学学习的过程中逐步形成的、由思维品质支撑的各种能力的总和. 因此人们一般又认为，数学核心素养不仅包含外显能力，还包含内在思维品质，进而，对核心素养背景下的中考数学方向的研判，也应当从关键能力、思维品质等角度进行. 至于必备品格，并不适宜用量化的方式进行评价，故不在本文的阐述范围之内.

核心素养对中考数学的引导作用

核心素养具体到数学学科当中所表现出来的数学抽象、逻辑推理以及数学建模等要素，其必然有两点内涵：一是一定时期内（一学期、一学年或者三个学年）的学科教学中应当有核心素养培育的目标，二是日常的教学当中应当有核心素养培育的意识. 因此，核心素养对中考数学的引导作用是不言而喻的，这种引导作用可以从理论与实践两个角度来判断与分析.

从理论的角度来看，教师对核心素养的理解要从定性角度走向定量角度，要将核心素养的理论阐述转化为具体的可测量的评价因素. 很显然这不是仅依靠数学学科核心素养组成要素就能够实现的，其必然会结合传统数学评价的基本思路，必然要将数学学科核心素养的组成要素转化为具体的问题解决或习题解答中的学生思维过程. 只有这样才可将其量化，变得可测量.

从实践的角度来看，要理解核心素养的引导作用，一定程度上需要教师认识到传统中考中核心素养的缺失，需要教师思考核心素养如何在具体的数学题中得到体现. 只有为核心素养找到具体的载体，尤其是以可评价方式存在的载体，那对核心素养的评价才有据可依. 由于核心素养的培育是当前初中数学教学的必然任务，因此核心素养对中考数学的引导，也就体现在教师对评价方式（试题）的研究与编制上.

将理论与实践结合起来，可以建立核心素养视角下中考数学的宏观理解. 比如说，某省依据《义务教育数学课程标准（2011年版）》，在中考数学试题的编制上强调突出考查学生数学核心素养和学习能力，强调面向全体学生，重视有效评价，关注数学文化价值和数学阅读，考查开放与探究、数学建模、综合与实践. 通过这样的努力，就可以在中考中了解不同学习水平的学生真实的数学学习状况，这对初中数学教学改革能够起到积极的指导和引领作用. 应当说这样的判断，对于核心素养引导中考数学走向以及如何在中考数学中体现核心素养，有着积极的作用.

核心素养视角下的中考数学走向

基于上述分析，思考核心素养视角下的中考数学走向，要抓住两个关键点：一是对课程标准的理解. 当前面向初中数学学科核心素养的课程标准还没有正式发布，但是结合《义务教育数学课程标准（2011年版）》中提出的十个“核心关键词”，即数感、符号意识、空间观念、几何直观、数据分析观念、运算能力、推理能力、模型思想、应用意识和创新意识，也可以认为这是具有“初中学段特色”的数学核心素养组成要素. 二是对已有中考试题的研究. 中考题都是命题专家呕心沥血之作，其能够较为全面地体现传统数学教学评价的需要，在此基础上思考其与数学学科核心素养的结合点，既能够体现核心素养的引导作用，也能够对核心素养背景下初中数学中考的走向进行一个比较准确的评价.

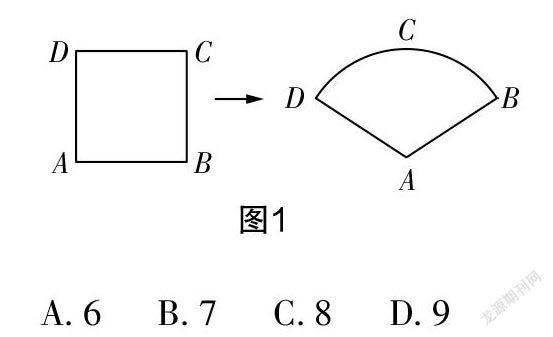
例如有这样一道中考原题：某数学兴趣小组将边长为3的正方形铁丝框ABCD变形为以A为圆心、AB为半径的扇形，则所得到的扇形DAB的面积是（    ）

A. 6    B. 7      C. 8      D. 9

从传统评价的角度看这道题目，其考查的是平面几何中的面积计算，从数学知识掌握与运用的角度看，学生要解决这道题目难度并不大. 那么如果从核心素养培育的角度，看这道题目所用到的素材以及题目编制，笔者认为有两个思路：一是题目中从正方形向扇形的转变，可以在生活当中找到相关的原型，利用相关的素材，给出实际生活中的情境，这样就可以培养学生的数学抽象与数学建模能力;二是就原题的解题思路进行挖掘，让学生在解题思路优化的过程当中，评价学生的逻辑推理能力.

对于第一个思路，一个简单的试题命制可以是这样的：小明想将一个边长为3的正方形纸板剪出一个扇形，那所得到的扇形的最大面积是多少？很显然学生在面对这个问题的时候，需要在大脑当中进行想象，以构建一个表象，这一过程中，学生会发现一个正方形纸板可以剪成无数个扇形，但最大的扇形出现在其半径等于正方形边长的时候. 这样就有一个数学抽象的过程，同时也是运用正方形和扇形模型的过程，具体不再赘述.

对于第二个思路，可以考虑在命题的时候改变题型，让学生通过逻辑推理也就是计算或证明的方式来解答问题. 这里涉及的其实是正方形去除一个最大扇形之后剩余图形的面积，如何转化为半径为正方形边长的扇形面积的问题. 对于这一问题的解决，还可以进一步运用逻辑推理的方法，这里要注意的是正方形的周长和扇形的周长相等，在这一前提之下进行切换，是问题解决的关键. 认识到这一点之后，就可以有效地借助这一问题来评价学生的逻辑推理能力.

努力让核心素养发挥“指挥棒”作用

通过上述例子可以发现，在核心素养背景之下研究中考数学的走向，关键的一点就是在中考数学优秀传统的基础上，思考核心素养存在的空间，然后进一步思考如何结合传统进行核心素养的评价.

由此判断中考数学的走向，在当前可以预期的范围之内，中考数学要体现出核心素养，肯定不可能脱离已有的传统另起炉灶，而应当在继承现有中考数学主要功能的基础之上，努力体现出数学学科核心素养的价值. 笔者上述分析的主要思路，实际上就是对已有中考题目进行适当的改造，以使其能够体现出核心素养. 真正的中考数学命题，应当拓展更加新颖且切合初中学生认知实际的题材，将数学学科核心素养的要素渗透其中，然后形成一道既具有评价选拔功能，又具有核心素养引导功能的试题. 当然，这是一个循序渐进的过程，一份试卷上传统习题与具有核心素养评价功能的习题同时存在，应当是当前中考数学试卷的基本样态. 认识到这一点，有助于教师在日常教学当中更好地把握知识教学与核心素养的培育.

总体而言，核心素养是当前教育领域的热词，被誉为当代基础教育的DNA，且未来基础教育的顶层理念是强化学生的核心素养. 对核心素养这种作用的认识，既应当体现在理论上，更应当体现在实践中，尤其是对于一线教师而言，既要进行理论的学习，又要进行实践的探索，只有这样才能更快地实现核心素养的落地.

3243501908202