课堂练习的现状与设计策略研究

董伟丽

[摘  要] 课堂练习不仅能巩固新知，还能反馈课堂教学效果，发展学生的数学能力. 文章从教师对课堂练习的认识、理解层次与时间把握三方面谈课堂练习的现状，并提出设计课堂练习的策略：设计趣味性练习，唤醒学生的学习热情;设计探究型练习，培养学生的创新意识;设计开放型练习，激活学生的数学思维.

[关键词] 课堂练习;认识;思维

课堂练习不仅能检查课堂教学成效，还能促使学生强化与巩固所学知识. 拓展类的课堂练习还能充盈、丰富课堂教学内容，提高学生的思维能力，增加学生的知识积累. 新课标明确提出，要让人人学有用的数学，这就要求我们要做到学以致用. 而课堂练习能让学生从数学的角度对生活中的现象产生思考，从而对数学学科产生浓厚的兴趣.

课堂练习的现状

放眼当下，初中数学课堂练习的现状令人担忧. 一些教师不论是在思想认识上，还是在行动上，都对课堂练习抱着可有可无的态度. 部分教师认为，学生只要理解了教学内容就行，至于课堂练习，完全可以用课后作业代替;还有教师认为课堂练习就是浪费时间，还不如多讲一道例题来得实在. 为此，笔者将教师在课堂练习方面存在的一些不足归结为以下几点.

1. 认识不够全面

教材或教辅资料提供的习题是练习的范例，针对的是大众，而课堂练习是小范围的针对本节课的特点而设计的. 因此，我们应根据教学内容与学生的具体情况，设计具有一定针对性与挑战性的习题，让学生从这些量身定制的课堂练习中获得进步.

有专家分别对农村与城镇各个年龄层次的教师展开过调查，发现有72%的教师不会自己设计课堂练习，而是直接运用教材或教辅资料上的原题进行课堂练习，有21.6%的教师会稍微改动原题，只有6.4%的教师采用自编习题的方式. 其中城镇年轻教师创编习题的情况多于农村年龄偏大的教师.

2. 层次理解不够

人类的认知均遵循由浅入深、由易到难、循序渐进的原则. 学生之间均存在个体差异，他们在知识的接受能力上也存在显著差异. 因此，课堂练习的设计应尽可能地照顾到各层次水平学生的需求.

从当前课堂练习的现状来看，大部分教师没有关注课堂练习的层次性，同一节课基本都使用同一套课堂练习，抑或平铺直叙的练习. 这些练习方式都有悖于学生认知的发展. 所有的学生做同一份练习，会出现“学困生吃不下，学优生吃不饱”的情况，久而久之，难免会挫伤学生学习的积极性，从而难以达到练习的预期效果.

3. 时间把握不准

受传统思想观念的影响，当前仍有部分教师认为多做题对学生成绩的提高必然有很大的帮助，因而出现囫囵吞枣地授课，同时大搞题海战术的现象. 这部分教师主张的教育理念是：多练总比少练好. 其实，课堂练习的时间掌握在10～15分钟最合理. 因为学生的注意力有限，在经历半小时的授课后，很大一部分学生已经处在思想开小差的边缘. 此时，课堂练习能重新激发学生的活力，让学生将注意力转移到练习中.

课堂练习时间过短，学生无法展开思考;但课堂练习时间过长，必然会影响授课进度. 因此，一定时间范围内的练习能为学生提供思考的空间，学生也会在日复一日的课堂练习中养成良好的思考习惯.

课堂练习的设计策略

课堂练习是数学课堂教学中不可或缺的组成部分，学生能在丰富的课堂练习中开阔视野，充盈知识，提高学习效率. 鉴于此，笔者近年一直置身于课堂练习的设计研究中，总结并提炼出了以下几种策略，供读者参考.

1. 设计趣味性练习，唤醒学生的学习热情

兴趣是学习最好的老师，它能促使学生的学习态度积极，是推动学生学习的内驱力. 教师设计富有趣味性的课堂练习，能给课堂带来生机与活力，从而唤醒学生的学习热情，让学生从不同的角度去分析问题并解决问题.

案例1“相似三角形的性质”课堂练习.

为了激发学生对教学内容的兴趣，教师在课堂练习中设计了这样一道题：

学期伊始，班主任准备给班上的同学排座位，于是要求所有的学生到阳台上按照由矮到高的顺序排队. 小明和小辉都觉得自己比较高，争得面红耳赤. 老师说：“你们两个各自站好，请一位同学来量一下地上的影子，根据影子的长短就能判断你们谁高谁矮了. ”聪明的你，能不能用所学知识解释一下老师的判断是否有依据？为什么？

这一课堂练习其实是一个问题情境，此情境是学生所熟悉的或亲身经历过的生活场景. 这样的练习比枯燥、单一的练习生动、有趣，学生在富有趣味性的问题情境中分析、思考，解题也变得更有乐趣. 这种方式能有效地喚醒学生的学习热情，同时，学生在问题的解决过程中还深化了对相似三角形性质的理解.

2. 设计探究型练习，培养学生的创新意识

数学是思维的体操. 社会的发展需要创新型人才，而创新能力的培养需要从教学的点滴做起. 课堂练习作为数学课堂教学不可分割的一部分，自然也担负着培养学生创新能力的责任. 因此，教师设计课堂练习时，应针对性地增加一些促进学生能力发展的探究型练习. 学生在此类练习中会突破思维定式，激发分析问题的潜能，从而产生创新意识.

案例2“等边三角形”的课堂练习.

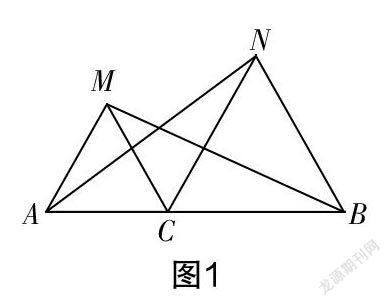
如图1，△AMC与△BNC都是等边三角形，C是线段AB上一点.

（1）求证：NA=MB.

（2）将△AMC绕点C逆时针旋转180°，点A落在线段CB上，试画出旋转后的图形，并判断此时NA与MB是否相等.

（3）将△AMC绕点C逆时针旋转一定的角度，NA=MB还成立吗？假如成立，请证明;假如不成立，请说明理由.

此练习由浅入深地深化了所学内容. 学生在解题时，需开动脑筋，通过观察、分析、猜想、实验与推理等过程，不断探索问题的答案. 此类题不仅能强化学生对所学知识的理解，还能提升学生的数学思维，践行新课标所倡导的培养学生养成实践、探索与创新的科学精神.

3. 设计开放型练习，激活学生的数学思维

新课标强调学生是课堂的主人，要让学生在实践与探索中加强同伴间的合作与交流，形成良好的数学思维. 开放型练习具有答案不唯一的特点，能有效地考查学生分析问题与解决问题的能力. 学生在问题的探究中，发挥自身的长处，与组内成员协同合作、共同进步. 学生的思维也在这良好的学习氛围中被激活，这对提升学生的数学核心素养来说具有重要的作用.

案例3  “勾股定理”的课堂练习.

已知，在△ABC中，将∠A，∠B，∠C所对的边分别称为a，b，c，其中a，b的长分别为3和4，则第三条边c的长是多少？

不少学生见到此题，便毫不犹豫地回答“5”.

师：为什么c的长度是5呢？

生：由勾股定理很容易就得到c=5了.

师：勾股定理是针对什么三角形而言的？

（学生恍然大悟）经过讨论与探究，学生得出了以下结论：①若∠C为直角，则c的长为5;②若∠B为直角，则c的长为;③本题中，∠A不可能是直角;④c的取值范围是1

学生在这道开放型问题的引导下，再次强化了对勾股定理的理解，并在交流中进行思考与分析，有效地激活了数学思维，提升了对这部分知识的学习兴趣. 开放型练习的设计，为发展学生数学思维的广度提供了较好的平台，学生也在积极思考与探究中获得了可持续发展.

总之，课堂练习作为课堂教学的重要组成部分之一，需要教师精心设计符合学生实际水平的练习. 教师应鼓励学生在生动有趣、具有探究性与开放性的练习中，构建新的知识结构，提升自己的认知水平，从而促进各种能力的提升.