立德树人,学大于教
郁烨


[摘 要] 立德树人是中国教育者亘古至今的使命,更是新时代教育人的担当. 狭义地说,“德”即德育,德育是教育的根本任务,也是“树人”的前提和保障. 教育立何德?树何人?南通市“立学课堂”以日常教学的实践研究为出发点,对这个问题做了回答. 总的来说,立学课堂是以“限时讲授、合作学习、踊跃展示”的原则为指导,重点关注学生的“学”而非教师的“教”,从“立人”“立根”“立身”三个维度打造以学为主的课堂.
[关键词] 立德树人;初中数学;立学
笔者从事初中数学教学多年,深深感受到了“立学课堂”对教学带来的改变,下面结合常态课“图形的相似”(人教版九年级下册)的教学片段,就如何将立学课堂落实到日常教学中谈谈自己的理解.
立人:秉持人格,自然伸展
“立学”,即“立人之学”,也就是对“树何人”的回答. 众所周知,教育培养的是人类的未来,将学生培养成有健全人格的、适应社会发展的人是新时代教育的担当. 学生是一个完整的人,是一个有多样化特征的人,因此立学课堂倡导教师在课堂教学中要基于学生的个性而展开,要尊重学生的人格,避免出现“目中无人”的教学现象.
【创设情境,引入教学】
数学新授课常常由情境教学来引入,情境的创设要适宜学生的身心及个性,并以此激发学生主动学习的热情,体现“立人”的本质.
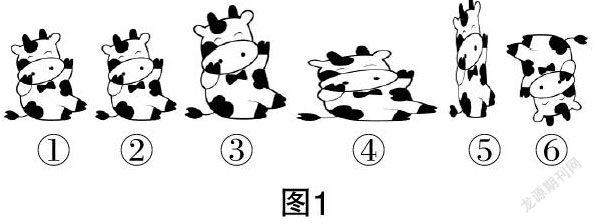
师:观察图1所示的①②两个图片,它们是什么关系?
生1:它们是全等图形.
师(追问):什么是全等图形?
生1:形状和大小都相同的图形是全等图形.
师:那么图片②和图片③是全等图形吗?
生2:不是,它们的形状相同,但大小不同.
师:你观察得很仔细. 你所说的两个图形之间的关系是本节课的主题,我们称之为相似图形.
【教师揭示课题:图形的相似】
师:你们能用数学语言描述一下你们对相似图形的理解吗?
生3:相似图形就是形状相同但大小不相同的图形.
师:图片①和图片②是相似图形吗?
生(齐):是.
师:图片①和图片⑥呢?
生(齐):是.
师:图片④、图片⑤和图片①呢?
生(齐):不是.
(教师眼光转向生3,示意其更正自己的回答)
生3:相似图形就是形状相同的图形.
生4:相似图形可以看成是由原图形放大或缩小得到的.
设计意图 以有趣的卡通图片引入教学,一方面能吸引学生的无意注意,让他们主动参与到课堂学习中;另一方面,能让抽象的数学定义变得生动形象,能降低学习难度,给学生树立学习本节课内容的信心.
引入环节是课堂的“开场”,也是调节课堂气氛、引领学生学习最重要的环节之一. 在这个过程中,教师应关注引导而非灌输,应让知识自然伸展而非预设,应根据学生的特点及需要展开教学,同时允许学生之间存在差异,体现“立人”的根本.
立根:明晰目标,变教为学
立学也是“立根之学”,“根”即“根源”. 教学的任务是让学生明确为什么学、如何学、学多少,在明确目标的基础上将“教”变成“学”,激发学生的主动性和自主性.
【共同探究,提出猜想】
共同探究包括师生及生生的共同合作,共同创造一个学习共同体,在良好的氛围中对知识提出猜想,让学习变得主动.
师:我们接下来主要研究相似多边形. 如果多边形可以移动操作,你将怎样判断它们是否相似?
生1:我会将图形放大或缩小后进行比较.
师:如果多边形呈现在纸上,是静态的,无法移动,你将研究这两个多边形的哪些元素?
生2:我想去研究它们的内角及边长.
师(追问):你是怎么想到这两个元素的?
生2:我类比了全等三角形的判定方法.
师:那你的猜想是?
生2:对应角相等的两个多边形相似.
设计意图 师生平等对话,教师鼓励学生说出自己的想法,并在此基础上引导学生利用类比的方法猜想多边形相似的条件,为接下来的验证环节做铺垫.
【验证猜想,形成定理】
验证猜想是每节数学课的重要任务,只有通过已有知识经验证正确的猜想才能形成定理. 由猜想到验证也是数学核心素养中逻辑推理能力的体现.
任务1:探究怎样的两个多边形可以称为相似多边形.
(完成方式:以小组为单位,组员先独立思考,然后经组长召集分享个人观点,讨论达成共识后小组代表交流展示)
展示片段如下.
组1:我们小组提出了两个观点,一是只满足角相等的两个多边形相似;二是同时满足角相等及边成比例的两个多边形相似. 第一个观点最终被否定,所以我们的最终观点是“角相等、边成比例的两个多边形相似”.
师:你们是如何将第一个观点否定的呢?
生1:我們是通过举反例的方式进行否定的. 正方形和矩形的角相等,但它们不相似.
生2:我还有要补充的,首先,相似多边形的边数要相等.
教师对学生的回答表示赞同与赞赏,然后归纳相似多边形的文字语言、图形语言及符号语言.
设计意图 相似多边形定义的探索是本节课的重点,学生需要自己完成这部分知识的建构. 探究相似多边形的定义时,笔者采用的是小组活动的方式,因为一方面能调节课堂气氛,另一方面能加深学生对该知识的印象.
在数学学科教学中,“立根”更多地体现在知识的生成过程中,让学生知其然,更知其所以然,主动参与,教师则归还课堂主权,有意识地减少自己讲授的时间,鼓励学生合作学习、踊跃展示,关注学生的学习. 立学课堂倡导学生真正参与学习,经历知识的生成过程,重视过程.
立身:合作探究,教学相长
立学更是“立身之学”,更多地倾向于为人处世之道,即教师用自己的人格魅力去感染学生,让学生受到潜移默化的影响. 在这个过程中,教师“挺直身子”是前提与必要条件,因为“跪着教书”的教师绝不可能教出顶天立地的学生.
【剖析定理,内化知识】
由对定理中文字的剖析与解读,达到对知识的内化,这是几何定理学习常用的方法,也是学会运用定理的前提与保障.
任务2:(议一议)边数相同的正多边形相似吗?如果不相似,请举出反例;如果相似,怎么表示它们的相似比?
(完成方式:学生独立思考,踊跃发言)
生1:边数相同的正多边形相似,因为边数相同的正多边形的形状是相同的.
师:没错,你是从相似图形的定义出发解答这个问题的.
师:非常棒,你的思维真严密.
师(追问):我们如何表示两个相似正多边形的相似比?
生(齐):边长之比.
设计意图 数学知识的习得往往建立在对知识的深入认识之上,因此,教学时,教师可在呈现定理之后让学生自己思考,让他们对所学定理进行剖析与迁移,以此加深他们对该内容的认识.
【应用定理,解决问题】
在几何学习中,文字是基础,问题是实践,学是为了用. 运用所学知识解决实际问题是数学课堂的高潮环节,也是学生学习知识的最终目的.
试题2:如图2所示,已知五边形ABCDE与五边形A′B′C′D′E′相似. 在五边形ABCDE中,AB=12,ED=18,∠A=85°,∠D与∠A互补;在五边形A′B′C′D′E′中,A′B′=14,∠B′=∠E′=115°,求E′D′的长度及∠C的度数.
(完成方式:学生独立完成后全班交流、展示)
设计意图 两道试题的设置分别是对相似多边形判定及性質的实际运用. “试题1”属于文字题,其能强化学生的画图意识,培育其数形结合核心素养;“试题2”是对相似图形的性质及多边形内角和定理的运用,旨在让学生利用本节课所学知识解决问题的同时,感受知识之间的相互联系.
“行是知之始,知是行之成.”知识的传递与行动的引导是相互依存、相辅相成的,“行”就是“立身”的直接体现. 教师在课堂上的“行”渗透在教学的每一个环节,并时刻影响着学生,让学生在学习中不盲从、不迷信,自己成为课堂的主人,成为知识的主人.
立学课堂在教学中是一个总的指导体系,没有固定的教学范式,但是用心观察会发现,它的指导方针在每节课上都有所体现. 作为一线教师,我们需要用自己的实践来领悟立学课堂的精髓,用行动来诠释立学课堂的真谛,只有这样,方能让“教”转变为“学”,体现立德树人的本质.
3959501908228

