谈整体观视角下的深度学习

李晓苗 易良斌

[摘  要] 在教学中，教师们常困惑于如何设计与组织教学，让真正的学习发生. 文章借助实践中的案例，谈一谈如何在整体观视角下设计教学，从而在问题中深度思考、在活动中深度体验、在项目中深度学习，充分发挥数学内在力量开展深度学习活动，使学生学会数学知识的同时，学会数学地思考问题和解决问题，从而真正地学会学习.

[关键词] 深度学习;整体观;项目制活动;问题情境

深度学习是当前数学教育研究的热点之一，许多教师都认识到了深度学习的重要性，但对于如何设计与组织教学，让真正的学习发生，常常充满困惑. 深度学习是指，在教师的引领下，学生围绕具有挑战性的数学学习主题，全身心积极参与、体验成功、获得发展的有意义的数学学习过程. 深度学习的教学设计重点是，通过精心设计问题情境和学习任务，引发学生的认知冲突，组织深度探究的学习活动. 在具体的教学中，我们可以从整体观视角下设计教学，引导学生关注整体框架，在一般观念的引导下充分发挥数学内在力量，开展深度学习活动.

下面以“特殊平行四边形复习与探究”教学为例，具体谈一談教学中如何从整体观视角下设计问题和活动，并组织深度探究，开展深度学习.

在问题中深度思考

深度学习是基于知识的内在结构和整体特性，以问题为主线、知识为载体，引导学生从知识学习走向思维发展. 在课堂教学中，我们不妨采用以问题引导学习的方式，激起学生主动思维、深度思考. 而要采用这样的方式，问题的设计尤为关键.

在教学中，我们不妨从整体观出发来设计问题，以逐步培养学生的系统思维. 具体在本堂课中，教师可以从问题“类比三角形怎么研究四边形”到问题“类似地，我们应怎样研究平行四边形”，引导学生归纳及概括研究几何图形的“基本套路”，如一般的研究路径、研究对象和研究方法，结构性地再认识四边形、平行四边形. 再到问题“你能用类似研究平行四边形的方法研究特殊平行四边形吗”，引导学生体验运用研究几何图形的“基本套路”研究特殊平行四边形，建立平行四边形、特殊平行四边形的相关知识联系，形成知识结构网络图，完整地认识特殊平行四边形. 接着，通过“类比平行四边形的研究，你能尝试研究特殊的四边形——梯形吗”，引导学生自主运用研究几何图形的“基本套路”系统性地研究几何图形——梯形. 学生通过类比、推广、特殊化等方法发现和提出梯形中值得研究的问题，并借项目制活动开展深度探究、深度学习，掌握研究几何图形的本领，培养系统思维，提升发现问题、提出问题和解决问题的能力.

在活动中深度体验

从现代认知心理学的观点来看，学生只有在成功与失败的亲身体验中才能真正领悟和掌握所学知识、方法的精神实质. 因此，在教学设计中，教师不妨多设计一些活动，促体验、生思考，让学生在充分经历过程的基础上自然开展深度学习. 值得一提的是，在以往的平行四边形、特殊平行四边形知识整理环节，教师常常借助表格填写来引导学生整理、复习平行四边形的相关知识，学生往往还没开始思考与尝试便被表格带着走. 试问，学生若没有真尝试，没有时间进行系统思考，没有深度体验，那何来深度学习？因此活动的设计尤为重要.

在本节课的知识整理环节，首先，对于问题“怎样研究平行四边形”，教师可借助活动“你能代表平行四边形来个自我介绍吗”来引发学生思考与尝试. 在学生尝试的过程中，教师可借助系列追问“某同学从边的角度介绍了平行四边形的判定，其他人还有补充吗”“研究平行四边形时，除了可以研究它的判定，还可以研究什么”“请大家再想想，你还会怎样介绍平行四边形”，引导学生在活动中尝试系统化地介绍平行四边形. 接着，师生通过归纳、概括（包括借助表格）形成知识结构，使学生的思维深度参与到数学知识的建构中. 学生会在这样的尝试体验中充分经历归纳及概括研究几何图形的“基本套路”，如研究路径、研究对象和研究方法，为后续尝试系统化地研究特殊平行四边形奠基.

其次，对于学生易混淆的特殊平行四边形的判定，教师则可以通过小组活动“借四边形的关系图说一说各种特殊平行四边形分别有哪些判定方法”，让学生在辨析中结构化整理判定方法. 特别地，可让学生在小组讨论中辨析、在小组间互评中辨析、在全班交流中辨析，从而深入理解特殊平行四边形的判定定理及其关系，并在活动中体会怎样研究特殊平行四边形，最后形成知识结构网络图，整体结构化地认识特殊平行四边形，为后续自主运用研究几何图形的“基本套路”系统化地研究几何图形——梯形做铺垫.

【教学片段1】

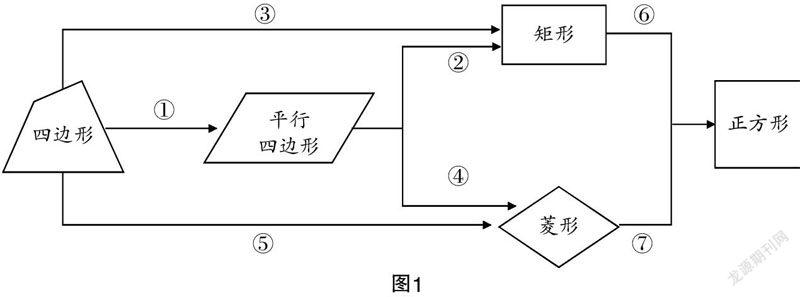
问题1：借四边形的关系图（如图1所示）说一说各种特殊平行四边形分别有哪些判定方法.

（教师为每个学习小组准备了可移动白板和充足的蓝色笔、红色笔、白板笔）

小组合作要求：（1）借助工具袋中的几何图形和磁力扣，在白板上构图;（2）用蓝色笔在白板上完成填空，注意合理分工，力求填写完整、 准确（限时5分钟）;（3）用红色笔为其他小组补充（即评价其他小组，用时2分钟，第1小组评第2小组，第2小组评第3小组，第3小组评第4小组，第4小组评第5小组，第5小组评第1小组）.

（图2～图4展示的是学生进行小组合作）

师生活动：（小结）一起欣赏各组的白板展示，并在辨析中深入理解.

师（追问）：第1小组还加了一个命题“对角线互相平分且相等的四边形是矩形”，你们赞同吗？为什么？第2小组还加了一个命题“对角线互相平分且垂直的四边形是菱形”，你们赞同吗？为什么？

问题2：类比平行四边形的研究，说说几何图形的研究路径、研究对象和研究方法.

师生活动：构建四边形的相关知识结构（如图5所示）.

师（追问1）：研究四边形，特殊化后得到了什么？

生（齐）：平行四边形.

师（追问2）：怎样特殊化平行四边形可得到矩形？怎样特殊化矩形可得到正方形？类似地，也可以从平行四边形出发，先特殊化边得到什么？再……

生（小结1）：研究问题时，类比、推广、特殊化等方法是获得研究成果的常用方法.

师（追问3）：试从对称角度研究平行四边形、矩形、菱形和正方形.

生（小结2）：在探究矩形、菱形、正方形的性质时，我们也可以从对称性角度猜想其性质，再证明，因此研究几何问题时关注图形的对称性会给我们很多启发.

师（追问4）：研究矩形、菱形、正方形这三种特殊平行四边形的路径是什么？具体地，怎样研究它们的定义？如矩形是有一个角是直角的平行四边形，也就是从角特殊的角度来定义矩形的，那菱形呢？我们又该怎样研究它们的性质和判定呢？

师（追问5）：对于任意一个新的几何图形，我们都可以从哪些角度来进行研究？

（师生小结研究几何图形的“基本套路”）

设计意图 从整体的角度回顾平行四边形的研究经验后，教师让学生尝试将其迁移到研究特殊平行四边形. 对于特殊平行四边形的判定以及它们之间的辨析这一难点，教师借助小组合作、小组互评、小组展示的方式得以突破，最后师生合力整理出四边形的相关知识结构，为后续梯形的自主研究做好先行组织者工作.

在这一环节中，学生深度体验了数学基本思想，充分积累了活动经验. 在上述过程中，教师始终引导学生“先独立尝试”，再“交流互动”“总结复盘”，学生在这样的亲身经历中、深度参与中体会和内化了整体观，在迁移中进行深度学习，提高了分析问题和解决问题的能力，为后续的探索、开创做了铺垫.

在项目中深度学习

深度学习的本质是引发学生深度探究. 教师应设计项目制活动，引导学生自主探究，在项目中学会数学地思考，从而体会探究的乐趣、思维碰撞的无限魅力. 显然，高阶思维和创新精神也会在项目制活动中体现.

在项目制活动中，教师首先要用好先行组织者，引导学生通过类比、推广、特殊化等方法发现和提出梯形中值得研究的问题，自主确定研究方向，并运用所学的“基本套路”、方法深度探究，体会几何研究中理性思维的基本过程. 这里值得一提的是，只有前期学生在充分经历中归纳、概括，在深度参与中尝试运用研究几何图形的“基本套路”，才能让自主探究、深度探究成为可能，先行组织者也才能发挥作用;只有前期学生知道了“性质、判定方法是怎么来的”，学生才有机会进一步掌握“发现性质与判定方法”的本领，从而发现问题、提出问题，并进行数学式思考.

其次，在深度探究的过程中，教师要给予学生充分的思维空间和时间. 学生只有充分地独立思考、合作交流，才会有更深度的思考和探究. 如学生在研究梯形遇到困难时，教师鼓励学生提问，通过全班头脑风暴，探寻梯形不同的研究方向;在充分的小组合作交流中，学生深度思考、深度探究;在全班分享中，学生互相启发，带来再次深度思考，在回家作业中、在课外，学生再次进行深度探究. 值得一提的是，探究梯形的性质有一定的难度，教师曾纠结于是否直接给出特殊梯形的概念，引导学生研究特殊梯形的性质以降低难度，但在学生初次独立思考后的交流中，有学生通过画图发现了特殊化梯形的研究方向，于是自然地引出了梯形的分类，并尝试通过画图概括直角梯形、等腰梯形的概念. 这里，学生在自主思考的过程中自然产生问题，这样的问题激发着学生不断地提问与发现，不断地深度思考、深度探究. 这里的深度思考、深度探究离不开学生的独立思考与思维碰撞.

【教学片段2】

（类比平行四边形的研究，尝试研究特殊的四边形——梯形）

师：你们能用研究平行四边形的方法研究梯形这个新的图形吗？请尝试独立思考下面的问题3.

定义：一组对边平行，另一组对边不平行的四边形叫梯形. 其中平行的两边叫梯形的底边，不平行的两边叫梯形的腰.

（1）请画出一个梯形，用字母标出顶点，并指出其中的腰和底边;

（2）你能类比平行四边形的研究，研究梯形吗？

先行组织者1：问题3.

先行组织者2：课件展示前一環节的课堂小结，如图6所示.

设计意图 借助“先行组织者1”“先行组织者2”，一方面引导学生回顾梯形的概念，画图体会梯形的概念，引导学生从概念出发，通过作图、观察、类比、猜想等方式提出梯形的相关命题，然后尝试探寻、推理、论证梯形的性质与判定方法. 另一方面，为学生提供一般观念的指导，引导他们通过类比平行四边形、特殊平行四边形的研究，研究梯形.

师生活动：教师根据学生思考问题3的情况进行追问.

师（追问1）：你们能类比平行四边形特殊化方法，定义特殊梯形（指直角梯形、等腰梯形）吗？

师（追问2）：类比平行四边形、特殊平行四边形的研究方法，你们准备怎样研究特殊梯形？

（给予学生独立思考的时间，让他们提出自己的想法）

师（追问3）：我们可以从边、角、对角线等方面研究特殊梯形的性质，提出你的猜想并证明;也可以提出一条与定义不同的特殊梯形的判定猜想，并证明;还可以类比平行四边形的研究，从边、角、对角线方面来研究一般梯形的性质，提出你的猜想并证明.

小组合作要求：（1）研究梯形，在白板上写出猜想并证明（画出图形，写已知、求证、证明，用时5分钟）;（2）小组展示（可以是猜想、证明或问题，用时2分钟）.

教师引导：可以提出猜想，可以对猜想进行证明. 在证明的过程中，遇到问题时还可以说出你的问题，我们一起探索……

（图7～图9展示的是学生进行小组合作）

在小组活动中，有的小组借助梯形关系图尝试系统化地探究梯形和特殊梯形，提出两底角相等的梯形是等腰梯形，以及当等腰梯形的两腰平行时就变成了平行四边形;有的小组从梯形的定义出发，从角的角度研究一般梯形，还发现了直角梯形有两个直角，并说明了理由;有的小组用表格整理了梯形和特殊梯形共有的性质——上、下两底平行，同一边的上、下两个底角互补，还整理了它们不同的性质——直角梯形有两个直角，等腰梯形上面的两个底角相等，下面的两个底角也相等;有的小组指出，前一个小组发现两底角相等的梯形是等腰梯形，我们发现等腰梯形的两底角相等，但还没想好怎么证明，不过前一个小组的发言对我们很有启发……

师（引申）：今天的课堂对你们有什么启发？关于梯形，你还想继续研究什么？今天的课后作业是整理今天的探究和学习，并完善问题3. 我们的学习和探索，不仅在课堂上，更在课堂外.

设计意图 用研究平行四边形、特殊平行四边形的方法研究梯形，实现研究方法的迁移.

在这样的项目制活动中，教师以数学的发生、发展过程为载体，使学生经历完整的数学思考过程，逐步树立从数学角度整体看问题的观点，逐步掌握数学思考的过程和方法，进而学会数学地认识问题和解决问题. 特别地，在没有正确答案的合作探究中，学生体会到了交流合作的乐趣、思维碰撞的乐趣、深度探究的乐趣，感受到了探究中自己的无穷力量、思维碰撞的无穷魅力. 笔者期待这样的课堂能带给学生未来挑战难度的勇气和力量，期待这样的探究乐趣能陪伴他们勇于挑战更多的未知.

总之，在开展深度学习的教学设计中，教师不妨从整体观视角下设计教学，引导学生充分经历过程，深度体验、深度思考、深度探究，逐步把握数学地认识问题和解决问题的“基本套路”，使学生学会数学知识的同时，学会数学地思考问题和解决问题，从而真正地学会学习.

3478501908267