在“数据的离散程度”教学中感受统计实验活动的乐趣
朱海忠

[摘 要] 以“数据的离散程度”教学为例,创设有助于学生自主探究与合作交流的问题情境,构建统计实验活动,引导学生积极思考、主动探索,让学生在经历统计实验活动的过程中体会刻画数据离散程度的意义,提炼方差的计算公式,领悟方差蕴含的统计思想,积累数学活动经验,增强应用意识,培养数据分析观念.
[关键词] 统计实验活动;极差;平均差;方差;标准差
《义务教育数学课程标准(2011年版)》(以下简称《课标(2011年版)》)将“数据分析观念”作为数学课程的核心概念之一,要求学生对数据统计全过程有所体验,强调发展学生的数据分析观念. 《课标(2011年版)》在统计内容设置上,除了让学生学习一些最基本的统计分析方法之外,更重要的是让学生体会统计的作用和基本思想. 由于统计的学习特别强调学生对统计过程的参与性,要使学生真正理解统计的作用和基本思想,最有效的方法就是让他们真正投入统计的过程中去. 只有在统计活动中,才能利用所学的统计知识和统计方法解决实际问题;只有熟悉统计活动的全过程,才能从整体上理解和把握所学的统计知识和其中蕴含的统计思想.
方差作为刻画数据离中趋势的统计量,它全面、平均地反映一组数据与其平均数的偏离程度,是现代统计学中最常用的统计量之一. 《课标(2011年版)》要求“体会刻画数据离散程度的意义,会计算简单数据的方差,知道可以通过样本方差推断总体方差,能解释统计结果,根据结果做出简单的判断和预测,并能够进行交流”[1]. 本文以北师大版八年级数学下册第六章第4节“数据的离散程度”(第1课时)为例,创设有助于学生自主探究与合作交流的问题情境,构建统计实验活动,让学生在经历统计实验活动的过程中体会刻画数据离散程度的意义,提炼方差的计算公式,领悟方差蕴含的统计思想,积累数学活动经验,增强应用意识,培养数据分析观念.
创设情境,温故知新
案例1 某农科院计划为某地筛选出适应性好、综合性状优、产量潜力大且产量稳定的水稻新品种. 为了解“南粳3908”“南粳5055”“南粳9108”三种水稻新品种的相关情况,农科院各用10块自然条件相同的试验田进行比较试验,得到各试验田每公顷的产量(单位:t)如表1所示[2].
根据这些数据估计,你认为农科院应该选择哪一种水稻品种?
探究活动1:如何比较三种水稻的产量水平?
(1)你能结合表1的数据直接估计出三种水稻每公顷的平均产量吗?请你先估计,再计算三种水稻每公顷的平均产量,并与你的估计进行比较(结果保留3位小数).
(2)根据三种水稻每公顷的平均产量,你认为农科院应该选择哪一种水稻品种?为什么?
(3)除了比较三种水稻每公顷的平均产量外,还可以从哪些方面对三种水稻每公顷的产量水平进行比较?
(4)表1中南粳3908每公顷的产量最大值是多少?最小值又是多少?它们相差多少?南粳5055和南粳9108呢?
(5)一组数据的极差有什么特点,它能反映这组数据的整体离散情况吗?是否还有其他的数学量可以刻画数据的波动情况呢?
设计意图 案例1力图让学生经历解决一个统计问题的全过程,激活学生用数据说话的意识,让其通过数据分析做出判断,解决实际问题,体会数据中蕴含的信息. 探究活动1意在引导学生从数据集中趋势的角度分析数据. 问题(1)旨在让学生直观估计三种水稻的平均产量,然后通过具体计算评判自己的估计水平,调整自己的估计;问题(2)(3)意在让学生发现南粳3908与南粳5055的平均产量最高,且相同,仅靠比较二者的平均产量还无法做出判断,让学生意识到仅考查数据的集中趋势是不够的,还需要从数据离散程度的角度进行考查,从而借助问题(4)引入刻画离散程度的一个量——极差;问题(5)旨在让学生明确极差是一组数据中最大值与最小值的差值,它可以描述一组数据的波动范围,但它仅反映了这组数据中两个极端值的离散程度,没有充分利用整组数据信息,不能反映这批数据离散的整体情况,还需寻找其他的数学量精确刻画数据的整体离散程度.
建构活动,领悟意义
探究活动2:考查一组数据的离散程度需要有一个比较标准,用什么量作为比较标准比较合适?如何与这个标准进行比较呢?[3]请你思考如下问题.
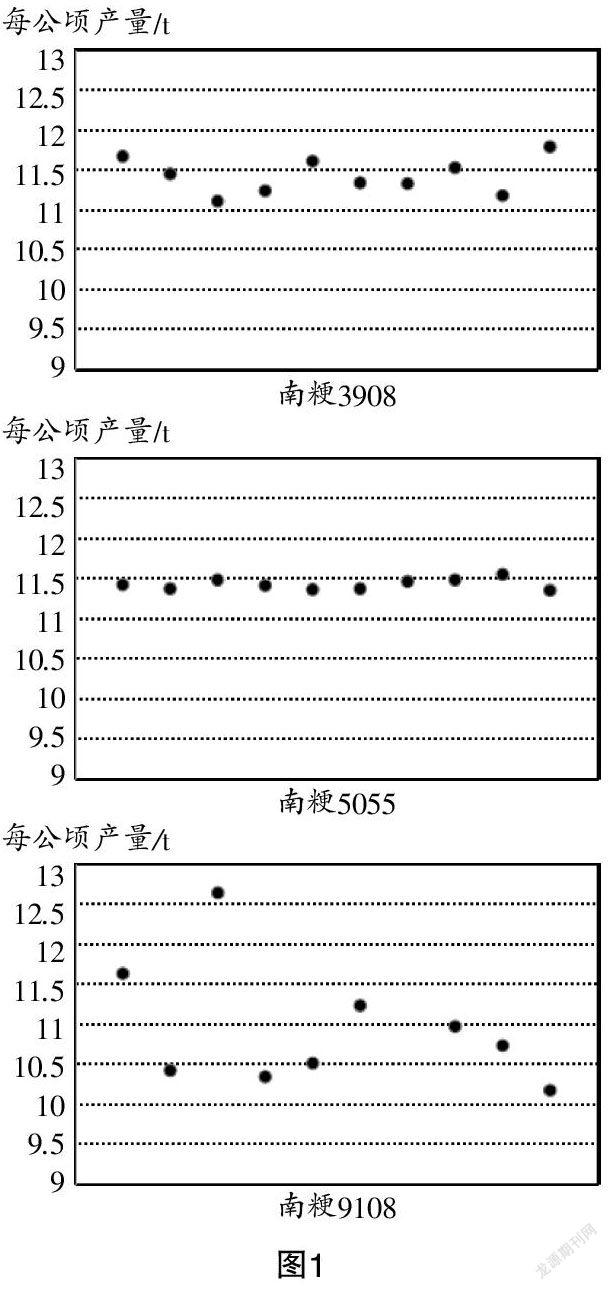
(1)把表1的数据表示成如图1所示的散点图. 观察图1,三种水稻每公顷的产量分布有什么特点?
(2)在图1中画出纵坐标等于平均数的直线,观察数据的分布与其平均数所在的直线之间的位置关系,你有什么发现?
(3)如何量化单个数据相对其平均数的偏离程度?又如何量化整组数据相对其平均数的偏离程度?
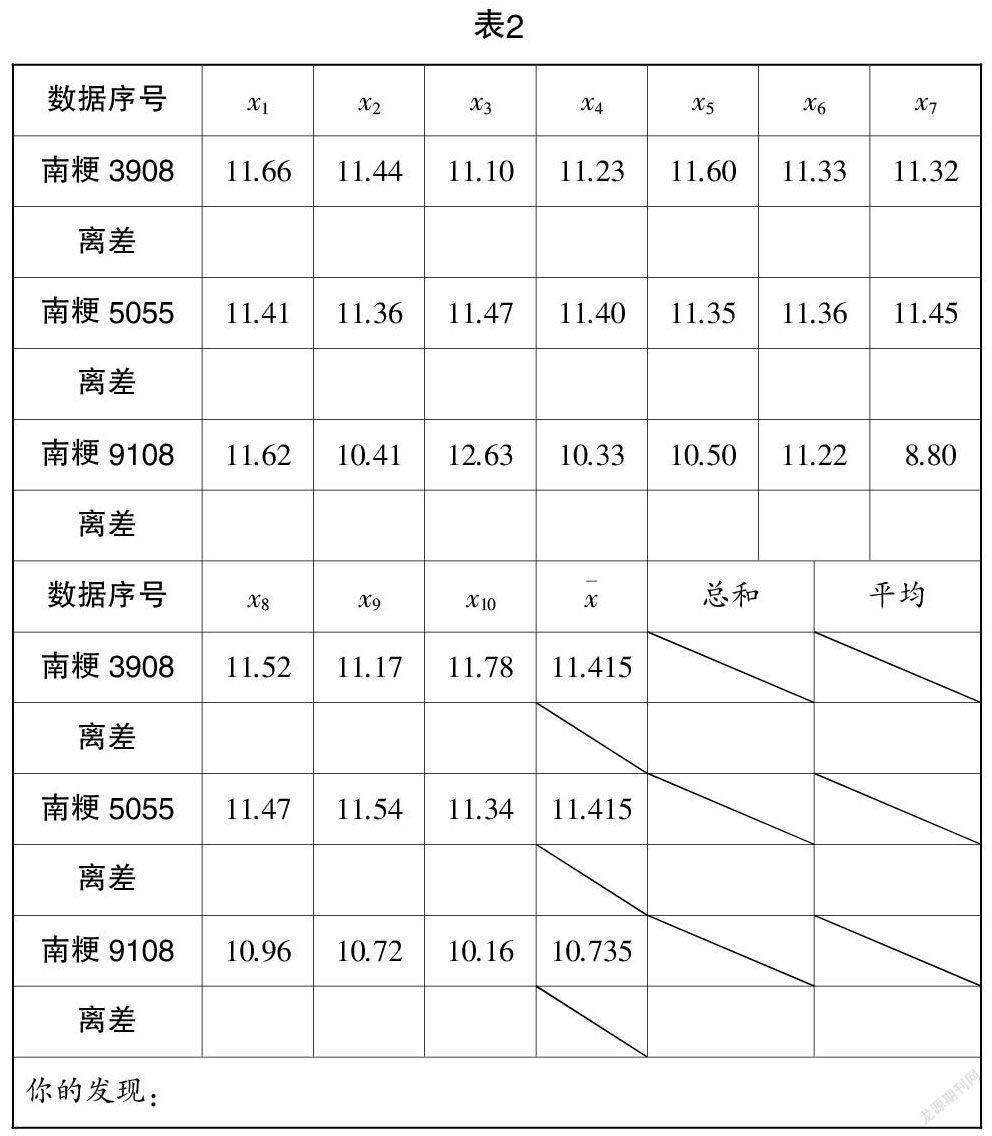
实验活动1:发放表2,指导学生利用Excel软件或者计算器,合作完成表2的探究内容(结果保留3位小数).
(4)如何对“离差”进行数学处理以避免出现正负相消的情况?你有哪些方案?
实验活动2:发放表3和表4,指导学生利用Excel软件或者计算器,合作完成表3和表4的探究内容(结果保留3位小数).
设计意图 探究活动2意在让学生经历利用“平均差”和方差刻画数据离散程度的过程,让學生意识到要刻画数据的离散程度首先要找到一个可以进行比较的参照对象. 为此,设置问题(1)让学生直观分析数据的离散程度,再通过问题(2)引导学生发现三种水稻每公顷的产量均集中分布在各自的平均产量附近,且围绕其平均产量上下波动. 从而让学生意识到,刻画数据的离散程度的比照对象就是这批数据最集中的位置,即反映数据集中趋势的平均数;问题(3)意在引导学生发现并采用“离差”(数据与其平均数的差)来量化单个数据相对其平均数的偏离程度,通过将这些“离差”求和或求平均数的方式来量化整组数据相对其平均数的偏离程度. 然而通过实验活动1,学生自然会发现,这些“离差”的总和为0,从而导致这批数据的离散程度由于这批“离差”中的正负抵消而不能真正刻画数据的离散程度. 为此,通过问题(4)继续引发学生思考,让学生在讨论与交流中得出两种常见的数学处理方式——对“离差”作绝对值或平方. 通过实验活动2完成三种水稻每公顷的产量的离散程度的量化,为后续生成“平均差”和方差(标准差)的概念做好铺垫.
模型归纳,生成概念
1. 模型归纳,酝酿概念?摇
师生共同回顾刻画数据离散程度的过程(见图2),总结计算“平均差”和方差的基本步骤[4].
2. 语言转化,生成概念?摇
3. 对比分析,了解优劣
问题:通过实验活动2,我们分别计算出三种水稻每公顷产量的“平均差”和方差(表5),如果利用“平均差”和方差分析三种水稻每公顷产量的波动状况,你能得出什么结论?
探究活动3:观察南粳9108每公顷产量的“平均差”和方差的计算演示过程,你能结合加权平均数的知识进行分析吗?谈谈你的发现.
4. 概念延伸,回归精确
问题:通过探究活动3,我们发现在实际应用中,用方差来描述数据的离散程度时,由于计算中进行了平方,从而可能放大该组数据离散的程度,并且其单位与原来数据的单位不一致,你能继续改进这个量吗?
设计意图 首先通过模型归纳,由特殊到一般,引导学生归纳小结求一组数据的平均差和方差的一般步骤与计算公式. 通过对比分析,引导学生发现,“平均差”或方差越大,数据的波动越大;“平均差”或方差越小,数据的波动越小. 通过探究活动3继续引导学生发现,“平均差”是离差的简单算术平均数,离差的大小并不影響其权重,所以对于“平均差”来说,极端数据的变异性被同等看待了. 而方差则可以看成是以离差本身大小为权重的加权平均数,所以越极端的数据会被给予越多的关注,这一点也更符合人们对于数据变异性的直接感[5],因此,采用方差就比较有效地衡量出这种变异性. 最后通过概念延伸,引出标准差s的概念,即s=. 让学生明确标准差既能从量上反映这批数据的离散程度,又能使单位与实际相一致,同时也避免方差由于平方后可能夸大离散的程度.
案例研习,运用概念
1. 典例示范,提升学力
案例2 2019年10月1日上午10时,北京天安门广场隆重举行庆祝中华人民共和国成立70周年阅兵式活动. 宽阔的长安街上,大军列阵,铁甲生辉. 巍峨的天安门前,旌旗飘扬,举世瞩目. 这是中国特色社会主义进入新时代的首次国庆阅兵,也是共和国武装力量改革重塑后的首次整体亮相. 古老沧桑的中华民族,久经风雨的伟大祖国,在这场举世关注的阅兵盛典中焕发出胜利与自豪的荣光(播放国庆70周年阅兵分列式视频片段,约2分钟).
我们知道接受检阅的仪仗队必须精挑细选,整齐划一,特别注重队员的身高,表6是从甲、乙两支仪仗队队员中随机选取的10名队员的身高(单位:cm),哪支仪仗队队员的身高更为整齐?你是怎么判断的?
探究活动4:当样本数据较大时,方差的计算较为繁复,你有什么方法可以简化计算吗?
(1)如果以185(cm)为基准,将甲、乙两组数据都减去185后再计算两组新数据的方差会有什么结果?你有什么发现?
实验活动3:发放表7,让学生利用Excel软件或者计算器,合作完成表7的探究内容(结果保留2位小数).
(2)你能利用完全平方公式和离差的性质(数据离差的代数和为0),化简方差的计算公式吗?
2. 公式应用,内化新知
案例3 某单位要买一批直径为60 mm的螺丝.现有甲、乙两个螺丝加工厂,它们生产的螺丝的材料相同,价格也相同. 该单位分别从甲、乙两厂的产品中抽样调查了20个螺丝,它们的直径(单位:mm)如下:
甲厂:60,59,59.8,59.7,60.2,60.3,61,60,60,60.5,59.5, 60.3,60.1,60.2,60,59.9,59.7,59.8,60,60;
乙厂:60.1,60,60,60.2,59.9,60.1,59.7,59.9,60,60,60, 60.1,60.5,60.4,60,59.6,59.5,59.9,60.1,60.
你认为该单位应买哪个厂的螺丝?[6]
设计意图 案例2旨在让学生重温国庆70周年阅兵分列式的震撼场面,切身感受到祖国的强大和繁荣,增强学生的民族自豪感,培养爱国主义情怀. 构建探究活动4引发学生深入思考,通过简化方差的计算公式,引导学生经历处理数学问题的过程,提升学生形式化的推理能力,激发学生学习统计和数学的兴趣. 案例3则意在让学生进一步熟练应用平均数、方差(标准差)解决实际问题,体会二者的统计意义,明确在实际应用中,对不同组别的数据进行比较选择时,当各组数据的差异较大时,应当首先考虑平均数的作用;当各组数据的平均数相等或者很接近时,要结合数据的离散程度进行分析,根据离散程度来进行选择.
梳理小结,归纳提升
问题:(1)本节课你学习了哪些知识?你能刻画“成绩更稳定”这种直观判断吗?
(2)极差、平均差和方差(标准差)有什么作用?
(3)怎样合理利用方差(标准差)解决实际生活中的问题?
设计意图 引导学生回顾极差、平均差和方差(标准差)等相关知识的产生和获得过程,构建知识结构框图(图3)[7],培养学生归纳和总结知识的能力,重点在回顾方差的概念生成过程和理解方差(标准差)的统计意义上.
结束语
本文通过创设有助于学生自主探究与合作交流的问题情境,构建有效的统计实验活动,使学生经历完整的统计过程,包括收集数据、整理数据、展示数据、从数据中提取信息,并利用这些信息说明问题. 本文旨在让学生在这样的过程中,不断积累统计经验,加深理解统计思想与方法,使统计学的教学散发出它原本应有的活力与乐趣,增强中学生对统计学的学习兴趣与能力.
参考文献:
[1] 中华人民共和国教育部.义务教育数学课程标准(2011年版)[S].北京:北京师范大学出版社,2012.
[2] 张鹏,王中德,周宝红,步学林,王君,温凯. 水稻品种比较试验[J]. 现代农业科技,2020(21).
[3] 万荣庆. 清晰认识概念 理解数学本质——对“方差”概念的分析与思考[J]. 复印报刊资料:中学数学教与学, 2009(06).
[4] 王华. 关注概念形成 激活学生思维——“方差与标准差”概念形成过程的两次教学设计[J].中国数学教育,2014(05).
[5] 梅林晨. 对于平均差与标准差的数学关系和应用价值比较研究[J]. 赤峰学院学报(自然科学版),2015,31(15).
[6] 马复. 义务教育教科书·数学(八年级上册)[M].北京:北京师范大学出版社,2012.
[7] 封小波. 构建统计实验活动 树立数据分析观念——以“平均数”教学为例[J]. 中学数学教学参考,2020(29).

