基于风电机组无功裕度预测的风电场无功分层控制策略
刘颖明,刘闯闯,王晓东
(沈阳工业大学 电气工程学院,辽宁 沈阳 110870)
0 引言
大规模风电场并网会造成电网电压波动,通过控制双馈式风电机组(Doubly-Fed Induction Generator,DFIG)及静止无功发生器(Static Var Generator,SVG)可以维持并网点 (Point of Common Coupling,PCC)的电压稳定,明显改善电压波动[1]。文献[2]为解决并网风电场无功电压调节易受风功率波动影响的问题,提出了基于分层模型预测控制的电压协调控制策略,有效抑制了PCC电压波动,但未考虑机组有功输出与无功输出的内在联系。文献[3]推导出DFIG无功输出极限关系式,然而当DFIG以其自身无功极限进行无功补偿时,将有可能因输出功率越限而脱网,从而导致电网电压波动。文献[4]为风电机组预留出无功裕度,分析了风电场无功裕度与其当前无功功率的关系,通过协调控制避免了无功越限的发生。文献[5]提出等裕度无功分配策略,有效防止了变流器电流越限发生跳机的现象,但未考虑无功调节过程中调节指令的低时效性问题。在预测算法方面,文献[6]提出了一种小波变换、支持向量机和粒子群的混合模型,但与传统交叉验证法相比,精度并没有提升太高。文献[7]提出了基于改进的经验小波变换和最小二乘支持向量机的混合预测模型,并通过鸟群算法对参数进行联合优化,提高了预测性能。上述研究对双馈式风电机组无功调节能力和风电场无功裕度的计算与应用进行了有益探索,但在利用风电机组无功调节能力进行电网电压调节时,都未将无功控制指令的时效性、风电功率的预测与实时校正、风电机组出口电压的波动性考虑在内。
本文以双馈式风电机组为研究对象,采用混合预测算法进行风电功率预测,同时提出了一种预测功率的实时校正方法,并由校正后的有功功率预测值计算风电机组的无功裕度预测信息,进而提出基于风电机组无功裕度预测的风电场无功分层控制策略。在风电场层面,无功分层控制以并网点电压偏差和线路有功损耗最小为目标,求解风电场无功参考值;在风电机组层面,以风电机组的出口电压波动最小和预测无功裕度最大为无功分配依据,向场内DFIG和SVG下发无功任务,从而改善电网和机组出口电压并为风电场预留出充足的无功裕度。最后以实际算例仿真验证所提控制策略的可行性。
1 风电场无功分层控制模型
本文提出的无功控制策略分三层实现,即风电场的电压求解层、无功整定层和无功分配层,其控制原理框架如图1所示。

图1 风电场无功分层控制原理Fig.1 Reactive power layered control principle of wind farm
各层和功能模块在滚动周期和指令执行周期的时间分辨率如表1所示[8]。其中,风电功率预测模块超短期风电预测为15 min预测,1 min采集一次机组实时输出有功功率,在滚动周期内共执行15次预测校正。

表1 时间分辨率Table 1 Time resolution table
2 风电场无功分层控制策略
2.1 最优并网电压求解
①并网电压偏差最小
风电场并网点处的电压须要满足电网要求,具有良好的跟踪特性[9],因此选择并网点电压Upcc与参考电压差最小目标为
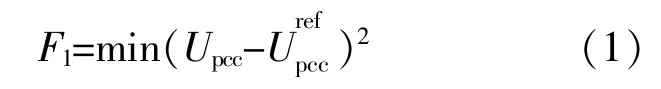
②线路有功损耗最小
风电场内风电机组的线路有功损耗最小时有 [9]:
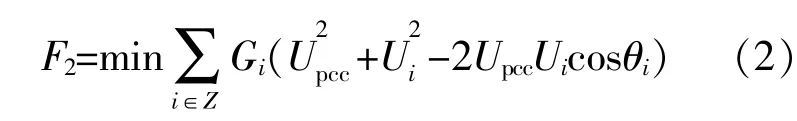
式中:Z为与PCC相邻的节点数;Gi为PCC与节点i之间线路的电导;Ui为节点i处的电压幅值;θi为PCC与节点i之间实测的电压相角差。
③PCC潮流约束方程

为了防止风电场脱网运行,节点电压须要维持在额定值-3%~7%,即:

④目标函数
并网点电压偏差和线路有功损耗最小的多目标,通 过 权 重 系 数 λ(0<λ<1)可 转 换 为 单 目 标 优化,λ要综合考虑并网点电压偏差和线路有功损耗两个子目标对总目标函数的贡献权重。综上,目标函数为
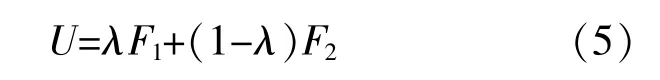
⑤模型求解
本文的优化模型能够表述为标准二次规划(Quadratic Programming,QP)问题,采用Matlab进行实时在线优化求解,得到满足约束条件的实时最优并网点电压,并以此作为计算风电场无功参考值的电压参考信号[10],[11]。QP的系数矩阵H和f分别为
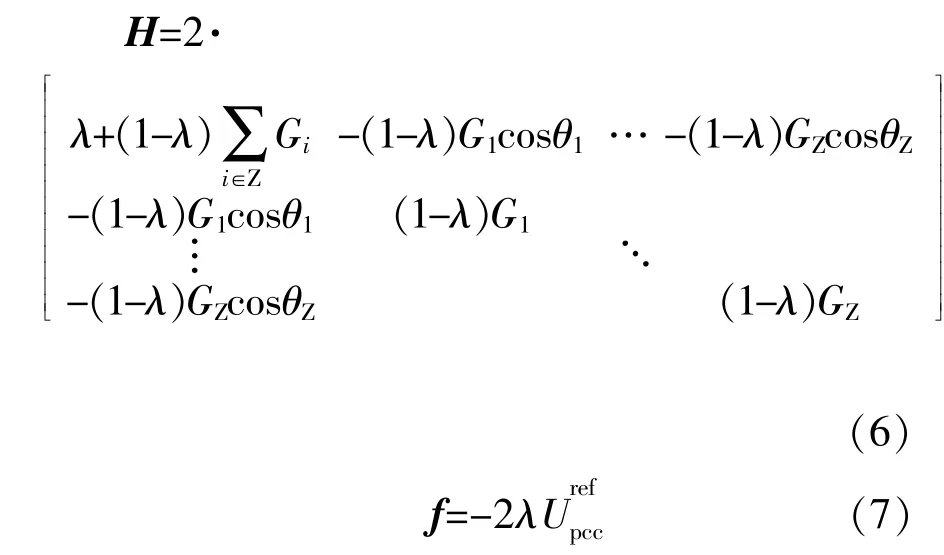
2.2 风电场无功参考值求解
比例积分(Proportion Integration,PI)控制器可以消除电压的稳态误差[12]。将并网最优电压与PCC当前电压做差,求得偏差电压ΔU,通过PI控制器得到风电场无功参考值,具体过程如图2所示。
图中:Tr为电压测量滞后时间常数,用于模拟采样延时;Tc为与各个DFIG的通信延迟等相关的时间常数用于模拟输出延时;KP和KI分别为PI环节中的比例积分系数;Qmax和Qmin分别为风电场输出无功的上、下限,当输出越限时以限值为输出量。
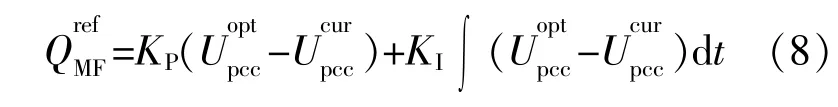
式中:KP≈U/X,X为并网点与风电机组汇集母线之间输电线路的电抗[12];KI依据经验整定。
2.3 基于无功裕度预测的无功优化分配
2.3.1基于EWT-LSSVM的风电功率预测
风电功率预测可以有效消除风电功率波动带来的影响,提高风电并网可靠性。本文采用文献[7]所提方法进行风电功率预测。首先将原始信号通过经验小波变换(Wavelet Transform,EWT)分解,得到更具规律性和平稳性的分量,该分量作为最小二乘支持向量机(Least Square Support Vector Machine,LSSVM)的输入,LSSVM对各分量分别进行预测以提高预测精度,最后将各分量预测结果进行重构得到预测值。预测过程如图3所示。
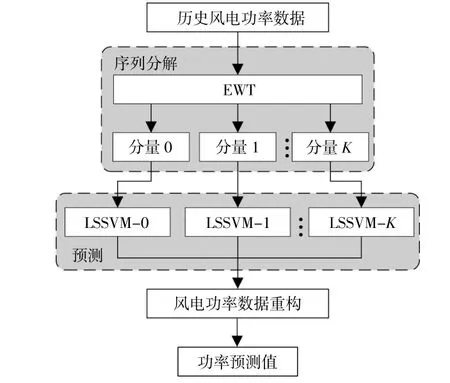
图3 风电功率预测框图Fig.3 Wind power prediction block diagram
选取历史风电功率数据作为原始信号f(t),EWT方 法 将f(t)分 解 为K个 固 有 模 态 分 量[7],其中各模态分量为

得到的模态分量作为LSSVM的训练样本数据(xi,yi),i=1,2,…,L,L为 训 练 样 本 长 度。LSSVM将传统支持向量机中二次规划问题转化为线性方程 组 求 解[7],简 化 了 求 解 的 过 程,对 于(xi,yi)满 足线性方程组:
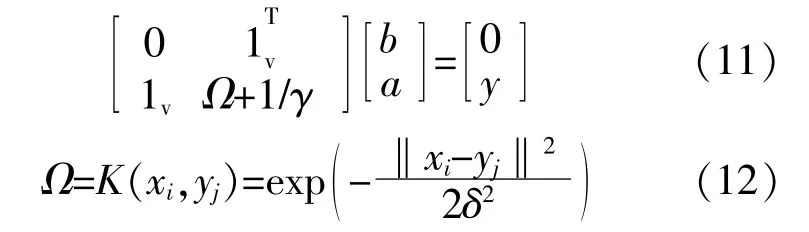
式 中:1v=[1,1,…,1]T;γ为 正 则 化 参 数;b为 偏 差项;a为 拉 格 朗 日 乘 子,a=[a1,a2,…,aL]T;y为 样 本输 出 值,y=[y1,y2,…,yL]T;Ω为 核 函 数,本 文 取 为 径向基核函数;δ为核函数的带宽。

对于新的样本x,训练后的LSSVM模型输出为式 中:ai,b由 式(11)和(12)求 解 得 出。
最后将各分量预测结果进行叠加,得到最终的风电功率预测信息。
2.3.2预测功率校正
预测功率校正能够使预测更接近实际风电。校正功率、超短期预测功率与实际功率之间的误差e1,e2分 别 为

此外,为保证功率输出快速逼近实际功率,取实时校正功率为

考虑功率校正后的预测功率为

式中:T为超短期风电功率预测周期时长,T=15 min;Δt为校正周期时长;m为校正次数,本文m=15。
2.3.3无功优化分配目标函数
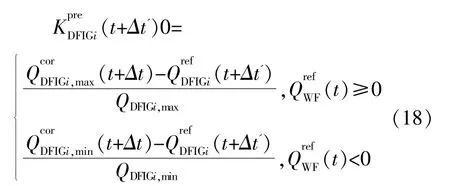
式中:Δt′为DFIG无功控制周期时长,本文Δt′=Δt/12;Q(t+Δt′)为Δt′时刻后机组待发无功功率的参 考 值 ;QDFIGi,max和QDFIGi,min分 别 为 机 组 的 最 大 和最小无功极限。
由AVC实时测得各DFIG的无功功率和电压 分 别 为QDFIGi(t)和UDFIGi(t),上 一 无 功 控 制 周 期的 无 功 功 率 和 电 压 分 别 为QDFIGi(t-Δt′)和UDFIGi(t-Δt′),则 第i台DFIG无 功 电 压 灵 敏 度 为
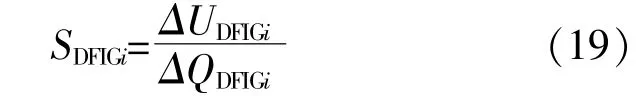
由于Δt′很小,可认为在Δt′时间内无功电压灵 敏 度 变 化 不 大,SDFIGi(t+Δt′)≈SDFIGi(t),即:

由 式(20)可 得t+Δt′内 电 压 波 动 为

以t+Δt′时刻风电机组的出口电压波动最小和预测无功裕度最大为无功分配原则,通过引入权 重 系 数γ(0<γ<1)并 对 第 二 个 子 目 标 取 负 值,将多目标求解问题转换为单目标最小值优化问题。为了便于使用二次规划求解,取目标函数为

2.3.4约束条件
各DFIG在t+Δt′时刻输出的无功功率应小于预测无功极限,即:

当DFIG能够满足风电场无功需求时,优先考虑DFIG输出,此时DFIG所发无功应满足:

当DFIG无功无法满足风电场无功需求时,以预测无功极限值输出:
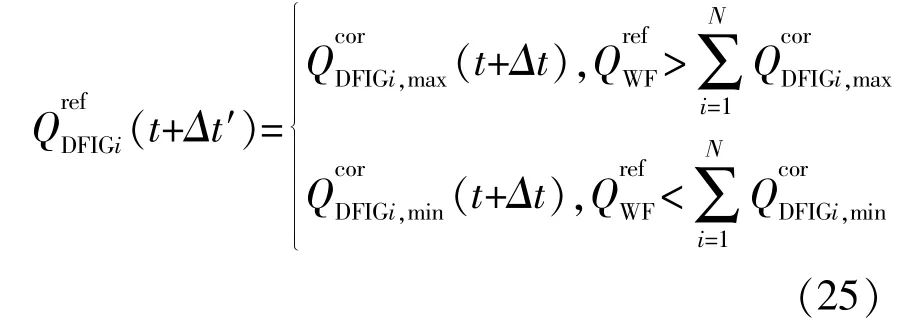
剩余无功由SVG承担,即:
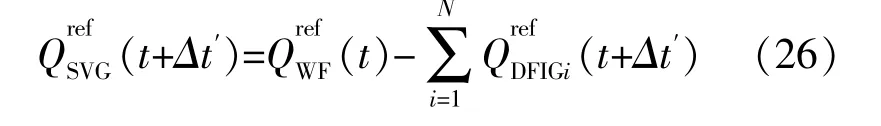
3 算例分析
为验证所提方法的有效性,本文以辽宁108 MW双馈风电场为例,其拓扑如图4所示。

图4 算例仿真模型Fig.4 Case simulation model
风电场由3台36 MW等值风电机组(WT)和12 MVar SVG组成,其中36 MW等值风电机组由24台参数相同的1.5 MW双馈式风电机组组成。风电场通过35 kV/220 kV变压器并入到电网。本文不考虑地形和叶片尾流对风速的影响,设定每台等值风电机组在不同风速下运行。在QP求解中,权重系数选取综合考虑子目标对总目标函数的 贡 献,本 文λ=1-1/∑Gi≈0.9,γ=0.8。
3.1 校正后风电功率预测效果分析
等值风电机组WT3的预测效果如图5所示。
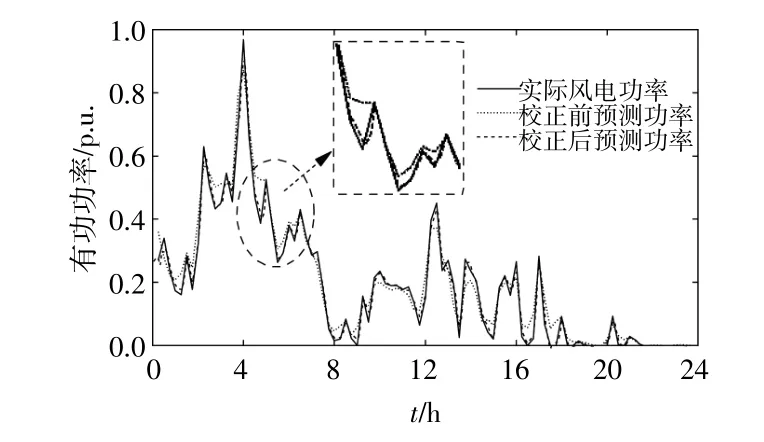
图5 WT3的实际、预测与校正后风电功率对比Fig.5 Comparison of actual,predicted and corrected wind power of WT 3
由图5可知,校正后的风电功率预测曲线与实际功率曲线更加接近,预测效果更好。
功率预测曲线的归一化均方根误差(Normalized Root Mean Square Error,NRMSE)和 归 一 化平均绝对误差(Normalized Mean Absolute Error,NMAE)评估结果如表2所示。

表2 预测精度比较Table 2 Comparison of forecasting accuracy
由表2可知,所提预测功率校正方法取得了良好的预测效果,可以应用于风电机组无功裕度预测信息的实时求解过程。
3.2 策略控制效果分析
为分析不同控制方式对风电机组出口电压和无功裕度的影响,并验证所提出的优化控制策略,本文采用以下两种控制方式进行仿真对比。①传统比例控制策略 (Traditional Proportional Control Strategy,TPCS),以并网点电压偏差和线路有功网损最小为目标,不考虑风电功率预测信息,按各DFIG和SVG的无功容量对风电场内DFIG和SVG进行比例无功分配。②本文优化控制策略(Article Optimal Control Strategy,AOCS),利 用 本文提出的基于无功裕度预测的无功分层控制策略进行风电场无功任务的优化分配。
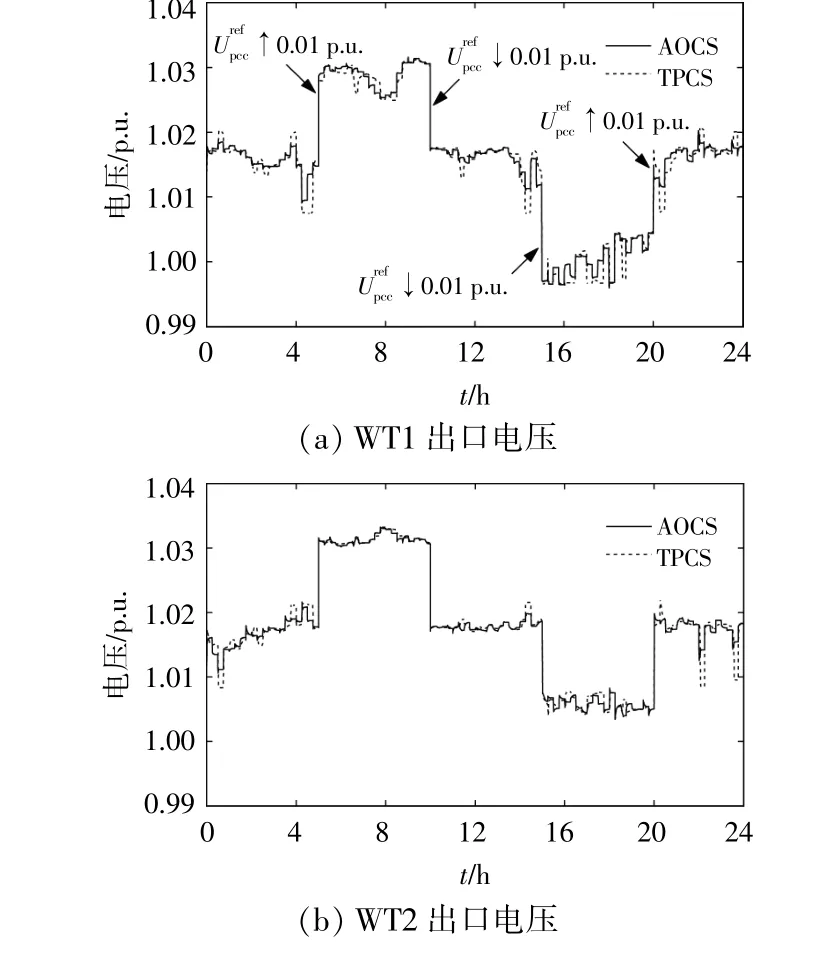

图6 不同控制策略下WT的出口电压对比Fig.6 Comparison of wind turbine outlet voltage under different control strategies
为了验证WT出口电压稳定性,取标准差(σ)指标进行评估,评估结果如表3所示。
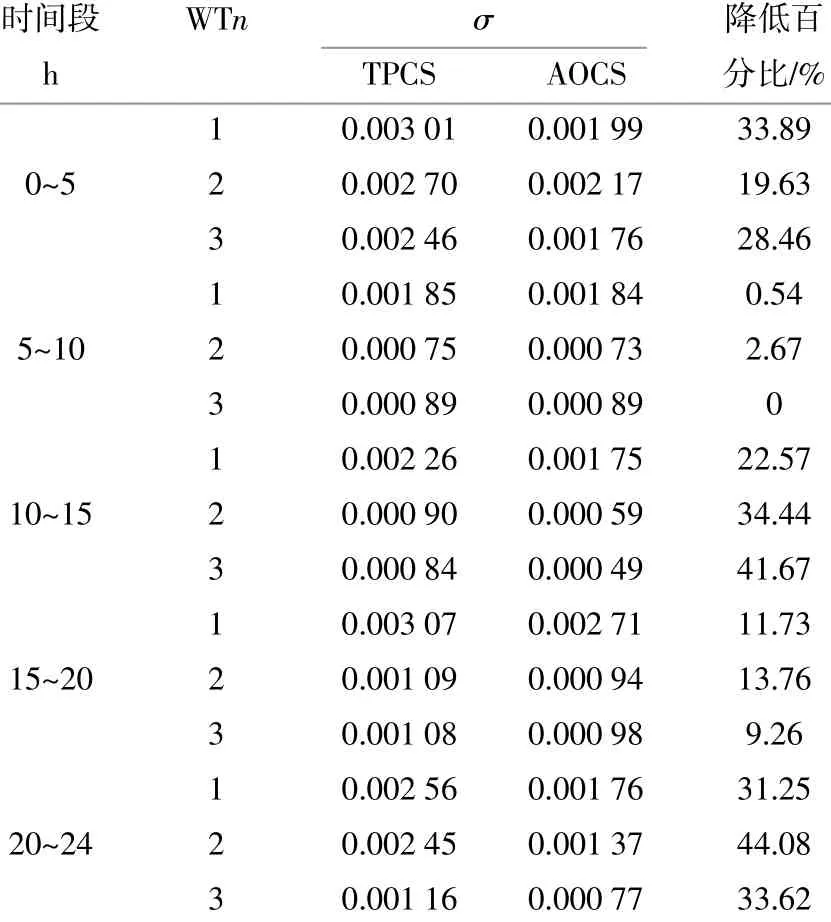
表3 1 d内不同控制策略下的电压波动性评估结果Table 3 Evaluation results of voltage fluctuation under different control strategies in one day
由图6和表3可知,传统控制策略由于未能预知未来功率波动而提前做出规划调整,电压波动较大。本文所提策略在无功控制过程中将实时校正的预测风电功率,根据每台风电机组未来时段内的功率波动信息合理规划分配无功指令,实现控制周期内无功的协调优化,降低了风电机组出口电压的波动性。对于1 d内风电场整体的控制效果而言,采用基于功率预测的优化控制策略具有较小的标准差,风电机组出口电压波动性较小、稳定性更高,电压波动的标准差最大减小44.08%,平均减小21.76%。
3.3 风电机组无功出力分析
根据本文所提的无功裕度计算方法,得到风电机组预测无功极限与实际输出无功功率对比,如图7所示。

图7 风电机组输出无功功率极限与实际输出对比Fig.7 Reserved reactive power margin under different control strategies in a day
由图7可知,采用本文优化控制策略进行机组无功分配,各机组根据相应的预测无功极限进行无功出力,在无功调节过程中,高无功发生能力的风电机组承担相对较多的无功任务,充分发挥了DFIG的无功调控能力。
计算1 d内AOCS和TPCS策略控制下各WT的预留无功裕度,结果如表4所示。

表4 1 d内不同控制策略下的预留无功裕度Table 4 Reserved reactive power margin under different control strategies in a day
由图4可知,本文所提控制策略预留出了相对多些的无功裕度,其中WT3比传统控制多出1.12%,说明依据预测无功极限协调机组无功出力可以在一定程度上增加风电场的无功裕度。
4 结论
针对风电场无功控制时效性低的特点,本文提出了一种基于风电机组无功裕度预测的风电场无功分层控制策略。该策略预测误差在NRMSE评估指标中由平均4.99%降低到2.11%,在NMAE评估指标中由平均3.72%降低到1.61%,提高了预测的精度。本文提出的分层协调控制策略,分别实现了对风电场和风电机组两个层面的优化处理,通过引入校正后的功率预测信息,提高了无功控制指令的时效性,有效地协调了各机组无功出力,在为各风电机组预留出相应无功裕度的同时,降低了风电机组出口电压波动性,电压波动的标准差最大减小44.08%,平均减小21.76%。

