新型忆阻光伏电池的建模与分析

董 军，石 杰，高明煜，孙平远

（1.杭州师范大学 材料与化学化工学院，浙江 杭州 311121；2.杭州电子科技大学 电子信息学院，浙江杭州 310018；3.浙江大学 电气工程学院，浙江 杭州 310027）

0 前言

近年来，为解决能源危机、环境污染和经济发展等问题，新能源发电系统及相关技术快速发展。光伏发电系统因其清洁、环保、储量丰富等优点在新能源发电系统中脱颖而出[1]，[2]。光伏电池是光伏发电系统的关键设备，光伏电池的建模与仿真对光伏发电系统的综合性研究非常重要。目前，光伏电池的仿真模型主要分为两类，分别为基于等效电路法的物理模型和基于函数拟合法的行为模型[3]～[8]。其中：基于等效电路法的物理模型易受环境温度和太阳辐射强度的影响，因此，其输出特性具有明显的时变特征；基于函数拟合法的行为模型在构建过程中须要大量的实时数据作为支撑，当外部环境发生变化时，基于函数拟合法的行为模型须要不断地调整拟合函数中可变参数的取值，以保证拟合精度满足要求。综上可知，与基于等效电路法的物理模型相比，基于函数拟合法的行为模型能够更好地描述光伏电池的输出特性。但是，基于函数拟合法的行为模型并不适用于实际的应用研究[9]。因此，建立一种既贴近光伏电池的物理特性，又能对光伏电池动态过程进行自适应描述的建模方法，是一项具有挑战的工作。

1971年，Chua L基于电路理论公理化体系的完备性阐述定义了忆阻器的概念[10]。2008年，Tour J M发明了忆阻器[11]。学者们通过实验发现，忆阻器具有独特的开关转换机制、自动的记忆功能、连续的输入输出特性，这些特性使得忆阻器在非易失性存储器、人工神经网络、大规模集成电路等 方 面 有 着 巨 大 的 应 用 潜 力[12]～[15]。

本文基于光伏电池的物理模型和忆阻器的非线性特性，运用忆阻器分别替代光伏电池经典模型中的二极管和旁路电阻，构建了两类新型忆阻光伏电池模型；然后，通过严谨的数学推导对这两类模型的输出特性进行深入研究，并通过一系列的数值仿真验证了本文方案的有效性和科学性。由于忆阻器对参数的敏感性，使得忆阻光伏电池模型具备一定的时变特性，这一特性能够较好地解决传统光伏电池建模过程中存在的自适应性弱、无法完全展现光伏电池输出特性的问题。

1 忆阻光伏电池模型

光伏电池输出特性易受外界环境变化的影响。为了更加准确地描述外界环境（环境温度和太阳辐射强度）对光伏电池输出特性的影响，以及为光伏阵列拓扑结构和最大光伏功率点跟踪算法的设计提供理论基础和实验支撑，本文基于经典的光伏电池模型和忆阻理论，提出了两类新型忆阻光伏电池模型。

1.1 光伏电池模型

根据量子学理论[1]，光伏电池等效电路模型可以分为3种，分别为光伏电池的理想模型、简化模型和实际模型。光伏电池等效电路模型如图1所示。图中：IPV为光生电流 （与太阳辐射强度成正比），A；ID为 流 经 二 极 管 的 电 流，A；Rs为 理 想 模 型串联电阻（用于表示不可忽略的阻抗效应），Ω；Rp为简化模型的旁路电阻 （用于表示模拟光伏电池中漏电流导致的漏电阻等实际现象），Ω；I为流经光伏电池负载的电流，A；V为光伏电池两端的电压，V。

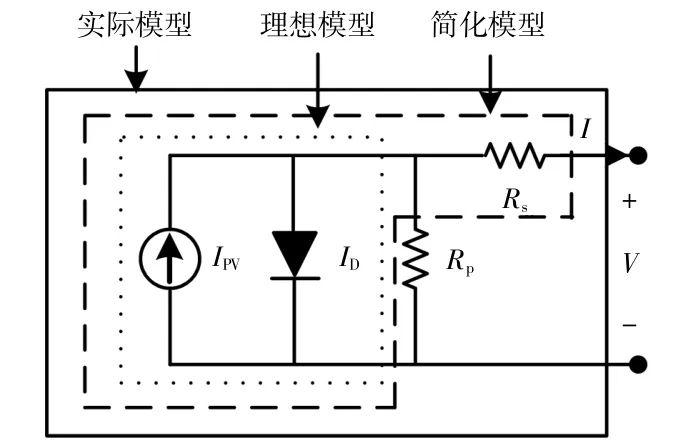
图1 光伏电池等效电路模型Fig.1 The equivalent circuit model of photovoltaic cell

由图1可知：理想模型为最简单的电路模型，其电压、电流表达式有利于清晰地展示光伏电池的基本特性；简化模型在理想模型的基础上增加了串联电阻Rs；实际模型在简化模型的基础上增加了旁路电阻Rp。根据基尔霍夫电流定律，光伏电池理想模型、简化模型和实际模型的伏安特性关系表达式分别为[1]

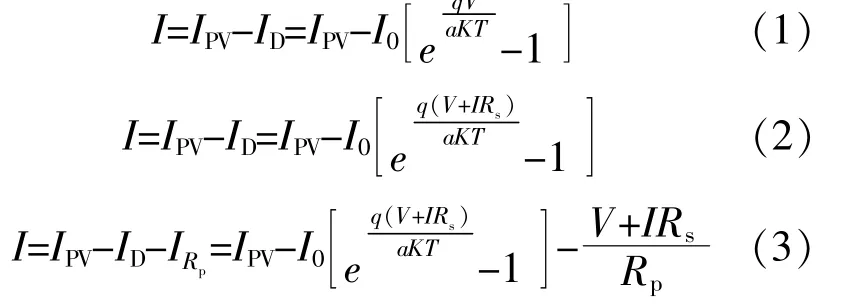
式中：I0为光伏电池反向饱和电流，A；q为电子电荷，取1.6×10-19C；K为 波 尔 兹 曼 常 数，取1.38×10-23J/K；T为绝对温度；a为P-N结的理想因子；IRp为流经旁路电阻Rp的电流，A。

1.2 忆阻光伏电池模型

1.2.1忆阻器

忆阻器作为一种具有记忆功能的无源非线性二端元件，其阻值能够根据供给电源的强度、极性以及持续供电时间发生连续性改变[15]。本节模型采用经典的惠普忆阻器模型，其阻值M（t）的计算式为[16]

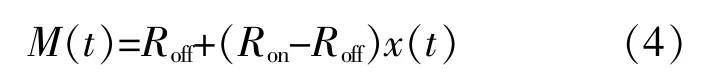
式 中：x（t）为 忆 阻 器 的 状 态 变 量；Ron，Roff分 别 为 忆阻器的极小忆阻值和极大忆阻值，Ω；t为时间，s。

x（t）的 计 算 式 为

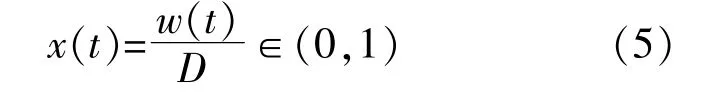
式 中：w（t）为 忆 阻 器 掺 杂 层 的 长 度，m；D为 忆 阻 器的总长度，约为10 nm。

当t=0时，令忆阻器初始阻值为M0。忆阻器的状态变量动态方程表达式为

式 中：μv为 平 均 离 子 迁 移 率，m2/（s·V）；η为 忆 阻器 极 性；i（t）为 流 经 忆 阻 器 的 电 流，A；f（x）为 窗 函数 [16]。

f（x）的表达式为

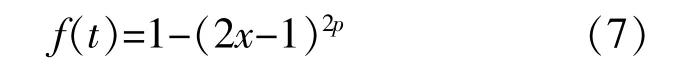
式中：p为窗函数的可控参数，p∈N+。

1.2.2忆阻光伏电池模型

本文提出的两类忆阻光伏电池模型运用了元件替换的方法。利用忆阻器分别替换光伏电池实际模型中的二极管和旁路电阻Rp。其中，利用忆阻器替换二极管后，得到I类忆阻光伏电池模型；利用忆阻器替换旁路电阻后，得到II类忆阻光伏电池模型。两类忆阻光伏电池的电路结构如图2所 示。图 中：I1，I2分 别 为I，II类 忆 阻 光 伏 电 池 模 型中流经串联电阻Rs的电流，A。

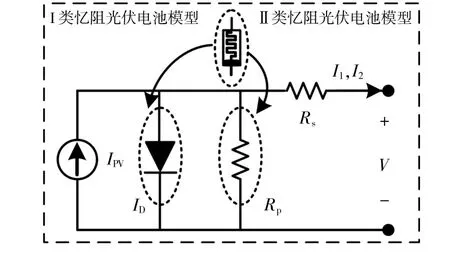
图2 忆阻光伏电池的电路结构Fig.2 The circuit configuration of memristive photovoltaic cell

基于式（3）得到I类忆阻光伏电池模型的伏安特性方程为

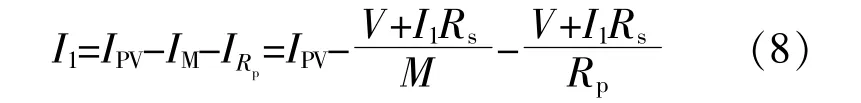
式中：IM为流经忆阻器的电流，A；M为忆阻器的阻 值，Ω。

同理，基于式（3）得到II类忆阻光伏电池模型的伏安特性方程为

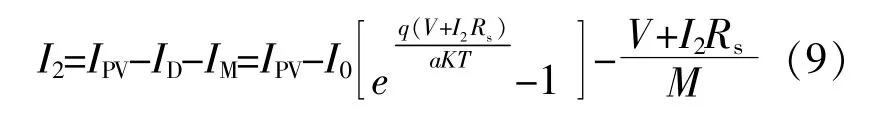
光伏电池等效电路模型中光生电流IPV以及反向饱和电流I0的计算式分别为[2]

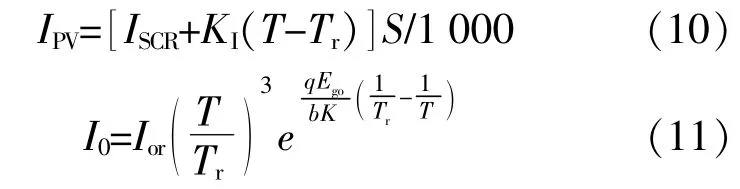
式中：ISCR为某一温度、太阳辐射强度下的短路电流，A；KI为短路电流温度系数；Tr为光伏电池参考 温 度，K；S为 太 阳 辐 射 强 度，W/m2；Ior为 参 考 温度下指定反向饱和电流，A；Ego为半导体材料跨越能带间隙时所需的能量，eV；b为曲线拟合系数。

1.3 模型实现及分析

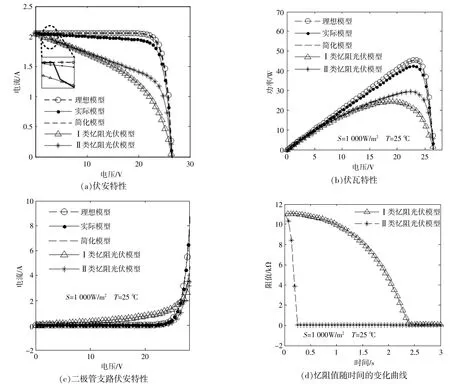
图3 不同光伏电池模型的仿真结果Fig.3 Experimental results of different photovoltaic cells

本文基于Matlab软件平台进行了一系列的对比仿真实验（定量分析实验），具体参数：极小忆阻值Ron=100Ω；极大忆阻值Roff=20 000Ω；忆阻器初始阻值M0=10 000Ω；平均离子迁移率 μv=10-14m2/（s·V）；短 路 电 流ISCR=2.52 A；光 伏 电 池 参 考 温度Tr=300 K；半导体材料跨越能带间隙时所需的能量Ego=1.35 eV；P-N结的理想因子a=1.6；曲线拟合系数b=1.6；短路电流温度系数KI=0.001 7 mA/K；参考温度下指定的反向饱和电流Ior=0.228 7×10-6A；串联电阻Rs=0.09Ω。其中，忆阻器的器件参 数（Ron，Roff，D，μv）主 要 取 决 于 忆 阻 器 的 制 作 工艺，且这些参数的设定值广泛应用于众多相关文献中[14]～[18]。其余光伏电池参数的提取主要通过拟合某一类真实光伏电池的V-I特性曲线得到。

图3中分别为通过仿真得到的5类光伏电池模型（理想模型、实际模型、简化模型、I，II类忆阻光伏电池模型）的伏安特性、伏瓦特性、二极管支路伏安特性，以及两类忆阻光伏电池模型的忆阻值随时间的变化曲线。

由 图3（a），（b）可 知，两 类 忆 阻 光 伏 电 池 模 型的伏安、伏瓦特性曲线的形态以及变化趋势与3类经典模型（理想模型、实际模型和简化模型）基本一致。由图3（a）可知，II类忆阻光伏电池模型的伏安特性曲线存在一个近似线性下降的区域[l4]，这是由该模型中忆阻器阻值的极速降低导致 的[图3（d）]。由 图3（c）可 知，当 非 线 性 忆 阻 元 件替代二极管（I类忆阻光伏电池模型）时，对应支路的伏安特性曲线与传统光伏电池模型相似，这说明忆阻元件可以替换非线性电路中的二极管。由图3（d）可知，相同忆阻器在电路中的位置不同时，会导致其所处的激励环境发生变化，从而导致忆阻器阻值的变化速率随之改变。

2 忆阻光伏电池模型参数分析

光伏电池模型的主要参数包括外界环境参数和内部器件参数两部分。外界环境参数主要包含环境温度T和太阳辐射强度S[1]～[3]；内部器件参数与电路模型的拓扑结构紧密相关。本文中5类光伏电池模型（理想模型、实际模型、简化模型、I，II类忆阻光伏电池模型）的外部参数均为环境温度T和太阳辐射强度S；对于内部参数，由于本文提出的两类忆阻光伏电池模型电路系统的多元化，内部参数的数量相比于经典的光伏电池模型有所增加，其中，I类忆阻光伏电池模型的内部参数包括光生电流IPV、反向饱和电流I0、串联电阻Rs、旁路电阻Rp、忆阻器总长度D、忆阻器横截面积SA、忆阻器初始阻值M0、忆阻器极性 η；II类忆阻光伏电池模型的内部参数在上述参数的基础上，增加了P-N结理想因子a、曲线拟合系数b、参考温度下的反向饱和电流Ior和跨越能带间隙时所需的能量Ego。由于忆阻器长度D和横截面积SA的偏差主要发生在忆阻器的制作工艺过程中，因此，可以将这两个参数统称为忆阻器的工艺参数。忆阻器长度D和忆阻器横截面积SA是由精密仪器测得的，测量完毕后，数值不会再发生改变；忆阻器初始阻值M0和忆阻器极性 η是由忆阻器的初始状态以及忆阻器在电路中的连接方式决定的。

2.1 外部参数对忆阻光伏电池的影响

本文假设太阳辐射强度和环境温度不会对忆阻器的特性产生影响。设定环境温度变化量为ΔT，太阳辐射强度变化量为 ΔS。基于式（10），（11）得到，外部参数改变后的实时光生电流和电池反向饱和电流的计算式分别为

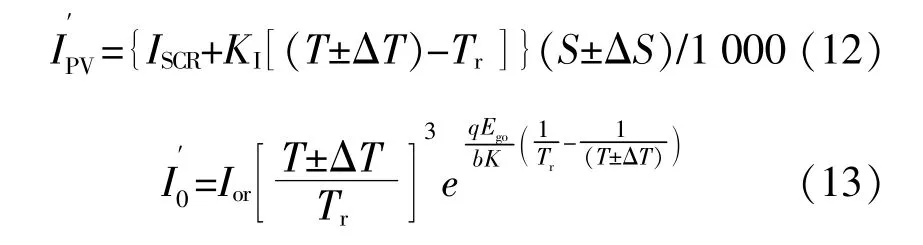
结 合 式（8），（9），保 持 太 阳 辐 射 强 度（或 环 境温度）不变，当环境温度（或太阳辐射强度）增大时，两类忆阻光伏电池模型中的实时光生电流均随之增大。忆阻光伏电池的反向饱和电流表达式较为复杂，基于该式难以判断电流的变化趋势。因此，本文通过Matlab数值仿真结果进一步讨论外部参数可能造成的影响，设定太阳辐射强度S集合 为{600，800，1 000，1 200 W/m2}，环 境 温 度T集合 为{15，30，45，60℃}。

本文采用控制变量法 （当研究太阳辐射强度对忆阻光伏电池模型的影响时，保持环境温度T为25℃；当研究环境温度对忆阻光伏电池模型的影响时，保持太阳辐射强度S为1 000 W/m2）研究外部参数对忆阻光伏电池模型的影响。研究结果如图4所示。

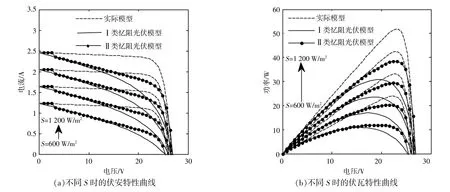
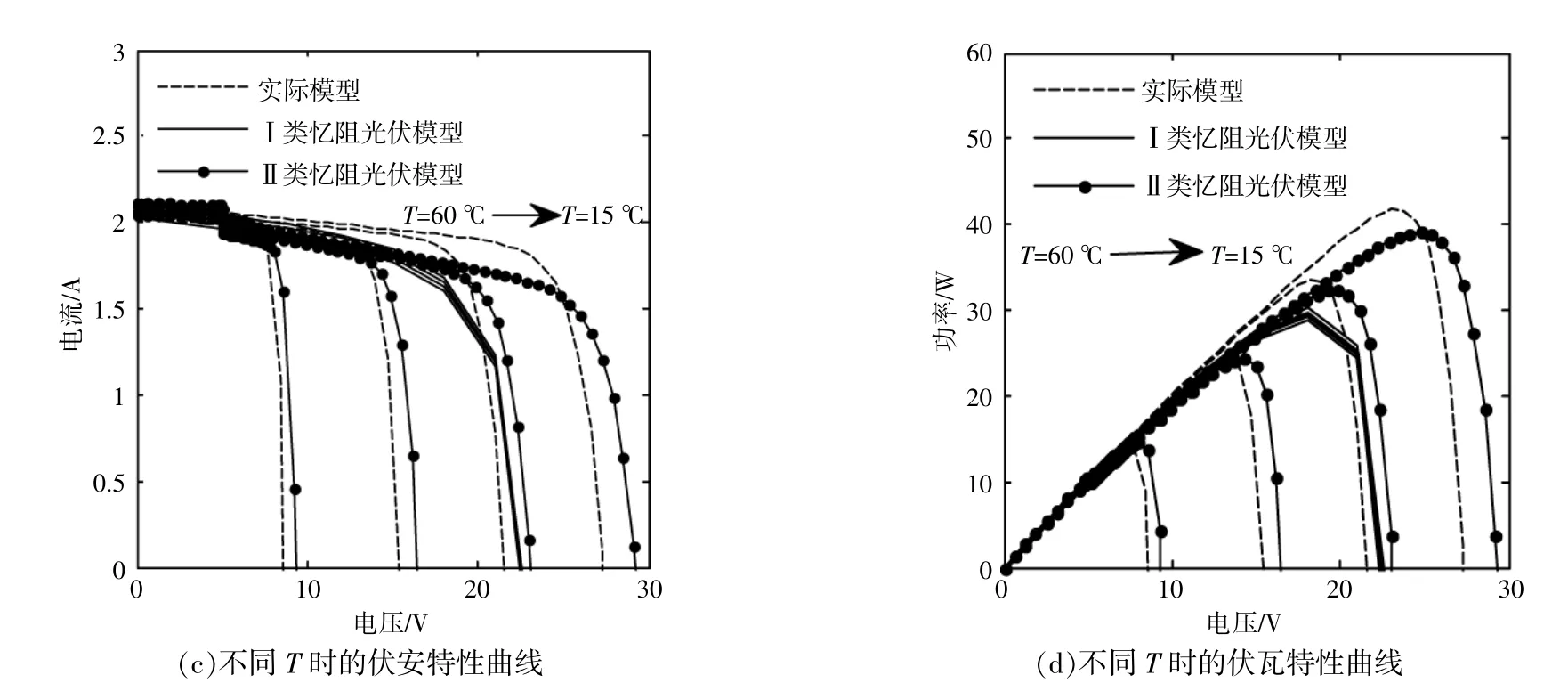
图4 外部参数对忆阻光伏电池模型的影响Fig.4 Effect of external parameters on memristive model of photovoltaic cells

由 图4（a），（b）可 知，随 着 太 阳 辐 射 强 度 的 变化，两类忆阻光伏电池模型的输出特性和实际模型的输出特性的变化规律保持一致。由图4（c），（d）可知，随着环境温度逐渐升高，光伏电池的开路电压（输出功率）均逐渐减小，且与I类忆阻光伏电池模型相比，II类忆阻光伏电池模型的输出特性对环境温度的变化更为敏感，更接近实际模型。

2.2 内部参数对忆阻光伏电池的影响

本文选择忆阻器的工艺参数作为研究对象，分别讨论各参数对两类忆阻光伏电池模型输出特性的影响。假设太阳辐射强度S为1 000 W/m2，环境温度T为25℃。

2.2.1工艺参数对忆阻光伏电池的影响

与一般的阻抗元件类似，忆阻器的阻抗特性受到自身长度、横截面积和电导率的影响。基于忆阻器的物理模型、电阻定律和式（4）得到，当忆阻器长度和横截面积分别存在偏差时，该忆阻器的 实 际 忆 阻 值M′（x，D），M′（x，SA）分 别 为[17]

式中：ρon，ρoff分别为忆阻器掺杂区域和非掺杂区域的电阻率；D0，SA0分别为理想状态下，忆阻器的长度和横截面积；λD为长度偏差因子；λSA为横截面积偏差因子。

λD，λSA的 计 算 式 分 别 为

基 于 式（8），（9），当 忆 阻 器 长 度 存 在 偏 差 时，两类忆阻光伏电池的伏安特性方程分别为

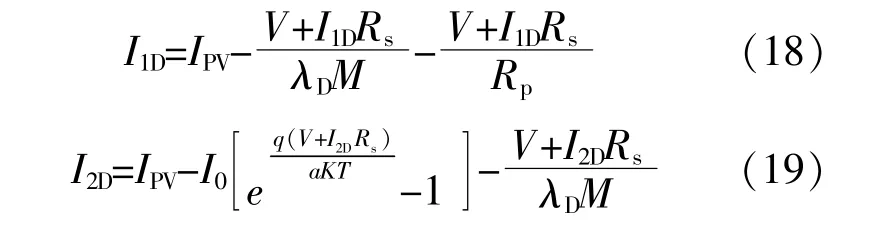
式 中：I1D，I2D分 别 为 忆 阻 器 长 度 存 在 偏 差 时，I，II类忆阻光伏电池模型中流经串联电阻Rs的电流。

同理，当忆阻器横截面积存在偏差时，基于式（14），（15）得 到，两 类 忆 阻 光 伏 电 池 的 伏 安 特 性 方程分别为

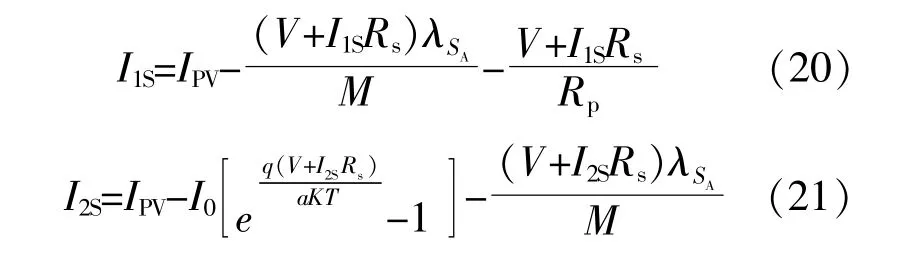
式中：I1S，I2S分别为忆阻器横截面积存在偏差时，I，II类忆阻光伏电池模型中流经串联电阻Rs的电流。

本文通过Matlab软件模拟了当工艺参数偏差不同时，忆阻器和忆阻光伏电池的电气特性。横截面偏差和长度偏差对忆阻值的影响见图5。

由图5可知，当忆阻器的横截面积或长度存在偏差时，忆阻器的阻值也随之发生变化（与理想情况下阻值不同）。即当忆阻器存在横截面偏差且偏差因子 λSA＜1时，该忆阻器的阻值大于理想状态下的阻值；同样地，当忆阻器存在长度偏差且偏差因子 λD＞1时，该忆阻器的阻值也会大于理想状态下的阻值。

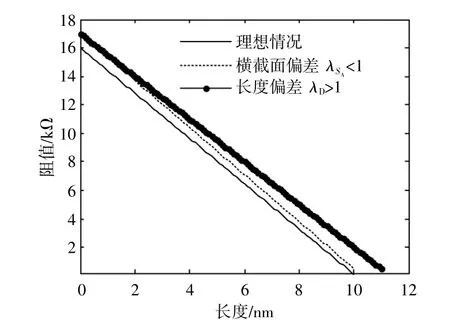
图5 横截面偏差和长度偏差对忆阻值的影响Fig.5 Effect of cross section and length variation on memristances

本文运用了蒙特卡洛算法[14]研究忆阻器的长度对两类忆阻光伏电池模型伏安特性的影响。图6为当忆阻器长度偏差为0.5时，两类忆阻光伏电池的伏安特性随忆阻器长度的变化情况。

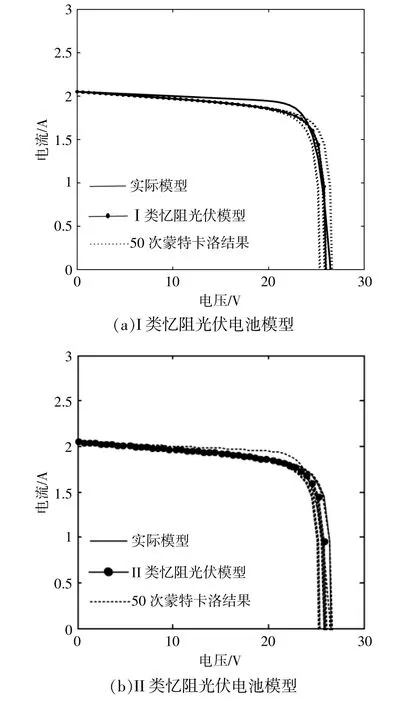
图6 当忆阻器长度偏差为0.5时两类忆阻光伏电池的伏安特性随忆阻器长度的变化情况Fig.6 Volt-ampere characteristics of two memristive photovoltaic cells when the length variation of memristor is 0.5

由图6可知，当忆阻器长度不存在偏差时，I，II类忆阻光伏电池模型的伏安特性曲线与实际模型的伏安特性曲线十分接近，但是尚未完全拟合；当忆阻器长度偏差为0.5，且算法运行50次时，发现两类忆阻光伏电池模型的动态伏安特性曲线均处于实际模型动态伏安特性曲线的两侧，且随着偏差的增大，能够进一步实现对实际模型动态伏安特性曲线的完全覆盖，这说明本文提出的两类忆阻光伏电池模型具有与实际电池模型相似的电气特性。

当忆阻器横截面偏差不同时，两种忆阻光伏电池的伏安特性如图7所示。

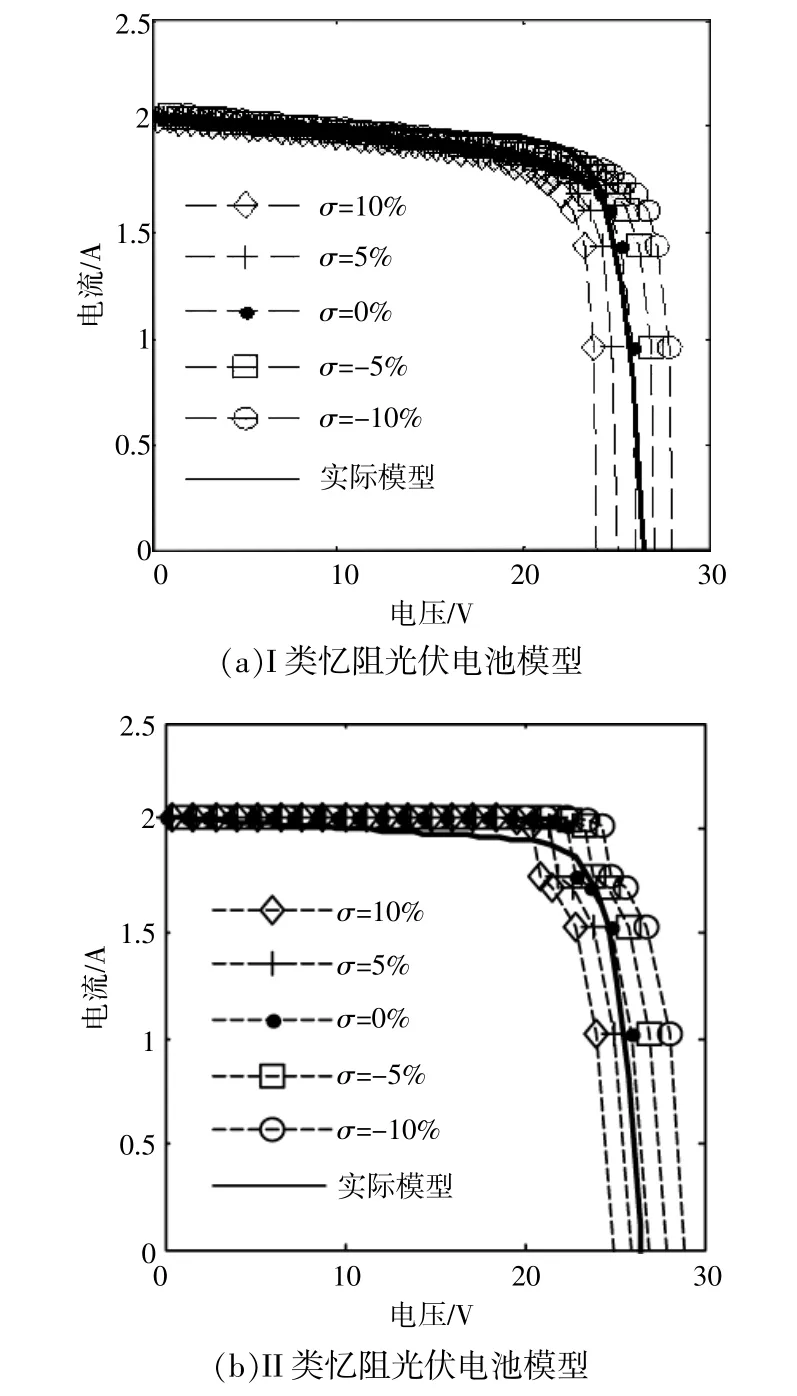
图7 当忆阻器横截面偏差不同时，两类忆阻光伏电池的伏安特性Fig.7 Volt-ampere characteristics of two memristive photovoltaic cells under different cross section variances

由图7可知，当忆阻器的横截面不存在偏差时（偏差 σ=0），两类忆阻光伏电池的伏安特性曲线与实际模型的伏安特性曲线十分接近，但是尚未完全拟合。改变忆阻器的横截面偏差，研究不同偏差情况下，两类忆阻光伏电池的伏安特性。当忆阻器横截面偏差σ分别为-10%，-5%，5%和10%时，两类忆阻光伏电池的伏安特性曲线分布在实际模型的伏安特性曲线两侧，说明忆阻器横截面的偏差能够使得忆阻光伏电池模型与实际模型的伏安特性存在完全拟合的可能性。当偏差σ为正值时（5%，10%），两类忆阻光伏电池的开路电压均减少，表明增大忆阻器横截面积能够减小光伏电池的开路电压；反之，当偏差 σ为负值时（-10%，-5%），两类忆阻光伏电池的开路电压均增加，表明减小忆阻器横截面积能够增大光伏电池的开路电压。

2.2.2忆阻器初始阻值对忆阻光伏电池的影响

设定忆阻器初始阻值M0分别为13.615，10.435，7.255，4.075 kΩ，研 究 忆 阻 器 初 始 阻 值 对忆阻光伏电池输出特性的影响。图8，9均为仿真结果。

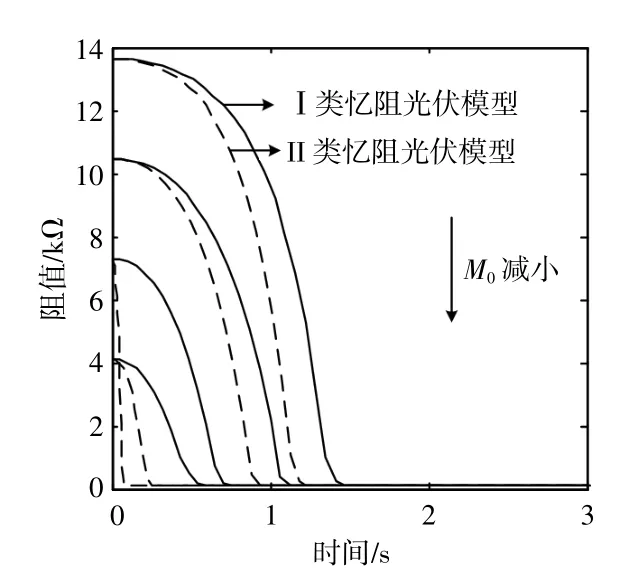
图8 当忆阻器初始阻值不同时，两类忆阻光伏电池模型中忆阻值随时间的变化曲线Fig.8 Memristance-time variation curves of two memristive photovoltaic cells under different initial memristor values

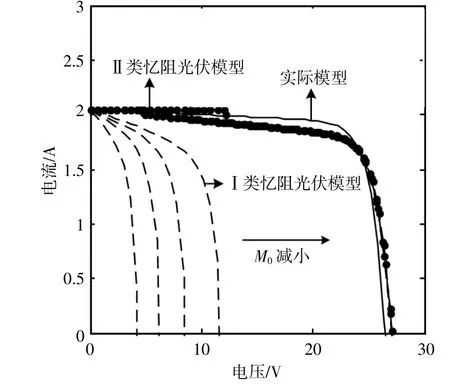
图9 当忆阻器初始阻值不同时，两类忆阻光伏电池模型的伏安特性Fig.9 Volt-ampere characteristics of two memristive photovoltaic cells under different initial memristor values

由图8可知，当忆阻器以正极性接入两类忆阻光伏电池模型中时，忆阻器的阻值将随着时间的增加逐渐减小，最终收敛于极小忆阻值；反之，当忆阻器以负极性接入两类忆阻光伏电池模型中时，根据忆阻器自身的阻值变化特点，可以合理地推测出：忆阻器的阻值将随着时间的增加逐渐增大，最终收敛于极大忆阻值。

由图9可知，相比于II类忆阻光伏电池模型，I类忆阻光伏电池模型的伏安特性与光伏电池实际模型的伏安特性更为接近。特别地，随着忆阻器初始阻值的增加，I类忆阻光伏电池模型的开路电压逐渐增加，而II类忆阻光伏电池模型的开路电压受到忆阻器初始阻值的影响较小，几乎不发生改变。

2.2.3极性参数对忆阻光伏电池的影响

忆阻器作为一种具有极性的二端电路元器件，当输入激励方向固定时，极性参数会影响忆阻值的变化方向[17]，从而间接影响忆阻光伏电池的电气特性。

图10为当忆阻器极性参数不同时，两类忆阻光伏电池模型中忆阻值随时间的变化曲线。

图10 当忆阻器极性参数不同时，两类忆阻光伏电池模型中忆阻值随时间的变化曲线Fig.10 Memristance-time variation curves of two memristive photovoltaic cells under different memristor polarity parameters

由图10可知：当忆阻器以负极性接入两类忆阻光伏电池模型中时（即η=-1），忆阻值均呈现逐渐增大的变化趋势；反之，当忆阻器以正极性接入两类忆阻光伏电池模型中时（即η=+1），忆阻值的变化则呈现完全相反的趋势，即逐渐减小，最终收敛于极小忆阻值。

图11为当忆阻器极性参数不同时两类忆阻光伏电池模型的伏安特性

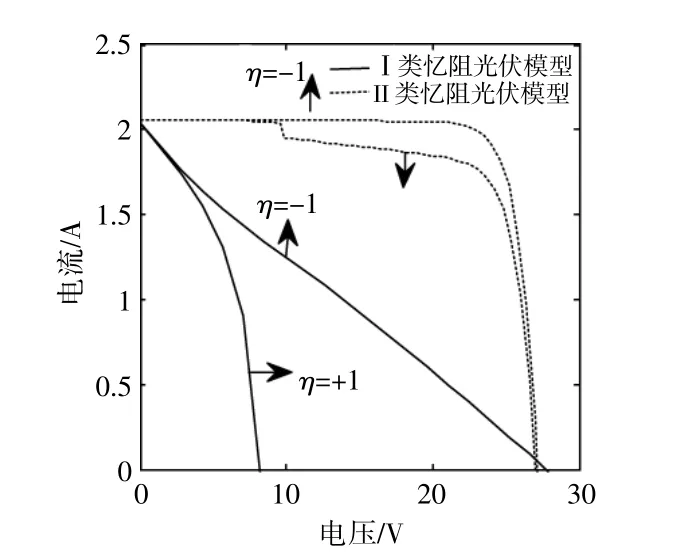
图11 当忆阻器极性参数不同时，两类忆阻光伏电池模型的伏安特性Fig.11 Volt-ampere characteristics of two memristive photovoltaic cells under different memristor polarity parameters

由图11可知，极性参数的变化更容易影响I类忆阻光伏电池模型的开路电压值。当忆阻器以负极性接入I类忆阻光伏电池模型时（η=-1），得到开路电压约为28.3 V；反之，当忆阻器以正极性接入I类忆阻光伏电池模型中时（η=1），得到的开路电压约为9.1 V。相比于I类忆阻光伏电池模型，极性参数的变化对II类忆阻光伏电池模型的开路电压影响较小。当极性参数发生变化时，II类忆阻光伏电池模型的开路电压均约为27.1 V。基于此，忆阻器作为一种纳米级电路元器件，当其与光伏电池模型结合时，若对应的等效电路制备完成，则其内部参数长度D、横截面积SA以及极性参数 η均不会发生改变。此时，通过不断地修正电路模型中忆阻器的初始值M0，使提出的两类忆阻光伏电池模型与传统光伏电池的V-I曲线尽可能重合，从而增加两类忆阻光伏电池模型的准确性和普适性。

本文通过修正初始阻值M0，得到5种不同的光伏电池模型之间的伏安特性绝对误差，如表1所示。

表1 5种不同光伏电池模型伏安特性的绝对误差Table 1 Absolute error of volt-ampere characteristics of five different photovoltaic cells %

为了使本文提出的I，II类忆阻光伏电池模型和其他3类电池模型的伏安特性计算误差均尽可能小，本文选择了较理想的忆阻器初始阻值：I类忆阻光伏电池模型的初始阻值M0设为15.75 kΩ；II类忆阻光伏电池模型的初始阻值M0为5.27 kΩ。

3 结论

针对传统光伏电池仿真模型存在的自适应性差、普适性弱的问题，本文基于光伏电池基本电路模型，分别运用非线性忆阻器代替光伏电池基本电路模型中的二极管和并联电阻，建立了两类忆阻光伏电池模型，并利用数值仿真结果验证了这两类忆阻光伏电池模型的有效性，得到如下分析结果。

①当外部参数发生变化时，提出的两类忆阻光伏电池模型的输出特性和实际模型的输出特性的变化规律保持一致。

②本文提出的两类忆阻光伏电池模型具有与实际电池模型相似的电气特性。