基于GA-BP神经网络的土壤-空气换热器换热量预测分析
董江涛,杜震宇
(太原理工大学 土木工程学院,山西 太原 030024)
0 引言
日光温室是我国应用比较广泛的设施农业建筑形式之一。日光温室内温度过高或过低都会严重影响农作物的品质和产量,而调节日光温室热湿环境须要消耗巨大的能源[1]。浅层地热能是一种分布比较广泛的可再生能源,且具有无污染、储量丰富的优点。土壤-空气换热器是一种利用浅层地热能的节能装置,该换热器不仅可以在冬季对换热管内的空气进行加温,还可以在夏季对换热管内的空气进行降温[2]。文献[3],[4]通过分析发现,将土壤-空气换热器用于处理温室热湿环境,具有良好的使用效果和经济效益。
国内外学者对土壤-空气换热器的换热特性和经济性进行了大量研究。Ozgener O和Ozgener L对土耳其一个温室中的土壤-空气换热器进行了经济性分析发现,土壤-空气换热器系统的能量损失主要发生在风机和换热管处,制热时,土壤-空气换热器系统的平均COP为10.51;制冷时,土壤-空气换热器系统的平均COP为10.09[5],[6]。范毅通过建立数值模型,分析了换热管进风口空气流速不同时,土壤-空气换热器的换热性能变化规律,并得到当换热管进风口空气流速为5.5 m/s时,土壤-空气换热器的换热量和COP达到最大值[7]。Niu建立了一维稳态数学模型,并基于数值模拟结果拟合了用于预测土壤-空气换热器制冷量的二次回归方程[8]。陈红兵利用土壤水分迁移的一维土壤热湿传递数学模型,分析了土壤源热泵蓄热过程中土壤温度场、湿度场的变化规律[9]。Wang利用热响应面法,建立了土壤-空气换热器预测系统数学模型,得到换热管进风口空气与土壤温度之间的差值,分析了换热管直径、长度和换热管内空气流速这4个因素对土壤-空气换热器系统中换热管进、出风口空气温差和显热换热能力 的 影 响[10]。
本文对日光温室中土壤-空气换热器的换热性能进行试验研究,分析了土壤-空气换热器在不同运行工况下的换热性能,同时,基于GA-BP神经网络建立了土壤-空气换热器换热量的预测模型,该模型为设计、优化土壤-空气换热器提供依据。
1 试验简介
本文试验所用的日光温室位于太原市小店区,日光温室朝向为正南,长度为63 m,宽度为9.7 m;北墙高度为3.1 m,厚度为1.04 m;南墙高度为0.4 m,厚度为0.18 m;东、西墙厚度分别为1.0,0.65 m。北墙和东、西墙均为石灰浆砌实心黏土红砖,中间加有聚苯板保温层和空心层,空心层以炉渣和土填充,屋面覆盖塑料薄膜为聚乙烯流滴性PVC膜,该膜的最高点距离地面4.1 m。日光温室断面尺寸如图1所示。

图1 日光温室断面尺寸Fig.1 The cross-section dimensions of the solar greenhouse
土壤-空气换热器内的换热管共有2层,每层有8根换热管,换热管间水平间距为1 m,土壤-空气换热器管道布置图如图2所示。编号为1,2,3,4的 换 热 管 的 第 一 层 埋 深 均 为1 m,第 二 层埋深均为2 m,换热管管径均为110 mm;编号为5,6,7,8的 换 热 管 的 第 一 层 埋 深 均 为1 m,第 二 层埋深均为2 m,换热管管径均为90 mm。6号换热管第一层埋管为测试管。为了便于通过水泵将换热管内冷凝水集中排出,本文将换热管按i=0.01的坡度布置,西南角为最低点。
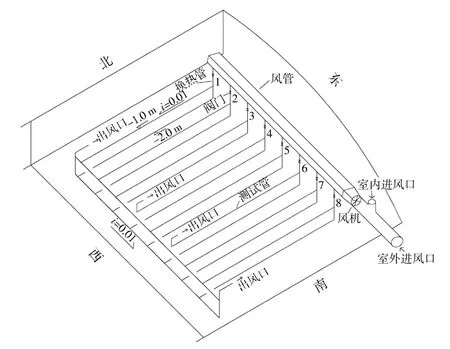
图2 土壤-空气换热器管道布置图Fig.2 Piping layout of earth-air heat exchanger
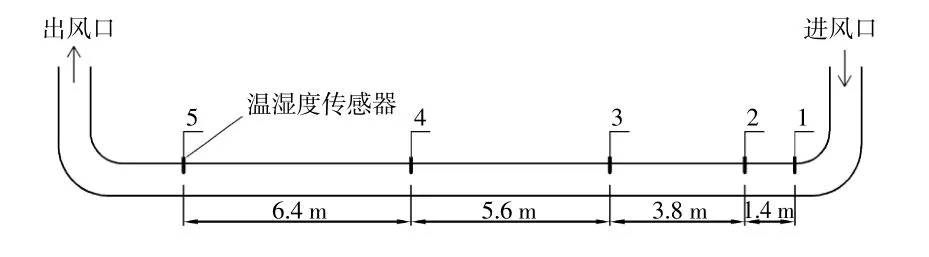
图3 换热管内传感器布置图Fig.3 Layout of sensors in tube
换热管内传感器布置图如图3所示。由图3可知,换热管内传感器的布置采用前密后疏的原则,依次在与换热管进风口之间的距离L分 别 为0,1.4,5.2,10.8,17.2 m处 布 置。本 文所用传感器为SLHT16空气温湿度传感器,该传感器具有小巧、抗干扰能力强的特点,测量温度为-40~85℃,精度为±0.3℃;测量相对湿度为0~100%,精度为±1.8%。试验数据通过采集模块和检测软件自动采集,并上传至电脑。
试验 时间为8月2-23日的8:00-18:00。白天开启风机,使土壤-空气换热器系统运行;晚上关闭风机,让土壤温度自然恢复。本文针对不同的换热管内空气流速、换热管长度和空气参数变化情况进行记录。本文选取8月6日(换热管内空气流速为2 m/s)、8月8日 (换热管内空气流速为4 m/s)、8月20日 (换 热管 内空 气流 速为6 m/s)3 d换热管内空气温度和湿度数据作为典型数据对土壤-空气换热器系统换热性能进行分析。上述测试日均为晴朗天气。
2 试验数据分析
2.1 换热管内空气温度和焓值分析
图4为换热管内空气流速和换热管长度不同时,换热管出风口空气温度随时间的变化情况。

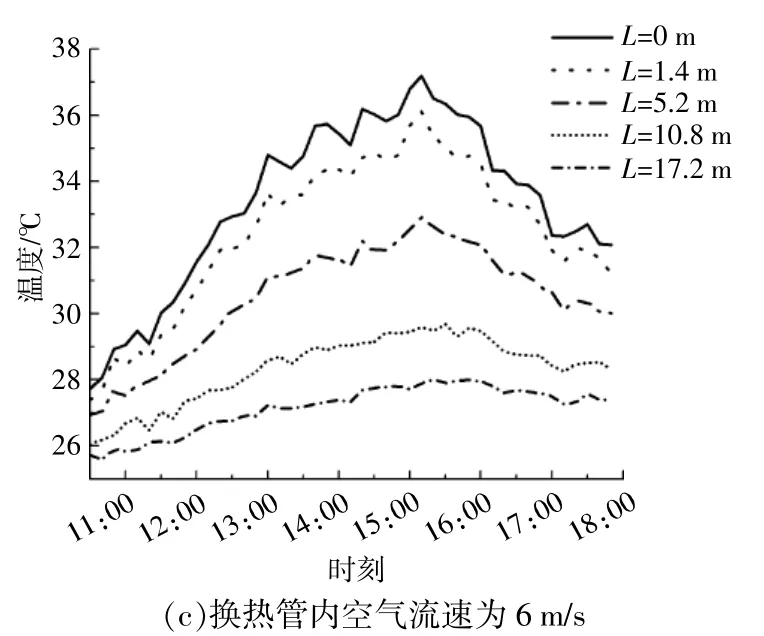
图4 换热管内空气流速和换热管长度不同时,换热管出风口空气温度随时间的变化情况Fig.4 The air temperature at the outlet of heat exchange tube changed with time under different air velocity and different length of heat exchange tube
由图4可知,换热管进风口(L=0)处,当换热管内空气流速分别为2,4,6 m/s时,换热管进风口 空 气 温 度 分 别 为30.3~36.5,30.8~36.4,27.7~37.2℃。在换热管长度为17.2 m的情况下,当换热管内空气流速分别为2,4,6 m/s时,换热管出风 口 空 气 温 度 分 别 为25.0~25.9,25.4~26.5,25.6~28.0℃。综上可知,在换热管长度不变的情况下,换热管内空气流速越小,换热管出风口空气温度越低,且波动幅度也越小;在换热管内空气流速不变的情况下,换热管长度越大,换热管出风口空气温度越低,且波动幅度也越小。
图5为运行期内,换热管内空气流速不同时,换热管内空气平均温降随换热管长度的变化情况。
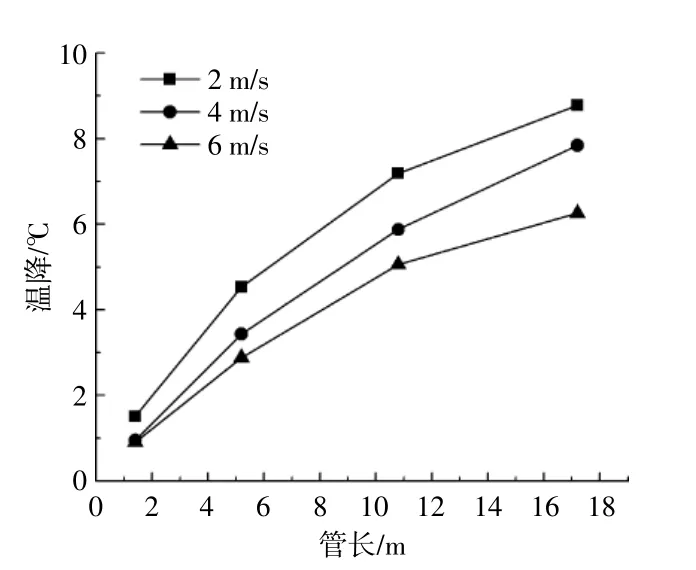
图5 运行期内,换热管内空气流速不同时,换热管内空气平均温降值随换热管长度的变化情况Fig.5 The average air temperature drop changed with the length of the heat exchange tube under different air velocity
由图5可知,在换热管前段,换热管内空气温度下降得较快,随着换热管长度不断增加,换热管内空气温降逐渐趋于平缓。当换热管内空气流速为2 m/s时,换热管内空气总温降为8.8℃,换热管前端1.4 m处,换热管单位长度空气温降为1.1℃,换热管末端6.4 m处,换热管单位长度空气温降仅为0.3℃;当换热管内空气流速为4 m/s时,换热管内空气总温降为7.8℃,换热管前端1.4 m处,换热管单位长度空气温降为0.7℃,换热管末端6.4 m处,换热管单位长度温降为0.3℃;当换热管内空气流速为6 m/s时,换热管内总温降为6.3℃,换热管前端1.4 m处,换热管单位长度空气温降为0.7℃,换热管末端6.4 m处,换热管单位长度空气温降为0.2℃。综上可知,换热管单位长度空气温降随着换热管长度的增加而下降;为了获得较大的空气温降,不断增加换热管长度是不经济的。
图6为运行期内,换热管内空气流速不同时,换热管内空气平均焓降随换热管长度的变化情况。
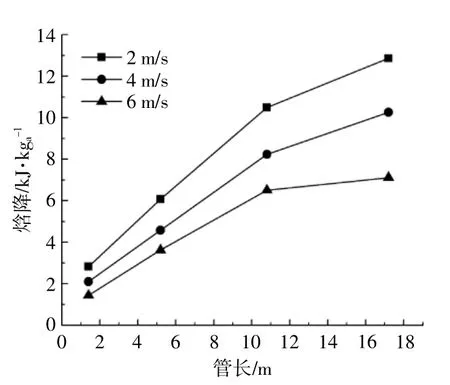
图6 运行期内,换热管内空气流速不同时,换热管内空气平均焓降值随换热管长度的变化情况Fig.6 The average air enthalpy drop changed with the length of the heat exchange tube under different air velocity
由图6可知,换热管内空气焓降和换热管内空气温降具有类似的规律,在换热管前段,随着换热管长度的增加,换热管内空气的焓降增加得较快。当换热管长度增加到一定值时,换热管内空气焓降的增加趋势趋于稳定。换热管末端6.4 m处,当换热管内空气流速分别为2,4,6 m/s时,换热管单位长度空气焓降(干空气)分别为0.37,0.32,0.096 kJ/kg。综上可知,换热管内空气流速越大,换热管长度对土壤-空气换热器的换热性能的影响越低。
2.2 土壤-空气换热器换热量分析
土壤-空气换热器显热换热量Qs的计算式为
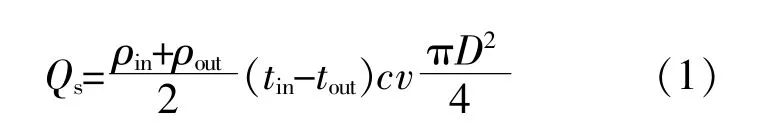
式 中:ρin为 换 热 管 进 风 口 空 气 密 度,kg/m3;ρout为换热管出风口空气密度,kg/m3;tin为换热管进风口空气温度,℃;tout为换热管出风口空气温度,℃;c为 空 气 比 热 容,J/(kg·℃);v为 换 热 管 内 空 气 流速,m/s;D为 换 热 管 管 径,m。
土壤-空气换热器全热换热量Qt的计算式为
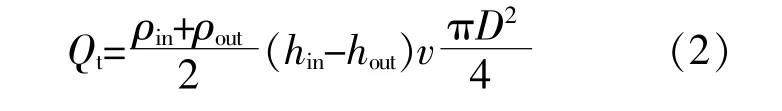
式中:hin为换热管进风口空气焓值,kJ/kg;hout为换热管出风口空气焓值,kJ/kg。
图7为运行期内,换热管内空气流速不同时,换热管平均换热量随换热管长度的变化情况。
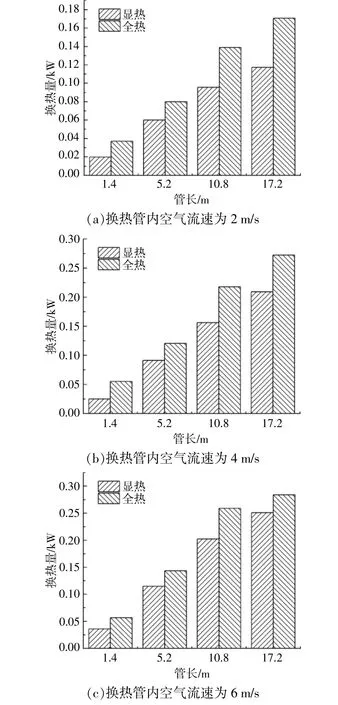
图7 运行期内,换热管内空气流速不同时,换热管平均换热量随换热管长度的变化情况Fig.7 The average heat exchange quantity changed with the length of the heat exchange tube under different air velocity
由图7可知,当换热管长度为1.4 m,换热管内空气流速分别为2,4,6 m/s时,土壤-空气换热器显热换热量在全热换热量中的占比分别为53.68%,45.08%,63.51%;当换热管长度为10.8 m,换热管内空气流速分别为2,4,6 m/s时,土壤-空气换热器显热换热量在全热换热量中的占比分别为68.89%,71.70%,78.13%;当换热管长度为17.2 m,换热管内空气流速分别为2,4,6 m/s时,土壤-空气换热器显热换热量在全热换热量中的占比分别为68.63%,76.83%,88.37%。
由图7还可以看出,在换热管长度为17.2 m的情况下,当换热管内空气流速为6 m/s时,土壤-空气换热器全热换热量较大,为283.94 W;当换热管内空气流速为4 m/s时,土壤-空气换热器全热换热量为272.39 W;换热管内空气流速为2 m/s时,土壤-空气换热器全热换热量较小,为170.79 W。
综上可知,随着换热管内空气流速增大,土壤-空气换热器全热换热量逐渐增大。这是由于换热管内空气流速越大,传热系数越大,可同时处理的空气更多,因此,换热量也随之增大。此外,随着换热管内空气流速增大,空气在换热管内换热时间减少,空气温降变小,减弱了传热效果,导致土壤-空气换热器全热换热量增幅趋于稳定。因此,当换热管内空气流速为6 m/s时,土壤-空气换热器全热换热量仅比流速为4 m/s时增加了4.24%。
3 GA-BP神经网络模型
3.1 BP神经网络
BP(Back Propagation)神经网络是一种采用误差反向传播算法进行学习的多层前馈网络,该网络可以实现复杂的非线性映射函数,计算结果具有较高的精度。与其他预测方法相比,BP神经网络具有简单易行、对数据有较高容错性等特点,因此,是目前使用频率较多且技术较成熟的神经网 络 模 型 之 一[11],[12]。
BP神经网络的拓扑结构包括输入层、隐含层和输出层。输入层和输出层的节点数由输入、输出变量的维数决定;隐含层节点数根据经验公式和试凑法确定。经验公式为

式中:y为隐含层节点数;m为输入层节点数;n为输 出 层 节 点 数;a为 常 数,取1~10[13]。
隐含层的层数和节点数对BP网络的性能有很大影响,一个隐含层可以逼近任意的映射关系。
3.2 遗传算法优化
虽然BP神经网络应用范围广泛,但其仍存在一些缺陷:①学习效率低,收敛速度慢;②在训练过程中,网络随机生成的初始权值和阈值容易使网络陷入局部最优。遗传算法(Genetic Algorithm,GA)通过模拟生物进化中的遗传过程,可以有效解决优化问题。遗传算法通过选择、交叉和变异对种群的个体进行筛选,留下适应度较高的个体,剔除适应度较差的个体,不断进行进化迭代,直至得到满足条件的个体为止[14]。利用遗传算法对BP神经网络的初始权值和阈值进行优化,可以避免网络陷入局部最优,提高训练速度。具体优化步骤如下[15]。
①种群初始化。设定种群个体数,个体编码方式选择实数编码。每个个体由一个包含了BP神经网络全部权值和阀值的实数串组成。
治愈:治疗后2天内排便次数在1次以上,便质明显转润,排便非常通畅,短期内症状没有再次复发。有效:治疗后患者3天以内患者已经排便,便质开始转润,排便尚通畅。无效:便秘症状无改善。总有效率=(治愈+有效)/总观察例数×100%。
②设定适应度函数F。F的计算式为
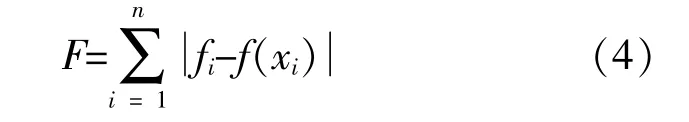
式 中:fi为 期 望 输 出 值;f(xi)为 预 测 输 出 值。
适应度函数值越小,预测结果越精准,该个体被保留下来的机会越大。
③选择操作。计算每个个体的适应度函数值,采用轮盘赌法选择优秀个体组成新的种群。
④交叉操作。设定交叉概率Pc为0.5,随机选择个体进行交叉操作,选中2个配对个体互换其中的部分基因,产生2个新的个体,即个体ak,al在第j位基因进行交叉产生新基因akj,alj。
akj,alj的 操 作 表 达 式 为
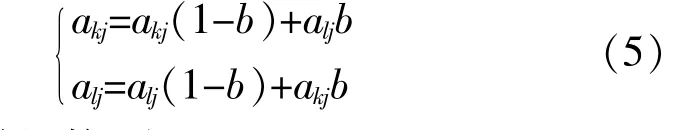
式 中:b为 随 机 数,取0~1。
⑤变异操作。设定以变异率pm为0.04,随机选择个体进行变异操作,选中的个体ai在第j个基因进行变异,得到新基因aij。
aij的操作表达式为

式 中:amax,amin分 别 为 基 因aij的 上、下 界;r2为 一 个随机数;g为当前进化次数;Gmax为最大进化次数;r为 随 机 数,取0~1。
⑥计算新产生的种群中个体的适应度函数值,若适应度函数值达到要求或进化次数达到最大值,则进化停止,否则返回步骤③。
⑦通过遗传算法优化得到的个体实数串赋予BP网络初始权值和阀值。
4 仿真预测分析
4.1 建立模型
为了了解遗传算法对BP神经网络的优化效果,本文分别基于BP神经网络和GA-BP神经网络建立了土壤-空气换热器换热量的预测模型。该模型以换热管进风口空气的温度、相对湿度、换热管长度和换热管内空气流速作为输入变量,以土壤-空气换热器全热换热量作为输出变量,网络结构采用4-8-1结构,学习函数采用learngdm函数,训练函数采用Levenberg-Marquardt算法的trainlm函数,隐含层节点转移函数采用tansig函数,输出层节点转移函数采用purelin函数,学习速率设为0.01,最大迭代次数设为100。
在遗传算法的优化过程中,各参数对最终预测结果有着重要影响,因此,须要将各参数取值设置在合理的范围内,以达到理想的优化效果。遗传算法各参数设置为种群规模为50,进化次数为20,交 叉率 为0.5,变 异率 为0.04。
本文将得到的试验数据分为训练样本和测试样本,随机抽取70%的试验数据组成训练样本,另外30%的试验数据组成测试样本。为了避免因各数据之间不同量纲对预测结果造成影响,本文对输入变量和输出变量进行归一化处理,将输入、输出变量映射到[0,1]内,训练结束后,再将得到的预测输出值进行反归一化处理,即可得到实际预测输出值。
4.2 预测结果及误差分析
图8,9分别为基于BP神经网络和GA-BP神经网络建立的土壤-空气换热器换热量的预测结果。
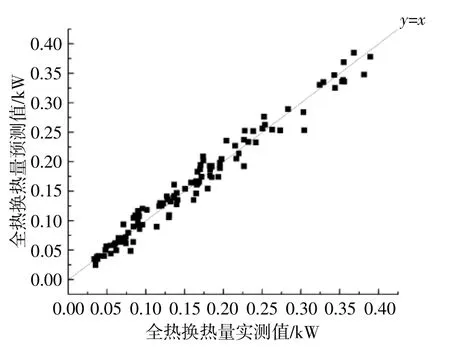
图8 基于BP神经网络建立的土壤-空气换热器换热量的预测结果Fig.8 The prediction model of earth-air heat exchanger heat exchange quantity based on BP neural network
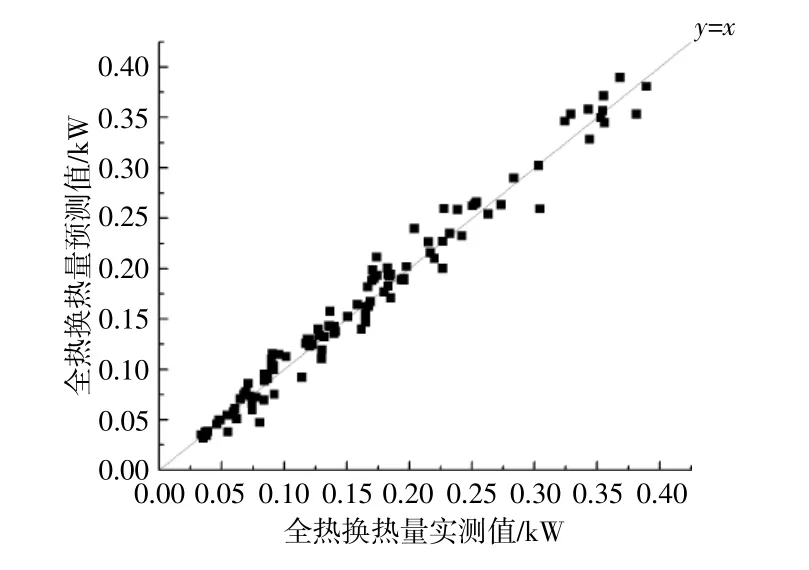
图9 基于GA-BP神经网络建立的土壤-空气换热器换热量的预测结果Fig.9 The prediction model of earth-air heat exchanger heat exchange quantity based on GA-BP neural network
由图8,9可知,这2个模型均具有良好的预测效果,预测值接近实测值,且二者具有良好的线性相关性。
本文选择平均相对误差MRE、均方根误差RMSE和平方相关系数r2作为基于BP神经网络和GA-BP神经网络的土壤-空气换热器换热量预测模型(以下简称为基于BP神经网络和GABP神经网络的换热量预测模型)的评价指标,验证遗传算法对BP神经网络优化的有效性。r2表征预测值与实测值之间的线性相关关系,r2的值越接近1,表明预测值与实测值之间的线性相关性越强。
MRE,RMSE,r2的 计 算 式 分 别 为
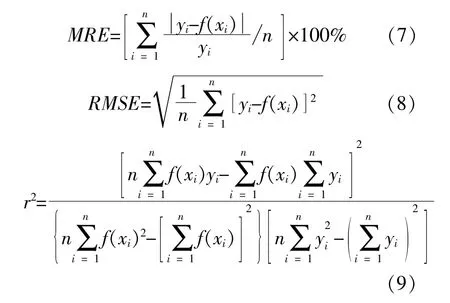
式中:yi为实际样本输出值。
基于BP神经网络和GA-BP神经网络的换热量预测模型模拟结果的MRE,RMSE,r2如表3所示。

表3 基于BP神经网络和GA-BP神经网络的换热量预测模型模拟结果的MRE,RMSE,r2Table 3 Error comparison between BP neural network and GA-BP neural network
由表3可知,与基于BP神经网络的换热量预测模型相比,基于GA-BP神经网络的换热量预测模型的平均相对误差和均方根误差较小,r2更接近于1,预测值与实测值之间的线性相关性更强,所需的迭代次数更少,迭代速度更快。
5 结论
①在日光温室内,土壤-空气换热器的潜热换热量不应被忽视,应采用土壤-空气换热器全热换热量综合考量土壤-空气换热器的换热性能。
②换热管内空气流速一定时,随着换热管长度的增加,土壤-空气换热器的换热量的增加趋势逐渐下降。当换热管内空气流速分别为2,4和6 m/s时,若换热管长度从10.8 m增加到17.2m,则换热管末端6.4 m处,换热管单位长度空气焓降 分 别 为0.37,0.32,0.096 kJ/kg。
③换热管内空气流速与土壤-空气换热器换热量呈正相关,当换热管内空气流速逐渐增大时,土壤-空气换热器全热换热量的增量逐渐减小。相比于比换热管长度为17.2 m,换热管内空气流速为4 m/s的工况,当换热管长度为17.2 m,换热管内空气流速为6 m/s时,土壤-空气换热器全热换热量仅增加了4.24%。
④基于BP神经网络和GA-BP神经网络的换热量预测模型均能够对土壤-空气换热器换热量进行预测。
⑤基于GA-BP神经网络的换热量预测模型计算结果的平均相对误差为0.079 7,预测结果精度优于基于BP神经网络的换热量预测模型。

