空间曲梁单元的扭转修正系数研究
宋泰宇,李国平
(1.同济大学建筑设计研究院(集团)有限公司,上海 200092; 2.同济大学 土木工程学院,上海 200092)
1 引 言
有限单元法是在当今技术科学发展和工程分析中最强有力的数值方法[1,2],广泛应用于机械、桥梁和房屋等工程分析中。梁-杆件是工程结构的重要组成,有限元分析一般通过引入平截面假设将杆件简化为一维问题,从而采用梁单元求解。在实际工程中,常会采用曲线形梁结构,如桥梁工程中的弯梁和房屋工程中支撑球形网壳的曲梁等。由于曲梁的轴线是曲线,所以梁中的拉压、弯曲和扭转是耦合的,梁内存在扭矩。
有限元分析曲梁主要有两类单元,(1) 可以考虑扭矩的空间直梁单元; (2) 由三维实体单元退化而来的空间曲梁单元。空间直梁单元是用折线代替曲线,优点是表达格式较为简单,但是,直梁单元中的拉压、弯曲和扭转各自独立,互不耦合,因此使用直梁单元模拟的曲梁在离散时较为困难,会出现弯矩和扭矩不连续等问题,同时划分必须用较密集的网格;三维空间曲梁单元中的拉压、弯曲、扭转几种变形和应力状态是相互耦合的,这类单元的有限元程式是由三维实体单元推导而来,其位移和转动自由度相互独立,因此形函数只需要C0连续性[1],可以适用于各种形状的直、曲梁结构。同时,这类单元构造时考虑了横向剪切变形,可以同时适用于浅梁和深梁的分析。因此,当考虑计算的精确度和有限元程序的普遍适用性时,宜采用空间曲梁单元进行曲梁结构的分析。
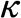
2 空间曲梁单元的剪应力
2.1 有限元程式

三维曲梁单元中任一点在全局坐标系中的几何位置为
(1)
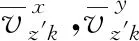
在小转动的条件下,空间曲梁单元中任一点在全局坐标系的位移场为
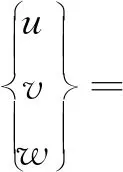
(2)
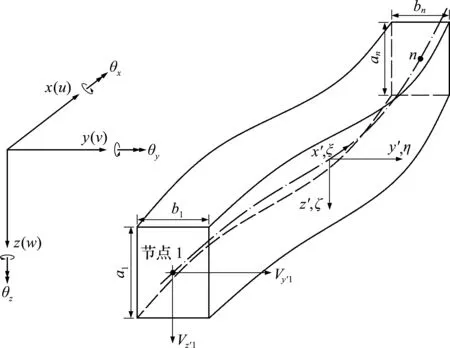
图1 三维空间曲梁单元[1]
式中{δk}={uk,vk,wk,θx k,θy k,θz k}T为结点k在全局坐标系下的结点位移向量,{uk,vk,wk}T为平动向量,{θx k,θy k,θz k}T为转动向量;其余符号意义同前。在局部坐标系中,三维空间曲梁单元的弹性本构矩阵的表达式为
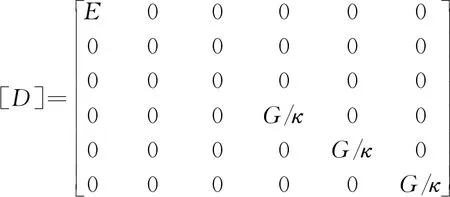
(3)
式中E和G分别为杨氏弹性模量和剪切刚度,κ为剪切校正因子。本文只列出与本文相关的方程,空间曲梁单元的完整有限元程式可参见文献[14]。空间曲梁单元在梁轴线是直线时退化为 Timo -shenko 梁单元。
本有限元程式中,数值计算采用减缩积分的3结点二次曲梁单元(2个高斯积分点),可有效避免剪切锁死和零能模式。
2.2 计算剪应力和真实剪应力
矩形截面梁发生扭转时,各截面发生翘曲,不再保持平面。但是,从式(2)可以看出,扭转角θx对轴向变形u没有影响,即空间曲梁单元不能考虑扭转翘曲的影响。根据理论和试验结果[15,16],对于跨长大于横截面尺寸4倍的实心截面梁来说,翘曲正应力和翘曲剪应力与相应的弯曲正应力和刚性扭转剪应力相比较小,一般不超过5%,可不考虑翘曲的影响,采用单纯扭转理论分析[15]。因此,空间曲梁单元不考虑翘曲影响所引起的误差较小,在工程设计容许范围内。
将式(2)的位移场代入弹性力学的基本几何方程,即可得到空间曲梁单元的6个应变分量,将剪应变代入式(3)即可得剪应力,矩形截面空间曲梁单元上由横向弯曲和扭转产生的剪应力分别如 图2(a,c)所示。可以看出,计算的弯曲剪应力沿截面高度方向为常值,而真实的弯曲剪应力近似为抛物线分布(图2(b));计算的扭转剪应力呈线性分布,在对角线顶点处达到最大值,而真实扭转剪应力呈非线性分布,在矩形长边中点达到最大值,在对角线顶点处为0(图2(d))。
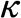
3 扭转修正系数

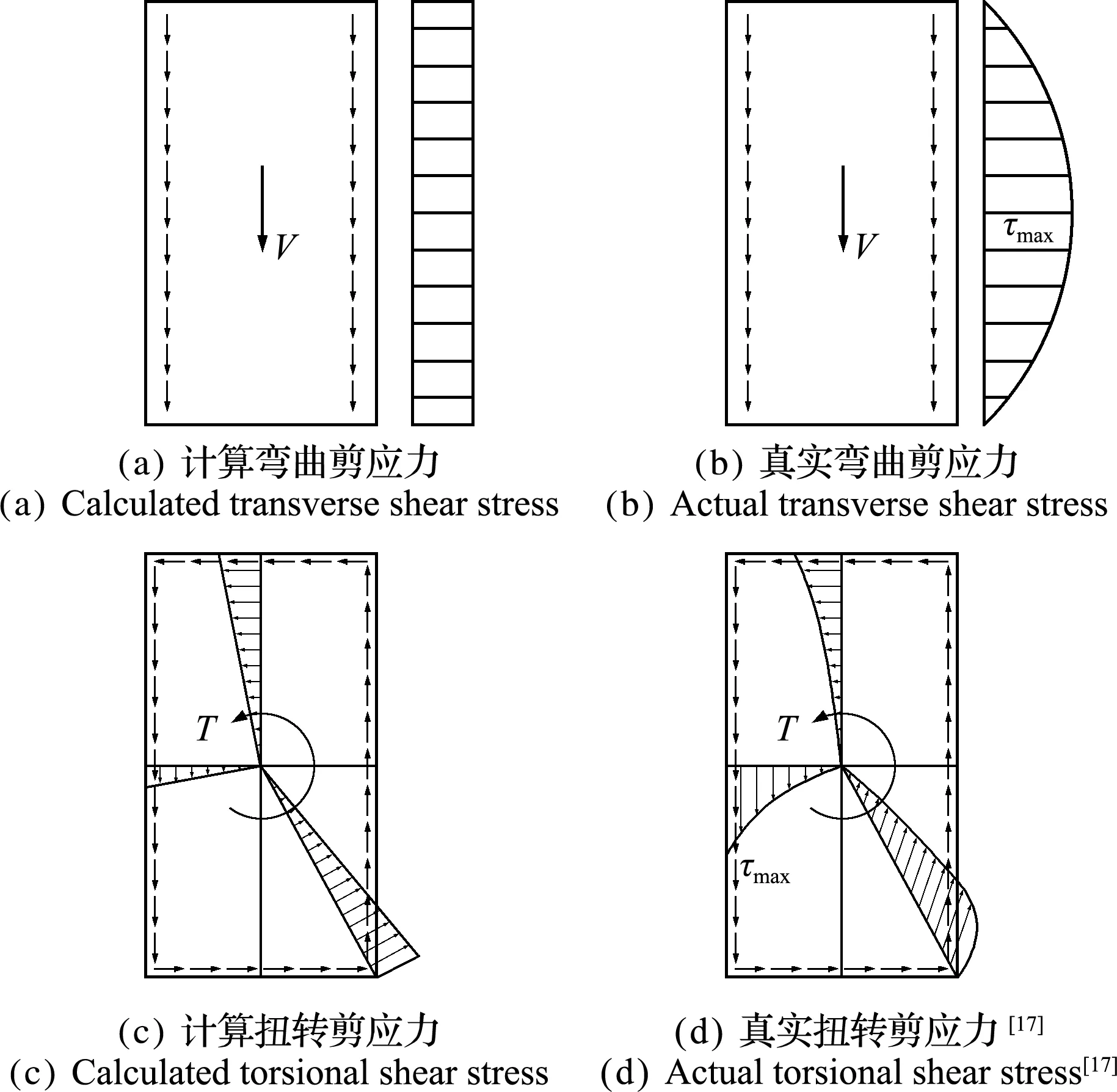
图2 梁单元截面上的剪应力分布
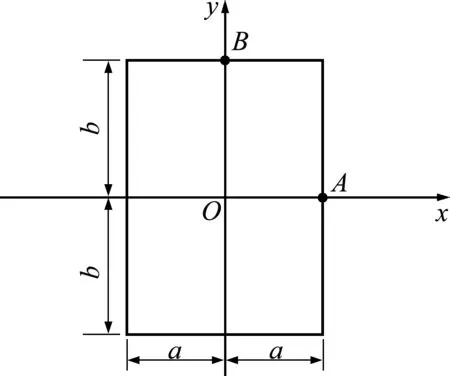
图3 梁截面
利用弹性力学的应力函数可得到截面上扭转剪应力的解析解[18]为
(4)
(5)
式中αn=(2n+1)π/2a(n=0,1,2,…)。根据式(2)和几何方程可得空间曲梁单元截面上的剪应力
τx z 2=-θGy,τz y 2=θGx
(6,7)
(8)
(9)


4 算例验证分析
基于上述的空间曲梁单元模型,文献[14]编制了相应的有限元电算程序。为了验证上述推导的扭转修正系数的正确性,以一矩形截面曲线悬臂梁为例,基于实体单元模型的结果对空间曲梁单元模型计算结果的正确性进行验证和分析。

表1 扭转刚度修正系数Tab.1 Correction factors of torsional stiffness )
曲线悬臂梁的平面布置如图4所示,选取两个截面尺寸分别为20cm(高)×20cm(宽)和20cm×10cm,E=3.45×107kN/m2,G=1.725×107kN/m2,在悬臂梁末端施加竖向单位力P =1kN。实体有限元模型利用有限元软件ABAQUS[19]建立,模型采用网格细化的三次高阶单元(C3D20R)以保证模型的计算准确度(图5)。
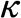
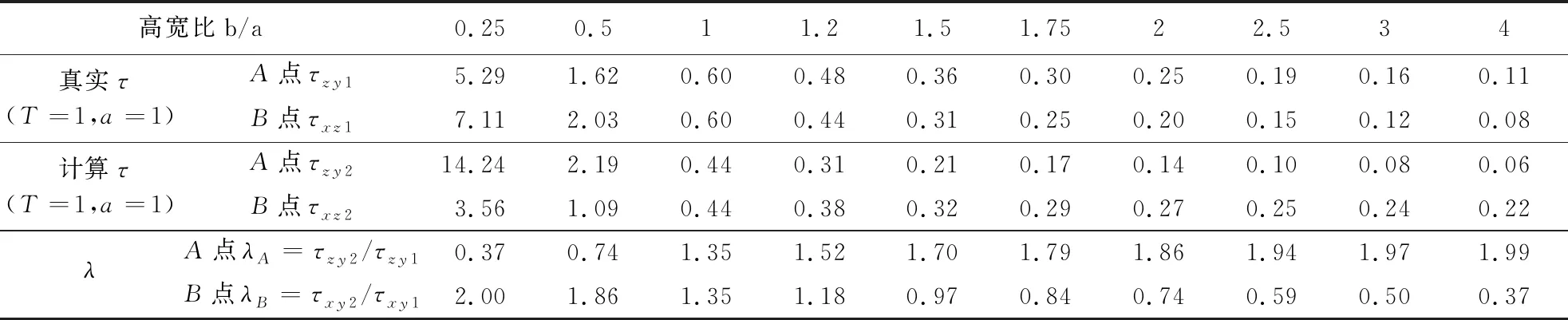
表2 扭转剪应力修正系数λTab.2 Correction factors of torsional shear (λ)
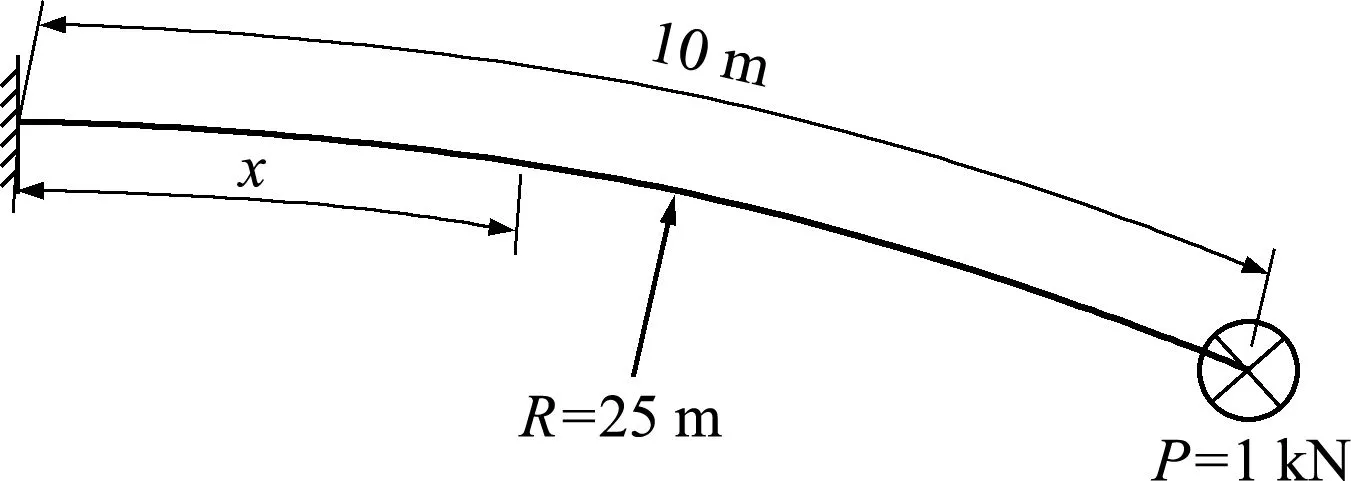
图4 曲线悬臂梁平面

图5 曲线悬臂梁的实体单元模型

图6 曲线悬臂梁沿梁长的挠度和扭转角的对比
5 结 论
(1) 曲梁是典型的空间结构,具有弯扭耦合特性,受力状态较复杂。对于曲梁结构的分析,与解析解法、实体单元模型和直梁单元模型相比,采用空间曲梁单元模型最符合曲梁真实的几何和受力特点,分析方法具有较高的准确度和效率。


(6) 与本文研究内容相关的,空间曲梁单元模型采用分层法进行非线性受力性能分析时,单元的分层数需不少于4层(减缩积分),每个单元对应的圆心角不大于6°,以保证获得准确的弯剪扭受力性能。
参考文献(References):
[1] 王勖成.有限单元法[M].北京:清华大学出版社,2003.(WANG Xu-cheng.FiniteElementMethod[M].Beijing:Tsinghua University Press,2003.(in Chinese))
[2] 朱伯芳.有限单元法原理与应用(第三版)[M].北京:中国水利水电出版社,2009.(ZHU Bo -fang.PrincipleandApplicationofFiniteElementMethod(3r dEdition) [M].Beijing:China Water & Power Press,2009.(in Chinese))
[3] Kwon Y W,Bang H.TheFiniteElementMethodUsingMATLAB [M].CRC Press,2000.
[4] 石志源.桥梁结构电算(第二版)[M].北京:人民交通出版社,2010.(SHI Zhi-yuna.ComputingforBridgeStructures(2n dEdition) [M].Beijing:China Communications Press,2010.(in Chinese))
[5] Cowper G R.The shear coefficient in Timoshenko’s beam theory[J].JournalofAppliedMechanics,1966,33(2):335-340.
[6] Whitney J M.The effect of transverse shear deformation on the bending of laminated plates[J].JournalofCompositeMaterials,1969,3(3),534-547.
[7] Shabana A A,Yakoub R Y.Three dimensional abso -lute nodal coordinate formulation for beam elements:Theory [J].JournalofMechanicalDesign,2001,123(4):606-613.
[8] Murín J,Aminbaghai M,Kutiš V,et al.A new 3D Timoshenko finite beam element including non-uniform torsion of open and closed cross sections [J].EngineeringStructures,2014,59:153-160.
[9] 张永信.计及弯扭耦合效应的空间梁杆结构计算分析方法[D].哈尔滨工业大学,2017.(ZHANG Yong-xin.The Calculation and Analysis Method of Spatial Beam Structure Considering Bending and Torsion Coupling Effect [D].Harbin Institute of Technology,2017.(in Chinese))
[10] 宋子康,蔡文安.材料力学[M].上海:同济大学出版社,2005.(SONG Zi-kang,CAI Wen-an.MechanicsofMaterials[M].Shanghai:Tongji University Press,2005.
[11] Ferguson G H,Clark R D.A variable thickness,curved beam and shell stiffening element with shear deformations [J].InternationalJournalforNumericalMethodsinEngineering,1979,14(4):581-592.
[12] 何 志,陈建芳,李 伟,等.考虑剪切变形的开口薄壁杆单元扭转刚度矩阵[J].广西大学学报(自然科学版),2013,38(4):795-800.(HE Zhi,CHEN Jian-fang,LI Wei,et al.Torsional stiffness matrix of open thin-walled beam element considering torsional shear deformation [J].JournalofGuangXiUniveristy(NaturalScienceEdition),2013,38(4):795-800.(in Chinese))
[13] 刘 建,陈 勇,曹 洲,等.基于一阶薄壁梁理论的开口截面剪应力不均匀系数的精确计算[J].工业建筑,2015,45(10):155-160.(LIU Jian,CHEN Yong,CAO Zhou,et al.Accurate calculation of the shear stress non-uniform coefficient on the open section based on the first-order thin-walled beam theory [J].IndustrialConstruction,2015,45(10):155-160.(in Chinese))
[14] 宋泰宇.混凝土曲线箱梁桥极限状态分析理论及方法 [D].同济大学,2019.(SONG Tai-yu.Analysis and Calculation Methods of Curved Reinforced and Prestressed Concrete Box-section Girder Bridges [D].Tongji University,2019.(in Chinese))
[15] 邵容光,夏 淦.混凝土弯梁桥[M].北京:人民交通出版社,1994.(SHAO Rong-guang,XIA Gan.CurvedConcreteGirderBridge[M].Beijing:China Communications Press,1994.(in Chinese))
[16] 孙光华.曲线桥梁计算[M].北京:人民交通出版社,1995.(SUN Guang-hua.CalculationsofCurvedBridges[M].Beijing:China Communications Press,1995.(in Chinese))
[17] 于海祥,武建华,李仁佩.对矩形截面杆弹性自由扭转的探讨[J].力学与实践,2007,29(2):73-74.(YU Hai-xiang,WU Jian-hua,LI Ren-pei.Discussions of elastic torsion in rectangular section beam [J].Me-chanicsinEngineering,2007,29(2):73-74.(in Chinese))
[18] 程昌钧.弹性力学[M].兰州:兰州大学出版社,1996.(CHENG Chang-jun.Elasticity[M].Lanzhou:Lanzhou University Press,1996.(in Chinese))
[19] SIMULIA.Abaqus User’s Manual 6.11 [S].Providence,RI,2011.

